基于改进矩阵束的动态同步相量测量算法
黄瑞 宋健 肖宇 刘谋海 温和



摘要:随着现代电网规模不断增大,分布式电源大规模接入,强谐波、高噪声和信号动态多变等问题会降低同步相量测量算法的准确度.为准确测量现代电网同步相量参数,提出一种结合二阶泰勒动态相量模型和改进矩阵束优势的同步相量测量算法,用于动态条件下电力系统同步相量幅值和相角参数精确测量.本文先对算法进行数学推导,然后根据我国同步相量装置检测规范中指定的实验案例对测量准确度进行详细评估.实验结果表明,算法在频率偏差、幅度调制等情景下具有很高的测量精度,符合我国同步相量检测规范要求,具有一定工程应用价值.
关键词:同步相量测量;动态相量模型;矩阵束;频率估计;最小二乘法
中图分类号:TM714
文献标志码:A
同步相量测量单元(phasor measurement unit,PMU)作为现代电网智能感知层的重要数据入口,在电网故障诊断、电压稳定性监视、低频振荡分析、暂态稳定性分析和控制等方面发挥着重要作用,高精确度和实时性的同步相量测量算法是保证PMU稳定高效工作的先决条件[1,2].随着现代电网规模的不断增大,配电网将面临如下变化,(1)以光伏发电为代表的分布式电源大规模接入,可能导致配电网电压和功率的振荡;(2)电动汽车的大规模无序充电,可能致使配电网电压跌落;(3)电动汽车和分布式电源大规模应用,可能造成配电网谐波含量上升.这些改变使配电网中的PMU面临着强谐波、强噪声和测量信号动态多变等环境,使得同步相量测量算法的设计面临巨大挑战[3-5].
为了应对配电网全新测量环境的挑战,国内外学者提出了很多改进型或者全新的PMU测量算法.根据基本原理,主要分为两类:1)基于离散傅立叶变换(Discrete Fourier Transform,DFT)的算法,如文献[6-8]等针对同步相量和频率测量误差与滤波器频响特性的关系,根据最优设计准则,构建DFT类算法的等效数字滤波器组,提高了DFT类动态同步相量测量算法的抗谐波能力.文献[9]将泰勒相量模型分解为基本分量和若干子分量,然后用DFT分别求出各分量,最后进行合成与修正,减轻了功率振荡对测量精度的影响.文献[10]研究了DFT在非同步采样条件下的相角误差分布规律后,用相角差对被测频率跟踪测量,得到精度较高的频率值.文献[11]提出了一种基于频率偏移的DFT修正方法,能实现动态变化过程的相量测量.尽管基于DFT的算法具有很强的抗谐波能力和较高的计算效率,但由于频谱泄漏的影响,此类算法在间谐波或带外干扰存在时性能较差.2)基于泰勒动态相量模型和最小二乘法的算法,文献[12]引入强跟踪卡尔曼滤波器,由理论残差与实际残差的失配情况来调整测量过程,增强对动态信号的跟踪能力.文献[13]提出了泰勒加权最小二乘算法(Taylor Weighted Least squares,TWLS),其实质是采用窗函数抑制旁瓣干扰和带外噪声.文献[14]将加权最小二乘算法中的泰勒多项式替换为通带波纹更低且阻带衰减更高的Sinc插值多项式,提高了此类算法在频偏、谐波振荡和线性调频条件下的测量精度,但是间谐波干扰对算法精确度的影响很大.
综合上述背景,为提高泰勒动态相量模型类算法的抗谐波与频偏干扰性能,本文提出一种结合改进矩阵束和二阶泰勒动态相量模型的同步相量测量方法.先用改进矩阵束估计电网基波频率,然后结合泰勒二阶多项式与最小二乘法修正频率估计值,同时求出同步相量的幅值与相角参数,最后使用我国同步相量检测规范中的测试案例对所提算法进行仿真测试,验证本文算法的准确度和实用性.
1泰勒动态相量模型
根据电力系统同步相量标准可知,在不含噪声等干扰的理想环境下,配电网电压波形可用如下模型表示:
式中:A,φ1和f1分别为电压波形的幅值、初相位和基波频率,在理想的电网中,它们均为常数.由于负荷动态变化和噪声干扰等因素存在,实际电力系统中电压波形的幅值和频率会动态变化,考虑时变幅值和频率的电压波形动态模型可表示为:
式中:令P(t)=A(t)ejφ(t),易知P(t)能够表征电压幅值和频率随时间变化的特征,被称为动态相量.
基于动态相量的时变特性,将P(t)用二阶泰勒多项式表示为
式中:系数p0、p1和p2分别为动态相量P(t)的零阶导数、一阶导数和二阶导数.此处也可以使用高阶泰勒多项式,但是二阶多项式已经能够提供符合标准要求的测量精度.将式(3)代入式(2)中整理可得:
式中:“*”代表共轭运算符.
在实际电网中,电压/电流信号中还有基波成份以外谐波与间谐波成份.信号模型(4)只考虑电网中的基波成份,无法精确表征含有谐波和间谐波分量的电网信号.因此将(4)扩展为多频动态相量模型为
(5)式中:M代表电网信号中的频率成份数,P(ht)是第h个频率分量对应的动态相量,亦称动态谐波(或间谐波)相量.
假设以采样频率fs对电网电压x(t)进行离散采样,则离散化后得到的N点采样序列为:
式中:T=1/fs且Zh=ej2πfhT,对于采样序列中的N个采样点(为了保证t=0为中心点,N取奇数),由式(6)可以得到N个线性方程:
式中:X为采样序列,pall=[p1,...,ph,...,pM]T由所有频率成份f对应动态相量的二阶泰勒多项式系数组成,且p=1/2[p(0),p(1),p(2),p*(0),p*(1),p*(2)];系统矩阵GM=[B1,...,Bh,...,BM],且Bh=[EhΠ2,E*Π];其中E是N×N对角矩阵,元素为Zk=ej2πfhkT;Π2是N×3矩阵,下标2代表二阶泰勒動态相量,其表达式为
因为求解动态相量就是求解系数向量pall.因为X已知,若是已知GM,系数向量pall可用最小二乘法求出:
式中:“H”是埃尔米特复共轭转置运算符,若已知Z,则能求出系数向量.由Zh=ej2πfhT可知,频率fh的精确度会直接影响到最后动态相量系数矩阵的准确度,本文选择改进矩阵束算法计算频率fh,实现过程如第2节所述.
2改进矩阵束算法计算同步相量
2.1矩阵束算法
在数值计算理论中,矩阵束定义为:
式中:(ft,λ)是函数g(t)和h(t)的束函数,包含了输入信号的极点特征(在本文中,信号极点就是Z=ej2πfT);λ是约束参数,为了保证约束生效,g(t)与h(t)不能是正比例关系.对于实际电网信号,本文提出的改进矩阵束算法将噪声、谐波和间谐波等看作无效干扰信息,只关注基波频率成份,所以建立如下信号模型:
式中:k代表序列索引,y(kT),x(kT)和n(kT)分别代表采样序列、理想信号序列和干扰序列.
第一步,使用采样序列中的连续N点构造(N-L)×(L+1)型Hankel矩阵如下所示:
式中:L为矩阵束参数,其取值会影响改进矩阵束算法的抗干扰性能,一般选取N/3≤L≤N/2比较合适[16].
第二步,对Hankel矩阵Y进行奇异值分解.为了区分输入信号的基波成份与干扰成份,改进矩阵束算法的核心思想是找出代表基波频率成份的奇异值,因此需要对采样信号构成的Hankel矩阵Y进行奇异值分解:
式中:U为(N-L)×(N-L)型酉矩阵,V为(L+1)×(L+1)型酉矩阵,S为包含Hankel矩阵Y所有奇异值的(N-L)×(L+1)型对角矩阵.
第三步,利用奇异值分布规律滤除噪声等干扰成份.对于无噪声或者其他干扰的理想信号,矩阵S的对角元素会以一对降序排列的非零奇异值σ1和σ2开始,其余元素均为0.但是当噪声等干扰存在时,矩阵S的其余对角元素便不再为零.为了将噪声干扰成份造成的奇异值与电网信号频率造成的奇异值区分开,本文使用自适应定阶方法(见2.2节)计算出频率成份个数M.然后将噪声等干扰成份对应的σ(ii=2M+1,2M+2,...)设置为零,于是得到新的奇异值对角矩阵S′.
第四步,构造矩阵束.在上一步使用奇异值分布规律滤除干扰后,可以使用U、V和S′构造矩阵束,取V的右奇异向量:
将V′去除最后一行得到V1,去除第一行得到V2,然后重构两个矩阵:
经过干扰滤除和重构之后,Y1和Y2被认为由理想信号构成,如下所示:
经过上述步骤处理后得到的Y1和Y2不会满足正比例关系,故可以使用Y1和Y2构造矩阵束F(λ)=Y2-λY1.
第五步,提取矩阵束极点信息,求出基波频率.由文献[15]可知,极点Z可以通过求解矩阵束F(λ)的广义特征值求出.因此可以将对Z的求解转化为对Y1+Y2特征值的求解,此处Y1+为矩阵Y1的广义伪逆矩阵:
求出Y+Y的特征值Z后,结合Z=ej2πfhT可以得到电网信号的基波频率为:
2.2自适应定阶方法
对于如式(5)所示的信号模型,每个频率fh成份会使奇异谱中出现一对连续的奇异值,分别处于奇异谱序列的奇数与偶数位置.一般来说,由电网信号频率成份产生的奇异值远远大于因噪声而产生的奇异值.定阶算法需要将有效信号成份尽可能从背景噪声中区别出来,才能保证矩阵束算法准确计算信号各成份的频率值.基于此,本文提出一种基于奇异值均值的自适应定阶方法,其步骤如下.
第一步,将奇异值分奇偶位置进行重新排序
其中σ为奇异值矩阵S的对角线元素;
第二步,计算每个频率fh对应奇异值的均值,即奇异值均值序列
第三步,对奇异值均值序列进行归一化,求出奇异值均值归一化序列Snor,各元素为
其中p,为San的第i个元素,pmar为Sman的第一个元素(也是值最大的元素).
第四步,定义噪声奇异值的均值阈值η为
第五步,令M为序列Snor中所有大于η的个数,即为电网信号频率成份个数.
2.3同步相量参数计算
求出电网信号各频率fh之后,结合公式(9)就能求出多频动态相量系数向量pall=[p1,...,ph,...,pM]T,其中的基波动态相量系数为
故同步相量的相位角参数为
同步相量的幅值参数为
修正后的基波频率参数为
式中:“∧”代表测量值;f、A和φ分别为本文提出算法测量出来的电网同步相量参数,即为电网基波成份对应的频率、幅度和相位值.
2.4算法流程图基于改进矩阵束的动态同步相量测量方法流程
如图1所示.首先将采样信号序列构造成Hankel矩阵;接着对Hankel矩阵进行奇异值分解处理,利用奇异值序列进行自适应定阶得到电网信号中的有效频率成份数M;然后根据奇异值分解结果和频率成份数M构建矩阵束,求解矩阵束的特征值后求出各信号成份的粗估计频率值;最后利用求出的粗频率值构建基于二阶泰勒动态相量模型的多频系统矩阵,并用最小二乘法估计出二阶动态相量系数,进而计算电网信号基波分量幅值、相位和频率参数,即为同步相量.
3算法测量精度分析
为了测试提出算法的精确度和鲁棒性,本文根据我国检测规范——《GB/T26862-2011电力系统同步相量测量装置检测规范》对算法的关键指标进行测试.根据重要性与实用性原则,主要从检测规范中规定的频率误差、幅值误差、相角误差、幅值调试和频率偏移影响等方面进行测试.在所有实验中,采样频率fs设置为2400Hz,观测窗口长度分别为1、2和3周期.对采样序列进行逐點滑窗计算,并取1周波(80次计算)中的最大绝对误差作为测试结果报告.另外,为直观展示本文算法改进效果,选取了TWLS算法作为对比算法进行性能分析.
3.1频率测量误差测试
我国同步相量测量装置检测规范规定,同步相量测量装置在45~55Hz范围内,频率测量误差不能超过0.002Hz.测试信号如式(29)所示.Un为电力系统额定电压.
表1中记录了改进矩阵束算法在不同频率下的频率测量最大绝对误差,可以看出,算法测量精度均在10-15数量级,完全符合标准要求,同时观测窗长对算法精度无影响.
3.2相量测量误差测试
由同步相量的定义知,相量包含幅值与相角两个基本参数.本小节根据同步相量测量标准规定分别对改进矩阵束算法的幅值和相角测量精度进行分析和评估,测试信号如式(30)所示.
(30)幅值测量误差计算公式如式(31)所示,其中额定電压Un为100/3V,电压基准值取Un的1.2倍,此处为70V.测试电压幅值选取范围为0.1Un~2.0Un,变化步长为0.1Un,标准要求在所有测量条件下的幅值测量误差不能超过0.2%.
图2中的测试结果显示,虽然改进矩阵束算法的测量精度随着电压值变大而稍微降低,其理论精度为10-13数量级,远远优于TWLS算法的10-6数量级,且观测窗长的变化对静态信号测量精度无影响.
3.2.2相角误差测试
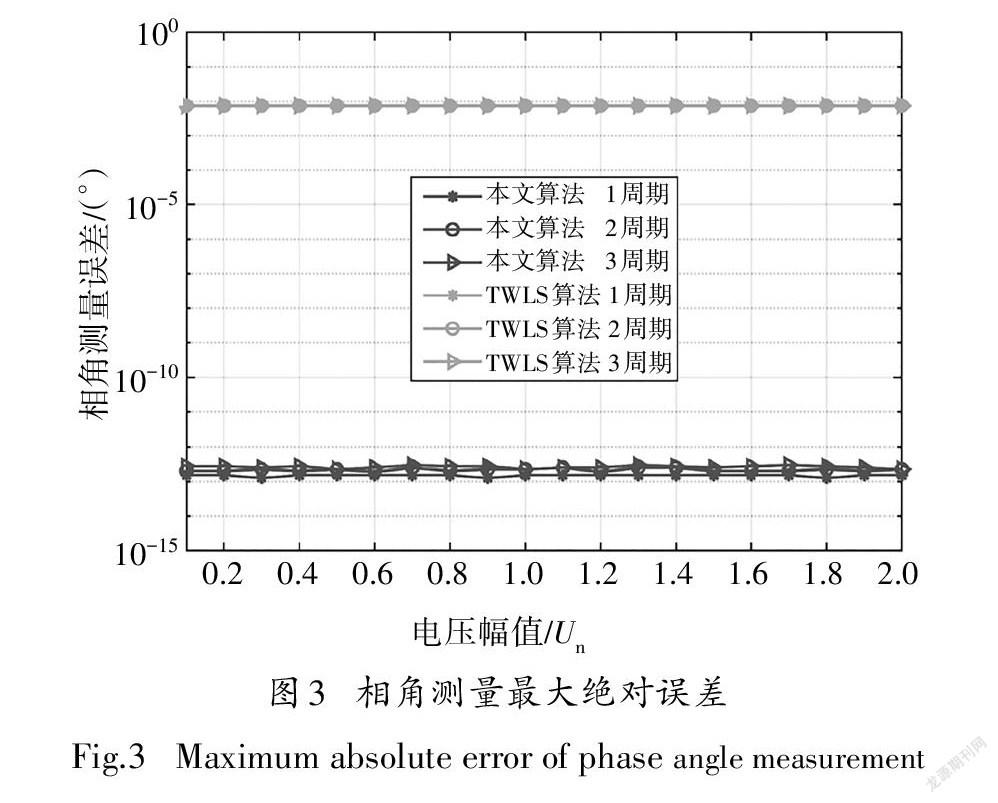
图3展示了改进矩阵束算法在不同幅值情况下量精度均能达到10-13数量级,不但满足低于0.2°的的相角测量精度.在所有测试条件下,算法的相角测要求,而且远远优于TWLS算法的数量级.与幅值测量结果不同的是,相角测量精度随着观测窗长变小而提高.
3.3幅度调制影响测试
在实际电网中,同步相量恒定不变的理想情况并不存在,相量的幅值和相角参数一定处于不同程度的动态变化中.为了保证同步相量装置对动态信号具有良好的测量性能,检测规范规定:在调制频率范围0.1~4.5Hz和幅度调制量为0.1Un测试条件下,基波电压幅值测量误差值应小于等于0.2%,相角测量误差应小于等于0.5°.在幅度调制影响测试实验中,调制频率依次增加0.1Hz,生成41组不同测试信号如式(32)所示.
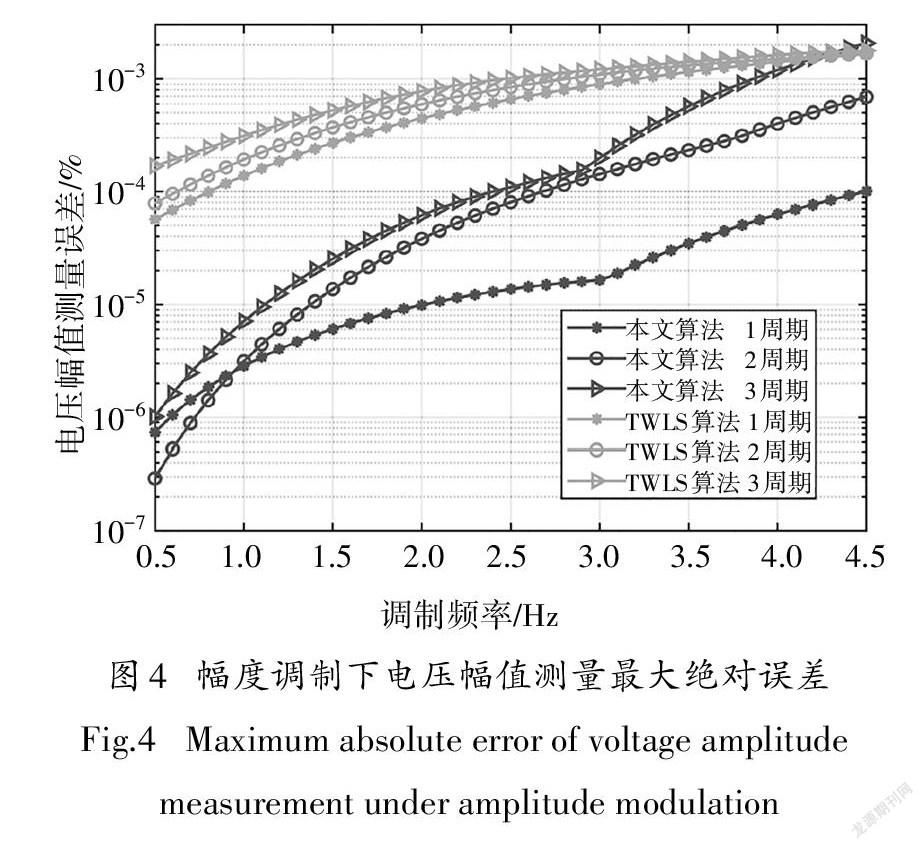
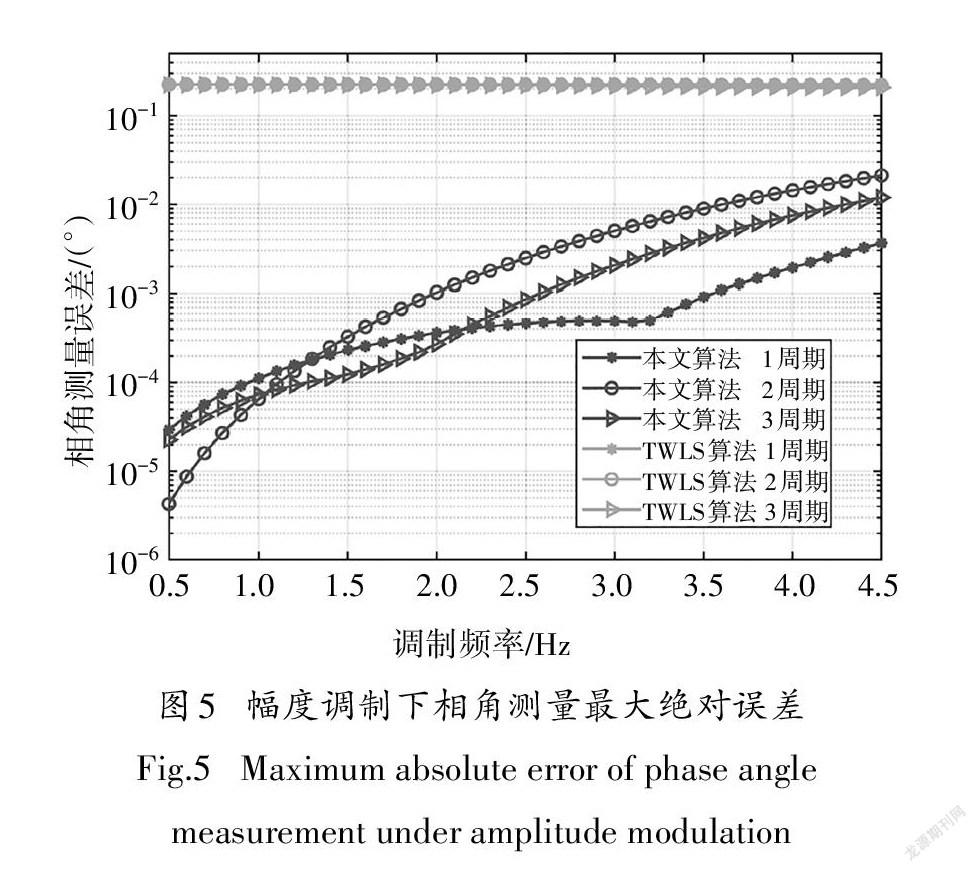
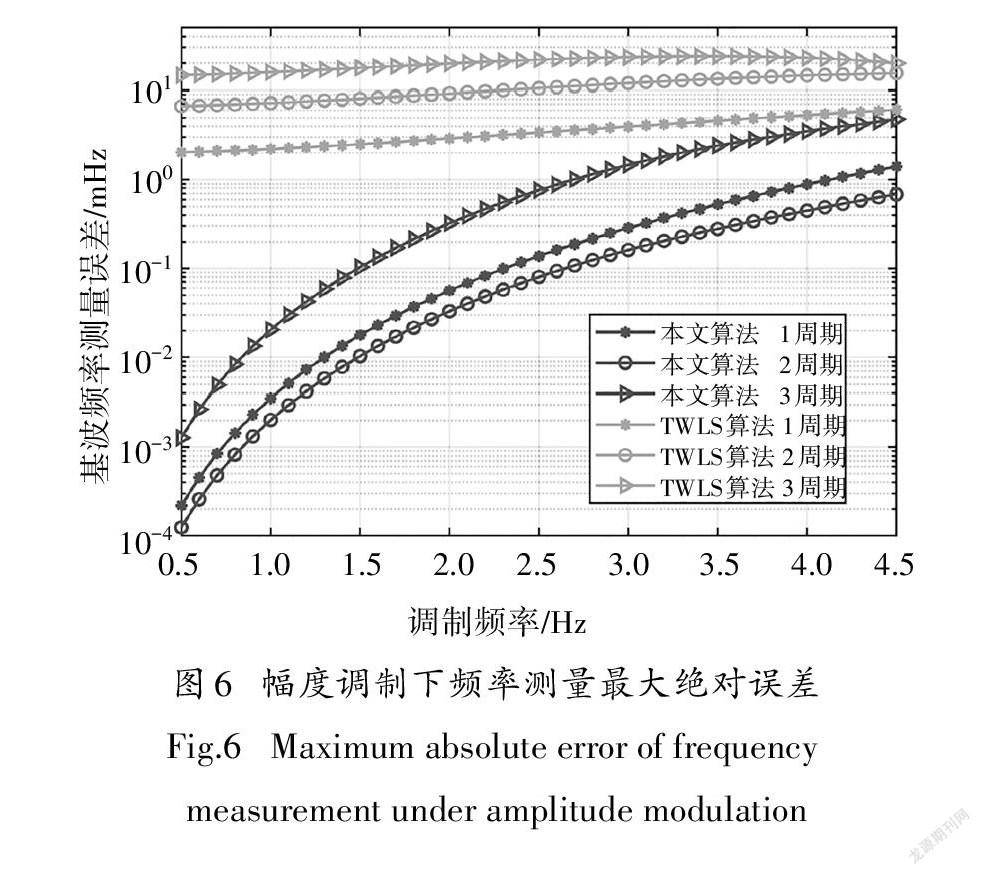
改进矩阵束算法对每组测试信号的幅值、相角和频率测量精度结果分别如图4-图6所示.从图4可以看出,在调制频率0.1~4.5Hz范围中,电压幅值测量误差均小于0.1%,完全满足检测规范的精度要求.另外幅值测量精度与调制频率大小和观测窗长有关,表现在:第一,幅值测量精度随着调制频率增大而降低;第二,幅值测量精度随着观测窗口长度增大而降低.从图5可以看出,改进矩阵束算法相角测量精度均小于0.1°,完全满足检测规范要求,同时相角测量精度随着调制频率增大而降低.与幅值测量精度结果不同,观测窗长度虽然影响相角测量精度,但是并未呈现比例关系.三种不同观测窗情况下,2周期观测窗测量结果表现较差;而在调制频率4~4.5Hz范围内,三种不同长度观测窗提供的相角测量精度一样.从图6可以看出,改进矩阵束算法的频率测量精度虽然随着调制频率增大而减小,但在各测试条件下均能优于TWLS算法.
3.4频率偏移影响测试在实际电网中,由于用电负荷与发电功率的不
平衡,会导致实际电网频率偏离标称频率,因此需要测试改进矩阵束算法在频率偏差条件下的同步相量测量性能.实验中,采用综合矢量误差指标表示测量精度,其定义如下:
式中:TVE是综合矢量误差,Pr和Pi分别为理想信号相量的实部与虚部,P(rt0)和P(it0)分别为实测相量的实部与虚部.
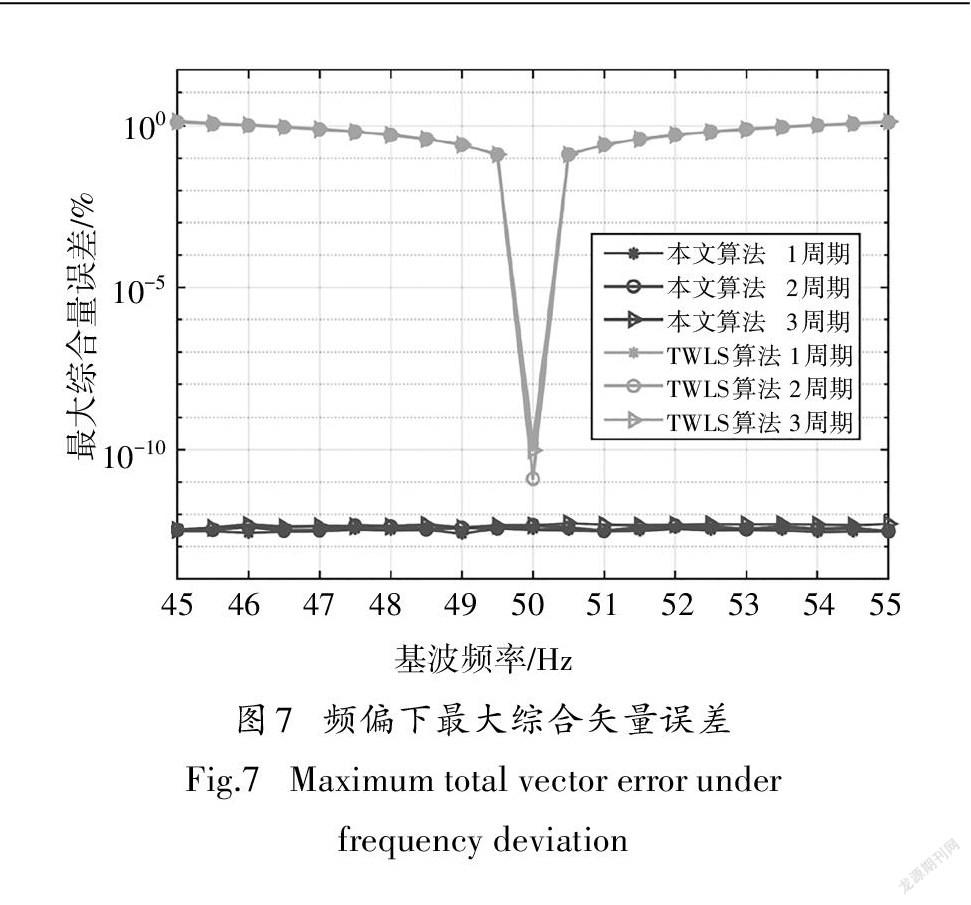
检测规范要求规定:在基波频率45~55Hz范围内,1级同步相量测量装置的综合矢量误差应小于1%.基波频率在45~55Hz之间以0.5Hz为步长进行变化,测试信号如式(29)所示,测得改进矩阵束算法的综合矢量误差如图7所示.因为TWLS算法总是以电力系统标称频率为参考值,所以测量精度受到频率偏差影响极大;而改进矩阵束算法在所有频率偏差情况下,均有很高测量精度,误差数量级小于10-12%,同时实验结果表明增大观测窗长度会导致算法的综合矢量误差变大.
4结束语
本文提出了一种基于改进矩阵束的同步相量测量算法.通过引入矩阵束算法能够在不同干扰情况下精确测量电网基波频率的优势,结合二阶多频动态相量模型可以表征同步相量变化率和加速度的特点,本文提出的算法能够精确表示电网信号的动态特性,同时也能降低谐波与间谐波成份的干扰.实验结果显示,该方法无论是在频率偏差情况下,还是在电压幅值调制情况下,均有较好的测量性能,可以精确测量电网信号的幅值、相角和频率参数.此外,利用同步相量检测规范中的测试案例,验证了提出算法的精确度和鲁棒性,具有一定的工程应用价值.
参考文献
[1]王继豪,裴茂林,熊茹,等.同步相量测量技术在配电网中的应用[J].电测与仪表,2017,54(17):1-6.
[2]李俊刚,张爱民,张杭,等.广域保护系统数据网络可靠性评估[J].电工技术学报,2015,30(12):344-350.
[3]靳宗帅.强噪声电信号宽频带相量高精度估计方法[D].济南:山东大学,2019:1-13.
[4]葛维春,蔡亦浓,李江,等.基于多分支电流混合量测的配电网三相状态估计[J].电力系统保护与控制,2020,48(9):1-10.
[5]袁明军,江浩,黎强,等.四统一四规范同步相量测量装置关键技术研究[J].电力系统保护与控制,2019,47(4):182-187.
[6]汪芙平,靳夏宁,王赞基.实现动态相量测量的FIR数字滤波器最优设计[J].中国电机工程学报,2014,34(15):2388-2395.
[7]汪芙平,黄松岭,赵伟,等.基于最优线性滤波的PMU测量I:最优滤波原理[J].中国电机工程学报,2018,38(8):2262-2271.
[8]裴茂林,严勤,汪芙平,等.谐波相量测量的FIR滤波算法[J].电测与仪表,2019,56(12):1-8.
[9]白莎,符玲,熊思宇,等.基于多频率相量模型的动态同步相量测量算法[J].中国电机工程学报,2018,38(13):3748-3755.
[10]金涛,陈毅阳,段小华,等.基于改进DFT的电力系统同步相量测量算法研究[J].电工技术学报,2017,32(17):1-10.
[11]张晓莉,许勇,刘慧海,等.一种提高同步相量测量装置动态性能的新算法及其测试研究[J].电力系统保护与控制,2015,43(18):48-54.
[12]刘洁波,黄纯,江亚群,等.基于强跟踪泰勒-卡尔曼滤波器的动态相量估计算法[J].电工技术学报,2018,33(2):433-441.
[13] BELEGA D,FONTANELLI D,PETRI D. Dynamic phasor and frequency measurements by an improved Taylor weighted least squares algorithm[J]. IEEE Transactions on Instrumentation and M e a s u r e m e n t ,2 0 1 5 ,6 4( 8 ):2 1 6 5 - 2 1 7 8 .
[14] CHEN L,ZHAO W,WANG Q,et al.Dynamic harmonic synchro⁃phasor estimator based on sinc interpolation functions[J].IEEE Transactions on Instrumentation and Measurement,2019,68(9): 3054-3065.
[15] SARKAR T K,PEREIRA O.Using the matrix pencil method to estimate the parameters of a sum of complex exponentials[J]. IEEE Antennas and Propagation Magazine,1995,37(1):48-55.
[16]康小寧,屈亚军,焦在滨,等.基于最小二乘矩阵束算法的工频分量提取方法[J].电力系统自动化,2014,38(21):66-70.

