基于认知水平分析的习题选择与编制
浙江宁波市奉化区教师进修学校(315502) 宋煜阳
“双减”背景下,提高作业设计质量成为学校和教师的核心工作之一。作业设计的质量,关键在于习题的选择与编制。一道习题的“好”与“坏”,主要取决于习题的情境、知识和认知水平三个核心元素。
本文以顾泠沅教授的认知水平理论为依据,采用核心知识评价维度的构建、习题认知水平的划分和不同认知水平之间的升级等策略,实施基于认知水平分析的习题选择和编制。
一、建立评价框架,确定习题内容设计的维度
作业减量提质,需要在习题内容设计的维度上下功夫。习题内容设计维度的确定,关键在于能否建立科学、合理的评价框架。其中,概念模型理解与多元表征、能力评价指标体系构建是形成评价框架的重要手段。
1.把握概念的模型、理解目标与表征方式,实现习题内容维度的全覆盖
数学概念既是数学学习的重要基础,又是习题内容设计的重要对象。在设计时,一方面要明确概念学习的目标,在结果性目标上是要达到“了解”“理解”“掌握”“运用”中的哪个学习水平,需要实现“经历”“体验”“探索”中哪个过程性目标;另一方面,要明确概念在不同学习阶段的具体模型和目标要求,丰富表征方式,在某个概念配套练习的内容维度上实现全面覆盖,确保概念理解的整体性和进阶性。
比如“乘法”概念,具体模型有求和模型、倍的模型、面积模型、搭配模型四种,主要在二、三年级集中学习。其中,人教版教材二年级上册表内乘法单元,乘法含义定位为求和(求几个相同加数的和)模型。口诀“二四得八”练习的目标为“理解‘二四得八’乘法口诀的含义,能在具体情境中区分2个4和4 个2”“知道乘法算式各部分名称,能区分加法和乘法算式”两个目标。
相应练习可以设计为图1 涂补花瓣的形式,其中①②③都是围绕乘法算式各部分名称来表征的,而在乘法口诀含义理解的表征比较丰富:选项④用数间隔的情境表示“4 个2”;选项⑤用点子图表示“2 个4”或“4 个2”;选项⑥用数形结合的情境表示“4 个2”;选项⑧用算式连加表示“2 个4”。该练习始终围绕“求几个相同加数的和”这一乘法模型展开,形式活泼,素材全面,层次分明。
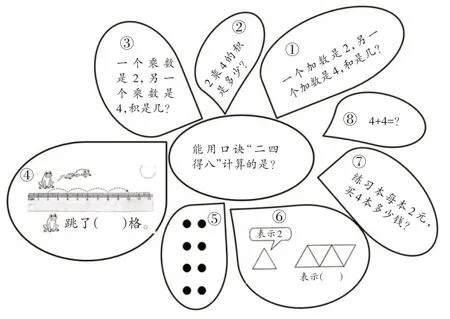
图1
在三年级下学期,学生经历了求和、倍、面积、搭配等多个模型的学习,对乘法概念已经相当熟悉,这时就可以设计多个模型辨析的综合练习:下面哪些数学问题能够用算式24×3 来解决?(1)三(1)班买了3 个足球,每个足球24 元。买足球一共花了多少钱?(2)聪聪今年24 岁,爷爷今年的年龄是聪聪的3 倍,爷爷今年多少岁?(3)明明画了一个长24厘米、宽3厘米的长方形。这个长方形的面积是多少平方厘米?(4)三(2)班有24 本不同的科普书,3 本漫画书。每次只能借一本科普书和一本漫画书,一共有多少种不同的借书方法?四个小题分别对应了求和模型、倍的模型、面积模型和搭配模型。
上述习题均围绕乘法概念模型展开,由于不同学习阶段对概念模型内涵要求不同,概念表征的维度也就发生了变化,习题的宽度自然也不尽相同。
2.构建关键能力评价指标分析框架,实现习题内容维度的系统性
要实现教、学、评一致性,就需要构建关键能力评价指标体系。运算能力是一项关键数学能力,能力指标体系主要包括正确运算、理解算理、方法合理3个评价维度和9个二级指标。其中正确运算维度包含运算结果的正确性、运算程序的规范性、运算速度的标准性3 个二级指标;理解算理维度包含算理表述的正确性、算理表征的层次性、算理迁移的通用性3 个二级指标;方法合理维度包含运算方法的多样性、运算过程的简洁性、运算方法的创新性3 个二级指标。对照运算能力评价指标分析框架,“100 以内不退位减法”的练习就可以对标设计(如表1)。
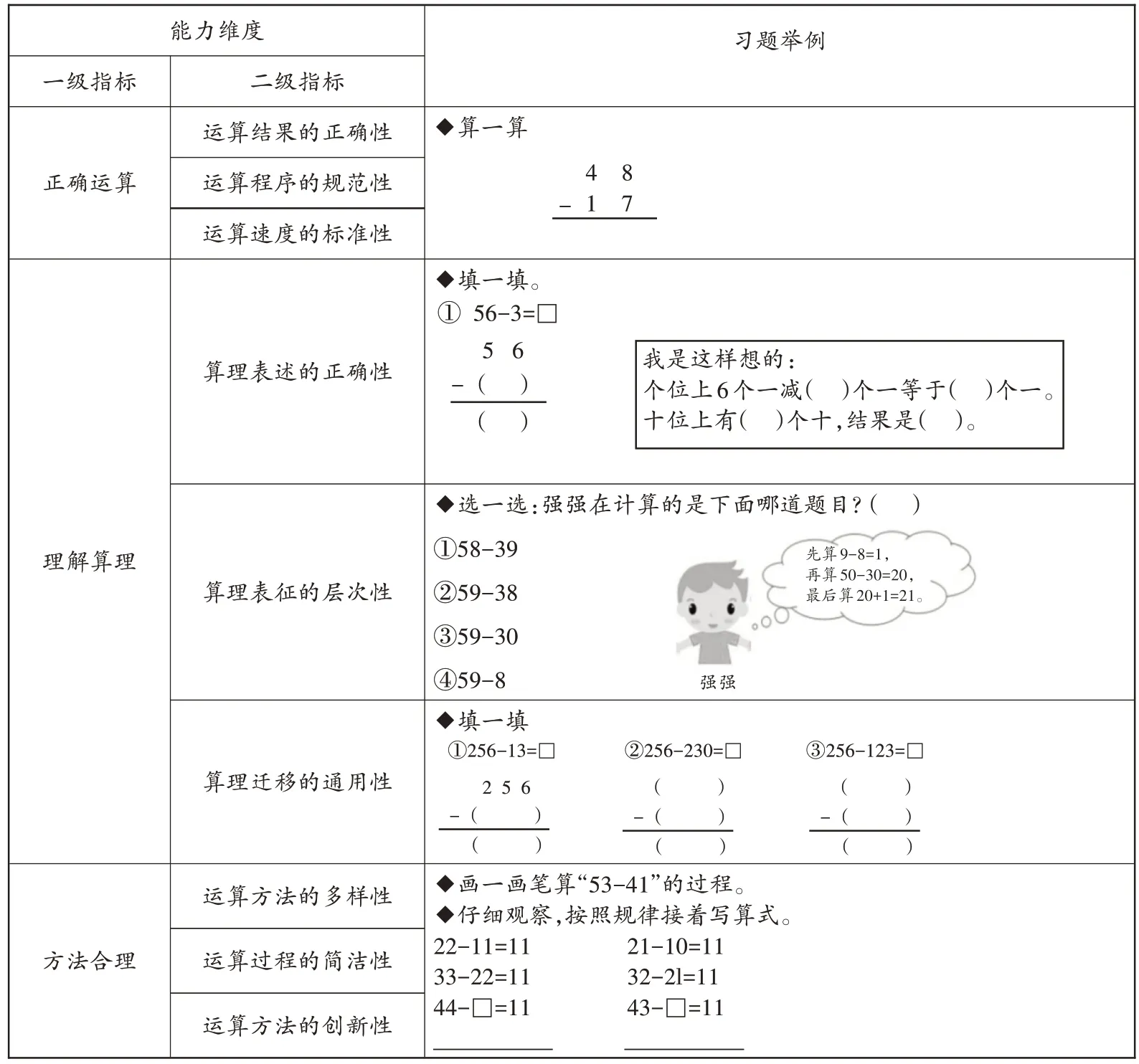
表1
每个具体的教学内容,都指向一定的关键能力。如果明确了数学关键能力,构建了相应的能力评价指标体系,并以此作为练习设计的依据,练习就具备了较强的系统性,也实现了教、学、评一致性。
二、了解认知水平,确定习题认知水平的层级
同一个概念,可以设计不同认知水平的习题。依据顾泠沅教授的认知水平理论,习题认知水平可以划分为四个水平层级:水平一,操作性记忆水平;水平二,概念性记忆水平;水平三,说明性理解水平;水平四,探究性理解水平。比如,“平均数”概念,根据学生的认知水平可以设计以下四题:
(1)某小组6 名学生的身高分别为139 cm、140 cm、135 cm、138 cm、139 cm、137 cm。求小组的平均身高。
(2)判断正误:学校排球队队员的平均身高是160 cm,有的队员身高会超过160 cm,有的队员身高不到160 cm。
(3)聪聪和明明都是四(1)班的学生,他们班在排座位时,个子矮的学生坐前面,个子高的学生坐后面。聪聪计算出第一排学生的平均身高是130 cm,明明计算出第一列学生的平均身高是135 cm。你觉得哪一个数更接近全班学生的平均身高?为什么?
(4)有甲、乙、丙、丁四个数,每次去掉一个数,求出其余三个数的平均数,这样算了4次,得到57、76、89、98 四个数。甲、乙、丙、丁四个数的平均数是多少?
上述四题分别考查直接利用平均数计算方法求出一组数据的平均数,平均的意义,根据平均数概念的内涵进行不同方向的解释说明,开放拓展共四个层面,分别对应操作性记忆水平、概念性记忆水平、说明性理解水平和探究性理解水平四个水平。
在习题认知水平划分时,可以根据学生的学习表现、行为关键词加以识别,作为确认习题认知水平的操作要领,具体可参照表2。
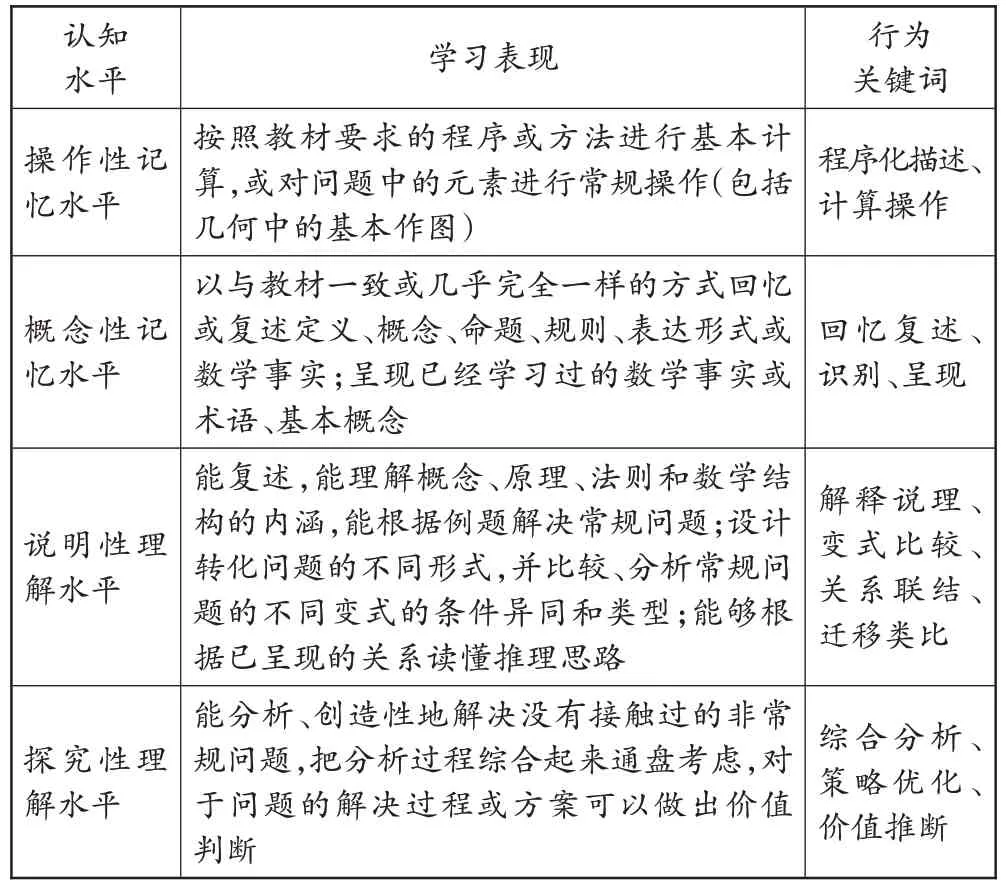
表2
习题认知水平划分一般包括三个步骤:(1)结合教学内容,确定行为关键词;(2)拟定学生行为描述;(3)对照学生行为描述寻找对应的习题。
以人教版教材三年级下册“面积和面积单位”内容为例,例题对应的“做一做”和练习十四部分习题划分如表3所示。

表3
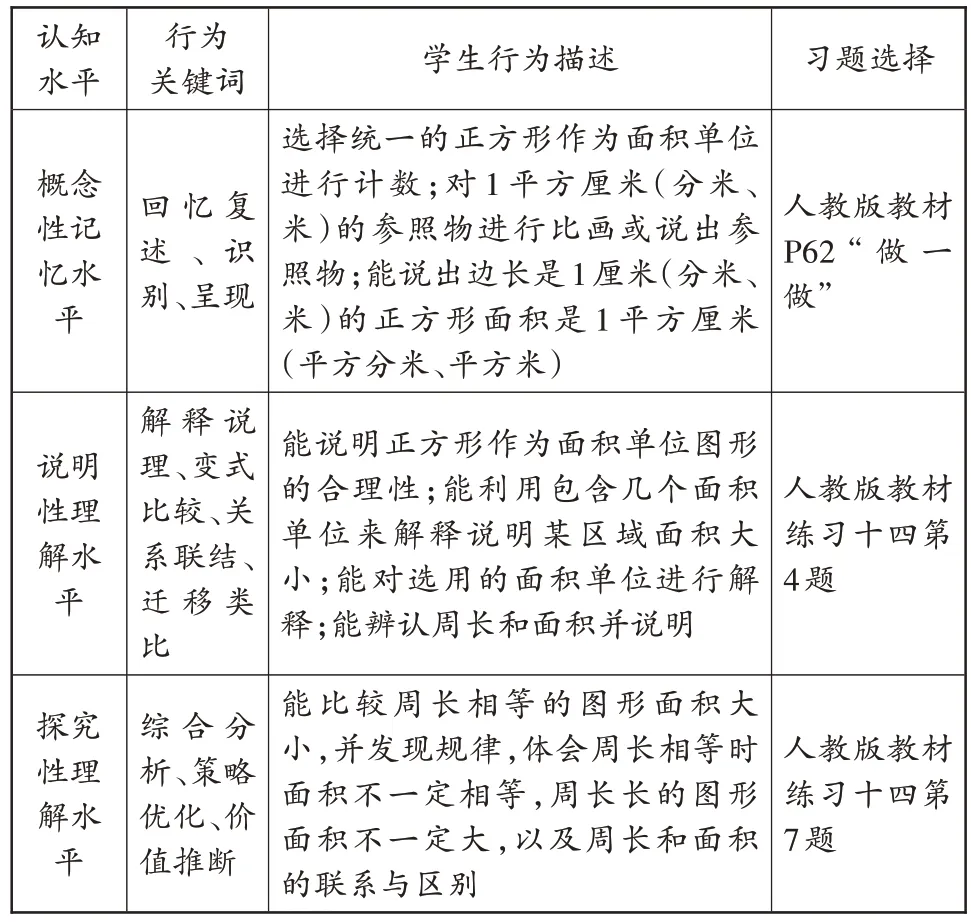
续表
需要指出的是,有些习题可以作为不同认知水平来训练,具体水平取决于教师的认识与应用。如人教版教材练习十四第5 题“在横线上填写合适的单位名称”中的“黑板长4( )”,如果教师只是机械化地告知学生“看到长就填写长度单位”就变成概念性记忆水平了,而让学生说明为什么填“米”这个单位,则是说明性理解水平。
三、明确选编要领,把握习题认知升级的节点
学习者需要经历不同认知水平习题的训练。因此,低认知水平的习题本身并非坏题,只是习题训练不能总在低认知水平层面打转。选择和编制习题时,需要明确认知水平的设计要领,把握认知升级节点,从而实现有序升级。
1.低认知水平习题设计,需要减少简单机械的记忆,加强变式,重视对核心知识和活动经验的复现
概念性记忆水平的习题训练是有必要的,但需要减少简单机械的、非本质的概念性记忆考查。比如,判断题“含有未知数的式子就是方程”,就是考查学生能否复述“含有未知数的等式就是方程”这个定义。而这个定义本身就是形式化的,不能反映方程的本质,这样的记忆就没有必要,相关的判断题也就无实际意义。
相反,部分核心知识和必要的活动经验表象是需要强化的。比如,数位顺序表、十进制计数法都是核心知识,需要理解和有意义记忆。又如,“一个2 分硬币约重 1g”“1 分钟有多长”“一拃约 20 厘米”等常见单位参照物、身体尺的表象,需要学生在实践活动中逐步感知,以形成较好的量感。另外,当地人口数、标志性建筑面积等,都需要学生加以了解,这部分生活常识也是数学实践性习题必不可少的一部分。
2.高认知水平习题设计,需要还原情境的现实性,加强题目呈现的多元性,降低题目的结构化;注重结论探索的过程性与开放性、结论应用的实践性与创造性
习题从低认知水平向高认知水平升级,需要在现实情境还原、呈现方式多元、结论探索过程性与开放性、实际应用等方面下功夫。
比如,将题目“一袋方便面现在的质量是120克,比增量前多25%。你知道增量前是多少克吗?”中的“比增量前多25%”调整为“增量25%,加量不加价”,以生活中的广告语对现实情境加以还原,就能降低数学结构化成分,但需要学生把生活语言抽象为数学语言。
呈现方式多元,需要加强图文结合、对话的呈现方式,需要加强多条信息、多幅图示信息的切换,重在训练学生对关键信息的提取、条件与问题的分析选择。结论探索过程性与开放性,常见于公式推导、概念习得过程和原理解释,如“描述三角形面积公式推导过程”“为什么草原上蒙古包底面是圆形的”“为什么合格率不会超过100%”等。实际应用主要表现为实践性活动,如利用身体尺测量篮球场一圈的长度,通常会涉及方案策划、策略优化等。
当然,高认知水平习题还包括题组观察、规律发现和结论开放等类型。如,聪聪家距离学校400米,明明家距离学校700 米,聪聪家距离明明家多少米?这就需要考虑两家是否在同一直线上,或是同一直线上的两家是在学校两侧还是同侧等多种情形,从而考查学生有序分析问题的能力。
总之,习题是教、学、评一致性的重要载体。教学中,日常作业批改与试题评价反馈,除了关注对错与得分,更需要重视认知水平分析。基于认知水平分析的习题选择与编制,是一线教师开展习题研究、实现减负提质的可行路径。

