基于佳点集和莱维飞行原理的蜉蝣优化算法

吴霄，江海新，吴芸，吴雪颜，江佳玉，童林

基于佳点集和莱维飞行原理的蜉蝣优化算法

吴霄，江海新，吴芸，吴雪颜，江佳玉，童林

（九江学院 理学院，江西 九江 332005）

针对蜉蝣优化算法（Mayfly Algorithm，MA）在求解多峰函数时容易发生早熟收敛而陷入局部极值的缺陷，提出了一种基于佳点集和莱维飞行原理的蜉蝣优化算法（JLMA）．该算法首先采用佳点集初始化替代随机初始化，以增强初始种群的遍历性；然后修改了雄性蜉蝣的位置更新公式，消除了速度项对收敛速度的影响；最后，利用莱维飞行改变雄性蜉蝣位置的移动方向，防止算法陷入局部最优．在12个测试函数上的实验结果表明，JLMA算法能跳出局部最优，提高解的精度，寻优效果更好．

蜉蝣优化算法；佳点集；莱维飞行

传统优化算法一般要求优化问题是线性或可导的，然而，现实问题往往是非线性或不可导的．为了克服传统优化算法的缺点，群智能优化算法应运而生，如粒子群算法（Particle Swarm Optimization，PSO）、遗传算法（Genetic Algorithm，GA）、差分进化算法（Differential Evolution Algorithm，DE）等．

蜉蝣优化算法（Mayfly Algorithm，MA）是Konstantinos Zervoudakis[1]于2020年提出的新型群智能优化算法，它的灵感来源于蜉蝣的社会行为，特别是它们的交配过程．MA算法应用广泛，已被用于线性天线阵列的模式合成优化[2]，集成风速预测系统[3]，与电解制氢系统相结合的光伏热能收集器的性能预测[4]等不同领域．在求解某些优化问题时，MA算法存在收敛速度慢、易陷入局部最优等缺陷．针对这些缺陷，很多学者提出了不同的改进策略．Zhao J[5]等利用混沌数来代替MA算法中所涉及的随机数，并对速度公式进行修正．陈伟超[6]等改变原算法在变异上的操作，将随机选择个体的随机维度向全局最优个体的随机维度靠近，并利用倒位操作，使最优个体的位置发生倒转，提高了算法跳出局部最优的能力．王义[7]等引入自适应惯性权重衰减因子来平衡算法的探索和开发能力，并采用Lévy飞行和黄金正弦因子解决算法易陷入局部最优的缺点，增强了种群多样性，提高了算法的收敛精度．虽然已有大量MA算法的改进研究，但因蜉蝣在移动过程中步长较短，导致算法收敛速度慢、易陷入局部最优等缺陷仍存在．为此，本文提出了基于佳点集和莱维飞行原理的蜉蝣优化算法（JLMA）．

1 蜉蝣优化算法

1.1　算法原理

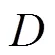
1.2　雄性蜉蝣的运动

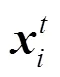
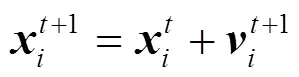
考虑到雄性蜉蝣在水面上表演交配舞且速度不能很大，因此，雄性蜉蝣的速度更新公式为

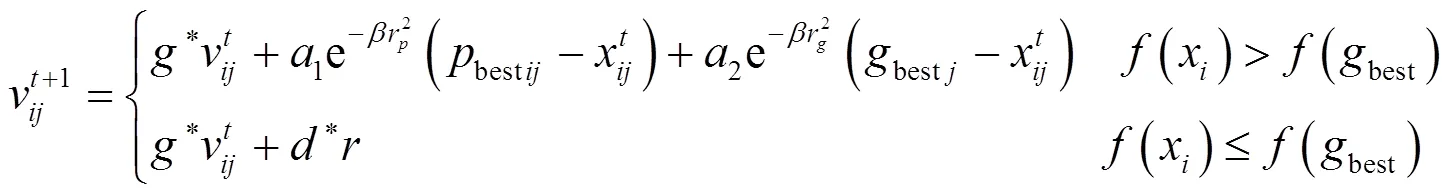
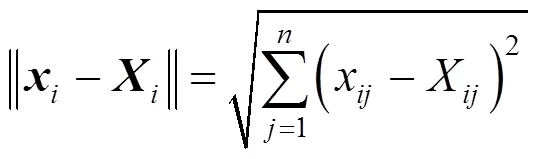
1.3　雌性蜉蝣的运动

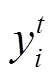
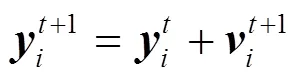
雌性蜉蝣速度的更新公式

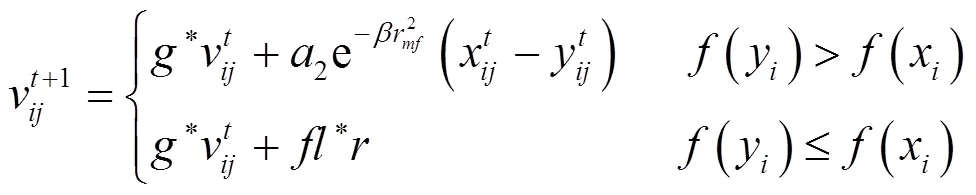
1.4　蜉蝣的交配

雌雄交配是蜉蝣的生物特性，其交配过程是从雄性种群中选择一个父本，从雌性种群中选择一个母本，最好的雌性与最好的雄性繁殖，次好的雌性与次好的雄性繁殖，以此类推．具体交配公式为

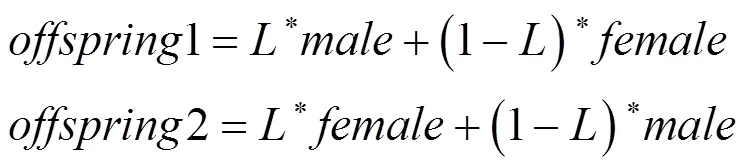
随后，交配得到的子代随机进行变异操作，并分为雄雌种群．

2 基于佳点集和莱维飞行原理的蜉蝣优化算法

2.1　佳点集原理

图1 初始种群在二维空间的分布

2.2　莱维飞行

莱维分布是法国数学家莱维（Lévy）于20世纪30年代提出的一种概率分布，事实上自然界中的许多随机现象，如苍蝇、鲨鱼的飞行轨迹均符合莱维分布．莱维飞行[10-11]服从莱维分布，是一种短距离搜索与偶尔较长距离行走相间的移动方式．莱维飞行的位置更新公式为

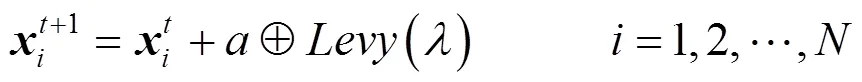
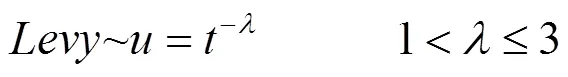
在实际应用中，莱维飞行常使用Mantegna算法模拟，相关数学表达式为

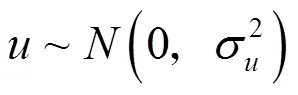
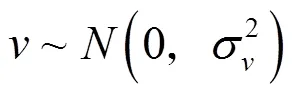
其中

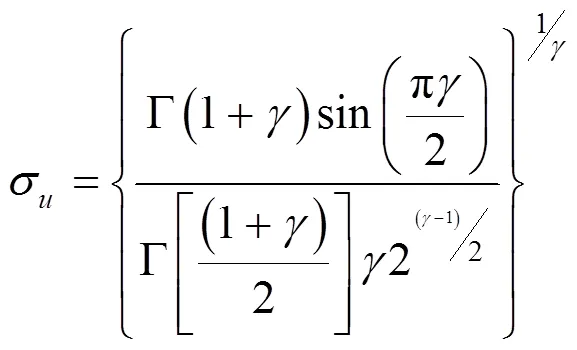
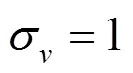
2.3　JLMA算法步骤

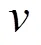
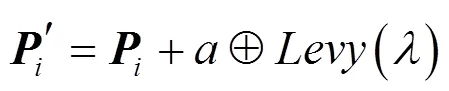
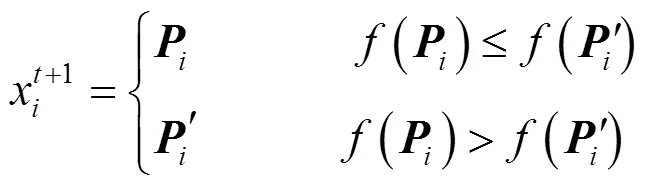
算法具体步骤：

Step 1 设置JLMA算法所需参数，利用佳点集原理初始化雌雄蜉蝣的位置，雌雄蜉蝣的初始速度设为零；

Step 2 计算蜉蝣个体的适应度值，找出当前的个体最优和全局最优；

Step 3 将莱维飞行加入雄性蜉蝣，根据式（13）～（15）更新雄性蜉蝣位置；

Step 4 根据式（4）（5）更新雌性蜉蝣的速度和位置；

Step 5 更新个体最优和全局最优；

Step 6 对雌雄蜉蝣进行排序，根据式（6）雌雄蜉蝣交配，产生子代，并对生成的子代进行变异操作；

Step 7 评估子代的适应度值，将子代分为雌雄，更新个体最优、全局最优和相关参数；

Step 8 判断算法是否满足最大迭代次数或精度要求，若满足则算法停止搜索，输出最优值；否则返回步骤Step 2继续搜索．

2.4　算法复杂度分析

3 实验仿真与分析

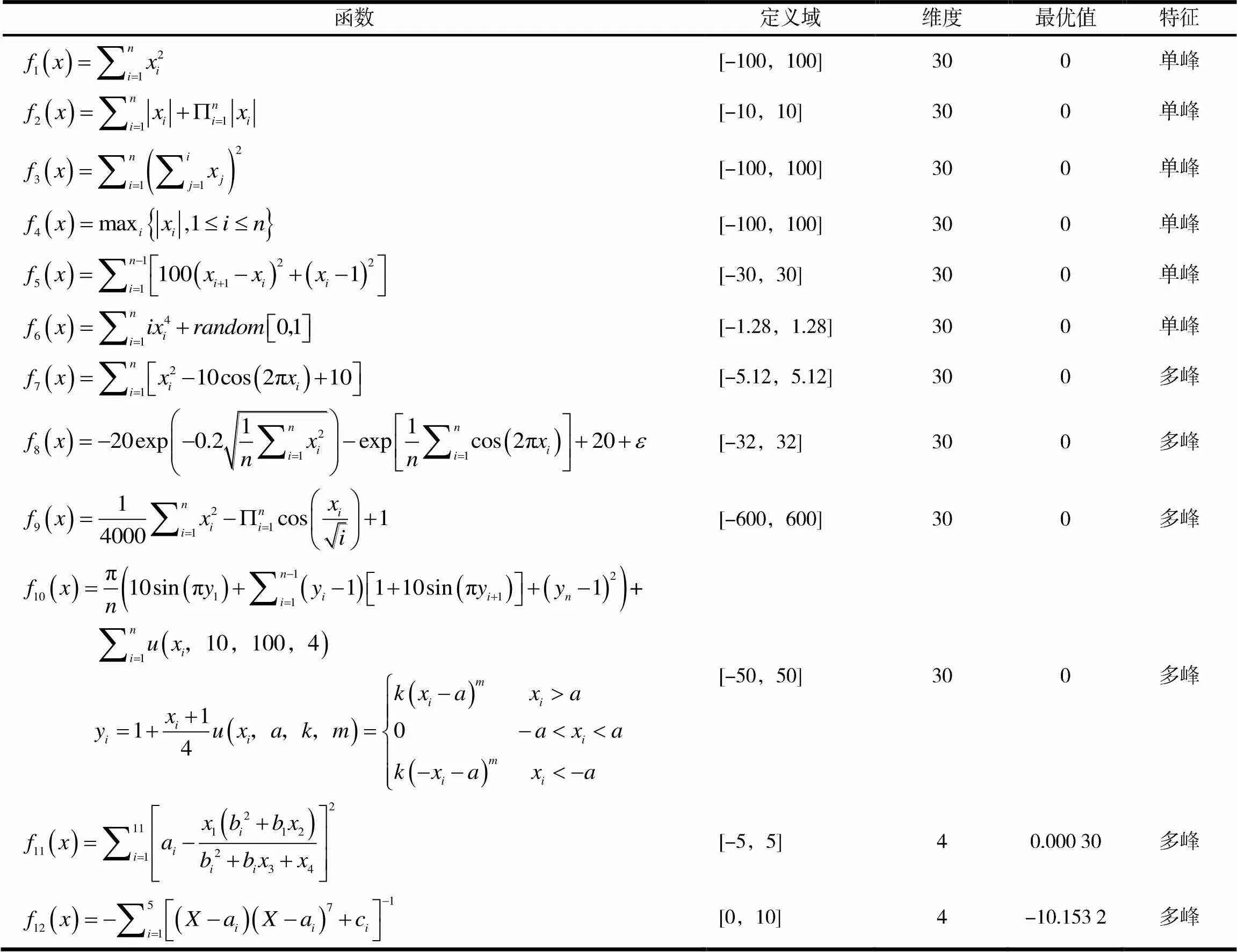
表1 基准测试函数

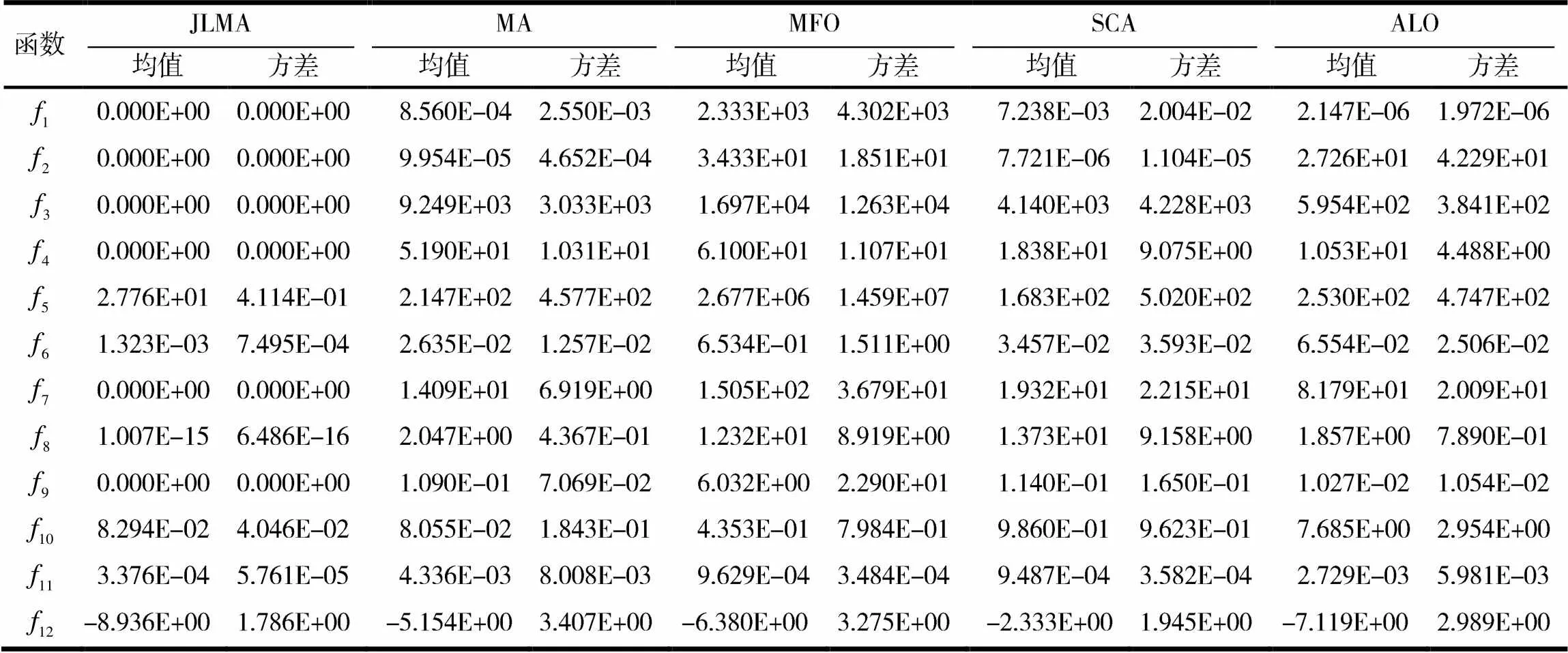
表2 不同算法在测试函数上的求解结果比较

为了更直观地比较算法的性能，观察不同算法之间收敛速度的差异，本文绘制了4个典型函数的收敛曲线（见图2）．

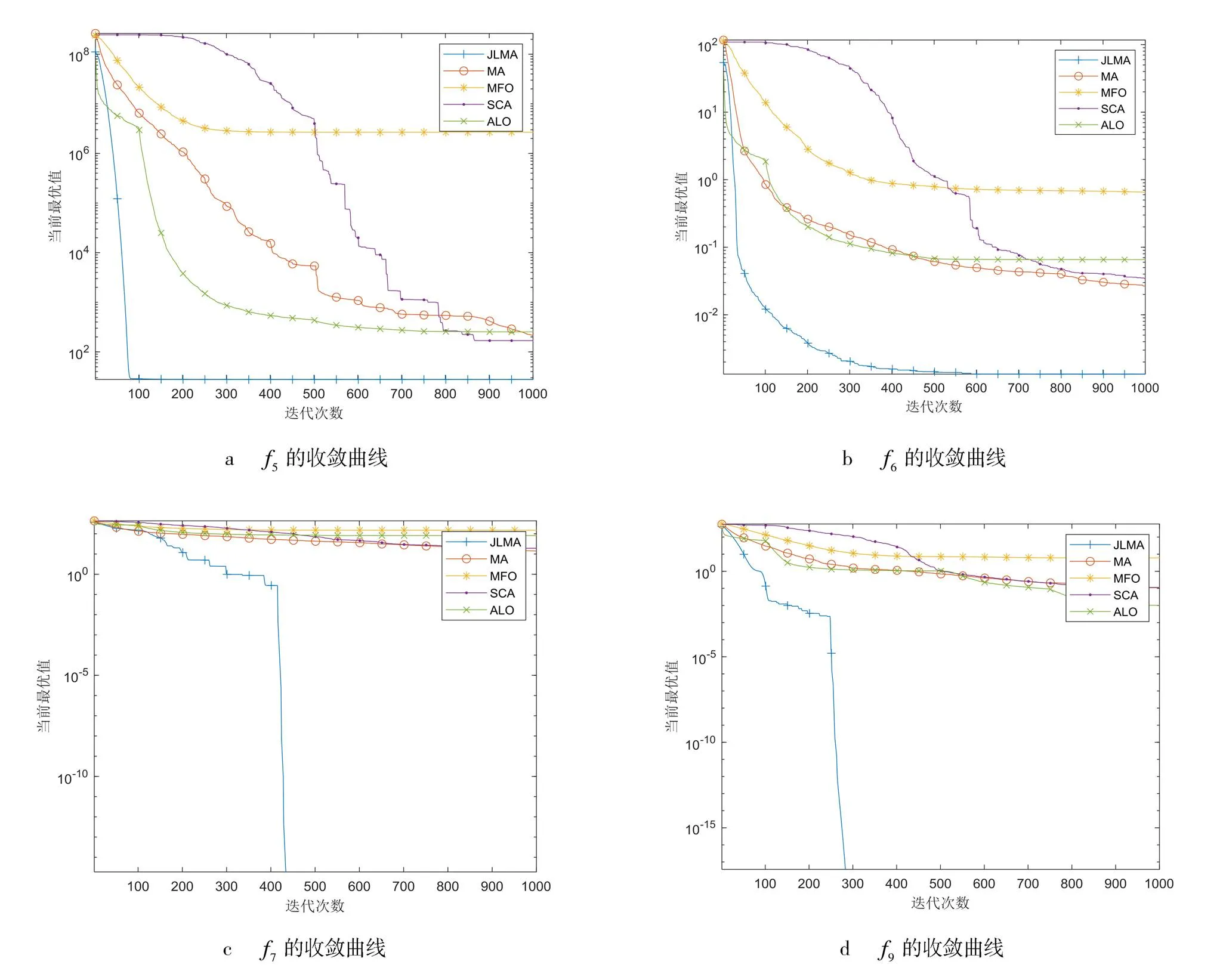
图2 不同函数的收敛曲线

由图2可知，JLMA算法的收敛速度和求解精度均优于其他算法．由图2a～b可看出，JLMA算法中的佳点集初始化，使得初始种群的质量得到提高，加快了算法早期的收敛速度；图2c～d显示，莱维飞行使算法有能力跳出局部最优，找到全局最优解．

4 结语

本文为改进MA算法易陷入早熟收敛的现象，基于佳点集和莱维飞行的数学性质，采用佳点集初始化种群位置，以提高初始种群的均匀性和遍历性，同时修正雄性蜉蝣位置更新公式，引入具有跳跃性的莱维飞行，使算法具有跳出局部最优的能力．改进后的蜉蝣优化算法（JLMA）与4个对比算法在12个测试函数中的对比实验证明了算法的优越性，并已被应用于焊接梁设计问题．

[1] Zervoudakis Konstantinos，Tsafarakis Stelios. A mayfly optimization algorithm[J]. Computers & Industrial Engineering，2020，145：106559．

[2] Xia Kewen，Wang Ting，Umar Abubakar．Pattern Synthesis of Uniform and Sparse Linear Antenna Array Using Mayfly Algorithm[J]. IEEE Access，2021，9：77954．

[3] Liu Zhenkun，Jing Ping，Wang Jianzhou，et al. Ensemble forecasting system for short-term wind speed forecasting based on optimal sub-model selection and multi-objective version of mayfly optimization algorithm[J]．Expert Systems with Applications， 2021，177：114974．

[4] Mohamed Abd Elaziz，Senthilraja S，Mohamed Zayed E，et al. A new random vector functional link integrated with mayfly optimization algorithm for performance prediction of solar photovoltaic thermal collector combined with electrolytic hydrogen production system[J]. Applied Thermal Engineering，2021，193：117055．

[5] Zhao Juan，Gao Zheng-Ming．The improved mayfly optimization algorithm with Chebyshev map[J]. Journal of Physics：Conference Series，2020，1684：012075．

[6] 陈伟超，符强．基于倒位变异的蜉蝣优化算法[J]．计算机系统应用，2021，30（8）：157-163．

[7] 王义，张达敏，张琳娜，等．基于黄金正弦与自适应融合的蜉蝣优化算法[J]．计算机应用研究，2021，38（10）：3072-3077．

[8] 王培崇，李丽荣，高文超，等．应用佳点集的混合反向学习人工鱼群算法[J]．计算机应用研究，2015，32（7）：1992-1995．

[9] 陈毓隆．改进蝴蝶算法及其在多模态优化和SVM优化的应用[D]．南宁：广西大学，2019．

[10] 王庆喜，郭晓波．基于莱维飞行的粒子群优化算法[J]．计算机应用研究，2016，33（9）：2588-2591．

[11] 李荣雨，王颖．基于莱维飞行的改进粒子群算法[J]．系统仿真学报，2017，29（8）：1685-1691，1701．

[12] Mirjalili Seyedali．Moth-flame optimization algorithm：A novel nature-inspired heuristic paradigm[J]．Knowledge-Based Systems，2015，89：228-249．

[13] Mirjalili Seyedali．SCA：A Sine Cosine Algorithm for solving optimization problems[J]．Knowledge-Based Systems，2016，96：120-133．

[14] Mirjalili Seyedali．The Ant Lion Optimizer[J]．Advances in Engineering Software，2015，83：80-98．

mayfly optimization algorithm based on good-point set and Lévy flight principle

WU Xiao，JIANG Haixin，WU Yun，WU Xueyan，JIANG Jiayu，TONG Lin

（School of Science，Jiujiang University，Jiujiang 332005，China）

To address the shortcoming that the mayfly algorithm（MA）is prone to premature convergence and falling into local stagnation when solving multimodal functions，proposed a mayfly algorithm based on good-point and Lévy flight（JLMA）．The algorithm first adopts good-point set initialization instead of random initialization to increase the traversal of the initial population．Then modifies the position update formula of male mayflies to eliminate the influence of the velocity term on the convergence speed．And finally uses Lévy flight to change the moving direction of male mayfly positions to prevent the algorithm from falling into local optimum．Our experiments on 12 test functions show that the JLMA algorithm can jump out of the local optimum，improve the accuracy of the solution，and have a better result in finding the optimum.

mayfly algorithm；good-point set；Lévy flight

1007-9831（2022）03-0036-07

TP18

A

10.3969/j.issn.1007-9831.2022.03.008

2021-12-16

江西省教育厅科技项目（GJJ201814，GJJ211823，GJJ211825）；江西省2021年大学生创新创业训练计划项目（s202111843031，s202111843039）；九江学院2021年大学生创新创业训练计划项目（x202111843141，x202111843144，x202111843150）

吴霄（2001-），男，江西赣州人，在读本科生．E-mail：2302437854@qq.com

江海新（1980-），男，山东泰安人，讲师，从事智能优化算法研究．E-mail：jianghaixn@163.com