工业场景下基于深度学习的时序预测方法及应用

李潇睿，班晓娟✉，袁兆麟，乔浩然

1) 北京科技大学北京材料基因工程高精尖创新中心，北京 100083 2) 北京科技大学计算机与通信工程学院，北京 100083 3) 北京科技大学材料领域知识工程北京市重点实验室，北京 100083 4) 北京科技大学人工智能研究院，北京 100083

从工业生产过程提取数据特征及领域知识，对复杂系统的运行规律实现可靠建模和状态估计，是提升工业自动化水平的必由之路.在大数据技术、深度学习方法普及前，研究人员常通过机理分析方法、基于物理模型的数值模拟等方法实现数据分析.该类方法虽有良好的可解释性，但需要的理论研究和实验数据较多，当相关变量间存在错综复杂的非线性耦合关系时，工业过程的可靠分析是一项颇具挑战性的任务.从学术和工业的角度来看，了解基础理论和典型工业应用，在利用大数据技术解决工业落地问题中缺一不可，本文将在其余部分进一步介绍.

本文从工业中的时序预测问题出发，针对如何利用深度学习时间序列预测方法促进工业决策水平这一基本动机，介绍了一些经典的和新兴的时间序列预测算法和评估指标，并对工业时序公共数据集、热点工业预测问题进行了综述，最后指出了当前时序预测算法在工业领域所面临的稳健性和可解释性挑战，并探讨了未来的研究方向.

1 时间序列预测算法

随着传感器、过程控制系统等大数据技术的发展，存储、分析海量生产数据成为了可能，基于统计学的传统机理建模方法难以处理工业环境下参数复杂、耦合度高、变化频繁的问题，而深度神经网络面对海量数据时因其绝佳的非线性拟合能力、强大的多模态融合能力，被广泛应用于流程工业中[1]，解决工业时间序列中广泛存在的长时延、高噪音、采样不均匀问题.图1 展示了大数据时代工业决策、生产优化的典型路径，也是本文的核心路线.

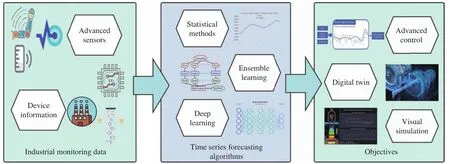
图1 工业生产优化的技术路线Fig.1 Technical route of industrial production optimization

离散时间步下的时间序列预测问题通常给定过去一段时间的目标量与外因输入变量的观测值以及静态环境参数，预测未来一段时间的目标值，可用如式(1)表示：

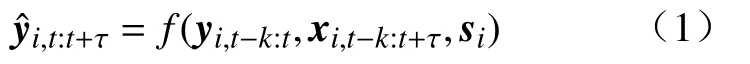
时序预测算法可分为经典统计学算法、集成学习算法和深度学习算法.经典统计学算法采用序列分解或微分思想，使用加性、积分或频域模型将原序列分解为多个子序列，线性构建形如Y=βX+ε的函数，其中 ε为随机噪声.该方法拟合求得的数学函数含义清晰，可解释性强，但忽视了协变量与被预测变量之间可能存在的复杂非线性关系，对复杂过程的表征能力很弱.这类方法被广泛运用于平稳线性时间序列的建模[2]，如转炉炼钢中的碳含量预测[3].集成学习算法结合了统计方法与决策树的优点，串行使用多个弱分类器逼近预测目标.相较于统计学算法，集成学习算法在具有丰富的专家特征选择经验时，使用较少的参数量即可在稠密的多元时序数据上表现出良好的泛化能力.但当数据集具有稀疏、维度较高等特性时，学习效果不如神经网络模型.深度学习方法依托于神经网络强大的非线性表达能力，能够建模复杂系统中预测输出的条件概率分布，更适用于处理大数据量以及多模态输入，在很多场景下获得了更好的预测精度和泛化性能.因此，近年来成为时序预测领域的研究热点.实践中应根据应用场景选择合适的预测算法，具体算法特性对比如表1所示.

表1 时间序列预测算法对比Table 1 Comparison of time series forecasting algorithms

1.1 基于深度学习的时序预测方法

1.1.1 基于循环神经网络的时序预测

循环神经网络(Recurrent neural network, RNN)方法被广泛地应用于序列特征提取上，特别是自然语言处理和时间序列任务.从信号处理的角度，RNN单元可以等效为IIR(Infinite impulse response)滤波器的非线性版本，RNN模型的基本形式如式(2)所示：

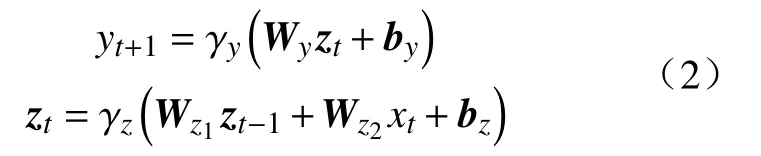
其中,γz(.)、γy(.)表示激活函数，W、b代表参数矩阵和参数向量，z代表隐藏层向量，xt和yt+1代表模型的输入和输出.但由于 RNN存在梯度消失问题，可利用的历史数据非常有限，因此一般采用长短时记忆单元(Long short-term memory, LSTM)处理长时依赖问题.2014年Chung等[4]设计了GRU单元，其在参数量少于LSTM的情况下获得了相似的性能表现，常作为基础网络单元嵌入更复杂的网络结构中，实现对序列信息的有效提取.

一些复杂系统的观测空间和系统的先验知识经常是不完备的，许多时间序列不仅包含了可观测变量，还包括一些潜在的不可观测变量.同时某些时间序列本身就服从某一随机过程.在预测不完备观测空间或带有系统随机性的时间序列时，为了对被预测序列的不确定性进行度量，许多研究者将神经网络的“点预测”替换为“概率分布预测”或“分位数预测”.如2019年Amazon的Salinas等[5]设计了一种基于自回归循环神经网络的方法(DeepAR)，假设待预测的随机变量服从高斯分布，将RNN的每个时间步输出用全连接层投影为两个参数，代表均值和方差，进而支持采样预测以及计算目标值的分位数、期望.但DeepAR方法存在两个缺陷：首先，由于预测时采用了自回归的RNN网络，预测时迭代地对预测值进行祖先采样，使得预测误差存在累积效应，并且无法处理系统的外部观测变量仅在训练时可用、预测时未知的情况.因此也有研究者基于Encoder-Decoder模型，使用非自回归的多步生成方法改进模型的预测效果[6].

1.1.2 基于卷积神经网络的时序预测

卷积神经网络(Convolutional neural network,CNN)因良好的局部特征提取能力而被广泛地应用于图像分析领域.与之相对的，一般认为由于语音、文本等任务的信息密度远大于图像且长度不定，RNN类方法针对序列内部的时序特性进行设计，且具有变长序列信息捕捉能力，因此循环架构是大多数序列建模任务的通用选择.DeepMind团队的Oord等提出的WaveNet[7]改变了这一观点，其使用因果卷积、逐层跳连等方法，将CNN网络用于语音信号的生成.Bai等[8]提出的TCN(Temporal convolutional network)通过使用残差结构和去除门控机制等手段进一步拓宽了WaveNet的使用领域，表现出了比循环神经网络更长的记忆路径，在较少的网络层数下就可获得较大的感受野，对于周期信息具有更强的提取能力.此类方法被广泛应用于有时空特性和图结构的问题中，例如交通流量预测[9-11]，视频动作分割和检测[12-13]等，也有方法将CNN和LSTM结合，利用一维CNN提取特征，LSTM记忆数据相关性，提高预测精度[14].

1.1.3 基于Encoder-Decoder的时序预测

RNN方法的输入输出长度相同，且由于第t时刻的序列输出需要借助t-1时刻的隐状态计算，因此只能使用单步迭代的方法串行完成整个序列的生成，这导致了较高的时间成本和误差累计问题.现实场景中的许多时间序列预测存在要求的输入和输出长度不相等的问题，而RNN的网络结构限制了模型的输入输出长度必须相等.seq2seq(Sequence-to-Sequence)模型具有比RNN模型更强的灵活性，可以实现任意长度的端到端序列预测，是当前工业领域应用中最为广泛的方法[15-16].seq2seq模型将编码器-解码器(Encoder-Decoder)框架应用于序列建模中，包括编码器、隐变量向量、解码器三部分结构，将输入编码为隐变量后再使用解码器生成输出，这种结构使得输入输出均可为任意长度.对于时序问题来说，输入序列往往是历史序列，此时编码器中不存在因果性问题，可以提取所有输入信息后再进行预测，解决了经典RNN网络串行编码使其难以利用完整历史序列信息的问题，但基于RNN的seq2seq仅有一个编码向量，难以包含原始序列中的所有信息，且由于RNN类网络设计导致其对于更近的输入有更高的权重，难以灵活提取不同位置的特征，因此也有很多工作中将seq2seq模型与自注意力机制(Attention mechanisms)结合，进一步增加网络灵活性.

循环神经网络虽具有较强的长时信息处理能力，但对于序列长度在100以上的预测任务来说仍存在传播路径过长、难以学习的问题.自2017年Vaswani等[17]提出Transformer模型以来，此类模型在计算视觉、自然语言处理等多个深度学习领域大放异彩.在编码器和解码器结构中采用Transformer替代循环神经网络，能够在长时预测问题中获得更优的预测精度[18].Transformer的编解码器完全由自注意力机制组成.如图所示，自注意力机制可由式(3)表示：

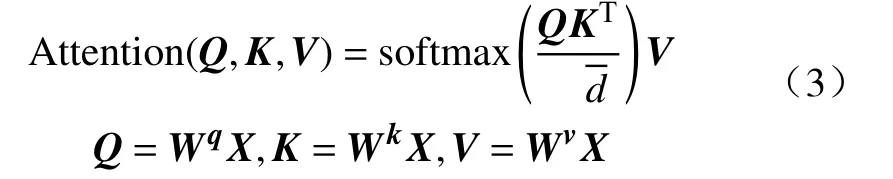
基于全连接网络的自注意力机制使得Transformer有更多的参数和更大的感受野，比CNN网络更灵活，同时解决了RNN、LSTM等序列网络结构存在的难以学习长期依赖的问题，被预测序列中的任意两个位置是等价的.但同时带来了两个问题，一是由于参数量更大，因此需要更大的数据集才能获得较好的训练效果[19]；二是其计算的时间和空间复杂度均为O(L2)，即预测序列长度的平方，因此模型对算力和显存的需求较大，难以解决长序列时序预测问题.

许多围绕通用Transformer的研究工作[20-22]聚焦于使用attention矩阵稀疏化、全局Token等方法降低自注意力所需的计算开销.实现在降低计算复杂度、提升训练速度的同时，提高模型在小数据集下的性能表现.在时序领域许多研究者进行了类似的探索，如Li等[18]借鉴TCN的思路使用因果卷积增强Transformer对局部信息的关注，并设计LogSparse-Attention层将计算复杂度降低到O(L(logL)2)；Zhou等[23]发现使用Transformer学习时序预测任务时，经过softmax之后的权重存在长尾分布特性，因此针对Q矩阵的分布设计了ProbAttention层，将计算复杂度降低到O(LlogL)，有效降低了长序列预测时的显存消耗，并提升了预测性能；Wu等[24]进一步关注到现有端到端的方法未考虑传统时序数据预处理方法中的经典时序分解理论，将序列分解模块嵌入到Transformer中，并使用基于快速傅立叶变换(FFT)的自相关算法，在O(LlogL)复杂度下，实现了序列级的自相关性连接，提升了模型学习序列级特征的能力.

1.2 预测效果评估指标

误差评估指标是预测效果的直观表现，每个统计量只强调了预测序列的某一方面特性，没有某个指标是最佳的.实际任务中应根据数据特性和预测目标选择合适的评估指标[25].对于多元时间序列预测问题，在评价阶段一般针对每一预测变量分别评估，因此本节针对一维预测向量介绍.本文所述的评估指标公式如表2所示，其中Ai表示真实值，表示真实值的平均值，Pi表示预测值，表示预测值的平均值；ei=AiPi表示单点预测误差，n表示序列长度.归一化分位数误差中ρ2(0,1)表示要计算的分位数条件，KL散度中P(.)和Q(.)表示概率分布函数.

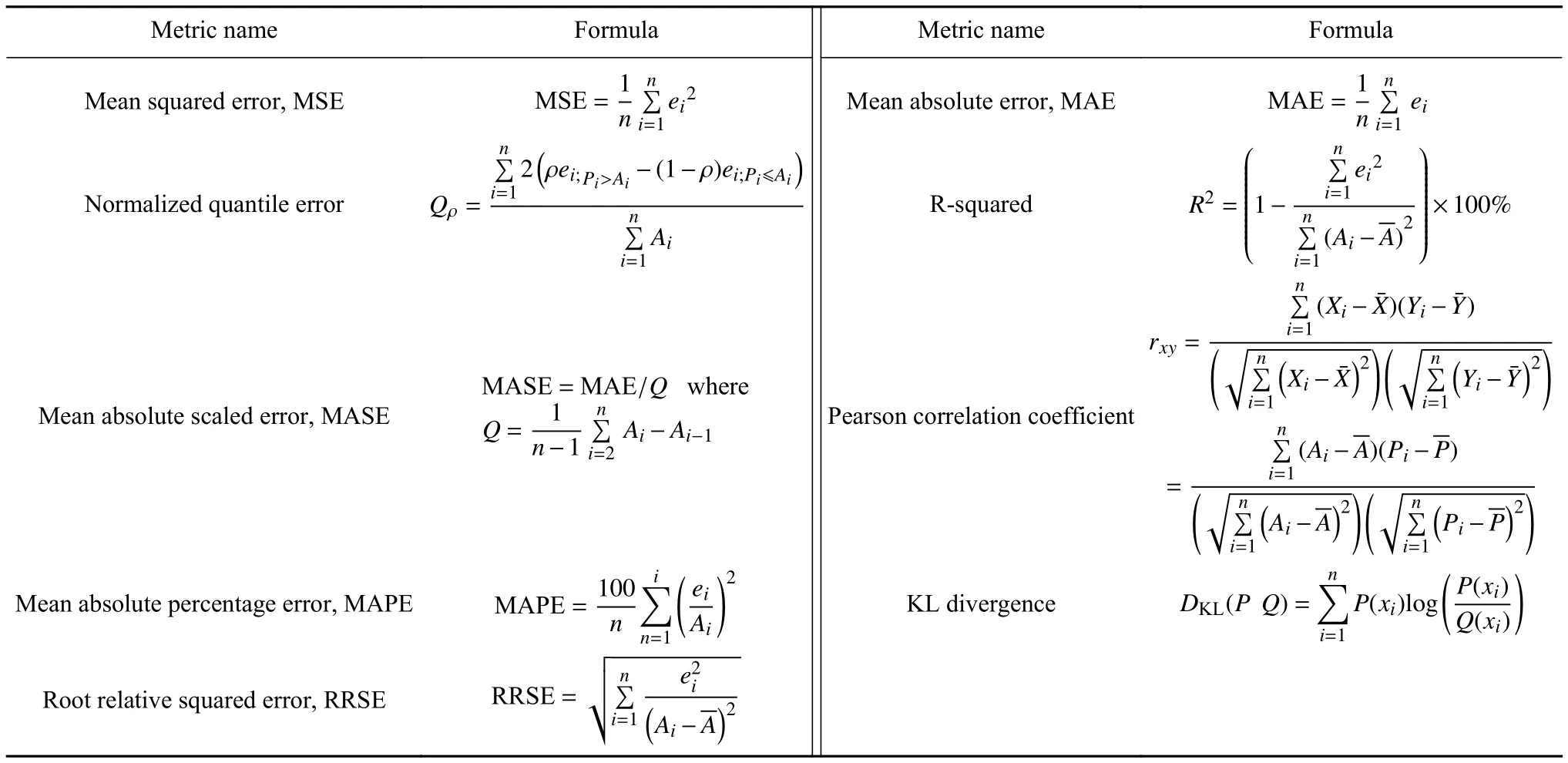
表2 指标定义Table 2 Definitions of the mathematical metrics

在深度学习领域的回归模型中，最常见的误差评估方法是均方误差函数(MSE)，由于其计算简便、数学性质良好的特点，也被广泛用于回归任务的网络损失函数中.但MSE 的量纲与原数值不同，且单点误差对MSE的影响较大.平均绝对误差(MAE)与预测值量纲相同，且降低了对离群点的敏感性，更直观反映预测精度.被预测数据满足标准正态分布时，MSE≥MAE 说明模型预测效果不如均值预测.相比于MSE，RRSE对误差进行了方差归一化，适用于波动剧烈的数据.

当数据不满足标准正态分布时，上述方法不能比较不同数据集的模型预测效果.因此常使用MMAPE、R2和MASE等量纲一的百分比指标比较数据集预测性能.MAPE将预测误差占真实值的百分比作为评估指标；但当真实数据中存在很多0或趋近0的数据时，MAPE的结果可能被严重影响.R2类似于RRSE，取值数据范围为[ -1,100%]，越高代表预测模型的近似效果越好，R2=0为均值预测模型的精度.很多工业问题存在周期性显著，数据变化缓慢的特性，直接使用系统的上一时刻或上一周期的状态作为预测值，即可获得较好的预测性能[26]，此时可使用MASE指标代替R2指标，从对模型绝对误差的评估转变为对数据变化的评估.一些方法将预测目标值问题转换为预测分布及分位数(详见第1.1.1节)，此时可用分位数误差评估预测分布的分位数的准确度.

上述指标仅聚焦于被序列点的预测准确度，未对形状、趋势、周期等序列模式的预测性能进行分析.因此在分析预测结果时，也可以使用Pearson相关系数(PPMCC)、欧氏距离、动态时间归整(Dynamic time warping, DTW)等算法从序列特征的角度量化解释预测效果.

2 工业应用

2.1 工业时序数据集

工业应用生产实验危险度高、监测控制指标多，优秀的工业时序数据集可显著降低算法实验成本，加快算法设计速度.如经典的工业系统辨识领域的数据集DaiSy[27]，该数据库中提供了11种工业过程，包括受控搅拌槽中混合两种物质产生的工艺参数变化，柔性机械臂中加速度与力矩间的关系，钢副车架柔性结构悬挂振动测量等.

近几年的数据集涵盖了更多、更先进的传感器数据，如加利福尼亚大学贡献的机器学习时序数据集[28]，其中包括不同组分的混凝土抗压强度随存放天数变化、气体传感器的零点漂移校准和温度控制、机器故障的预测性维护数据等，并依据数据类型(单变量、多变量)、序列长度及问题类型进行了归类.莫纳什大学对20个热点时间序列数据集做了进一步的整理[29]，包括321户家庭在2012～2014年的小时级用电情况，澳大利亚风力发电厂的产能情况等，使用4种误差指标评估了13种基线方法在所有数据集上的预测效果.

2.2 过程工业

过程工业指以石油化工、冶金采矿、能源电力等原材料为代表的基础加工工业，相较于离散工业，过程工业具有生产连续性高、原材料变化频繁、涉及机理变化复杂、难以使用数学模型精准表达等问题.工艺流程中的存在诸多难以准确测量或实时测量的物料属性、工艺参数等，充分利用大数据和人工智能等信息技术，可以显著提高这些场景下的建模、控制、决策水平.

在工业场景下，已有很多工作使用时间序列分析模型及算法，建模、预测系统的运行过程以解决实际生产问题.本章将以采矿、冶金为例，介绍工业时序预测技术的典型应用案例.

2.2.1 采矿工程领域

大量的深度学习技术已经被用于矿物加工领域，其中最多的是机器视觉技术，因为从图像上提取特征分析矿物关键参数(品位、回收率、磨矿粒度、矿物成分等)的成本显著低于采样或化学分析方法，神经网络技术的成熟也大大提升了此类无接触式分析方法的准确度.另一个重要的领域就是基于工业数据的建模，虽然复杂工业领域往往部署了大量的传感器，但这些传感器更多面对的是容易简单、实时测量的物理量，比如表面流速、压力、温度、密度、功率等，而对于物理化学变化中其他一些关键参数则难以有效的获得，如大型设备内部的难以观测的流量场、温度场、压力场，以及混合物的组分、微粒尺寸分布、材料应力等，一般需要通过实验室实验、半工业实验等手段逐步加深认识[30].在理论研究的基础上，设计深度学习算法建模非线性变量，实现智能监测、智能预警等，此类模型常被称为软测量模型(Soft-sensor model)[31-32].近年来，已有很多基于数据的建模技术[33]应用于工业数据或在工业环境部署.

在采矿领域中，很多工作使用时序预测方法建模生产中使用的工业设备.Núñez等[34]提出了一种基于神经网络的模型预测控制方法，使用RNN网络建模膏体浓密机泥床压力、高度、泥层底流浓度等参数，并依赖于预测结果使用粒子群算法对浓密系统进行控制.Zhang等[35]针对浮游选矿场景下，泡沫视频和锌品位测定的采样频率不同且存在时滞的问题，设计了一种结合多层感知器(MultiLayer perceptron, MLP)和RNN的特征重建回归网络，以充分利用时间不匹配的泡沫视频特征，预测当前浮选品位.Yuan等[36]针对工业过程具备的连续时间特性，提出了以常微分方程网络(ODE-Net) 作为网络骨架的序列预测模型，并有效应用于工业膏体浓密机底流浓度的预测中，在不同预测长度的实验中均获得较好效果.有效的油井产量预测可以延长油井生命周期、提高油品采收率，但传统数值模拟方法需要许多难以获取和计算的地层和流体数据.Fan等[37]尝试使用自回归综合移动平均模型-长短时记忆网络混合模型(ARIMA-LSTM)预测油井生产情况，发现当人工操作较少，序列中的非线性特征不明显时，ARIMA模型对于整体运行趋势有更好的拟合效果，LSTM对非线性波动的学习效果更好，两者结合可以更好地适应生产状况.

2.2.2 冶金工程领域

对于钢铁冶炼等流程制造工业，生产加工过程中涉及多个连续耦合的非线性工序，为保证最终成品的质量，需将各阶段产物的工艺参数限制在规定阈值内，因此需要实时掌握部分关键参数的变化趋势.Zhang等[38]针对高温熔铝回转炉中温度控制不精确、难以保证优品率的问题，设计了一种基于CNN和RNN结合的DCGNet网络，以预测回转炉烧结温度；Li等[39]结合因果卷积与基于GRU的注意力机制实现了对高炉中铁水硅元素含量的预测.

由于工业系统广泛存在的非线性、高时延等特性，利用传统控制技术难以获得精准控制效果，因此部分研究工作将时序预测算法应用于系统控制信号的求解中.如Du等[40]针对贫铁矿烧结过程中的智能控制问题，将时间序列分析方法和模糊控制相结合，使用Hurst指数及Mann-Kendall方法提取烧结过程趋势，根据置信水平划分时间序列阶段，结合专家经验设计模糊控制方法实现了对烧穿点的精确控制.除此之外，该预测控制思想还被应用于浓密机底流浓度控制[41]，炼钢-连铸过程中工件释放时间调度[42]等场景.

2.2.3 其他

许多时序预测研究工作聚焦于解决设备参数预测、产量预测、能耗预测等问题上，以优化排产管理水平，提升经济效益.如Han等[43]使用双向LSTM网络分析预测乙烯产量.Wang等[44]针对离散过程工业中存在的特征序列具有多个相位难以对齐和复杂动力学过程变化频繁的问题，使用LSTM提取每个产品批次中与质量相关的隐藏特征，预测各阶段化学产物质量.Essien等[45]设计了基于ConvLSTM的自编码器，模型使用一维CNN网络提取特征，并输入至LSTM学习序列信息，以实现对高速铝制罐机运行速度的单变量预测，改进生产线上下游设备的调度计划.Antonopoulos等[46]、Zhou等[23]通过预测电网使用率调节发电机组运行功率，以提高能源利用率等.

3 工业应用中的挑战

相较于天气、经济等预测任务来说，工业上的时间序列预测的精度要求相对略低，但对模型的稳健性和可解释性提出了更高的要求.

稳健性表示预测模型在遇到外部扰动或者内部故障时，确保系统表现稳定的能力.对工控系统来说，当预测模型面对未曾学习过的数据分布(如设备故障或物理性质改变)时，模型应仍有良好的泛化性能，可以正确给出预测；即使没有，至少应该能够发出警告，表明因为情况的不寻常导致当前的预测是不可靠的，需要其他系统或人工介入.

从关注者的角度，可解释性可分为对开发者和对使用者的可解释方法[47].工业中的可解释性更侧重对使用者有意义.开发者更希望借助可解释性关注某结构对模型预测结果的影响，以及模型预测正确或错误的原因.而使用者不看重模型的具体构成元素，更侧重模型从系统输入到输出的数学映射，了解系统对于不同的输入可能做出的反应；他们不是深度学习的专家，但需要保证融合了深度学习的系统可以正常工作.

3.1 稳健性

工业系统中，数据量通常较为充足，但时常质量不佳.首先，受限于网络通信质量和不同设备动作时刻差异，传感器采集的数据大多存在缺失或非均匀采样的情况.在实际使用时，须预先对数据进行采样或插值工作.其次，过程工业中的多个传感器可能拥有不同的采样频率，此时使用线性插值方法可能带来较大信息损失，因此应预先确定好统一的采样周期，或使用生成式的方法实现多采样率的生成.Demeester[48]提出采用具有时间感知的连续时间模型ODE网络学习常微分方程，从而实现对非均匀时间序列进行的直接建模，也有研究者使用Kalman滤波方法在线融合多采样率数据[49]等.

将模型预测结果展现给决策者时，需要考虑模型的稳健性.传感器和工业设备都可能出现设备老化、零点漂移等问题，模型应及时发现并给出提示，通知技术人员按时校准或更换，因此很多工作研究了如何在线检测数据的异常波动.例如，Martí等[50]使用支持向量机算法检测不符合有效传感器信号模型的数据；Malhotra等[51]使用基于LSTM的自编码器模型检测序列异常，对无周期性的或存在高随机性的复杂长序列，该方法仍具有较好的鲁棒性.

3.2 可解释性

深度学习的可解释性可分为局部和全局可解释，局部是基于样本的解释，通过数据集的部分样本解释模型行为；全局是基于结构的解释，对于整体方法或数据集均成立；在关注点上，可分为时间和空间的可解释性，前者即某变量过去每个时刻对于预测的重要性程度，后者即每个输入变量对预测影响的重要性程度.

为提高模型设计者对模型性能的了解，研究者针对各种深度时序预测算法的可解释性进行研究，以分析模型参数与输出间的联系.Siddiqui等[52]通过计算每一层CNN网络对输入的偏导获得神经元对于输入的激活程度，激活值越高反映出该位置对预测的影响更显著；Schockaert等[53]针对使用LSTM模型预测高炉铁水温度的可解释性进行分析，将Attention机制嵌入LSTM中并对其参数可视化实现了对预测的全局时间可解释，并在输入层加入CNN使用导向反向传播(Guidedbackpropagation)方法获得输入变量对全局空间可解释性，提升了铁水温度建模的准确度和解释性水平.

除对模型内部的可解释分析外，另一类可解释方法称为外部协同的解释(External co-explanation)，其将神经网络视为黑箱模型，直接分析特征输入和输出间的联系.LIME(Local interpretable modelagnostic explanations) 模型[54]假设特征分布是连续且线性的，此时通过对某样本施加扰动，可获得该样本附近的特征分界，进而了解不同特征对该样本预测的贡献.Lundberg等[55]利用Shapley值法从博弈论角度建立加性模型框架，避免了LIME中对局部精度和一致性的破坏.以上方法已被广泛地应用到工业场景下模型的特征解释与分析中，如在套管试验台的疲劳实验中筛选特征以提高使用寿命[56]，建模家庭特征与电力使用情况[46]等.

4 结论与未来的工作

未来的研究方向包括以下几个方面：

（1）传统统计学方法具有良好的可解释性和抗噪性，深度学习方法对高维和非线性问题有强大的拟合能力，将两者结合有可能增强模型预测效果和可解释性.

（2）Transformer在短期和周期性预测问题上取得了良好效果，但是受限于复杂度，该方法在长序列预测问题中仍有较大应用瓶颈.目前存在使用局部敏感哈希、概率注意力降低时空复杂度的方法，但利用周期、趋势等时间序列独有的特征，借鉴频域处理等方法设计网络，以增强网络的归纳偏置进而提高性能的工作较少，尚待进一步探索.

（3）相比于零售业、天气预测问题，工业数据广泛存在着时延长、周期性弱、变量数量多、采样不均匀、传感器高噪音等问题，目前也涌现出了可学习的位置编码、表示学习、基于微分方程网络的模型等相关理论研究，如何将此类研究与实际结合，是未来的热点问题.

（4）工业环境下，时间序列数据往往来源于已经具有理论研究的工业设备或系统，如何有效地利用专家知识，将已知的系统特性嵌入网络设计环节，仍是一个值得深入研究的问题.

大数据技术的普及使得数据驱动方法在新一代智慧工厂建设中发挥着举足轻重的作用，而深度学习技术凭借强大的非线性表示和特征学习能力，在流程工业建模和数字化过程中得到了广泛的应用.本文针对深度学习技术在复杂流程工业，特别是采矿冶金行业中的时间序列预测问题，围绕模型算法、评估指标、应用现状、未来挑战四个方面进行了概述，总结了深度学习方法的发展脉络，指明了近期的发展热点，并结合工业需要对评估指标和方法的稳健性和解释性要求做了进一步说明，助力深度学习方法落地于更多的工业场景，进一步提升工业生产的智能化水平.