基于多目标多约束条件下排产算法设计与应用＊

罗小峰 胡 莹 余 翔

（①南昌大学机电工程学院，江西 南昌 330031；②中国联合网络通信有限公司江西省分公司，江西 南昌 330006）

随着网络信息化的发展，MES 系统逐步进入生产车间。生产规模扩大，对实际生产适应度要求变高。离散型的车间调度[1]问题，多品种小批量的生产需求，多目标、多约束[2]条件的实际场景，让求解过程愈加复杂。

国内外学者对排程问题进行了深入研究与分析。目前用于解决该类问题的方法有量子遗传算法、粒子群优化算法和人工蜂群算法等[3-5]。LI S Y 等[4]提出了一种粒子群优化算法，专注于收敛性的速度和质量；Kamal A M 等[6]总结前人研究成果，为后人的研究提供了参数指导和研究方向；针对收敛速度慢问题，Mohit A 等[7]在粒子群算法的基础上结合遗传算法提出了新颖的元启发式技术；王玉芳等[8]将遗传算法与模拟退火算法结合，提升算法寻优能力；为保留父代优良特征，张超勇等[9]提出新的POX 交叉算子，荆巍巍等[10]对于多目标调度问题提出自适应NSGA-II 算法，并通过实例证明了算法有效性。以上研究提出了许多算法模型，算法之间的结合方便了问题的求解。由于APS 本身适用性不强，目前在实际生产中的应用并不理想，因此本文基于某机加车间的实际生产情况，提出了基于传统遗传算法，解决多目标、多约束条件生产排程问题的改进遗传算法，建立相关排产模型并求解，提高生产排程效率。

1 问题描述与建模

1.1 问题描述

APS(advanced scheduling)排程是一种基于有限产能的特殊排序方式，即在某一段时间将工序、设备和人员分配到对应时间节点上，最终达到高效有序生产的目的。

订单是整个生产车间的核心，根据生产需求分析后可以得出生产任务。设备之间存在产能差异，产品可能存在多工艺路线，还存在双工位情况，即一台机床，可以同时加工两道工序。

企业生产效率要提高，关键在于降成本、降废品率，提高设备利用率，减少设备空闲时间。排程中所涉及的要素如表1 所示。

表1 机加排程问题信息

1.2 约束条件

（1）设备存在双工位交替的情况，即同一设备、两个工位，同时作业。

（2）单个零件加工时间只受设备生产节拍影响，即设备的产能一定。

（3）如设备中途出现故障，更换设备的时间忽略不计。

（4）相邻设备优先派工，根据设备的派工优先级进行派工。

（5）同一种零件优先安排在同一台设备上进行加工。

（6）工序委外需等该工序完成后才能开始下一道序。

（7）交期靠前的订单优先安排生产。

约束条件的多元性，决定了算法设计的复杂度，其中双工位需考虑交替加工情况，保证工序不发生混乱。相邻设备在空闲时考虑优先派工，缩短物料运送时间，设备的派工优先级还需根据使用频次动态调整，提升设备使用率。

1.3 目标函数

（1）按时交货因子，保证在交货期之前完成订单。

（2）48 h 达成率因子，即相邻两序之间加工间隔时长不超过48 h。

（3）设备连续性影响因子，尽可能缩短设备待机时间，提高设备使用的连续性。

（4）最短完工时间影响因子，即尽早完成生产任务。

以上的生产排程目标，涉及到众多影响因素，彼此间存在矛盾关系，往往难以兼顾所有，需均衡各方面要素。

1.4 数学模型

根据以上问题的描述与分析，本文采用加权组合优化法，建立如下目标函数模型：

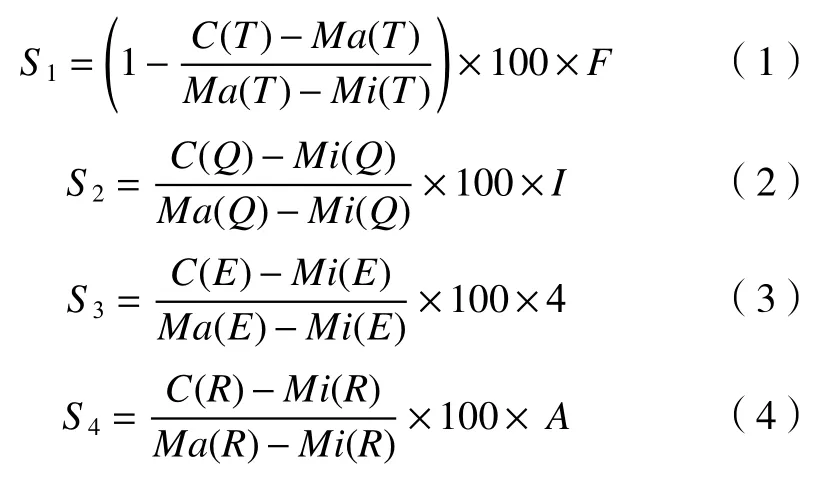
其中：C(T)为工序结束时间，Ma(T)为工序结束最晚时间，Mi(T)为工序结束最早时间。C(Q)为按时交货数量，Ma(Q)为按时交货的最大数量，Mi(Q)为按时交货的最小数量。C(E)为连续设备数量，Ma(E)为连续设备的最大数量，Mi(E)为连续设备的最小数量。C(R)为48 h 达成率数量，Ma(R)为48 h 达成率最大数量，Mi(R)为48 h 达成率最小数量，以上时间都按分钟计算，F为是否完成比率，I为是否按时完成比率，A为是否达成比率。

式中：S1为最短完工时间影响因子；S2为按时交货影响因子；S3为48 h 达成率影响因子；S4为设备连续性影响因子；W1为最短完工时间影响因子权重；W2为按时交货影响因子权重；W3为48 h 达成率影响因子权重；W4为设备连续性影响因子权重。

2 算法设计与优化

2.1 算法设计

运用遗传算法的思想，将实际生产与理论相结合，更好地解决实际问题。将众多排产方案看作一个种群，一个排产方案对应一条染色体，工序对应基因，考虑到实际生产中还有设备元素和双工位的情况，引入分子和裂变分子的概念，一台设备对应一个分子，如果是双工位，则存在裂变分子。

2.1.1 编码

合适的编码方式使得算法求解变容易。机加生产中的排程问题，首先确定加工路线，之后是设备分配，最后是人员排班。

通过分析，采用三段式排程编码方案，第一段为工序分配，即确定工序的总时长、开始时间和结束时间，计算公式如下：

其中：Ri为第i道序的节拍，Li为加工的数量，Si为加工时长，Tie为结束时间，Tis为开始时间。T总为总时长，S为工序集合{S1,S2,···,Sn}。

第二段为设备分配，确定加工零件的设备工作时段，计算公式如下所示：

其中：Mie为设备结束时间，MiS为设备开始时间，M总为所有设备总加工时长，M为设备集合{M1,M2,···,Mn}。

第三段为人员分配，确定相关操作人员工作时段，计算公式如下：

其中：Gie为操作人员结束时间；GiS为操作人员开始时间；G总为所有操作人员总加工时长；G为人员的集合{G1,G2,···,Gn}。

例如F1(S1,M2,G1)为任务F1的第一道工序由G1人员在M2设备上进行加工。

2.1.2 初始染色体种群

种群规模大小的选择关系到排程结果的好坏，一般选择种群大小在[50,200]。

采用加权系数法生成初始种群。对于插单的情况需采用前向排程,给突发情况留更多的缓冲空间，保证交货期之前完成任务。对于委外工序，即该工序外包生产，采用前、后混合排程，在委外工序完成之前采用后向排程,在委外工序完成之后采用前向排程，有利于前后工序的紧密衔接。而对于以按时交货为目标的任务，采用后向排程，保证按时交货的同时降低库存成本。

按照一定的权重随机生成初始种群，面对不同的排程任务，动态调整权重大小。

2.1.3 选择、交叉和变异

个体适应度越大，排程结果越优，根据个体的好坏程度决定个体选择的概率，极大程度避免优良个体交叉变异之后成为较差个体，一定程度上保证了算法的收敛速度，也被称为保优策略。一般选择概率在[5%,10%]，本文选取8%，这部分个体直接进入子代种群中。

交叉是遗传算法中的关键步骤，通过染色体交叉操作，可产生优良品种，增加种群多样性。由于工序交叉无法保证产品的正常生产，所以采用设备两点交叉的方式，即随机设置两个交叉点，再进行部分基因交换的方法。一般交叉概率在[50%,90%]。本文采用动态交叉概率，在交叉过程中，不断改变交叉因子的大小，具体计算如下：

其中：Xi为交叉因子；G为总迭代次数；g为当前迭代次数。

采用均匀变异的方式，在符合某一范围内取随机数，这一变异方式适合于种群的初始运算。变异因子随迭代次数动态变化。具体计算如下：

其中：Qi为变异因子；G为总迭代次数；g为当前迭代次数。

通过非固定交叉因子和变异因子，避免陷入局部最优解的同时，加快收敛速度，一定程度上提升了计算效率。

2.2 算法优化

基于遗传算法的思想，在以下几方面优化排产结果：

（1）基于产能失衡，或工序阻塞问题，在初始化种群时，根据派工级别按动态概率选择设备。首先随机产生索引数组（一个个数小于最大数的索引数组），索引数字大的概率高。

比如：index=4 产生的概率分布输入：1-1/10,2-2/10,3-3/10,4-4/10。计算平均最优时间，将生产任务分派到设备上，保证设备分派的优先性和均衡性，计算公式如下：

其中：P总为计划生产总数；T为平均时间；R为节拍；H为已占用时间。

（2）针对双工位的设备，提出裂变分子的概念，算法设计伪代码如下：

在排程结果涉及双工位设备时进行染色体偏移，调整工序之间的空隙，提高排程的紧凑性，算法设计伪代码如下：

（3）针对排程任务多造成速度慢，效率低问题，采用工序合并降低订单数量，算法设计伪代码如下：

3 结果分析

3.1 实例描述

本文以某机械制造公司的实际生产排程为例，利用所设计的算法求解，算例中涉及8 种零件，共1 255 个产品，50 台相关设备，其中2 台双工位设备，9 条加工路线，1 个零件是双工艺路线，表2为各工序可选设备，表3 为每台设备单位生产节拍。

表2 工序可选设备

表3 设备单位生产节拍

3.2 排程展示

本文算法基于.NET 平台，采用B/S 架构实现客户端开发。排产过程运行在Window10 专业版64 位操作系统的PC 端，12.0 GB 运行内存，i7-5500U 双核四线程处理器，最后经过6.3 s 得出结果。各参数详细说明如下：

最短完工时间权重W1=0.3，按时交货权重W2=0.4，48 h 达成率权W3=0.2，设备连续性权重W4=0.1，初始种群大小200，最大迭代次数150，选择概率0.08，初始交叉概率0.8，变异概率0.05。

排程结果如图1 所示。

对比之下，改进后的遗传算法效率大大提高，产能充分利用，稳定性有保证，排程结果更加紧凑，设备使用率变高，加工时间缩短，人员安排更加灵活。

以传统遗传算法排程为1，两种排程方式性能对比结果如表4 所示。

表4 结果对比

从表4 中数据可看出，改进排程在排产速度方面大大提高，经过多次排程性能均相差无几，稳定性好，在处理多目标、订单种类多和动态排程的情况，改进后的排程系统优势更加显著。

4 结语

本文基于多约束，多目标条件下的机加生产排程问题，设计多目标优化模型，利用加权系数组合优化法均衡各目标，采用三段式排程编码方案进行编码，在传统遗传算法的基础上进行改进，设计了分子和裂变分子模型，针对裂变分子提出染色体偏移求解方法，保证了初始解质量。通过动态调整交叉和变异因子大小，弥补传统算法收敛速度慢的缺陷，相较于传统遗传算法排程优势明显，为多约束多目标条件下的离散型机加生产制造提供理论指导。由于本文在算法设计上不够简洁，且未将成本因素考虑在内，这将作为今后进一步研究的方向。