Deep convolutional adversarial graph autoencoder using positive pointwise mutual information for graph embedding①
MA Xiuhui (马秀慧), WANG Rong, CHEN Shudong②, DU Rong,ZHU Danyang, ZHAO Hua
(*University of Chinese Academy of Sciences, Beijing 100049, P.R.China)
(**Institute of Microelectronics of the Chinese Academy of Sciences, Beijing 100029, P.R.China)
(***Key Laboratory of Space Object Measurement Department, Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, P.R.China)
Abstract Graph embedding aims to map the high-dimensional nodes to a low-dimensional space and learns the graph relationship from its latent representations. Most existing graph embedding methods focus on the topological structure of graph data, but ignore the semantic information of graph data,which results in the unsatisfied performance in practical applications. To overcome the problem, this paper proposes a novel deep convolutional adversarial graph autoencoder (GAE) model. To embed the semantic information between nodes in the graph data, the random walk strategy is first used to construct the positive pointwise mutual information (PPMI) matrix, then, graph convolutional network (GCN) is employed to encode the PPMI matrix and node content into the latent representation.Finally, the learned latent representation is used to reconstruct the topological structure of the graph data by decoder. Furthermore, the deep convolutional adversarial training algorithm is introduced to make the learned latent representation conform to the prior distribution better. The state-of-the-art experimental results on the graph data validate the effectiveness of the proposed model in the link prediction, node clustering and graph visualization tasks for three standard datasets, Cora, Citeseer and Pubmed.
Key words: graph autoencoder (GAE), positive pointwise mutual information (PPMI), deep convolutional generative adversarial network (DCGAN), graph convolutional network (GCN), semantic information
0 Introduction
Graph data has been widely used in various areas,including social media, e-commence, citation networks and protein-protein interaction networks. Analyzing the graph data has become a hot topic of current researches, such as link prediction[1], node classification[2], node clustering[3]and graph visualization[4].However, the irregularity and complexity of graph data lead to the high computational complexity and low parallelism, which brings great challenges to existing graph data researches.
Graph embedding maps the complex graph data into the latent and low-dimensional feature representations, meanwhile it captures the network topological structure, vertex content, and other information of graph data, which facilitates the processing and analysis of graph data. With the graph embedding, traditional pattern recognition models (e.g., linear support vector machine (SVM)) can easily achieve graph analysis tasks (e. g., classification tasks). Motivated by this advantage, many improvement studies have been proposed[5-6].
In recent years, graph autoencoder (GAE)[7]combined with graph convolutional network (GCN)[2]has received more and more attention. Graph autoencoder employs GCN[2]to encode the node structure information and node feature information at the same time. Since the distribution of latent representations learned by simple GAE[7]has no restriction, which results in the poor embeddings. The variational graph autoencoder (VGAE)[7]applies Gaussian prior to learn the distribution of the latent representation, which greatly improves the effectiveness of the latent representation. The adversarially regularized graph autoencoder (ARGA)[8]uses the generative adversarial network (GAN)[9]to enforce the latent code to approximate the prior distribution. Although these graph autoencoder models make full use of the structural information of graph data,they ignore the semantic information between nodes.
In this paper, a novel graph autoencoder model is proposed to capture the semantic information between nodes. The proposed model firstly constructs the postive pointwise mutual information (PPMI) matrix[10]through the random walk strategy[11], which learns the semantic information between nodes of the graph data.Then GCN[2]is employed to encode the PPMI matrix and node content of the graph into the latent representation. Finally, the decoder is used to reconstruct the topological structure of the graph data based on the learned latent representation. To further enhance the robustness of graph representation, this work introduces the deep convolutional adversarial training scheme to regularize the latent code. The purpose of the deep convolutional adversarial training module is to distinguish whether the latent code comes from the real prior distribution or from the graph encoder. In the unified framework, graph embedding learning and deep convolutional adversarial regularization are jointly optimized to benefit each other and eventually get better graph embedding. The experimental results on the benchmark datasets prove that the proposed algorithm shows the good performance on link prediction, node clustering and graph visualization tasks. The contribution of this paper can be summarized as follows.
A novel deep convolutional adversarial graph autoencoder model using positive pointwise mutual information is proposed.
The PPMI matrix and node content of the graph data are encoded into a latent and low-dimensional representation, which better captures the semantic information of graph data.
Deep convolutional adversarial regularized framework is used to further match the learned latent code to the prior distribution.
The network structure of the existing graph autoencoder is changed. The adjacency matrix is replaced by the PPMI matrix as the input of the autoencoder to reconstruct the graph structure.
1 Related work
DeepWalk[4]extends language modeling techniques from word sequences to paths in the graph,which uses the random walk strategy to learn the graph embedding. In this work, they treat the nodes obtained from the random walk strategy as context nodes. Since then, a number of probabilistic models have been proposed including LIKE[12], node2vec[13]and so on.Ref.[14] further extended DeepWalk[4]to encode the multi-scale node relationships in the graph. These methods mentioned above embed the graph data base on the random walk strategy, and they assume that the nodes are similar if they are close to each other in simulated random walks over the graph. However, these methods are only suitable to shallow models, which cannot capture the complex graph structure.
In recent years,deep learning networks are widely used for graph embedding, which can greatly explore the nonlinear graph structures. SDNEI[15]used stacked autoencoder to jointly preserve the first and second-order proximities of nodes in the graph. DNGR[16]exploited the stacked denoising autoencoder to reconstruct the PPMI matrix. But these methods only consider the topological structure information of the graph and fail to consider the content information of the nodes. GCN[2]embedded both the topological structure information of the graph and the feature information of the nodes,which greatly improves the performance of the graph networks on various graph tasks. Ref.[7] proposed GAE which uses GCN[2]as the encoder to reconstruct the adjacency matrix of the graph. To further enforce the latent representation to approximate the prior distribution, Ref.[8] proposed ARGA which employs the training scheme of GAN[9]. However, ARGA[8]ignores the semantic information. Inspired by this, the PPMI matrix and node content information of the graph are embedded in the encoder to capture the semantic information between nodes. Meanwhile, deep convolutional generative adversarial network (DCGAN)[17]applies convolutional layers to generative adversarial network, which greatly improves the stability of GAN[9]training and the quality of generated results. Motivated by this,a deep convolutional adversarial training scheme is incorporated to learn a more robust graph representation.
2 Problem definition and framework
2.1 Problem definition
This paper firstly defines some commonly used symbols to represent the graph structure and then presents the unsupervised representation learning problem of the nodes on the graphG.
G= {V,E,X} is used to represent an undirected graph, whereV= {v1,…,vN} means the set of nodes andNis the number of nodes.Edenotes the set of edges, whereeij∈Erepresents the edge between the nodeviand the nodevj. In addition, the adjacency matrixA∈R N×Nis used to represent the topological structure of the graphG, whereAij=1 ifeij∈E, otherwiseAij=0.AndX∈R N×Mmeans the feature matrix of the nodes, wherexi∈R Mcorresponds to theith row of matrixX, denoting the feature of nodevi, andMis the dimension of the feature.
Given a graphG, the goal is to learn the low-dimensional representationZ∈R N×Dof the nodes in the graph, wherezi∈R Drepresents the D-dimensional representation of the nodevi, andD<<N. It is hoped thatZas an embedded matrix can capture not only the content information and topology information but also the semantic information of nodes.
2.2 Overall framework
The framework (DCAG-AE) consists of three main parts: constructing PPMI matrix by the random walk strategy, graph autoencoder, and the deep convolutional adversarial network. Fig.1 briefly displays the workflow of DCAG-AE.
Constructing PPMI matrix On the basis of the topological structureAof the graph, this work constructs the PPMI matrix with the random walk strategy.
Graph convolutional autoencoder The encoder encodes the PPMI matrix and the node contentXinto a latent representationZ, and then the decoder reconstructs the topological structureAon the basis ofZ.
Deep convolutional adversarial regularization
The deep convolutional adversarial network trains a discriminator to discriminate whetherzi∈Zcomes from the encoder or the prior distribution, which further enhances the robustness of the encoder.
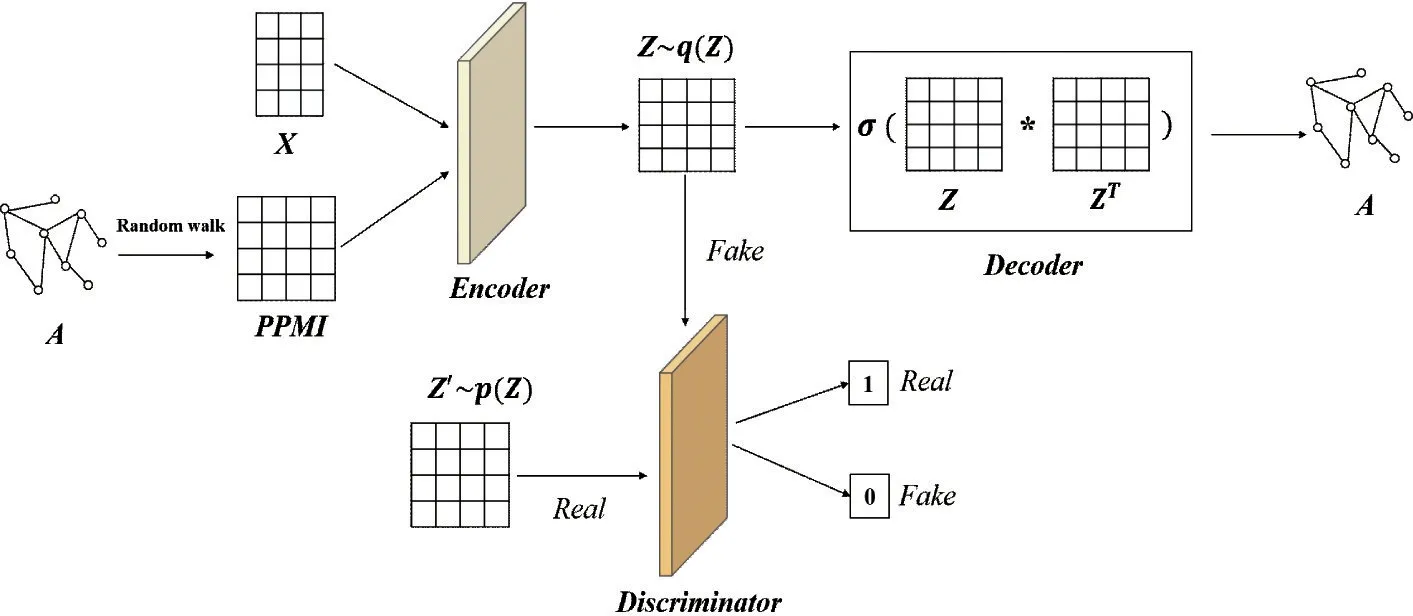
Fig.1 The brief architecture of the deep convolutional adversarial graph autoencoder using positive pointwise mutual information for graph embedding (DCAG-AE). Top half of the network corresponds to the graph convolutional autoencoder which exploits the PPMI matrix and node content X to reconstruct the topological structure A. Bottom half is a deep convolutional adversarial network, which discriminates whether a sample comes from the encoder or the prior distribution
3 Proposed model
3.1 Constructing PPMI matrix
Motivated by DGCN[18], which uses the random walk strategy to construct the PPMI matrix for the graph nodes classification task. Specifically, with the topological structureA, this paper firstly exploits the random walk strategy to build a co-occurrence matrixC∈R N×Nof nodes on the entire graph. Then, according to the matrixC, this paper constructs the PPMI matrix and explains how to capture the semantic information between nodes of the graphG.
Constructing nodes co-occurrence matrixC.DeepWalk[4]proves that in the connected graph, the degree of nodes and the frequency of nodes in the short random walk conform to the same distribution. So, in this work, the short random walk strategy is used to construct the nodes co-occurrence matrixC.
Algorithm 1 shows the construction process of nodes co-occurrence matrixC. First,randomly select a nodev1from the graph as the current node, then a nodev2is randomly selected from the neighbors of the current node and is made as the new current node. Repeating this random sampling process to obtain a random walk sequenceTuntil the number of nodes in the sequence reaches the walk lengths. Then sample the node pairs (va,vb) from the sequenceTuniformly,and add 1.0 to the value ofCa,bandCb,ain the matrixC. Finally repeat the above processγtimes which is called the total walk. Note that the probability of reaching any of its neighbors from the current node in the algorithm is equal.

Algorithm 1 Construct nodes co-occurrence matrix C Input:graph G = {V, E, X} with adjacency matrix A;window size w;walks per node γ ;walk length s;Output: the nodes co-occurrence matrix C∈R N×N;1. Initialization: initialize the matrix C∈R N×N to 0;2. for i=0 to γ do 3. O = Shuffle (V);4. for each vi∈O do 5. T =RandomWalk (A, vi, s);6. Uniformly sample all node pairs (va, vb)∈T within w;7. for each pair (va, vb) do 8. Ca,b + =1.0;9. Cb,a + =1.0;10. end for 11. end for 12. end for 13. return nodes co-occurrence matrix C.
Constructing PPMI matrix. Based on the nodes co-occurrence matrixC, the PPMI matrix is calculated as
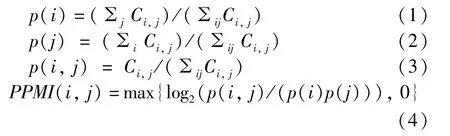
wherep(i) is the probability that nodeviappears,p(j) is the probability that contextcjappears,p(i,j)is the probability that nodeviand contextcjappear at the same time.
It can be seen from the calculation formula of the PPMI matrix that when the nodeviand the contextcjare independent,p(i,j) =p(i)p(j), thusPPMI(i,j) =0.When the nodeviand the contextcjare related, i.e.,p(i,j) >p(i)p(j), that isPPMI(i,j) >0.Furthermore, the higher the correlation between the nodeviand the contextcj, the greater the value ofPPMI(i,j). Therefore, PPMI matrix can capture the semantic information between the node and its context nodes,which is not captured by the adjacent matrixA.Additionally,when calculating the nodes co-occurrence matrixCusing the random walk strategy, the PPMI matrix not only captures the information of the first-order neighbor nodes, but also is associated with higherorder neighbor nodes. That means the PPMI matrix can mine more potential relationships between the nodes.
Fig.2 shows the visualization of the sparsity pattern of the normalized adjacency matrix and PPMI matrix of the Cora[19]dataset. From Fig.2, it can be seen that the PPMI matrix is denser than the adjacency matrix, i.e., the PPMI matrix embeds more latent relations between nodes.
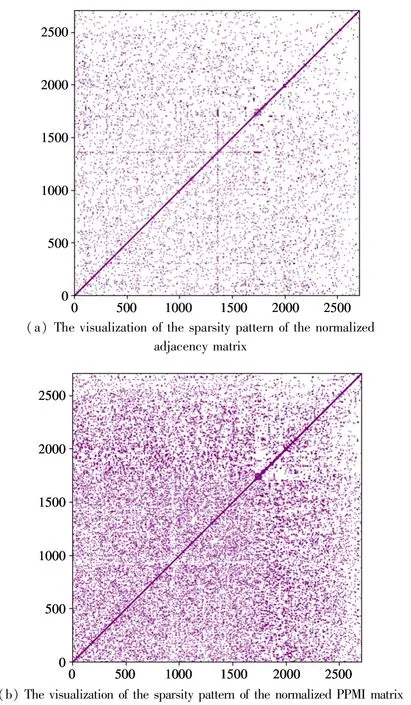
Fig.2 The visualizations of the sparsity pattern of the normalized adjacency matrix and PPMI matrix of the Cora dataset
3.2 Graph convolutional autoencoder
The graph autoencoder is usually composed of an encoder and a decoder. In the proposed method, the encoder consists of a 2-layer GCN[2]which fuses the PPMI matrix and the node contentXinto a latent and low-dimensional representation, and the decoder uses above latent representation to reconstruct the graph structureA.
3.2.1 Graph convolutional network
GCN[2]encodes the adjacency matrixAand node contentXinto the low-dimensional representation. Given a graphG= {V,E,X} with its adjacency matrixAand the spectral convolutional functionf(Z(l),A|

3.2.2 Graph convolutional autoencoder using PPMI matrix
In this work, a 2-layer GCN[2]is used as the encoder modelg(X,P). Instead of encoding node featureXand the adjacency matrixA,the proposed model embedsXand PPMI matrix into a low-dimensional space to better capture the semantic information of the graph data. The convolutional operation is defined asf(Z(l),P|W(l)):

3.3 Deep convolutional adversarial regularization
To improve the matching of the latent representationZand the prior distribution, the proposed model uses a deep convolutional adversarial training network,which is composed of a 2-layer GCN[2]and a fully connected layer. The adversarial modelD(Z) is formulated as

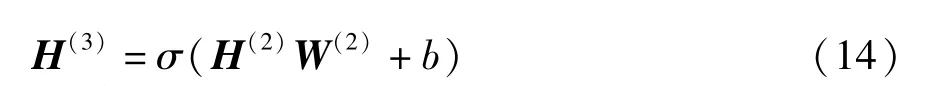
whereH(0)=Zis the input of the adversarial network,H(l)denotes the output oflth hidden layer of the deep convolutional adversarial network,H(3)represents the binary output of the adversarial network,σis the Sigmoid function, andbis the bias of the fully connected layer.
The adversarial model acts as a discriminator to distinguish whether the latent codeZcomes from the prior distributionp(Z) (p(Z) conforms to the Gaussian distribution) or from the graph encoder modelg(X,P). The loss function of the discriminator is a crossentropy loss related to the binary classifier, and the discriminator is optimized by minimizing the loss function.


Algorithm 2 DCAG-AE Input:graph G = {V, E, X} with adjacency matrix A;the number of epochs L;Output:the latent representation Z∈R N×D;the reconstructed graph structure ^A∈R N×N;1. Calculate the co-occurrence matrix C by Algorithm 1;2. Calculate PPMI matrix P by Eq.(4);3. for i=0 to L do 4. Encoder g(X, P)→Z according to Eq.(9);5. Sample m entities {a(1),…, a(m)} from the prior distribution p(Z);6. Sample m entities {z(1),…, z(m)} from the latent matrix Z;7. Calculate the output of the discriminator D(Z)by Eq.(14);8. Update the discriminator by∇1 m ∑m j=1[logD(a(j)) +log(1 -D(z(j)))]9. Decoder σ(ZZT)→^A according to Eq.(10);

10. Update encoder and decoder using Eq.(11);11. end for 12. return the latent representation Z and the reconstructed graph structure ^A.
Given a graphGand its adjacency matrixA, this work firstly calculates the nodes co-occurrence matrixCfollowing Algorithm 1 and then calculates the PPMI matrix according to the learnedC. Then, the encoder modelg(X,P) encodes the PPMI matrixPand node contentXinto the latent representationZ. After that,the same number of samples are sampled from the generated representationZand the real data distributionp(Z) to train the discriminator with the cross-entropy loss. Then the decoder reconstructs the graph structure^Abased on the latent representationZ. Finally, the encoder and decoder are updated by Eq.(11).
4 Experiments
To verify the effectiveness of the proposed model,three unsupervised analysis tasks are performed on the graph data: link prediction, node clustering, and graph visualization.
4.1 Dataset
This paper conducts experiments on 3 benchmark datasets. The details of these datasets are shown in Table 1. Cora, Citeseer and Pubmed[19]are all composed of citation networks, whose nodes represent the documents and edges represent the citation relations. All datasets are divided into training set, validation set and testing set. Among them, the validation set accounts for 5% to optimize the hyperparameters, the testing set accounts for 10% to verify the performance of the model, and the rest is used for training.

Table 1 The statistics of different datasets
4.2 Link prediction
This paper uses the reconstructed graph structure obtained from Eq.(10) to predict the edges and nonedges between the nodes in the testing set.
4.2.1 Baseline
Several classic link prediction methods are selected as the compared methods.
DeepWalk[4]is a graph embedding method,which encodes social relations into a continuous vector space by training Skipgram model[20]using short random walk strategy.
Spectral Clustering[21]learns the social embedding by generating a representation from the normalized graph Laplacian.
GAE[7]uses the graph convolutional network as its encoder and leverages both topological and content information to reconstruct the graph structure.
VGAE[7]is the variational version of GAE which learns the distribution of the latent representation.
ARGA[8]is an adversarially regularized autoencoder which uses the graph autoencoder to learn the low dimensional embedding of graph.
ARVGA[8]is the variational version of ARGA which also uses the graph autoencoder to learn the low dimensional embedding of graph.
4.2.2 Metrics
To measure the effectiveness of the proposed model on the link prediction task,the following two indexes are adopted: AUC score (the area under a receiver operating characteristic curve) and average precision(AP) score[7]. This work performs experiments 10 times for each dataset, and adopts the mean value with the standard errors as the final result.
4.2.3 Parameter settings
For Cora and Citesseer datasets, they have similar parameter settings because they have a similar number of nodes and edges. Therefore, the autoencoder model is trained for 220 iterations. The learning rate and discriminator’s learning rate are set as 0.005 and 0.001,respectively. Pubmed dataset has more nodes and edges, the model is trained for 350 iterations. The learning rate is set as 0.009 and discriminator’s learning rate is 0.001. For all experiments, the number of neurons of hidden layer and embedding layer are both set as 32, and the two hidden layers in the discriminator are set as 32-neural and 64-neural, the walk length of the random walk strategy is set as 2 and the total walk is set as 100. For the other baselines,the parameter settings are the same as that in the corresponding papers.
4.2.4 Results
The experimental results of link prediction task are shown in Table 2. For link prediction task, the proposed model outperforms all other baseline methods, achieving state-of-the-art results on the three benchmark datasets. All theAUCandAPscores are as higher as 97%. For the Cora dataset, the method improves theAUCscore by 5.6% compared with the ARGA or ARVGA and improves theAPscore by 4. 2%and 4. 8%, respectively, compared with the ARGA and ARVGA. For Citeseer dataset, the proposed method improves theAUCscore by 7.4% and theAPscore by 6.1% compared with the ARGA,18.8% and 15.5%compared with DeepWalk. On the Pubmed dataset,the method improves upon the ARGA by 1.9% in terms of theAUCscore and 1.5% in theAPscore. In addition,the standard errors of the proposed method are smaller,indicating that the model is more robust.
4.2.5 Parameter study
Change the walk length of the random walk strategy from 1 to 10 to learn the effect of walk length on embedding. The results of the Cora dataset are shown in Fig.3.

Fig.3 The embedded performance on different walk lengths of the Cora dataset
When the walk length is equal to 1, the PPMI matrix contains only the information of the node itself,which results in the learned embedding being invalid.When the walk length is 2,the embedding performance is the best. At this time, the PPMI matrix embeds the semantic information of the first-order and second-order neighbor nodes, which are also the neighbor nodes that has the greatest semantic correlation with the node. As the walk length increases, although the PPMI matrix captures the semantic information of higher-order neighbor nodes, it also embeds some semantic information with lower correlation. So, there must be a balance between more neighbor semantic information and neighbor information with higher semantic correlation.
4.3 Node clustering
After learning the latent embeddings, this paper uses the spectral clustering algorithm to cluster the nodes of the graph.4.3.1 Baseline
In addition to the baselines compared in the link prediction task, it is also compared with other state-ofthe-art clustering algorithms.
Kmeans is the basis of many clustering algorithms. Graph Encoder[22]uses a stacked autoencoder to learn representations for spectral graph clustering.DNGR[16]uses a stacked denoising autoencoder to reconstruct the PPMI matrix for learning a low dimensional embedding. RMSC[23]is a multi-view spectral clustering approach which considers both the information view of structure and content data. TADW[24]is based on matrix decomposition which adds node feature for the representation learning.
4.3.2 Metrics
In this paper, the following four indexes are used to measure the effectiveness of the proposed model on the node clustering task: accuracy (ACC), normalized mutual information (NMI), precision, F-score (F1)and average rand index (ARI).4.3.3 Results
The experimental results of node clustering tasks on the Cora and Citeseer datasets are shown in Table 3 and Table 4. Through the experimental results it can be seen that the proposed method performs better than other baselines for all evaluation metrics on the node clustering task. For instance, for the Cora dataset, the method outperforms ARGA by 7.1% in theACCscore,8.0% in theNMIscore and 16.5% in theAPIscore.For the Citeseer dataset,the proposed method improves theACCscore by 8.2% and theF1 score by 5.6%compared with the ARGA,the precision score by 6.8%and theNMIscore by 11.7% compared with the ARVGA.

Table 3 The results of node clustering on the Cora dataset

Table 4 The results of node clustering on the Citeseer dataset
4.4 Graph visualization
t-SNE algorithm[25]is used to realize the visualization of Cora dataset in the two-dimensional space.Fig.4 shows the visualization results using different walk lengths on the Cora dataset.
As the walk length increases, the nodes in the cluster are close to each other. To verify this view, the intra-cluster distance is calculated, which is defined as the average value of the Euclidean distance from the node to the centroid in the cluster. As the walk length increases, the intra-cluster distance gradually decreases, therefore, the embeddings of the nodes in the cluster are more similar to each other. When the walk length increases, the nodes will obtain richer context information, and the nodes with similar contexts will obtain similar low-dimensional representations.
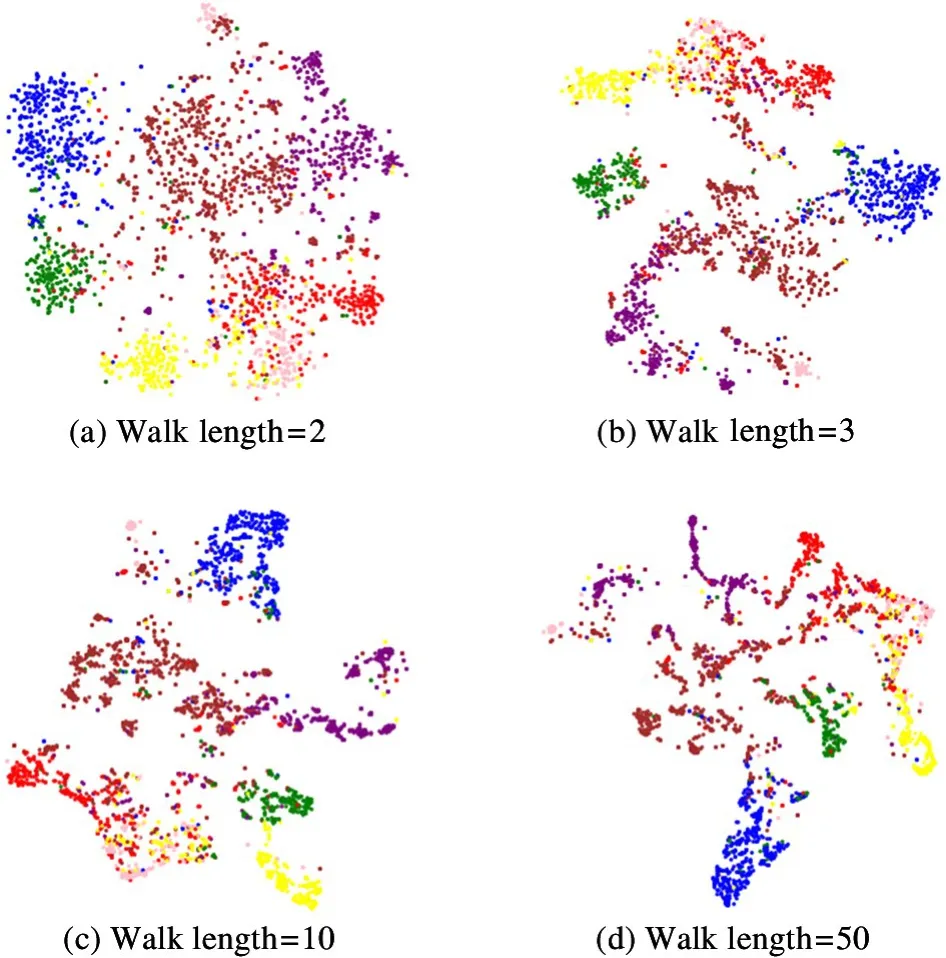
Fig.4 Visualization of the Cora dataset on embeddings generated by DCAG-AE using different walk lengths. From left to right, the intra-cluster distance = {1. 221, 0. 902,0.662,0.548}
5 Conclusions
A novel deep convolutional adversarial graph autoencoder using PPMI matrix for graph embedding is proposed. Most of the existing graph embedding algorithms only focus on the topological information of the graph data, and ignore the semantic information of the graph data. To capture the semantic information between nodes, the proposed model encodes the PPMI matrix generated by the random walk strategy and the node content information into a latent representation,and then uses this latent representation to reconstruct the graph structure. Additionally, to enhance the robustness of embedding, this paper introduces the deep convolutional adversarial training schemes. The effectiveness of the proposed model is verified by evaluating the performance of link prediction, node clustering and graph visualization tasks on the benchmark datasets.
 High Technology Letters2022年1期
High Technology Letters2022年1期
- High Technology Letters的其它文章
- A joint optimization scheme of resource allocation in downlink NOMA with statistical channel state information①
- Personalized movie recommendation method based on ensemble learning①
- An improved micro-expression recognition algorithm of 3D convolutional neural network①
- Resonance analysis of single DOF parameter-varying system of magnetic-liquid double suspension bearing①
- Computation offloading and resource allocation for UAV-assisted IoT based on blockchain and mobile edge computing①
- A load balance optimization framework for sharded-blockchain enabled Internet of Things①
