A load balance optimization framework for sharded-blockchain enabled Internet of Things①
YANG Zhaoxin (杨兆鑫), YANG Ruizhe, LI Meng②, YU Richard Fei, ZHANG Yanhua
(*Faculty of Information Technology, Beijing University of Technology, Beijing 100124, P.R.China)
(**School of Information Technology, Carleton University, Ottawa K1S 5B6, Canada)
Abstract Recently, sharded-blockchain has attracted more and more attention. Its inherited immutability, decentralization, and promoted scalability effectively address the trust issue of the data sharing in the Internet of Things (IoT). Nevertheless, the traditional random allocation between validator groups and transaction pools ignores the differences of shards, which reduces the overall system performance due to the unbalance between computing capacity and transaction load. To solve this problem, a load balance optimization framework for sharded-blockchain enabled IoT is proposed, where the allocation between the validator groups and transaction pools is implemented reasonably by deep reinforcement learning (DRL). Specifically, based on the theoretical analysis of the intra-shard consensus and the final system consensus, the optimization of system performance is formed as a Markov decision process (MDP), and the allocation of the transaction pools, the block size, and the block interval are jointly trained in the DRL agent. The simulation results show that the proposed scheme improves the scalability of the sharded blockchain system for IoT.
Key words: Internet of Things (IoT), blockchain, sharding, load balance, deep reinforcement learning (DRL)
0 Introduction
Recently, with the emergence of blockchain technology, the integration of blockchain and the Internet of Things (IoT) has received great attention in both industry and academia[1-4]. On one hand, IoT is entering a new phase of cross-industry integration, merging data generated from various systems or domains to construct a more powerful industrial sector, and thus requiring a dedicated and large-scale cross-industry platform[5].However, the current centralized architecture in the IoT network is challenged by single point of failure(SPOF), data privacy, reliability, and robustness[6].On the other hand, the blockchain emerges by combining cryptography, distributed consensus, and chained-block of data recording. With these advantages of decentralized management and immutable storage,blockchain has been regarded as one of the most reasonable candidates to address the above issues of IoT[7].
Blockchain firstly worked as a cryptography-based decentralized public ledger to store transactions for Bitcoin[8]. Then, along with Ethereum[9], the implementation of decentralized applications with smart contract was developed. It means that the blockchain technology can be used for the management of the interactions in generalized multi-peer systems (e.g., IoT systems). Subsequently, researches put more effort into applying blockchain to IoT networks. For example,Ref.[10] introduced a new IoT architecture to implement task offloading and resource allocation through smart contracts on blockchain. Ref.[11] focused on structural applications incorporating IoT and blockchain into distributed systems. However, with the expansion of blockchain application scenarios, transaction throughput, as an important indicator of system performance, has become the key point of improvement.
Fortunately, sharding comes up with the increase in throughput by parallelizing the verification process of the blockchain[6]. A representative platform is Zilliqa[12]that maximizes the blockchain throughput in proportion to the number of shards. Meanwhile, Ethereum 2. 0 proposed a version of a sharded blockchain that splits the entire network into multiple portions.
However, due to the impossible triangle of the blockchain that decentralization, security, and scalability cannot be satisfied at the same time, various approaches have been proposed to balance this three-way trade-off issue. Specifically, many studies have focused on performance optimization schemes using reinforcement learning. Ref.[13] proposed a DQN-based blockchain scheme for the IoT network, which optimizes the blockchain throughput under decentralization and security constraints. In Ref.[14], a shardedblockchain optimization framework based on DQN maximized the throughout by adjusting the shard number and other blockchain parameters while ensuring consensus security.
Nevertheless, the load unbalance issue exists in the blockchain system due to uneven distribution between the different computing resources of nodes and the different requirements of various blockchain users.On one hand, in order to address the heavy computation load of the mining clusters of the blockchain enabled cellular V2X networks, Ref.[15] proposed a game-theoretic approach for balancing the load at mining clusters while maintaining fairness among offloading vehicles. In addition, Ref.[16] proposed a blockchain-based storage system with financial incentives for load-balancing the data storage between nodes. On the other hand, for the requirement differences of users,for instance, a single user is involved in a great number of transactions, monoxide blockchain system[17]resolves the issue with the co-design of a virtualization applications at the upper layer, which virtualize the user addresses in different shards for load balancing.However, few studies have been published on the load balance between validator groups and transaction pools. There are often significant performance differences between nodes in the real blockchain system,and these differences directly result in an even distribution of nodes with different performance within each shard. Although the random sharding method reduces the risk of a shard being controlled by a malicious node, the large difference between shards usually affects the throughput of the blockchain and, therefore the quality of service for users.
In order to ensure the shards’ load balance and improve the system throughput, in this paper, a performance optimization framework for sharded-blockchain enabled IoT is proposed based on deep reinforcement learning (DRL), where the allocation of the validator groups and transaction pools is done according to the computation capacity and transaction load. The contributions of this paper are summarized as follows.To meet the needs of data sharing in large-scale IoT networks, a sharded based permissioned blockchain for IoT is proposed, where transactions are parallelly processed by validator groups. To keep the load balance of different shards, the transaction load requirements is quantified based on the computation cost of intra-shard consensus and its theoretical analysis of performance.Then, the shard forming (allocating the validator groups to transaction pools) and the parameters adjustment (block size and block interval) is formulated as a joint optimization problem and solved by using DRL.Simulation results are presented to show the effectiveness of the proposed scheme.
The rest of this paper is organized as follows. Section 1 describes the system model, followed by the theoretical analysis of consensus protocols in Section 2.Then,the problem formulation is presented in Section 3.Simulation results are shown and discussed in Section 4.Finally, in Section 5, the conclusions and future work are given.
1 System model
In this section, the structure of the sharded blockchain for IoT networks is introduced first, followed by its two-phase consensus.
1.1 Sharded-blockchain based IoT networks

Fig.1 Blockchain-based IoT network via sharding
The structure of the blockchain-based IoT network is illustrated in Fig.1, in which smart devices collect ambient data, which might be shared and processed among different applications (e.g., smart factory,smart home, smart grid, medical care, monitoring systems, etc.)[14]. For instance, the traffic monitoring data captured by road side units (RSU) and the location information of smart vehicles might be required for route navigation and traffic condition prediction. Here,the sharing of data is recorded in transactions running on a scalable blockchain via sharding, so that secure data storage and reliable data management are implemented.
To meet the needs of a large-scale IoT system,sharding on the blockchain is required to process massive transactions in a parallel manner, where consensus nodes (validators) are clustered into different validator groups to deal with different transactions at the same time[18]. Specifically, validators of sizeNare divided into a directory committee (DC) containingCnodes andKvalidator groups in a random manner, and accordingly, transactions are allocated toKvalidator groups. In each shard, the local blocks composed of local transactions are produced via intra-shard consensus. Then all of these local blocks need to be validated via the final consensus in the DC. Finally, the verified local blocks with no faults will be merged to final blocks and will be distributed to all the blockchain nodes. Note that all of the consensus adopt the practical Byzantine fault tolerance (PBFT) protocol,and the nodes take turns being distributed into different shards,producing a block of sizeSB(in bits) in an interval ofTI(in seconds).
1.2 Two-phases PBFT consensus model
The PBFT is a revolutionary protocol to meet the Byzantine general’s problems[19]. It can significantly reduce the message complexity of reaching consensus from the exponential level to the polynomial level and still tolerate the proportion of malicious peers (1/3).The classic PBFT protocol mainly consists of three steps: pre-prepare, prepare and commit. Based on the classic PBFT protocol, a two-phase consensus model adapting to sharded-blockchain is shown in Fig.2[12].It contains intra-shard consensus and final shard consensus.
The intra-shard consensus using the PBFT protocol within a shard is presented as follows.
(1) The selected primary node in each shard is responsible for collecting the transactions and generating new local blocks as well as broadcasting blocks to the local shard via pre-prepare messages.
(2) Each replica node receives the block and verifies the set of transactions in the block, then exchanges the hash digest with other replica nodes.
(3) The nodes who would receive the most (2/3)same hash digests broadcast its commit message.
(4) All the validators, including the primary node, exchange the commit messages between each other, if the primary node receives the most (2/3)commit messages.

Fig.2 Two-step consensus structure of shard based blockchain
After the local commit phase, the primary and the replica nodes reply their intra-shard consensus to the DC for the final consensus.
The final consensus in DC also runs the PBFT protocol.
(1) The selected primary node selected in DC network is responsible for collecting the blocks from the shardings, and generating and broadcasting the final blocks.
(2) Each DC replica node receives and verifies the set of transactions in the final blocks, then exchanges the hash digest with other DC replica nodes.
(3) The node who would receive the most (2/3)same hash digests broadcasts a commit message.
(4) All the validators exchange the commit message between each other, if the primary node receives the most (2/3) commit messages.
After the commit phase in DC, the DC nodes reply the final consensus to all the clients in IoT network. Transactions over the two-phase consensus are stored into the blockchain immutably.
2 System performance analysis
In this section, the consideration of the load balance of sharding is presented, and the corresponding theoretical analysis is given. For the clarity of following discussion, the notations are summarized in Table 1.
2.1 Overview of the load balance protocol
As described in Section 1.1, shards are formed by grouping the validators to different transaction pools. The nodes within one shard produce and verify the local blocks, which contain the block number,block size, signed block summary and transactions.After the intra-consensus, the local block is submitted to the directory committee, where the block header is added if it passes the final consensus.

Table 1 Notations
It is worth noting that transactions randomly generated in real time may lead to uneven throughput demands in different shards. Meanwhile, the computation capacity of validator groups is different due to the random grouping of consensus nodes. Therefore, the work load of different shards will be unbalanced if a shard is congested with a large number of transactions. Specifically, if a shard with a heavy work load has poor processing capacity (the local primary or replicas have poor computation capacity), the intra-consensus will be delayed and the throughput of the entire blockchain system will be affected. Therefore, the allocation between the validator groups and the IoT transaction pools should be reasonable to ensure the load balance among the shards.
2.2 Load balanced performance theoretical analysis
2.2.1 Intra-shard consensus validation time
Here, the detailed steps and theoretical analysis of the load balance between the shards and the transaction pool is given.


(1) Request: the IoT devices send requests for block validation to the primary, then the primary verifies one MAC for each transaction request, each request contains one signature that requires verification for each replica during the consensus process.
(2) Pre-Prepare: the primary node processes the requests (xkrequests operated from thek-th transactions pool in time slot) in a single pre-prepared message and forwards the message to all replica nodes. In this phase, the primary node generates(Nk-1) MACs to send the pre-prepared message, and each replica node needs to verify one MAC.
(3) Prepare: each replica node authenticates the pre-prepare message and generates (Nk- 1) MACs to all the other replicas, and verifies (Nk- 2) MACs when they receive them. Meanwhile, the primary node needs to verify (Nk- 1) MACs received from all the replicas.
(4) Commit:all the validators,including the primary node, exchange the messages between each other, so the primary and any replica first send and then receive(Nk-1) commit messages, which need to generate(Nk-1) MACs and verify(Nk- 1) MACs, respectively.
At the end of the commit phase, the primary and all the replica nodes reply their intra-shard consensus to the DC for the final consensus. At this time,the primary and replica nodes createCMACs for each request.
Note that the primary node performs totalxksignature checks andxk(C+ 1)+ 4(Nk- 1) MAC operations, and replica nodes perform a totalxksignature checks andxkC+ 4(Nk- 1) operations. The computing load of primary nodes and replica nodes arexkCα+ [xk(C+ 1)+ 4(Nk- 1)]βandxkCα+ [xkC+4(Nk-1)]β,respectively.
Thus, the validation time of primary node and replica nodes can be expressed as follows.


2.2.2 Load balanced shard allocation
Based on Eqs(3) and (4), the intra-shard validation time will not be delayed if a transaction pool with a higher transaction load is allocated to a validator group with higher computation capability. In order to avoid the load imbalance, the allocation between validator groups and transaction pools should minimize the system’s longest intra-shard validation timeT˙val.
The allocation forKvalidator groups andKtransaction pools can be represented as

andδi(t)=j(i,j∈{1,2,…,K}) means that thei-th transaction pool is allocated toj-th validators group at time slott.
Since the nodes in the IoT usually have limited computation resources[20],here,the computation capability ofk-th validator groups is modelled as a random variableμk=ck,minwith the node with the least computation capability. Due to various tasks in the IoT system, it’s hard to know the computation capability of each node at the next time instant. Assuming the value of computation capability can be partitioned intoHdiscrete intervals, denoted asΨ= {Ψ0,Ψ1,…,ΨH-1},the computation capability of shardkat time slottcan be expressed asμk(t).
Considering the time correlation of computation states in nodes, the transition of computation capability is modelled as a Markov chain. Thus,theH×Htransition probability matrix is defined as [pμ]H×H, where[pμ]h,h′= Pr[μk(t+ 1)=Ψh|μk(t)=Ψh′] andΨh,Ψh′∈Ψ.Here, the set of computation capability ofKvalidator groups is donated by U(t)= {μ1(t),μ2(t),…,μk(t),…,μK(t)}.
Similarly, the transactions generated ink-th transaction pool is also modelled as a random variableχk.Assuming the value of transaction load can be partitioned intoLdiscrete intervals, denoted asX= {X0,X1,…,XL-1},the transaction load of transaction poolkat time slottcan be expressed asχk(t).
Considering the time correlation of the IoT transactions pool, the transition of the number of generated transactions within thek-th transaction pool is modelled as a Markov chain. Thus, theL×Ltransition probability matrix is defined as [pχ]L×L, where [pχ]l,l′=Pr[χk(t+1)=Xl|χk(t)=Xl′] andXl,Xl′∈Χ.Here, the set of transaction load ofKtransaction pools is donated byX(t)= {χ1(t),χ2(t),…,χk(t),…,χK(t)}.Algorithm 1 shows the detail of load balance allocation scheme for sharded-blockchain-enabled IoT.

Algorithm 1 Load balance allocation scheme for shardedblockchain-enabled Internet of Things Initialization:Randomly partition of the IoT network into K transaction pools Randomly grouping of the consensus nodes into K validator groups Input the transaction load set of K transaction pools {χ1(t),χ2(t),…,χK(t)}Input the computation capability set of K validator groups{μ1(t), μ2(t),…, μK(t)}Input the number of consensus nodes N Initialize the shard allocation:ΔK(t) = {δ1(t),δ1(t),…,δi(t),…,δK(t)}

for t = 1,2,…,O do for δi(t) = j do Allocate the i-th transaction pool to j-th validator group Load balanced allocation by minimizing the system’s longest intra-shard validation time T˙val End for Adjust the block sizes and block intervals by maximizing the throughput Θ(SB, TI)DQN optimization of the allocation and the parameters adjustment Apply the training result to the sharded-blockchain enabled IoT system End for
2.2.3 Scalability performance
The scalability of a sharded-blockchain system can be evaluated by system throughput, which is the number of transactions packed into local blocks in a unit time. Usually, the throughput of the traditional blockchain is affected by two performance parameters: block size and block interval. Noting that the sharded-blockchain produces blocks in a parallel manner, the throughput isKtimes increased, which can be expressed as[14]

whereSBrepresents the local block with a maximum size (bytes) for each block interval periodTI,SBHandλare the block header of the local block and the average transaction size respectively. Considering the fixed shard number, it can be found from Eq.(6) that increasing the block size or reducing the block interval can increase the throughput.
3 Problem formulation
In order to keep the load balance and improve the throughput of the sharded blockchain,it’s necessary to jointly optimize shard allocation, block size, and block interval. To implement the DRL approach, the system performance optimization problem is formulated as Markov decision process (MDP).

Fig.3 MDP of load balanced sharded blockchain
3.1 MDP formulation
3.1.1 State space
Due to the fact that the learning agent makes decisions about the allocation between the validator groups and the transaction pools, the system stateS(t) at time instantt(t= 1,2,3…) can be expressed as

where U(t) represents the set of computation capability ofKshards andX(t) is the set of transaction load ofKtransaction pools.
3.1.2 Action space
In order to optimize the shard allocation and maximize the throughput, several parameters of the blockchain system should be adjusted to adapt to the dynamic environment, which includes the shard allocationΔ(t), block sizeSBand block intervalTI.Thus, the action space at decision epochtis expressed by

3.1.3 Reward function
The reward function is defined to maximize the blockchain throughput while minimizing the longest system intra-shard validation time, and a decision should be made in each epoch to solve the following problem.

where theωL,ωT∈(0,1] are the weights coefficient for the trade-off between throughput rewards and the load balance rewards in order to get a reasonable training result. And there isωL+ωT= 1.
3.2 DQN-based optimization
Based on the formulation in Section 3.1, a DRL approach is used to optimize the reward. Specifically,a DNN-basedQ-learning approach is applied to perform complicated function approximation, which is known as DQN technology[21].
DQN is an improved version ofQ-learning that uses deep networks to approximate the action-value functionQ(S,A) instead of using aQ-table to storeQ(S,A),which is able to approximate the value function accurately while addressing a large volume data dimension. Algorithm 2 shows the optimization framework of system performance based on DQN.

Algorithm 2 DQN-based optimization framework for loadbalanced sharded blockchain Initialization:Initialize the system state of the sharded blockchain S(t)Initialize replay memory D with the capacity Z Initialize main Q network of Q(S,A;θ) with random weights θ Initialize target Q network of Q—(S, A; θ—) with weights θ=θ—Load initial state space S(t) data and use it as the input of the main deep Q network Input maximum training episode M,maximum training step T·DQN learning process:For episode=1,…,M do for t=1,…,T·do Select a random probability p if p <ε then do Select a random action else A(t) = arg max A Q(S,A;θ)

end if Decrease exploration probability ε Execute action A(t) to select allocation and adjust block size and block interval, and observe reward R(t) and proceed to next state S(t+1)Store the experience(S(t), A(t), R(t), S(t +1)) into the replay memory D Randomly sample a mini-batch of state transition (S(i),A(i), R(i), S(i +1)) from the replay memory D Set yi = ri +γ maxA′Q(Si+1, A′;θ—) to compute the target Q— value from the target Q network Update target Q network by performing the gradient descent of loss function L(θ) = (yi - Q(Si,Ai;θ))2 for every G step End for End for
4 Simulation results and discussions
In this section, the computer simulation is used to demonstrate the effectiveness of the proposed scheme.The simulation settings are presented. The related parameter settings are illustrated in Table 2.
4.1 Simulation setting
The computation capability of the validator is formulated as a Markov model. Assuming that the state of the computation capability can be very high,high,medium, and low, whose transition probability matrix[pμ]H×His set as


Table 2 Parameters of the system simulation environment
Similarly, assuming the state of transaction load of transaction pool can be very high, high, medium, and low, the transition probability matrix[pχ]L×Lis set by

For comparison, three baseline schemes are considered in the simulation as follows.
(1) Proposed scheme without load balanced allocation: theKtransaction pools are allocated toKshards in a random manner.
(2) Proposed scheme with fixed block size: the blocks generated by the block producers at different intervals with the same size (2 MB).
(3) Proposed scheme with fixed block interval:the frequency of issuing blocks is fixed (every 10 s).
4.2 Simulation results and discussion
4.2.1 Convergence trend analysis
Fig.4 shows the convergence performance of the long term reward under the proposed DQN-based load balanced sharded blockchain optimization scheme,where they-axis denotes the long term reward and thex-axis denotes the training episodes. From Fig.4 it can be observed that the convergence trend of the long term reward with the learning rate of 0.01 is not obvious.With the learning rate decreasing to 0.001, the convergence speed of the network is accelerated. The result is ideal when the learning rate is reduced to 0.0001, where the convergence is evident and the long term reward is higher than the others.

Fig.4 Long term reward under different learning rates
In addition, it can observed that the long term reward is lower at the beginning of the learning process.However, with the increase of episodes, the long term reward increases and reaches a stable state after around 2000 episodes, which means that the agent has learned the optimal strategy to maximize long-term reward. The convergence verifies the effectiveness of the proposed scheme.
4.2.2 Load balance performance analysis
Fig.5 describes the load balance performance with the proposed DRL-based performance optimization scheme. The longest intra-shard validation time of the proposed scheme decreases and reaches stable after 2000 episodes, which means the shard allocation became reasonable. Compared with the traditional random scheme, the proposed scheme can be verified to receive a more reasonable allocation according to the simulation result.
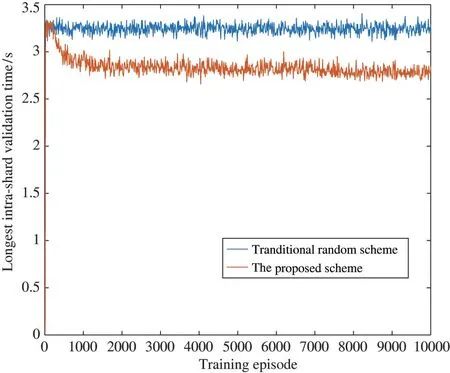
Fig.5 Comparison of longest intra-shard validation time
Fig.6 shows the relationship between system performance and the number of validators. One observation is that the validation time increases with the validators number increasing. With more validators joining the consensus process, the computing load of each transaction increases, which naturally leads to a decrease in system performance. In addition, focusing on the comparison with the traditional scheme, the proposed scheme obtains less validation time with the variation of validator number. The reasons are described as before.
Fig.7 shows the longest intra-shard validation time of the proposed scheme under different shard numberK. It can be found that latency of intra-shard consensus decreases with the increase of shard number. The reason is that with the increasing number of shards,the consensus nodes within a shard decreases, which reduces the computation cost for the intra-shard consensus validation. In addition,the transaction load of each transaction pools decreases with the increase of shard number. Therefore, the load balanced shard allocation can be got faster with more shard number.

Fig.6 Longest intra-shard validation time vs the number of validators

Fig.7 Longest intra-shard validation time under different shard numbers
4.2.3 Throughput performance analysis
Fig.8 shows the throughput performance of the proposed scheme under different baselines. It can be observed that the throughput is lower at the beginning of the learning process. However, with the increasing number of episodes, the throughput increases and reaches a stable state after around 2000 episodes, which verifies the convergence performance of the proposed scheme. In addition, it can be also found that the proposed scheme can receive higher throughput than that of the other baselines, which shows the advantage of the proposed framework.
Fig.9 shows the throughput performance of the proposed scheme under different shard numberK. It is obvious that the convergence of throughput slows down as the number of shards increases. The reason is that with the increasing number of shards, the action space of MDP becomes larger. For instance, when the shard number is 4, which means that 4 transaction pools should be allocated to 4 validator groups, thus it has totally 24(4 ×3 ×2 ×1) allocation methods. Then,the action space for the shard allocation is 24. When the shard number is 5,the action space of the shard allocation becomes 120. Therefore, the DQN agent needs more training episode to explore a more reasonable action.

Fig.8 Throughput performance under different baseline

Fig.9 Throughput performance under different shard numbers
Fig.10 shows the relationship between system performance and the average transaction size. It can be observed that with the average transaction size increasing, the throughput of the system decreases. The reason is that the number of transactions contained in one block decreases when the average transaction size increases. Focusing on the comparison of different schemes,the proposed scheme maintains the highest throughput with the different average transaction size, followed by the proposed scheme with fixed interval and block size.The reason is that the proposed scheme without any limiting factors is able to adjust a reasonable blockchain parameters to improve throughput.
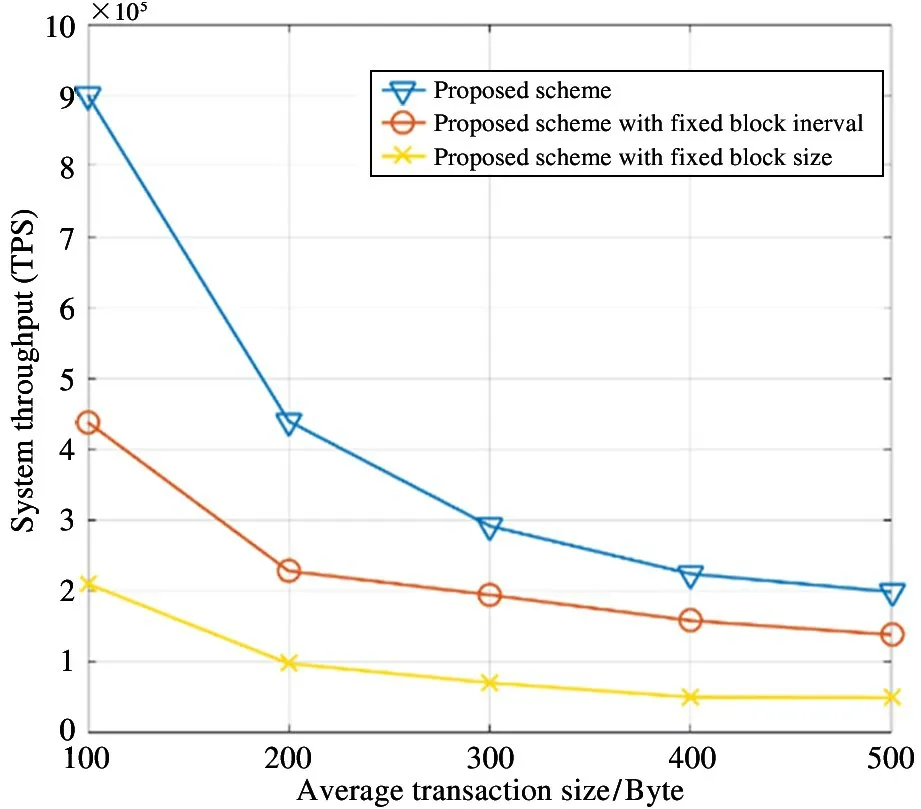
Fig.10 Throughput vs. transaction size
5 Conclusions
In this paper, a DRL-based load-balanced sharded-blockchain for the IoT network is proposed, where the allocation between the validator clusters and the transaction pools is load balanced and the scalability is improved. With sharded blockchain, the large scale data sharing of the IoT network is stored immutably and managed reliably. In the proposed framework, a theoretical analysis of the performance of sharded blockchain system is provided first. Then the load balanced allocation is optimized by the constraint of the shard’s longest validation time and by maximizing the load balanced parameter using the DQN approach. In addition,the throughput is maximized by adjusting the block size and block interval with DQN. Simulation results demonstrate the proposed framework can achieve reasonable load balanced allocation and higher throughput than the baselines with various system parameters. Future work is in progress to consider the optimization of shard number with other DRL approaches based on the proposed framework.
 High Technology Letters2022年1期
High Technology Letters2022年1期
- High Technology Letters的其它文章
- Deep convolutional adversarial graph autoencoder using positive pointwise mutual information for graph embedding①
- A joint optimization scheme of resource allocation in downlink NOMA with statistical channel state information①
- Personalized movie recommendation method based on ensemble learning①
- An improved micro-expression recognition algorithm of 3D convolutional neural network①
- Resonance analysis of single DOF parameter-varying system of magnetic-liquid double suspension bearing①
- Computation offloading and resource allocation for UAV-assisted IoT based on blockchain and mobile edge computing①
