基于分数阶滑模自适应神经网络的中速磁浮列车运行控制方法
张文静,曹博文,刘曰锋,岳 强,徐洪泽
(1. 北京交通大学电子信息工程学院,北京 100044;2. 中国铁道科学研究院集团有限公司机车车辆研究所,北京 100081;3. 中车唐山机车车辆有限公司产品研发中心,河北唐山 064000)
磁浮列车利用电磁力实现自身的悬浮、导向以及牵引驱动。与传统的轮轨交通方式相比,磁浮交通具有噪声低、线路适应性强、牵引制动性能好、维护工作量小以及寿命长等优点[1]。随着长沙磁浮快线和北京S1线等中速磁浮线路相继开通运营,广东清远磁浮旅游专线、湖南凤凰磁浮项目等相继投入建设,成都、阜阳等地相继规划建设中速磁浮试验线,中速磁浮列车(速度≤200 km·h-1)有望成为我国21世纪的新型轨道交通方式之一。
中速磁浮列车的运行控制系统(Operation Con⁃trol System,OCS)是用于列车运行指挥与安全防护的关键技术装备,运行控制算法是其核心技术之一。既有的中速磁浮列车OCS 主要借鉴传统轮轨列车的基于通信的列车自动控制系统(Communi⁃cation-Based Train Control System,CBTC)。针对传统轮轨列车运行控制算法,国内外学者进行了深入研究,如文献[2]设计自适应模糊滑模控制算法,补偿列车运行过程中的各项扰动,有效提高了列车停车制动精度;文献[3]通过分段线性化列车运行阻力,建立了动车组混合整数列车运行模型,并利用模型预测控制算法实现列车运行控制,保障了列车安全高效运行;文献[4]利用一种双自适应广义预测控制算法实现列车运行控制,提高了运行中列车速度与位置的跟踪精度以及输出结果的抗干扰能力。然而,与传统轮轨列车的牵引方式不同,中速磁浮列车的牵引控制系统位于地面,借鉴CBTC 系统设计的列车运行控制算法没有考虑磁浮交通的自身特性,难以完全适用。因此,有必要分析运行阻力对中速磁浮列车的影响,设计新的运行控制算法,从而提高列车运行性能。
目前,对中速磁浮列车的研究主要集中在悬浮控制方面[5-7],运行控制算法方面的研究相对较少。在中速磁浮列车运行过程中,运行阻力对列车位置与速度跟踪精度的影响较大,这就要求列车运行控制算法能够准确补偿运行阻力。从算法角度来看,分数阶(Fractional Order,FO)控制算法相比传统的整数阶控制算法具有更好的精度与鲁棒性[8],正随着分数阶微积分以及分数阶自适应控制理论的发展[9-10]而逐渐成为改善控制系统性能、提高控制精度的重要方法之一[11-12];滑模自适应控制(Sliding Mode Adaptive Control,SMAC)算法具有非线性控制精度高、鲁棒性强等优点[13],已在磁力机械[14]和车辆线控转向系统[15]等领域得到广泛的应用;神经网络(Neural Network,NN)算法能够有效估计并补偿永磁同步电机伺服系统和未知离散时间非线性动态系统中的非线性干扰项[16-17],切实提高控制系统的控制精度。因此,本文拟将上述3种算法相结合,估计并补偿中速磁浮列车的运行阻力,以满足对列车控制精度和鲁棒性的要求。
本文以中速磁浮列车为研究对象,首先在考虑列车实际运行过程中产生的运行阻力(空气阻力、涡流阻力以及坡道附加阻力)的基础上建立列车动力学方程;再设计基于分数阶滑模自适应神经网络(Fractional Order-Sliding Mode Adaptive Control-Neural Network,FO-SMAC-NN)的运行控制器,该控制器主要包括速度前馈、分数阶滑模自适应等效控制和自适应神经网络阻力补偿这3个部分;然后运用李雅普诺夫(Lyapunov)定理,证明基于该运行控制器的闭环控制系统稳定性;最后依托某中速磁浮列车仿真试验线及6 节编组的仿真列车,在理想情况和功率谱密度为108的白噪声干扰情况下,对比FO-SMAC-NN 运行控制器和PID 运行控制器控制下的列车运行性能,验证所提出运行控制器的有效性。
1 分数阶微积分定义及性质
黎曼-刘维尔(Riemann-Liouville,RL)分数阶微积分被广泛应用于各类工程实践中,其定义和基本性质如下。
1)RL分数阶积分
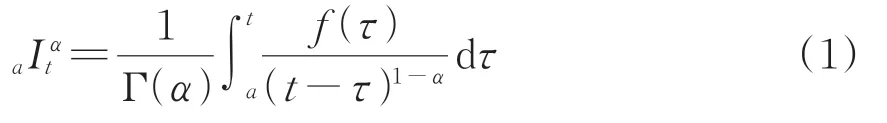
式中:α为积分阶次,且α∈R+;aI α t为分数阶积分算子,a与t分别为分数阶微积分上下限;Γ(·)为欧拉伽马函数。
2)RL分数阶微分
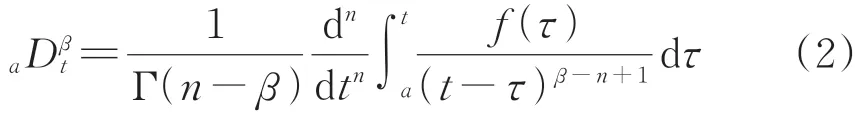
式中:β为微分阶次,且β∈R+;aDβt为分数阶微分算子;n∈Z+且n-1 <β<n。
3)RL分数阶微积分性质
性质1:若α=1,则在微分区间[a,t]内满足

性质2:若α,β∈R+,则在微分区间[a,t]内满足
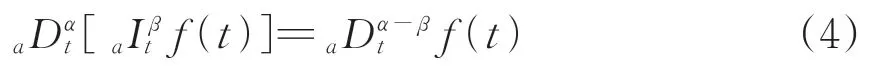
2 中速磁浮列车动力学方程
根据牛顿运动定律,建立中速磁浮列车的动力学方程

其中,
Fr=Fa+Fe+Fi
式中:m为列车质量;a为列车加速度;Ft为列车运行过程中受到的牵引力或制动力;Fr为列车运行阻力;Fa,Fe与Fi分别为列车受到的空气阻力、涡流阻力以及坡道附加阻力。
令控制输出u(t)=Ft,由式(5)得到中速磁浮列车的运动学方程为
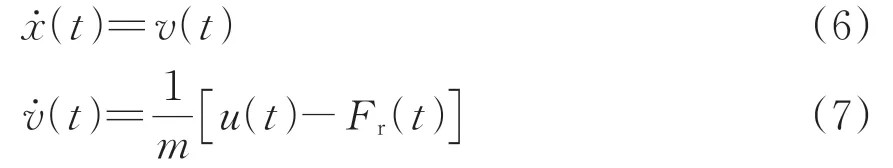
式中:x(t)为列车在t时刻的位移;v(t)为列车在t时刻的速度。
3 FO-SMAC-NN运行控制器设计
为了抑制运行阻力对列车位置与速度控制的影响,提高中速磁浮列车运行控制性能,将分数阶控制、滑模自适应控制、神经网络这3 种算法相结合,设计基于分数阶滑模自适应神经网络的运行控制器,在保证控制器稳定的情况下,利用神经网络估计列车运行阻力,利用分数阶自适应滑模面确保自适应算法具有更大的调节区间。最后运用李雅普诺夫稳定性定理,证明基于该运行控制器的闭环控制系统稳定性。
3.1 FO-SMAC-NN运行控制器结构
1)分数阶滑模自适应神经网络控制律
假设中速磁浮列车运行时的期望位移xd,期望速度vd以及期望加速度均有界,定义列车运行误差ex为

设计分数阶自适应滑模面为
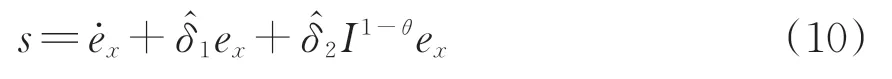
式中:和为待设计的自适应滑模参数;1-θ为积分阶次且θ∈(0,1)。
考虑到神经网络对未知非线性函数的拟合能力,本文利用径向基核函数(Radial Basis Func⁃tion,RBF)神经网络估计并补偿列车运行阻力,此时可将Fr改写为
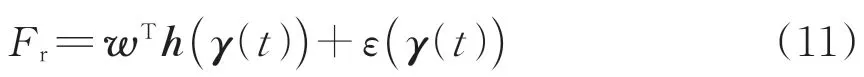
其中,
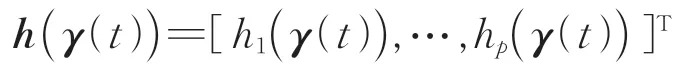
式中:p为神经元数量;w为神经网络的权重向量,w∈Rp;γ(t)为神经网络的输入向量,γ(t)=为神经网络误差,且ε(γ(t) )有上界,满足|ε(γ(t) )|≤ε0;h(γ(t) )为神经网络的基函数,h(γ(t) )∈Rp。
神经网络中第k个神经元的基函数h(γ(t) )可用高斯函数表示为
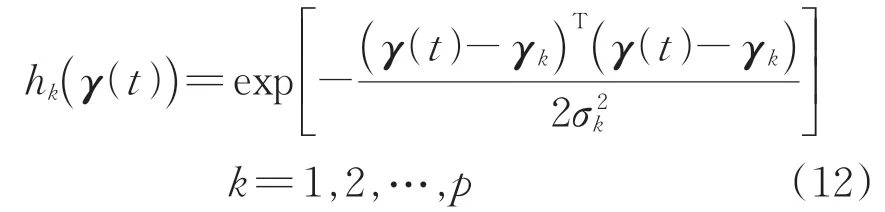
式中:γk和σk分别为神经元k的中心和宽度。
利用RBF 神经网络,定义中速磁浮列车运行阻力的估计值为

式中:为权重向量w的估计值。
根据式(12)和式(13),可将FO-SMACNN 运行控制器中神经网络参数w和ε0的估计误差分别表示为

式中:为神经网络误差ε(γ(t)) 的上界ε0的估计值。
为降低运行阻力对列车运行性能的影响,在式(6) 和式(7)的基础上,结合式(10)以及式(11)和式(13),基于李雅普诺夫定理,设计分数阶滑模自适应神经网络控制律为
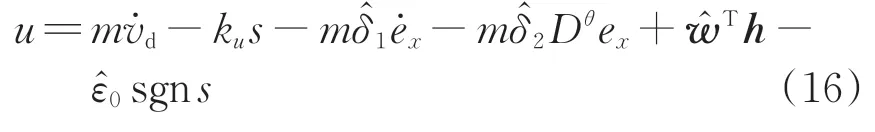
式中:ku为待设计的正参数;sgns为s的符号函数。
利用自适应更新律,实时更新式(16)中的各种参数。其中,滑模自适应参数和的更新律分别为

神经网络参数估计值和的更新律分别为

式中:Λ为待设计的正定矩阵;kε为待设计的正参数。
2)运行控制器结构
该FO-SMAC-NN 运行控制器的结构框图如图1所示。由图1可知,该控制器包含3 个部分:为速度前馈部分,可以改善控制系统的瞬态响应;为分数阶滑模自适应等效控制部分,可以提高对中速磁浮列车的运行控制精度及其鲁棒性;为自适应神经网络阻力补偿部分,可以实时估计并补偿列车运行阻力,改善运行控制效果。
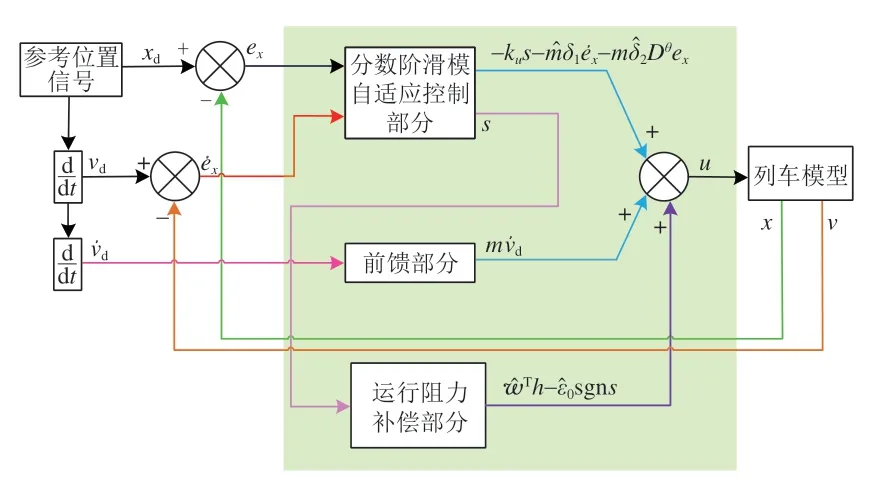
图1 FO-SMAC-NN运行控制器结构框图
3.2 控制系统稳定性证明
为证明系统稳定性,构造如下李雅普诺夫函数
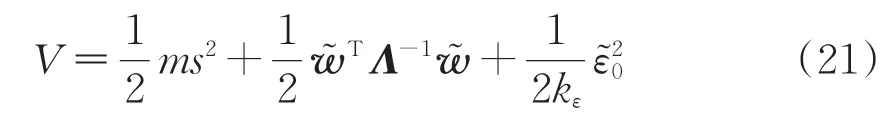
计算李雅普诺夫函数V的导数为
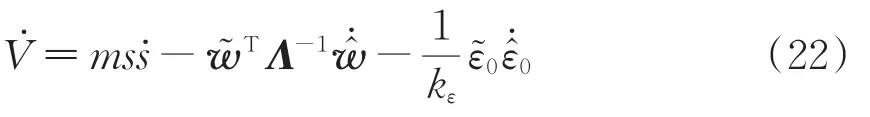
根据RL 分数阶微积分性质1 和2,由式(6)、式(7)和式(10)可得滑模面的变化率为
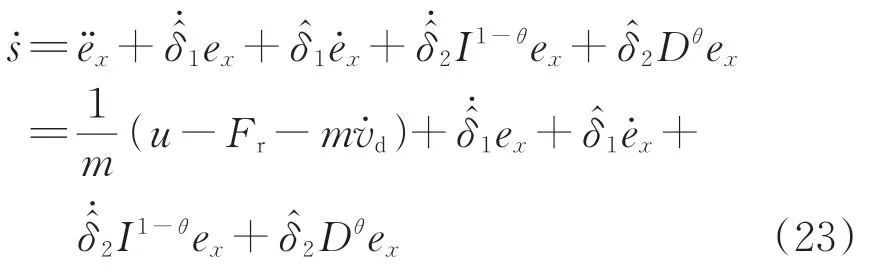
将式(16)和式(23)代入式(22),李雅普诺夫函数V的导数变换为
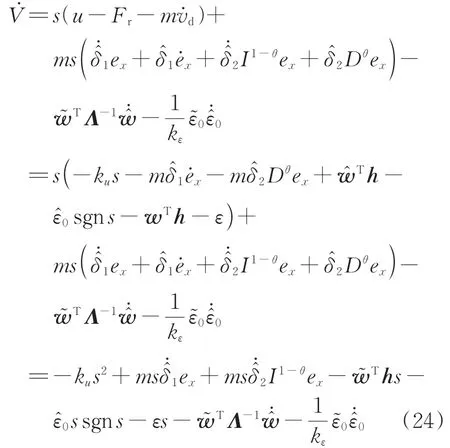
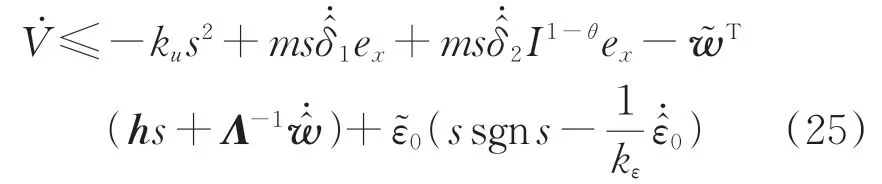
将式(17) 和式(18)以及式(19) 和式(20)代入式(25),得到
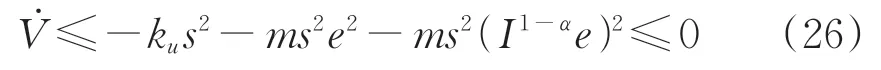
根据李雅普诺夫稳定性定理,s,和有界,当t→∞时,误差ex及其导数收敛至0,系统渐进稳定,这表明本文所设计的分数阶滑模自适应神经网络控制器可以保障中速磁浮列车稳定运行。
4 仿真验证
为了验证所提出FO-SMAC-NN 运行控制器的性能,基于某中速磁浮列车仿真试验线及仿真列车,分别在理想情况和噪声干扰情况下,仿真对比FO-SMAC-NN 运行控制器和目前已得到广泛应用的比例-积分-微分(PID)运行控制器控制下的列车运行性能。
4.1 仿真参数
某中速磁浮列车仿真试验线长10 km,相关各参数如图2所示。图中:R为曲线半径,m;i为坡道坡度的千分数,‰;绿色表示试验线限速,km·h-1;红色表示线路平面;蓝色表示试验线标高与坡度;黑色表示试验线公里标。用到的某6 节编组仿真列车,基本参数见表1。仿真过程中,列车运行时受到的3 种阻力根据式(27)—式(29)设置。
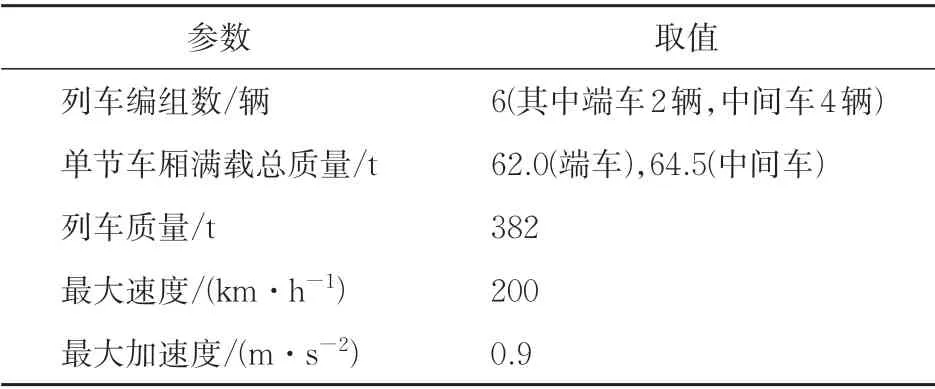
表1 仿真列车基本参数
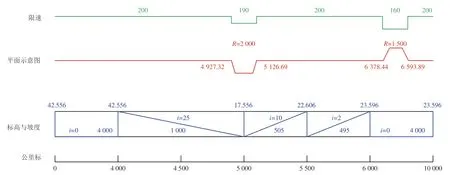
图2 中速磁浮列车试验线线路纵断面图
1)空气阻力
空气阻力Fa与列车车型、线路条件、空气阻力系数以及列车速度相关,计算式为

式中:N为列车的编组车辆数。
2)涡流阻力
涡流阻力Fe由磁浮线路两侧的F 轨与悬浮电磁铁间的涡流效应产生,应满足
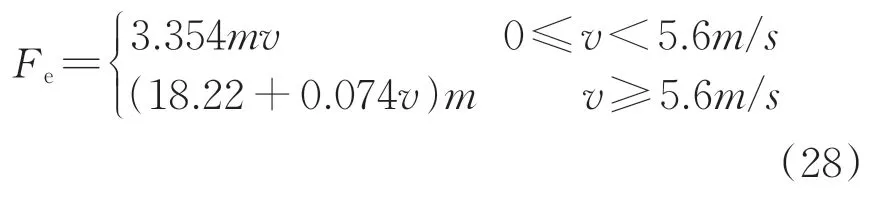
3)坡道附加阻力
中速磁浮列车经过坡道线路时产生坡道附加阻力Fi,其大小由列车质量以及坡道坡度决定,可以描述为

其中,
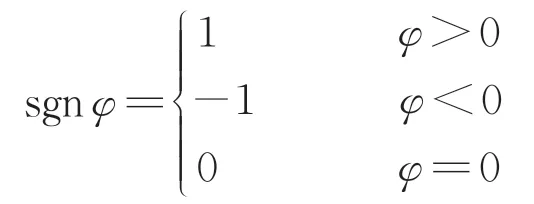
式中:g为重力加速度;φ为坡道角;sgnφ为φ的符号函数,取1 表示列车处于上坡状态,取-1 表示列车处于下坡状态,取0 表示列车处于平道状态。
4.2 控制器参数整定
FO-SMAC-NN 运行控制器和PID 运行控制器的参数整定过程如下。
步骤1:FO-SMAC-NN 等效控制参数与PID参数整定。忽略列车运行阻力,利用试凑法调节FO-SMAC-NN的等效控制参数ku;综合考虑系统的快速性与平稳性,利用MATLABTM工具箱整定PID 运行控制器的比例增益kP、积分增益kI和微分增益kD。整定后,FO-SMAC-NN 等效控制参数和PID运行控制器参数以及取值分别见表2。

表2 运行控制器参数及整定后取值
步骤2:分数阶参数整定。分数阶参数θ∈R+=且θ∈(0,1)。为了有效提高列车运行的控制精度与鲁棒性,忽略列车运行阻力,利用试凑法调节分数阶参数,使FO-SMAC-NN 运行控制器达到最佳控制效果,整定后的分数阶参数取值为θ=0.47。
步骤3:自适应参数整定。通常情况下,自适应参数值越大,收敛速度越快,然而过大的自适应参数会产生过拟合现象,影响列车运行阻力估计的准确性,造成系统震荡甚至导致系统不稳定。根据上述情况,在步骤1 和步骤2 的基础上,考虑列车运行阻力因素,利用试凑法整定自适应参数,使FO-SMAC-NN 运行控制器达到最佳控制效果。整定后的自适应参数取值分别为kε=6×10-2和Λ=1.3×105E,其中E为单位矩阵。
4.3 仿真对比
1)理想情况下的仿真对比
仿真对比FO-SMAC-NN 运行控制器和PID运行控制器控制下的列车运行性能,并从位置与速度跟踪效果、位置与速度跟踪误差、列车运行阻力估计效果及控制输出这4 个方面分析FO-SMACNN控制器的有效性。
设置参数:仿真时间取245 s,仿真步长取10-4s。中速磁浮列车在该仿真试验线上单程运行得到的期望速度-位置曲线如图3所示,单程运行距离为9.9 km。
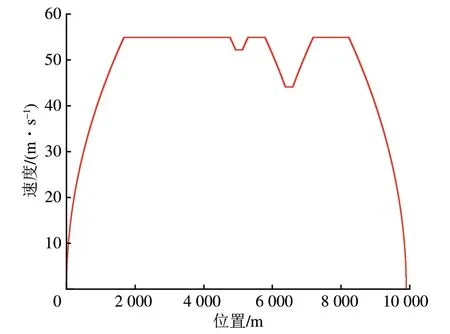
图3 中速磁浮列车试验线运行的期望速度-位置曲线
FO-SMAC-NN 运行控制器和PID 运行控制器对位置与速度的跟踪效果对比如图4所示。由图4可以看出:受运行阻力的影响,PID 运行控制器的位置与速度跟踪效果较差,在线路的坡道部分出现了较为明显的误差;FO-SMAC-NN 运行控制器由于补偿了列车运行阻力,在保障速度-位置曲线追踪精度的同时,速度曲线更为平滑。
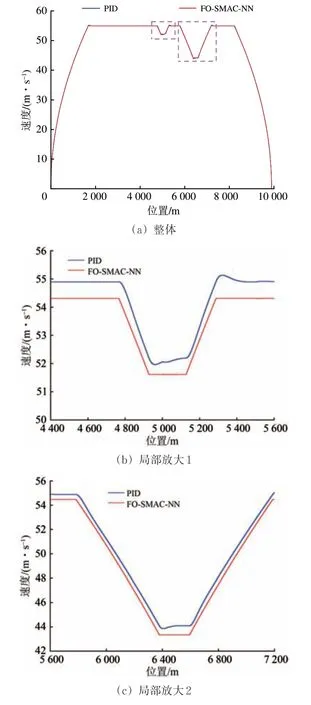
图4 FO-SMAC-NN 运行控制器和PID 运行控制器对位置与速度的跟踪效果对比
FO-SMAC-NN 运行控制器和PID 运行控制器的位置跟踪误差与速度跟踪误差分别如图5和图6所示,列车在试验线上运行的最大位置与速度跟踪误差见表3。综合图5、图6和表3可以看出:对于位置跟踪误差,FO-SMAC-NN 运行控制器在试验线全线上总体明显小于PID运行控制器,其位置跟踪性能更优;对于速度跟踪误差,在平直线路段,由于列车所受的运行阻力较小,FO-SMACNN 运行控制器对比PID 运行控制器的优势不明显,但在坡道线路段,FO-SMAC-NN 运行控制器补偿了运行阻力,有效降低了较大坡道附加阻力对列车运行的影响,表现出明显优于PID运行控制器的速度跟踪性能。

表3 FO-SMAC-NN 运行控制器和PID 运行控制器位置与速度的最大跟踪误差
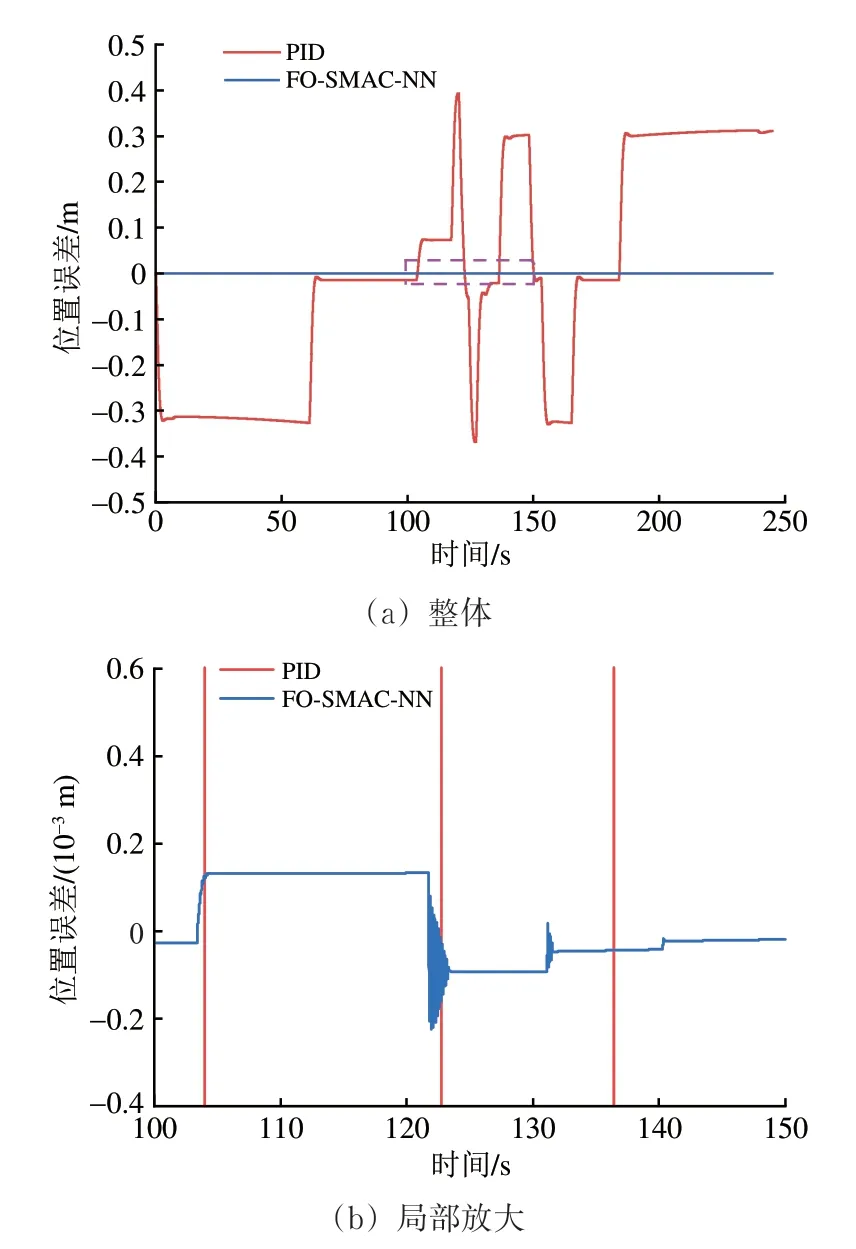
图5 FO-SMAC-NN 运行控制器和PID 运行控制器的位置跟踪误差对比
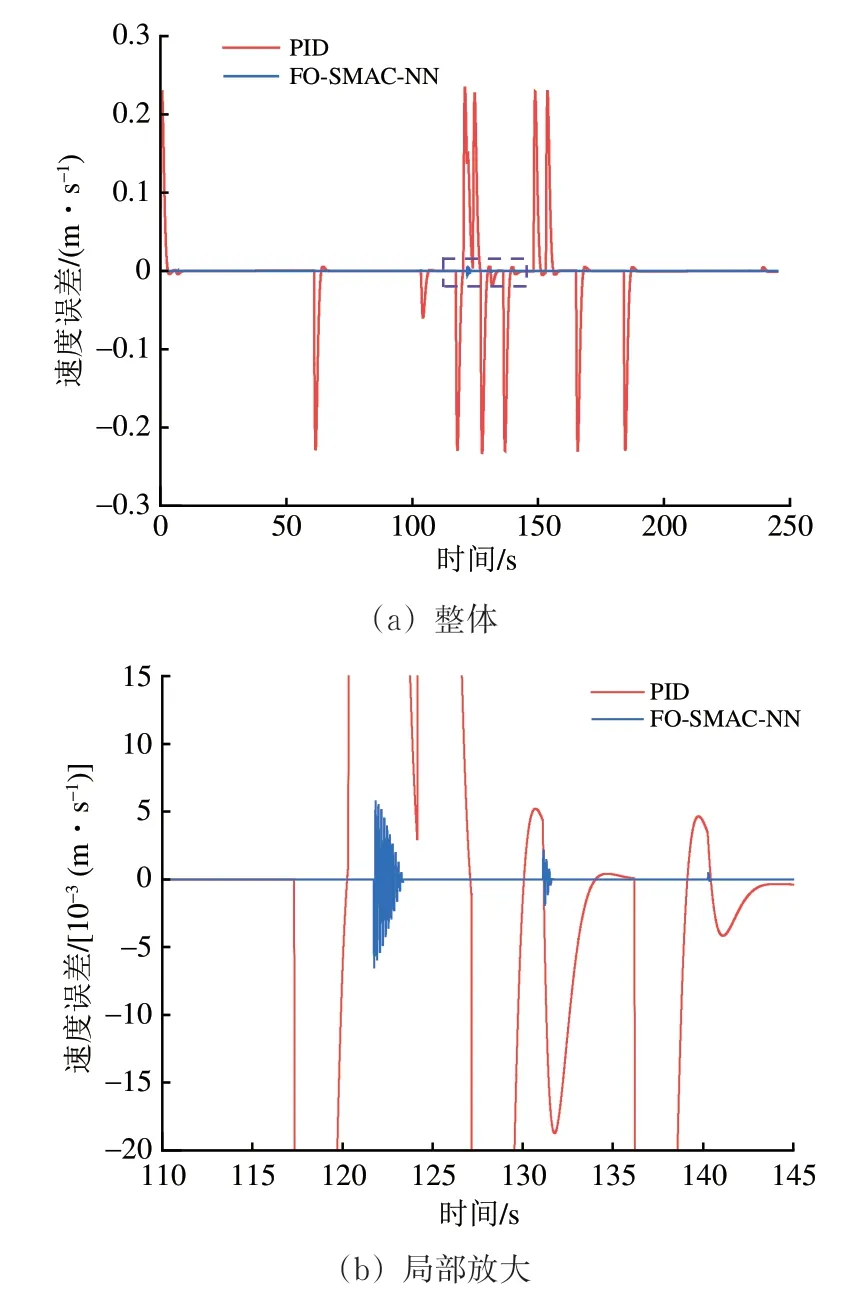
图6 FO-SMAC-NN 运行控制器和PID 运行控制器的速度跟踪误差对比
仿真时,设置的中速磁浮列车运行阻力以及FO-SMAC-NN 运行控制器估计得到的运行阻力如图7所示(PID 运行控制器无估计功能)。由图7可以看出,FO-SMAC-NN 运行控制器在整体上比较准确地估计了列车运行阻力,仅在运行阻力的突变部分产生了一定的抖动误差。
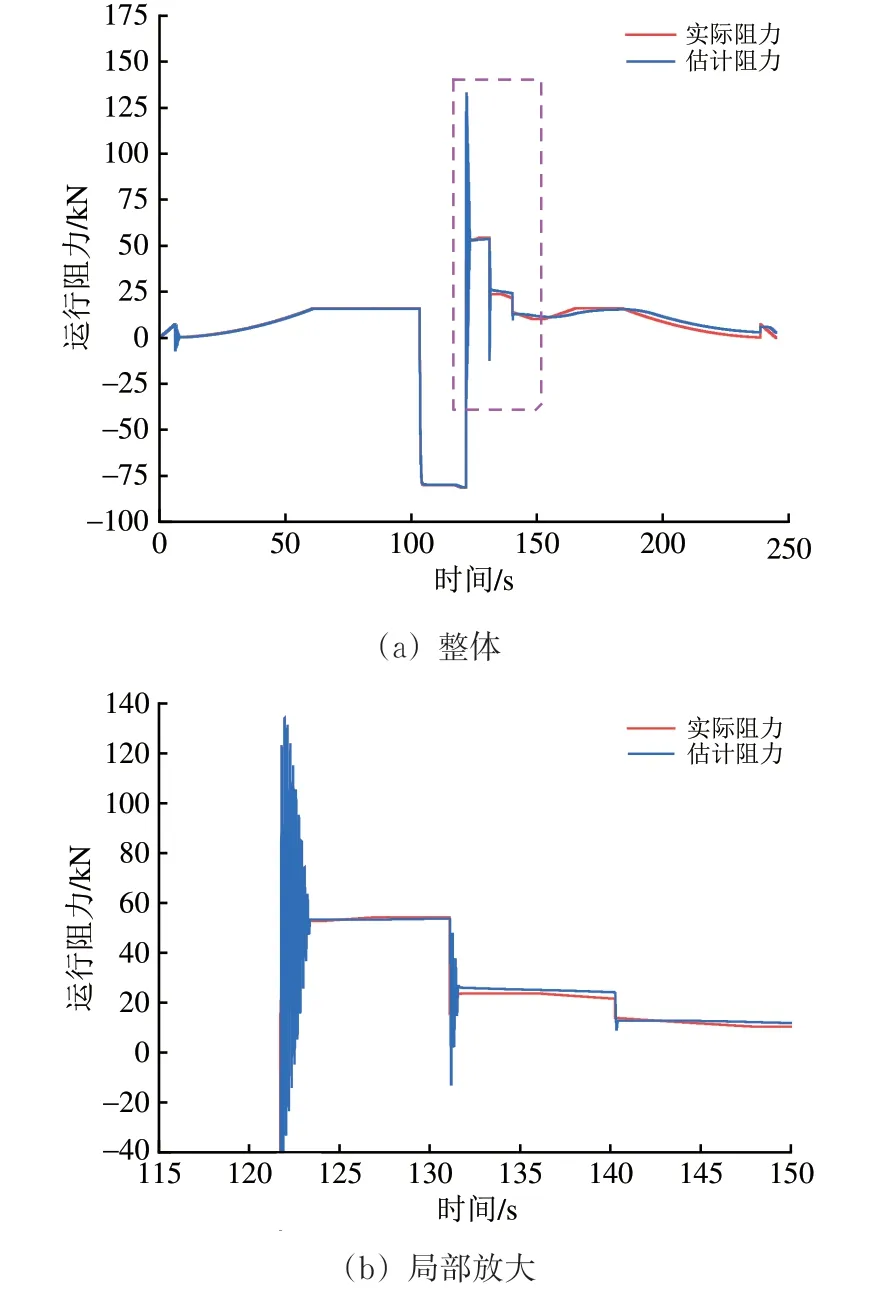
图7 FO-SMAC-NN运行控制器估计得到的列车运行阻力
FO-SMAC-NN 运行控制器和PID 运行控制器的控制输出曲线如图8所示。由图8可以看出,FO-SMAC-NN 运行控制器和PID 运行控制器得到的结果总体近似,但前者在输出力矩的突变部分更小且更加平滑。
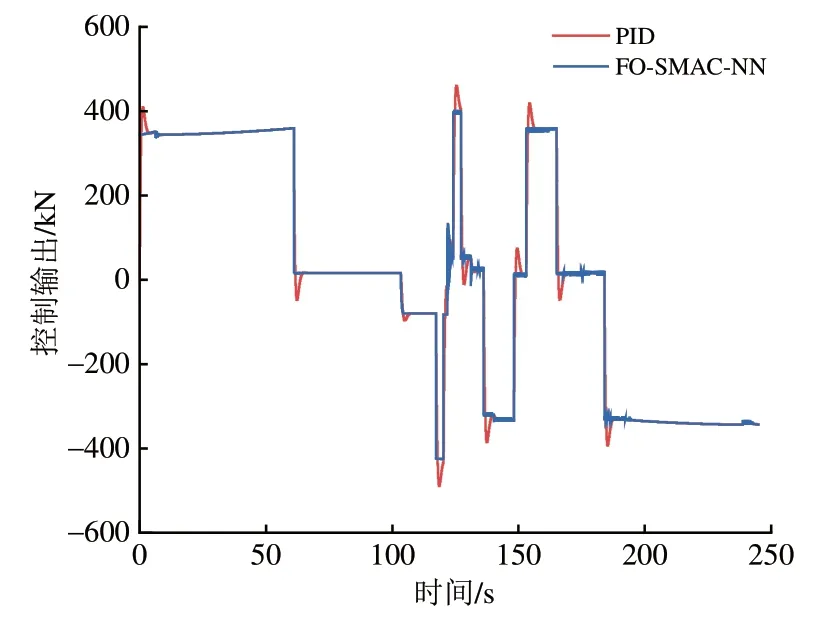
图8 FO-SMAC-NN 运行控制器与PID 运行控制器的控制输出对比
2)噪声干扰下的仿真对比
为了进一步验证本文所提出的FO-SMACNN 运行控制器的鲁棒性,在控制参数、试验线模型以及中速磁浮列车基本参数不变的情况下,加入功率谱密度为108的白噪声,得到的列车的位置与速度跟踪误差分别如图9和图10所示。由图9和图10 可以看出,尽管FO-SMAC-NN 运行控制器和PID 运行控制器的位置跟踪误差与速度跟踪误差均出现了抖动,但是前者在抖动幅度远小于后者的基础上表现出更小的位置与速度跟踪误差,进一步验证了FO-SMAC-NN 运行控制器鲁棒性较强的特点。

图9 噪声干扰下FO-SMAC-NN 运行控制器与PID 运行控制器的位置跟踪误差对比
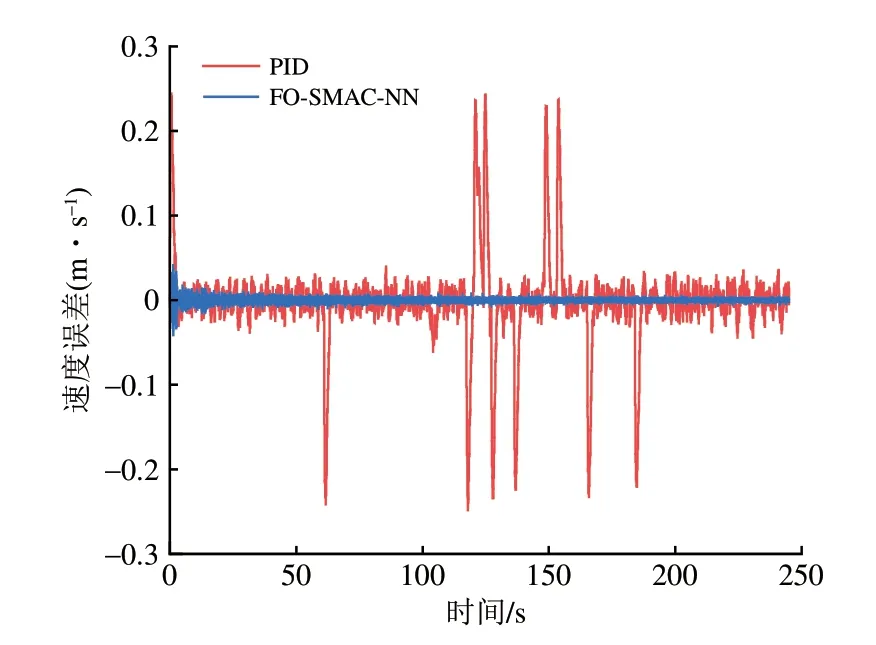
图10 噪声干扰下FO-SMAC-NN 运行控制器与PID 运行控制器的速度跟踪误差对比
5 结 语
本文针对中速磁浮列车运行阻力对运行控制的不利影响,考虑中速磁浮交通对运行控制的高精度与强鲁棒性要求,基于构造的中速磁浮列车动力学方程,设计了基于分数阶滑模自适应神经网络(FO-SMAC-NN)的运行控制器,通过产生牵引力或制动力的形式控制列车运行。控制器主要结构包括3个部分:速度前馈部分能够改善系统的瞬态响应;分数阶滑模自适应等效控制部分能够保证列车控制系统满足基本的控制要求;自适应神经网络阻力补偿部分根据列车运行误差信息,通过神经网络实时估计并补偿列车运行阻力,抑制运行阻力对列车运行的影响,提高列车运行控制性能。根据李雅普诺夫稳定性定理,证明了采用该运行控制器的闭环控制系统能够保障中速磁浮列车的稳定运行。分别在理想情况和功率谱密度为108的白噪声干扰情况下进行仿真,证实了FO-SMAC-NN 运行控制器可以准确估计中速磁浮列车运行阻力,并产生相应的补偿控制力矩;与传统的PID运行控制器相比,结合了分数阶控制、滑模自适应控制以及神经网络的FO-SMAC-NN 运行控制器还进一步增强了运行控制系统的控制精度与鲁棒性,提高了运行控制系统对列车位置与速度的跟踪性能。

