基于Ginigram和CHMR的列车轴箱轴承早期故障自主识别方法

辛 格，钟槭畑，李 哲，贾利民，杨 洋，李林峰

（1. 北京交通大学交通运输学院，北京 100044；2. 北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044；3. 北京交通大学轨道交通控制与安全国家重点实验室，北京 100044；4. 中车唐山机车车辆有限公司，河北唐山 063000；5. 北京电子工程总体研究所，北京 100854）

随着轨道交通的快速发展，列车设备的自动化、智能化程度越来越高，对设备运行的安全性、可靠性也提出了更高要求。作为故障预测和健康管理的重要组成部分［1］，故障诊断技术能够有效防止安全事故的发生，近年来在学术研究和工程实践中成为热点［2-3］。轴承是列车的基础部件，同时也是易损部件，其健康状态在确保列车安全运行中起着关键作用［4］。在工程中，列车轴箱轴承常常处于高转速、重载荷等恶劣工作环境，极易诱发损伤，成为影响列车可靠安全运行的主要隐患之一［5］。因此，针对列车轴箱轴承的自主故障识别，不仅能有效保障列车安全运行，还能实现列车轴箱轴承的智能化诊断，促进列车修制由“计划修”向“状态修”转变，为运营单位降本增效提供技术支持。

信号处理技术能检测出隐藏在振动信号中的周期性冲击频率（即故障特征频率），从而准确识别轴承的故障类型。现有振动信号处理方法主要包含2 类：一类是基于振动信号稳态或近似稳态假设的各种经典信号处理方法［6］；另一类是针对非稳态信号特征提取的方法，如小波变换［7］、经验模态分解［8］和包络分析（Envelope Analysis， EA）［9］等，其中，EA 被工业界广泛采用，并被证实是行之有效的方法。然而，直接将EA 应用于列车轴箱轴承故障诊断和在途监测，仍有2 个亟待解决的实际问题：①多信号源混叠问题，列车的运行环境复杂，振动信号中存在背景噪声信号、随机脉冲信号和故障信号混叠现象，EA 对低信噪比的早期微弱故障信号诊断效果不理想；②早期故障程度无法量化问题，目前大多数故障诊断方法仍需人为地分析故障特征才能确定故障部位和故障程度信息，对使用者的专业知识和工作经验要求较高，给工程应用带来极大困难。

针对多信号源混叠问题，谱峭度（Spectral Kurtosis， SK）能够有效检测轴承故障信号的非高斯性，因而被用来检测信号中的故障特征［10］。为了解决SK 计算效率低的问题，Antoni 将1/3-二叉树滤波器组与SK 结合提出Kurtogram 方法［11］，通过快速计算SK 有效提取信噪比最优的频段，从而实现微弱故障特征的提取。然而，由于SK 对随机脉冲信号过于敏感，Kurtogram 方法在对存在随机脉冲信号干扰时的故障特征提取效果并不理想，针对该问题Barszcz 等提出Protrugram 方法，提高了SK 的频率分辨率和检测效果，但是其带宽需要预先设定［12］。随着研究的深入，Antoni 通过引入谱负熵（Spectral Negentropy）提出了信息图（In⁃fogram）方法［13］。虽然上述方法可以有效提取最优故障特征频段的故障信号，但是没有考虑列车轴承振动信号中强随机脉冲信号对故障诊断的影响，并且还需要经过专业的人工分析才能获知准确的轴承故障部位和故障程度信息。

针对早期故障程度无法量化问题，目前的一个主要思路是通过相关指标量化包络谱中包含的故障特征。Borghesani 等［14］和Smith 等［15］分别提出循环分量比和二阶循环平稳指标，通过这2 个指标计算平方包络谱（Squared Envelope Spectrum，SES）中轴承故障特征频率对应的峰值谱线识别故障发生的部位，但是这2 个指标在用于故障特征识别时计算的频段过宽，倍频计算数量也过少。随后，Kass等［16］基于增强包络谱（Enhanced Envelope Spec⁃trum，EES）提出故障出现率，对故障特征的识别频段宽度和倍频计算数量进行了改进，但是在计算时并没有考虑多信号源混叠的情况。此外，上述3个指标均未考虑轴承内圈和滚动体故障特征中边频的影响。

本文针对多信号源混叠问题，将1/3-二叉树滤波方法与基尼系数结合形成Ginigram 方法，通过识别故障特征所在的最优解调频段，以有效地从背景噪声、随机脉冲等干扰信号中提取出故障特征；针对早期故障程度量化问题，基于预处理信号的SES，提出采用循环谐波中值比（Cyclic har⁃monic-to-median ratio，CHMR）这一统计指标以量化轴承故障部位和故障程度信息，进而基于CHMR，根据正态分布的西格玛原则提出了故障分级准则，实现列车轴承早期故障程度的自动量化。采用提出的基于Ginigram 和CHMR 的列车轴箱轴承自主故障识别方法，试验验证了其有效性。

1 基于Ginigram的信号预处理

Kurtogram 方法使用的峭度对单个强脉冲信号非常敏感，当信号存在单个强脉冲信号和周期性故障信号混叠情况时可能会导致误检，而基尼系数对信号中的随机强脉冲信号具有很好的抗性［17］，因此，采用对随机脉冲信号不敏感同时能够测量故障特征的基尼系数对Kurtogram 方法中的峭度进行替换，具体思路如图1所示。图1中，轴承振动加速度信号被1/3-二叉树分解为多个等级和频段，其中，每个等级包括2k（k为分解等级）个频段，通过计算各个频段包络信号的基尼系数，选取基尼系数最大的频段作为最优滤波频段，为区别于Kurto⁃gram，称其为Ginigram。

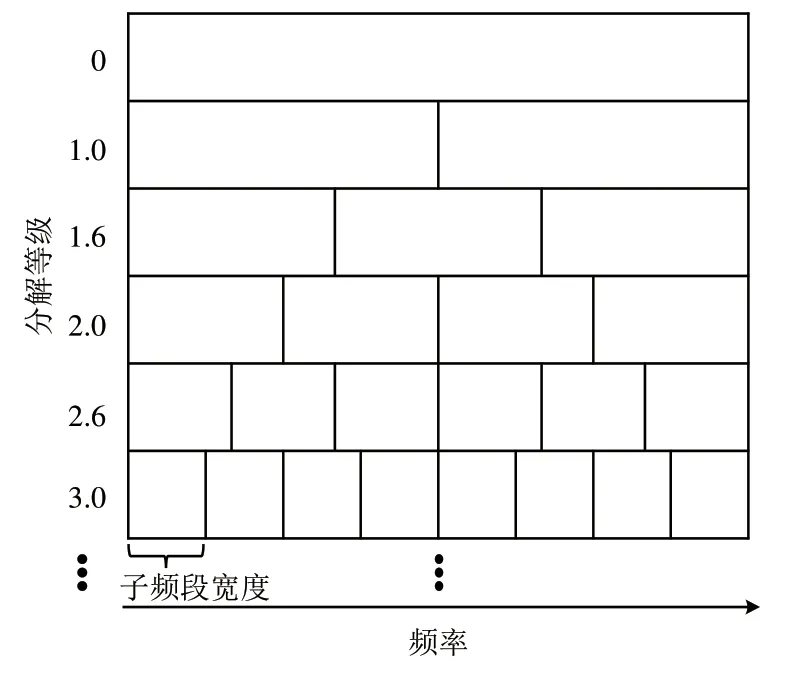
图1 Ginigram计算思路

具体地，基尼系数的定义为

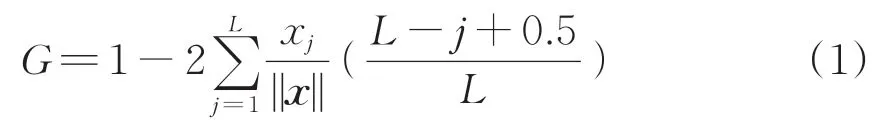
其中，

x=(x1x2…xL)

式中：G为基尼系数的值；x为振动加速度信号xj按幅值从小到大排序的向量；L为向量x的总长；||x||为x所有幅值的绝对值之和。

根据Ginigram 方法得到x的最优滤波频段[fl，fh]，其中，fl和fh为最优滤波频段的下限和上限。基于最优滤波频段[fl，fh]对轴承振动加速度信号进行带通滤波得到滤波信号xb。为进一步分析滤波信号xb的SES，需先计算滤波信号xb的解析信号，为

式中：为解析信号；j 为复数单位；H(·)为希尔伯特变换。

然后基于解析信号的幅值计算SES，为

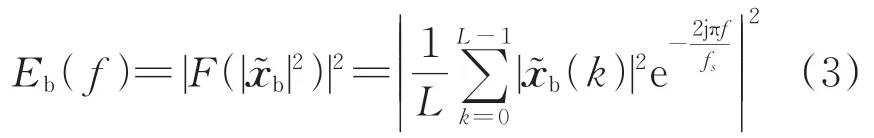
式中：Eb(f)为SES在频率f处的幅值；为的第k个值；F(·)为离散傅里叶变换；fs为信号的采样频率。

SES 中包含了故障特征的频率和幅值信息，为自主识别SES 的故障特征，需要提出量化指标对SES的故障特征进行有效提取。

2 基于CHMR的故障程度量化

针对故障程度量化问题，基于预处理信号的SES 建立二元假设模型，采用CHMR 以量化SES中所包含的故障部位及故障程度信息。

2.1 基于SES/EES的故障程度量化经典指标

目前，故障程度量化指标的思路是在信号SES/EES 的频域内通过窄频段识别故障轴承的特征频率和高次倍频，以提取故障特征幅值。经典的量化指标包括循环分量比［14］、二阶循环平稳指标［15］和故障出现率［16］。

1）循环分量比

Borghesani 等［14］基于SES 提出了循环分量比（Ratio of Cyclic Content，RCC），其定义如下。

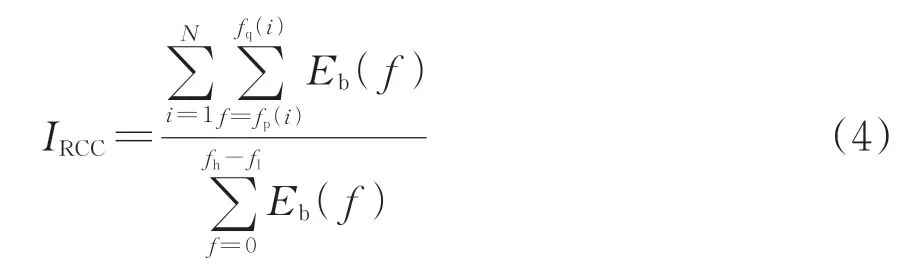
式中：IRCC为SES 窄频段内幅值之和与SES 所有幅值之和的比值，即循环分量比；N为窄频段倍频的计算数量；fp(i)和fq(i)分别为第i个窄频段的下限和上限。

2）二阶循环平稳指标

Smith 等［15］基于SES 提出了二阶循环平稳指标（Indicator of Second-Order Cyclostationarity，ICS2），其定义如下。

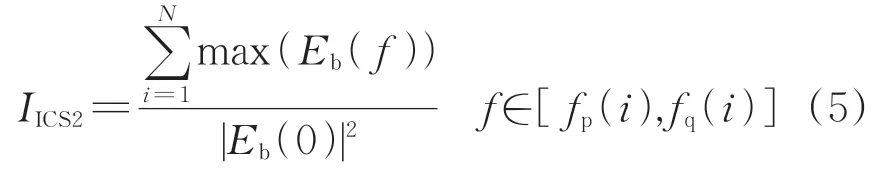
式中：IICS2为窄频段内幅值的最大值与SES 中0 频率对应幅值的比值，即二阶循环平稳指标；max(·)为求最大值运算。

3）故障出现率

由于RCC 和ICS2 对于窄频段宽度的选取精度较低，Kass 等［16］基于EES 提出了故障出现率（Probability of Presence of a Fault，PPF），其定义如下。

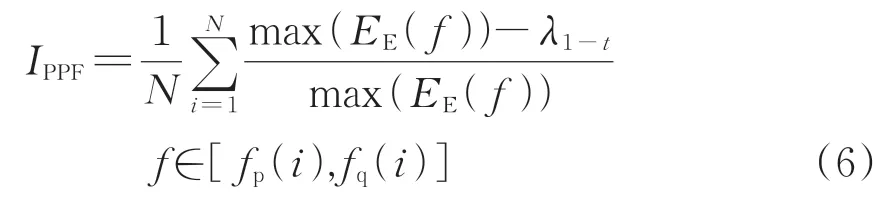
式中：IPPF为EES 窄频段内幅值的最大值减去阈值λ1-t（λ1-t为EES 的直方图100(1-t)%分位点对应的数值，t为显著性水平）之后与EES 最大值的比值，即故障出现率；EE(f)为EES 在频率f处的幅值。

上述3 个经典指标通过SES/EES 实现了轴承故障信息的量化，然而针对列车轴箱轴承复杂恶劣工况下的故障自主识别问题，依然存在一定局限性：①RCC 和ICS2 未考虑设置噪声阈值，增加了误报风险；②RCC 的窄频段过宽，易识别一些非故障特征频率幅值；③RCC 和ICS2 的窄频段计算数量过少，未充分考虑故障特征的谐波特性；④3种指标均未考虑内圈和滚动体边频故障特征的影响；⑤PPF 未进行滤波处理，存在故障特征的漏报风险。

2.2 基于SES的CHMR

针对3 个经典量化指标存在的不足进行改进，并更进一步考虑噪声对故障特征量化的影响从而估计噪声阈值，降低噪声对故障特征量化的影响。

1）阈值计算和CHMR设计

针对噪声阈值的计算问题，建立基于SES 的二元假设模型，为

根据文献［9］，可得二元模型的判决统计量θ(f)为

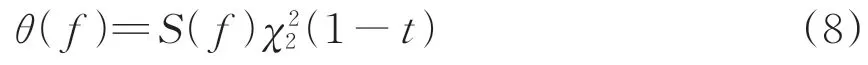
式中：S(f)为尺度因子；χ22(1-t)为二自由度卡方分布的累计概率密度函数。

S(f)可由下式进行估计，估计结果(f)为

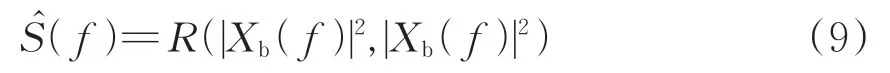
式中：R(·)为互相关运算；Xb(f)为滤波信号xb的离散傅里叶变换结果。

由式（8）可知：如果Eb(f)＞θ(f)，拒绝H0假设，接受H1假设，即SES包含故障特征；反之，接受H0假设，即SES 不包含故障特征。因此，将θ(f)作为区分2种假设模型的判断阈值。

设置阈值主要包含2 个方面作用：①根据阈值精确判断SES 中窄频段的峰值是否为故障特征；②对峰值的连续性进行识别，确保从各个窄频段内识别到的峰值均超过阈值，以对应故障机理中的谐波特性。

基于此，提出一种新指标CHMR，以量化轴承故障部位和故障程度信息，计算公式如下。

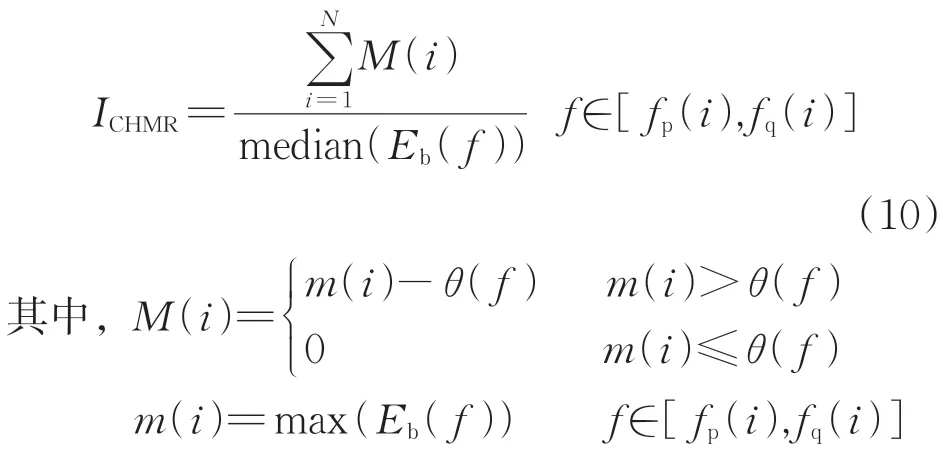
式中：ICHMR为SES 窄频段内最大值减去阈值后与SES 中位数的比值，即循环谐波中值比；median(·)为求中位数运算；m(i)为第i个窄频段内识别的峰值；M(i)为在第i个窄频段内识别的峰值经阈值处理后的值。

2）窄频段宽度计算

针对窄频段宽度设置，经典指标始终基于故障特征频率和其倍频取定值，与之不同，本文选取第1 个窄频段峰值估计的故障特征频率作为高次倍频和窄频段的计算基准以减少计算误差，则式（10）的窄频段下限和上限为

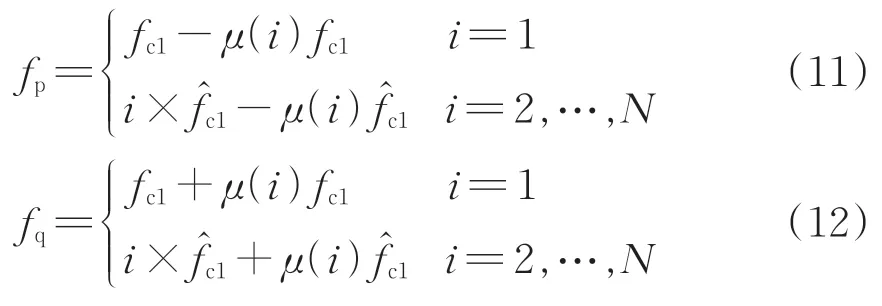
式中：fc1为预估的故障特征频率；为第1 个窄频段内识别的峰值对应的频率；μ(i)为第i个窄频段的误差系数。

根据轴承动态特性，随机滑动会造成故障特征频率与理论值存在2%左右的误差［18］。此外，考虑到工程应用的复杂性，将第1个窄频段的误差系数设置高于2%。因此，μ(i)的取值为

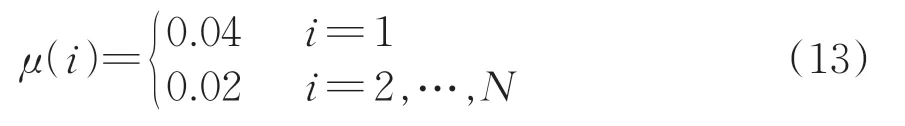
3）窄频段数量设置

包络谱中观察到故障特征频率及谐波出现3～5 个连续的高幅值时可确定轴承的故障特征［12］。不同于RCC 和ICS2 只计算1 个窄频段，本文选择计算外圈、内圈、保持架故障的窄频段，即计算数量为N=3，特别地，考虑到滚动体故障特征偶次谐波的峰值比奇次谐波的峰值更明显［18］，其窄频段计算数量应设为偶数，所以滚动体故障的窄频段计算数量取N=4。

4）故障特征边频段计算

轴承的内圈和滚动体故障信号存在周期性振幅调制现象，而经典指标未考虑内圈和滚动体的边频调制特征。因此，本文根据调制原理，在内圈的故障特征频率基础上分别加上和减去轴的转频；滚动体故障特征频率分别加上和减去保持架故障特征频率。因此，对于内圈、滚动体故障，CHMR 的计算式为

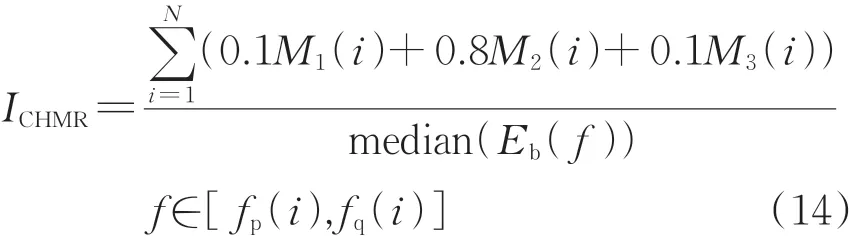
式中：M1(i)，M2(i)，M3(i)分别为由左侧边频段，中间主频段，右侧边频段识别出的故障特征峰值。

综上，CHMR 与3 个经典指标的异同点如图2所示。与3 个经典指标相比，CHMR 的优势在于：①考虑了噪声阈值，并选取中位数作为基准，能有效降低噪声对故障特征量化的干扰；②考虑到轴承随机滑动的影响，进一步优化了窄频段设置的宽度；③针对轴承各个部位的不同故障特性设置了窄频段的计算数量；④对内圈和滚动体的边频故障特征进行了加权计算。

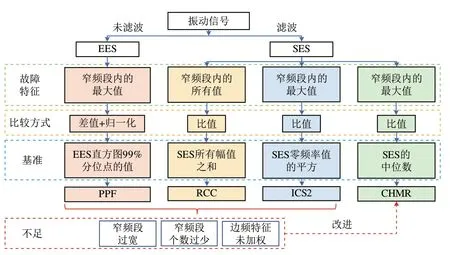
图2 CHMR与3个经典指标的异同点

2.3 故障部位识别与故障分级

利用轴承在正常运行状态下的历史数据来计算CHMR 的3σ区间(μ-3σ，μ+3σ)，其中μ为CHMR 的均值，σ为CHMR 的标准差。根据3σ法则：数值落在区间(μ-3σ，μ+3σ)外的事件为极小概率事件，即在实际中基本不可能发生。因为轴承发生故障时CHMR 较健康状态将会增大，故将健康轴承CHMR 的μ+3σ值作为健康阈值，根据历史健康数据计算阈值，对未知数据各个部位的CHMR 进行检测，实现故障特征的自主识别。此外，根据不同故障程度轴承测量数据可以实现各级故障的阈值计算，实现轴承故障程度分级，本文根据轴承故障程度将轴承故障分为无故障、轻微、中等和严重故障共4 段等级。轴承故障时的CHMR值会明显升高，因此根据西格玛准则选取健康轴承CHMR 的μ+3σ值作为1 级阈值（即健康阈值），轻微故障CHMR 的μ+3σ值或中度故障CHMR 的μ-3σ值（如果同时有轻微和中等故障数据，取轻微和中等故障CHMR 的均值）作为2 级阈值，中度故障CHMR 的μ+3σ值或重度故障CHMR 的μ-3σ值作为3 级阈值（如果同时有中等和严重故障数据，取中等和严重故障CHMR 的均值）。CHMR 低于1 级阈值时，视轴承为无故障；高于1级阈值低于2 级阈值，视轴承为轻微故障；高于2级阈值低于3 级阈值，视轴承为中等故障；高于3级阈值，视轴承为严重故障。通过上述方法，得到3级阈值并实现轴承状态的4段划分，称其为“3级4段制”轴承状态分级法。

3 早期故障自主识别流程

综上所述，基于Ginigram 方法和CHMR 的列车轴箱轴承自主故障识别方法流程如图3所示。首先，轴承振动加速度信号经Ginigram 进行滤波，并计算滤波信号的SES；然后，基于滤波信号的SES 计算CHMR，并根据西格玛原则计算CHMR的阈值以识别故障样本；最终，基于历史的健康和故障数据计算故障分级阈值以实现轴承故障分级。

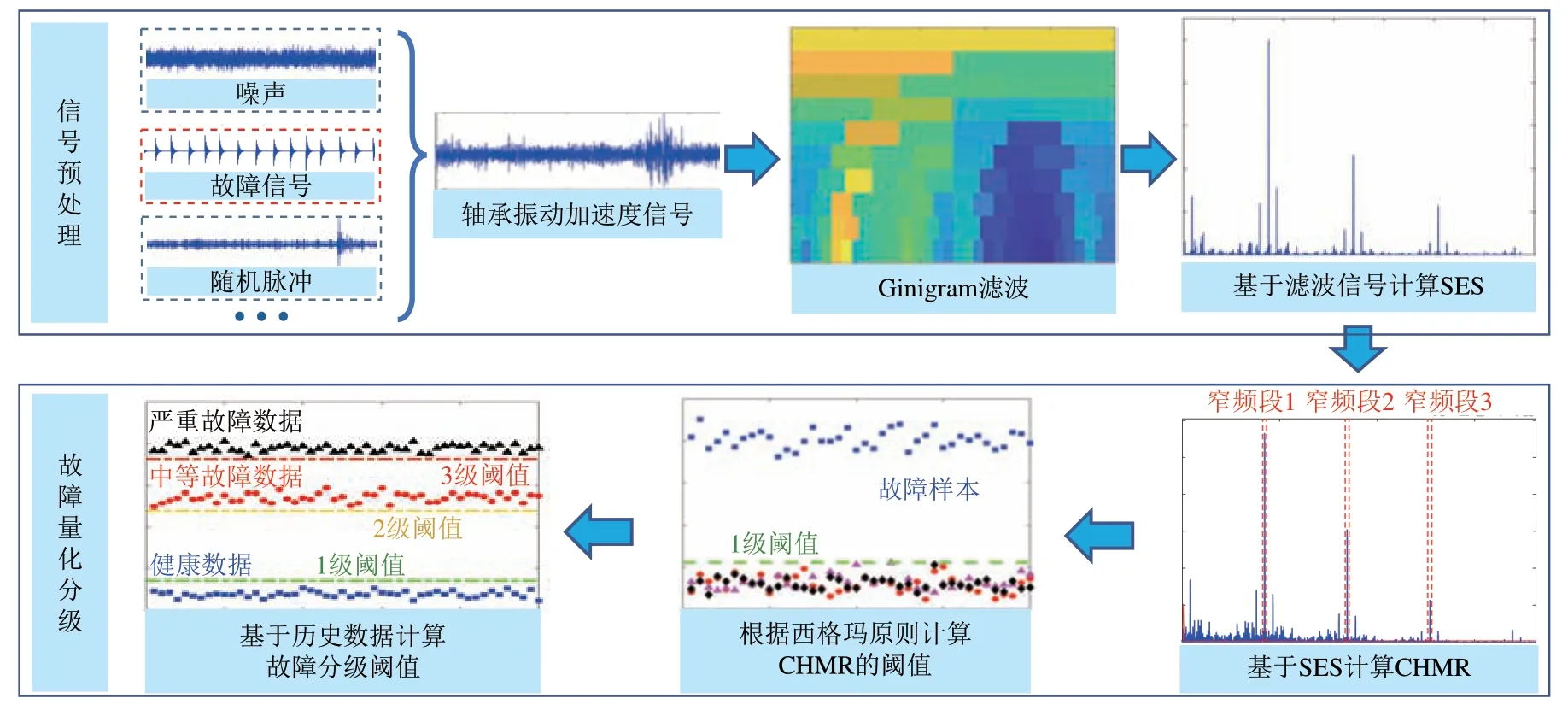
图3 基于Ginigram和CHMR的自主故障识别方法流程图

4 试验验证

4.1 列车轴箱轴承试验台

列车轴箱轴承的真实振动数据是对所提方法进行验证、对比、优化的重要依据。然而，实际运行列车的轴承振动数据存在故障样本稀缺的问题。为了获取尽可能接近实际运行状态的列车故障轴承振动数据，试验中使用了从列车轴箱上拆卸下来的自然磨损的早期故障轴承，并将其装配到与列车轴箱等比例的列车轴箱轴承试验台上进行原始振动信号的采集。

列车轴箱轴承试验台包括驱动端电机、风扇端电机、传动装置、轴箱轴承以及横向和垂向载荷装置，如图4所示。其中，轴箱轴承装配在车轴2端，载荷装置可以模拟列车实际运行期间轴承所承受的不同方向载荷。电机的功率为75 kW，转速最高可达1 480 r·min-1，可实现无级调速，配合载荷装置可以开展列车在不同车速和不同工况下的试验。振动加速度传感器安装在轴箱的12 点钟方向（垂向）。试验中使用的轴承参数见表1。

图4 列车轴箱轴承试验台

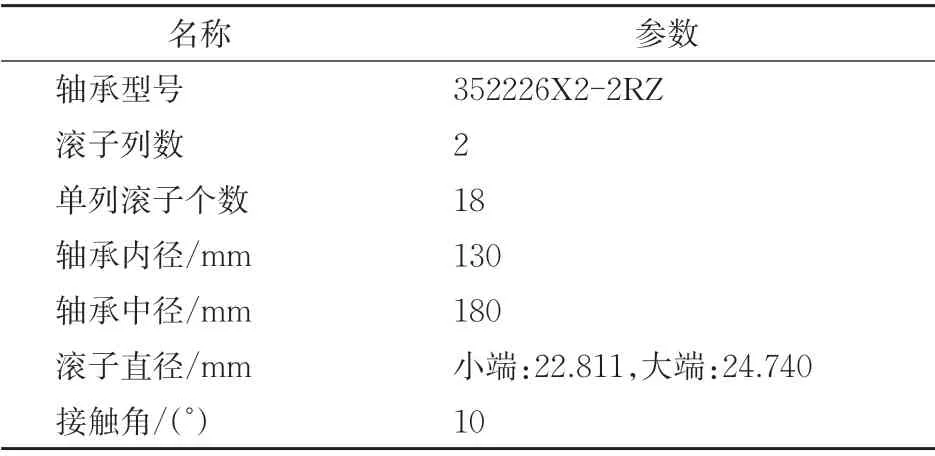
表1 试验轴承参数

区分各个轴承的故障程度时，由于内外圈和滚动体磨损对轴承故障的影响程度不同，将外圈和内圈磨损面积小于300 mm2的故障定义为轻微故障，磨损面积大于450 mm2的故障定义为严重故障，磨损面积在轻微故障和严重故障磨损面积之间的故障定义为中等故障。滚动体较内、外圈滚道表面积更小，定义磨损面积50 mm2以下的为轻微故障，磨损面积100 mm2（不含100 mm2）以上的为严重故障，磨损面积在轻微故障和严重故障磨损面积之间的为中等故障。列车故障轴承的实物如图5所示，对应的轴承磨损程度信息见表2。

图5 列车故障轴承

表2 列车故障轴承磨损程度信息

4.2 Ginigram 方法有效性验证试验

为了验证Ginigram 方法的有效性，选择更接近工程实际的多信号源混叠案例进行对比验证。在模拟列车以90 km·h-1速度行驶、施加垂向载荷为56 kN 的工况下，采集外圈故障轴承的原始信号，采样频率为37 268 Hz、时长为10 s，结果如图6所示。图中：故障脉冲仅挑选4 处作为示意。由图6可知：该信号包含了强随机脉冲、微弱外圈故障脉冲和背景噪声信号，对应的外圈故障特征频率为64.52 Hz。

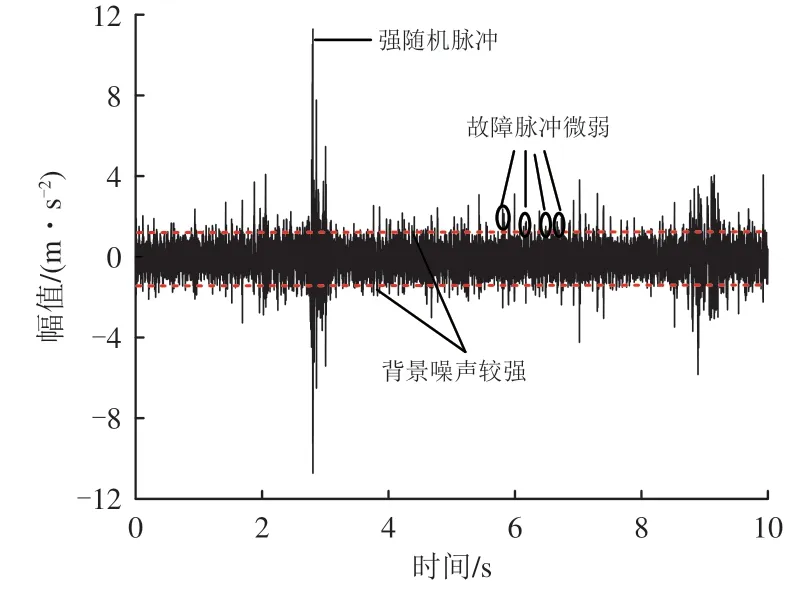
图6 外圈故障轴承原始振动加速度信号时域波形

采用经典的Kurtogram 和Ginigram 分别对图6所示原始信号进行滤波处理，结果如图7所示。图中：红色方框标出的为最优滤波频段。由图7可知：Kurtogram 中最大峭度对应的最佳滤波频段为第5 等级，中心频率4 351.9 Hz，带宽512 Hz，最大峭度为101.9，而Ginigram 中最大基尼系数对应的最佳滤波频段在第5 等级，中心频率为2 815.9 Hz，带宽512 Hz，最大基尼系数为0.5，这说明在故障信号中包含强脉冲干扰的情况下，Ginigram 和Kurtogram识别的最优频段不一致。

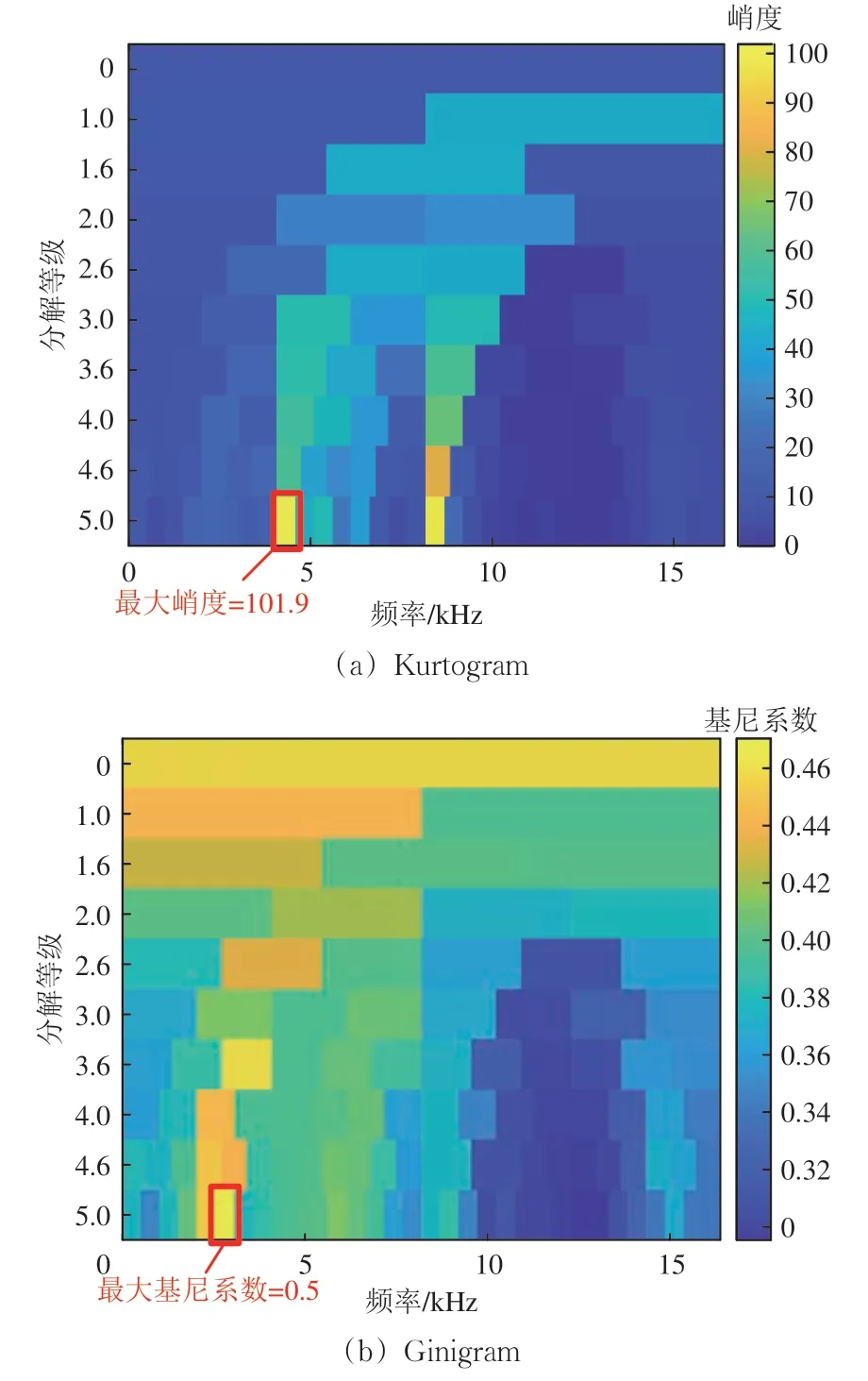
图7 Kurtogram和Ginigram最优滤波频段对比

分别计算图6所示原始信号以及图7所示最优频段滤波信号的SES，对比分析结果如图8所示。由图8可知：受多信号源混叠的影响，原始信号的SES 无法观察到故障特征；虽然Kurtogram 方法预处理后信号的SES 中包含故障特征，但其峰值的谱线受噪声干扰严重；而Ginigram 方法预处理后信号的SES 能清晰地呈现出故障特征谱线且噪声干扰微小；对比结果证明，Ginigram 方法相较于Kurtogram 方法能够更好地从多信号源混叠信号中选取最优信噪比频段，更适合做进一步的故障信息量化。

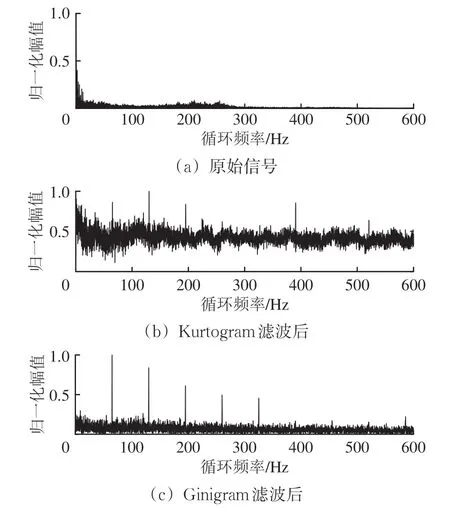
图8 原始信号及Kurtogram 和Ginigram 滤波后信号的SES对比

4.3 CHMR有效性验证试验

1）数据采集与参数设置

在模拟列车以时速90 km 行驶、施加垂向载荷为56 kN 的工况下，通过列车轴箱轴承试验台对健康轴承及1 号—6 号故障轴承各采集1 组振动数据，采样频率为32 768 Hz，每组采集90 个样本，每个样本采样时长为1 s。

在比较CHMR 与3 个经典指标时，为保证公平性，所有指标均采用Ginigram 方法对信号预处理后进行计算。窄频段及边频段的计算数量和宽度根据式（11）—式（14）计算。

2）故障部位自主识别能力验证

为验证CHMR 的故障部位识别能力，设置CHMR与3个经典指标的故障部位识别能力对比试验。根据西格玛原则计算阈值，对各组故障数据进行故障部位识别，并按如下规则计算准确率：由数据计算的指标超出健康阈值即为对应部位存在故障，如识别结果与实际故障部位相符，且其他部位未发生误报，则为识别准确；反之，均视为不准确。

对1 号—6 号轴承分别按上述标准计算故障部位识别准确率，测试结果见表3。由表3可知：总体上，CHMR 和PPF 的准确率较RCC 和ICS2 更高，且CHMR 对5 号轴承故障部位的识别表现最优。上述试验表明，CHMR 对于轴承故障部位的自主识别能力明显优于RCC 和ICS2，略优于PPF。

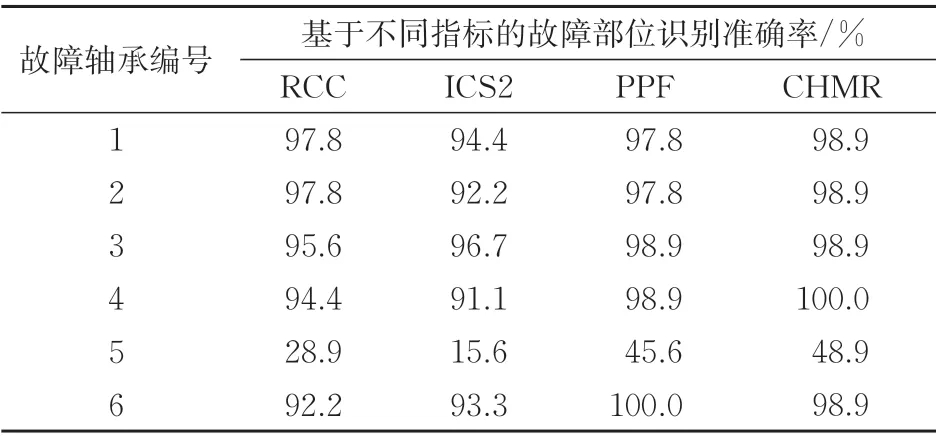
表3 指标故障部位识别准确率

3）故障程度区分能力验证

为验证CHMR 对故障程度的区分能力，分别比较CHMR 与3 个经典指标对于外圈、内圈、滚动体3个部位的故障程度区分效果。

对于外圈故障，选取健康轴承、1 号（外圈中等故障）和2 号（外圈严重故障）轴承的各50 个数据样本进行对比试验，结果如图9所示。由图9可知：4 种指标均能明显区分轴承的健康与故障状态，然而，RCC 和PPF 对外圈的故障程度难以区分，ICS2 仅能区分出部分样本，而CHMR 能够清晰完整地区分轴承的故障程度。

对于内圈故障，选取健康轴承、3 号（内圈中等故障）和4号（内圈严重故障）轴承的各50个数据样本进行对比试验，结果与图9相似，限于篇幅未列出。结果表明，RCC 和PPF 很难区分故障程度，ICS2 能够区分部分样本，而CHMR 区分效果最好。

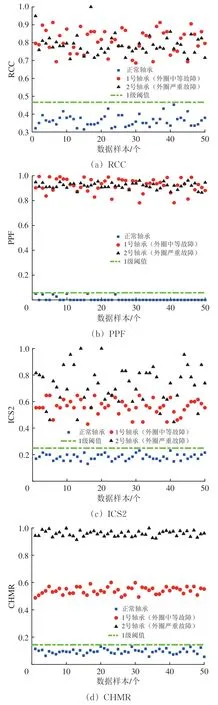
图9 基于不同指标的外圈故障程度区分结果

对于滚动体故障，选取健康轴承、5 号（滚动体轻微故障）和6号（滚动体严重故障）轴承的各50个数据样本进行对比试验，结果如图10所示。

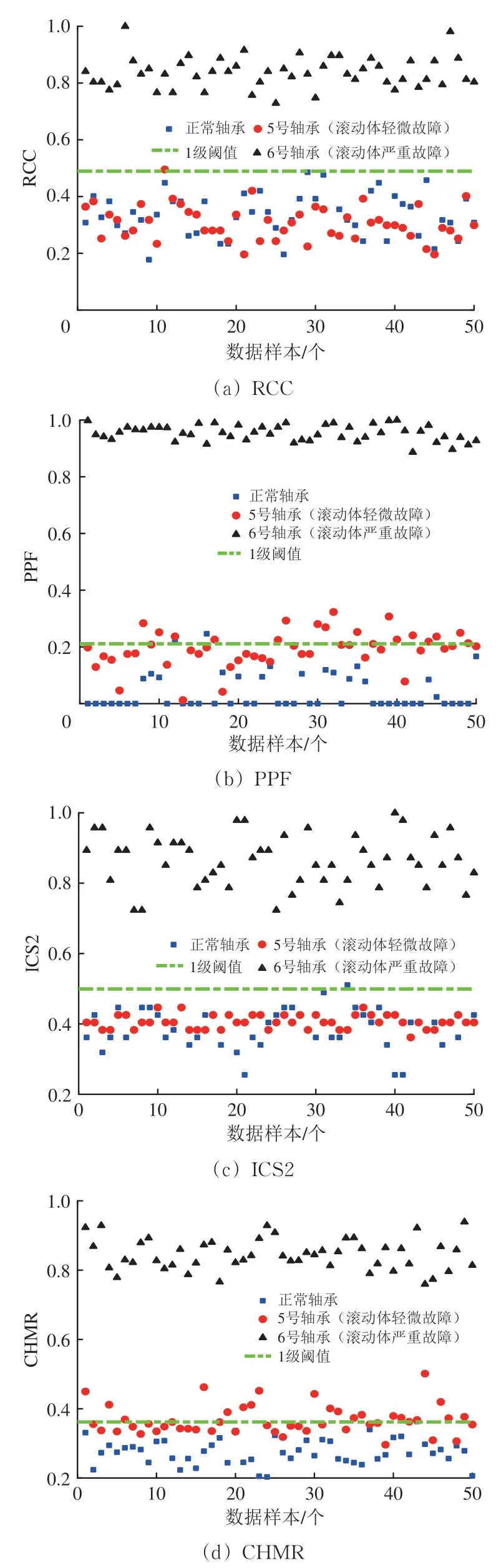
图10 基于不同指标的滚动体故障程度区分结果

由图10 可知：4 种指标均能明显区分出6 号轴承的故障；不同于外圈和内圈的区分结果，对于5号轴承故障，由于其剥落面积过小（见图5（e）），各个指标对5号轴承的故障识别效果不如6号轴承；具体地，RCC 和ICS2 指标均无法对5 号轴承进行故障状态与健康状态区分，仅PPF 和CHMR 能够部分区分上述2 种状态，且CHMR 区分效果更好。

综上所述，相较于3 个经典指标，提出的CHMR 在列车轴箱轴承故障程度区分能力上更具优势，更适用于轴承故障程度的自主识别。

4.4 基于西格玛原则的故障分级

根据西格玛原则，基于现有的试验数据，可以进一步自主辨识故障等级。以轴承外圈故障为例，根据“3 级4 段制”状态分级法，分别计算外圈轴承的1 级阈值、2 级阈值和3 级阈值，结果如图11所示。对于新的数据样本，首先计算CHMR，然后与现有分级阈值比较，超过1 级阈值而不超过2级阈值，判断轴承处于亚健康状态，需要持续地对轴承进行监测；超过2 级阈值而不超过3 级阈值，判断轴承处于中度故障状态，需要在一定时间内安排维修作业；超过3级阈值，判断轴承处于严重故障状态，需要尽快对轴承采取维修措施。“3级4段制”状态分级法的优势在于能够从统计的角度量化轴承的状态区间，进而设定划分故障等级的阈值，实现数据驱动的列车轴箱轴承故障程度分级。

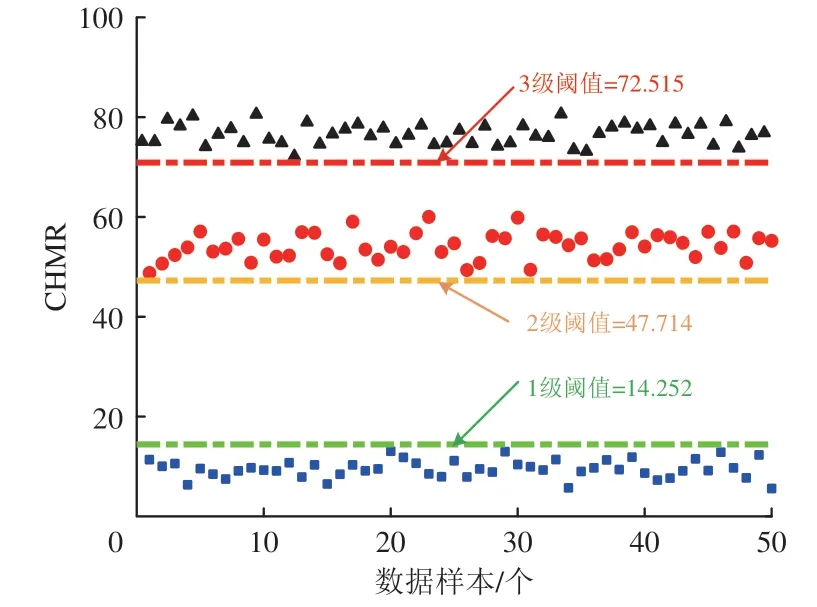
图11 列车轴箱轴承“3级4段制”状态分级法

5 结 论

（1）针对多信号源混叠问题，提出能够有效地从多源混叠的原始振动信号中快速选取最优滤波频段的Ginigram 方法；针对故障程度量化问题，基于Ginigram 方法滤波信号的SES 建立了二元假设模型，进而提出能够自主识别轴承故障部位和量化轴承故障程度的CHMR，并由CHMR 的统计特性和西格玛原则提出列车轴箱轴承“3 级4 段制”状态分级方法。

（2）Ginigram 方法相较于Kurtogram 方法能更优地从多信号源混叠的原始振动信号中识别微弱故障特征所在的最优解调频段；CHMR 相较传统的循环分量比、二阶循环平稳指标和故障出现率，一方面能够更准确地识别轴承的故障部位，另一方面能够更清晰地区分出轴承的故障程度。

（3）本文所提方法适用于轴承单故障情况，未来将考虑多故障（轴箱轴承、车轮踏面、牵引齿轮等）并发条件下的耦合关系，以提升故障自主识别方法在多故障条件下的鲁棒性和稳定性。此外，所提方法在轴箱轴承的早期典型故障诊断方面取得了显著效果，未来将针对轴承后期非典型故障特征下的故障特征量化问题进一步研究，以拓展本算法的工程适用范围。