基于同伦稀疏STAP的低空风切变风速估计
李 海, 程伟杰, 谢瑞杰
(中国民航大学天津市智能信号与图像处理重点实验室, 天津 300300)
0 引 言
低空风切变是一种高度在600 m以下、气流在一个较小的距离内突然改变其方向或速度的大气现象,它具有持续时间短、作用区域小、瞬间强度大、危害性强等特点。当飞机在起降阶段突遇低空风切变时,飞行员往往缺乏充足的时间和空间对飞机姿态进行控制,从而导致飞行事故的发生,因此低空风切变检测和预警成为当前民航领域的一项重要课题,而低空风切变风速估计决定了低空风切变检测的准确程度,因而准确估计低空风切变风速显得至关重要[1]。机载气象雷达能够对航路上的危险气象进行实时探测并发出预警,已经成为保障民航飞机飞行安全必备的航空电子设备。但其属于下视工作模式,所面临的杂波分布范围广、强度大,同时由于飞机运动致使杂波谱严重展宽,从而导致风切变这类分布式气象目标常被淹没于强地杂波之中,故地杂波抑制效果将直接影响风速估计结果[2]。
在机载相控阵雷达系统中,空时自适应处理(space-time adaptive processing, STAP)技术能够在空时联合域有效抑制杂波并达到目标检测的目的。STAP技术的最优权矢量依赖于杂波协方差矩阵(clutter covariance matrix, CCM)的准确估计[3]。但是传统STAP技术要求在独立同分布(independent identically distributed, IID)环境下,IID训练样本达到系统自由度(degree of freedom, DOF)2倍或以上时,方可保证输出信噪比的损失不超过3 dB[4]。然而在实际情况中,传统STAP对于IID训练样本往往难以达到要求,从而无法得到准确的杂波协方差矩阵,此时STAP在实际环境中的性能急剧下降。尤其是在机载前视阵下,地杂波空时二维谱随距离变化呈现差异性,这种杂波特性大大减少了可用于估计杂波协方差矩阵的IID训练样本数量,加大了实现STAP的难度。因此,探讨在少量邻近距离单元的情况下进行低空风切变风速估计具有意义。
目前,在小样本的情况下实现分布式目标参数估计的手段主要有降秩STAP[5]、降维STAP[6]、稀疏STAP[7]等。文献[5]提出了对角加载样本协方差矩阵求逆(loaded sampling covariance matrix inversion, LSMI)方法,该方法直接利用雷达回波数据估计滤波器权向量,能将IID训练样本数目减少至杂波空间维数的两倍多,但是仍需利用较多的IID训练样本估计杂波协方差矩阵,实际应用中难以得到满足;文献[6]提出了基于多通道联合自适应处理(multiple Doppler channels joint adaptive processing, M-CAP)的低空风切变风速估计方法,该方法采用了降维结构,将全局系统自由度降至局域系统自由度,但IID训练样本数量仍然较大。稀疏恢复理论可利用极少观测样本高精度恢复信号[8-9],将该特点与STAP技术相结合可提高在小样本条件下杂波抑制与目标检测性能。然而传统的稀疏恢复方法,如正交匹配追踪(orthogonal matching pursuit,OMP)算法[10]、加权二范数最小化(focal underdetermined system solver,FOCUSS)算法[11]等存在参数设置的问题,其中最重要的参数就是正则化参数和稀疏度。如果稀疏恢复算法对参数比较敏感,则参数设置会影响到其算法的性能。正则化参数是L1范数最优化的问题,在实际中难以设计,而稀疏度尽管在正侧阵下与杂波秩有关,但是风切变检测是处于机载前视阵情况下,此种情况下稀疏度理论研究暂时没有文献报道。因此,研究参数设置简单的稀疏STAP算法,并将其应用至低空风切变风速估计问题中具有重要意义。
针对上述小样本、稀疏恢复算法参数设置难的问题,提出了一种基于同伦稀疏STAP的低空风切变风速估计方法。同伦是一种参数设置简单的非参数化稀疏恢复方法,该方法仅需要少量邻近距离单元就能够获得较为精确的杂波协方差矩阵,然后构建STAP处理器实现对杂波的抑制和归一化多普勒频率估计,最终得到风场速度的准确估计。该方法能够很好地提高小样本条件下杂波协方差矩阵的估计性能,从而有效抑制杂波并对风速进行准确估计。
1 回波信号模型描述
本文中,xl表示第l个待检测距离单元的NK×1维空时二维快拍数据,其表达式为
xl=sl+cl+nl
(1)
式中:sl为第l个待检测距离单元内低空风切变风场产生的雷达回波信号;cl为第l个待检测距离单元内的地杂波,在此假设地杂波没有起伏也不存在模糊现象[12];nl为加性高斯白噪声。
1.1 低空风切变信号模型
第l个待检测距离单元内的低空风切变风场回波信号数据sl为
(2)
(3)
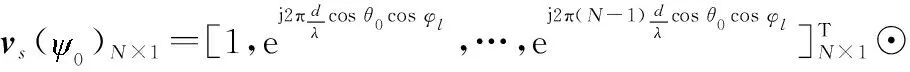
(4)
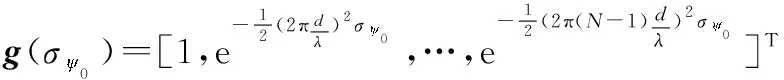
1.2 地杂波信号模型
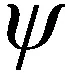
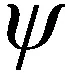
(5)
(6)
式中:α为载机飞行方向与天线阵面之间的夹角,大小为90°。
则第l个待检测距离单元的地杂波回波信号数据cl为

(7)
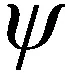
(8)
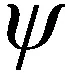
2 基于同伦稀疏STAP的风速估计方法
基于同伦稀疏STAP的风速估计方法首先将少量邻近距离单元进行距离依赖性矫正得到IID训练样本,然后利用同伦算法进行杂波协方差矩阵估计,接着通过构造STAP处理器求解最优权矢量,最后实现杂波抑制和低空风切变风速估计。其中距离依赖性矫正、基于同伦算法的杂波协方差矩阵估计和低空风切变风速估计是同伦稀疏STAP方法的关键步骤,下面分别进行论述。
2.1 距离依赖性矫正
由于机载前视阵下杂波分布具有距离依赖性,从而导致邻近距离单元的杂波空时二维分布特性与待检测距离单元存在差异,因此需要先进行距离依赖性矫正。本文采用多普勒频移(Doppler warping,DW)法进行距离依赖性矫正,该方法简单并且易于工程实现[14]。该方法依据杂波空时二维谱的空间角频率和多普勒频率之间具有耦合特性计算得到各邻近距离单元杂波的多普勒频率,然后将邻近距离单元杂波进行一维多普勒频率平移,使得邻近距离单元与待检测距离单元杂波主瓣重合,从而减少IID训练样本间的杂波空时二维分布的差异性,即降低杂波距离依赖性。
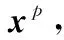
(9)
式中:
(10)
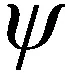
则经过DW矫正后的第p个邻近距离单元为
(11)
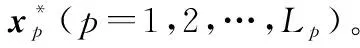
2.2 基于同伦算法的杂波协方差矩阵估计
杂波协方差矩阵估计需要超完备基矩阵和空时分布向量,利用同伦算法恢复在超完备基矩阵下的空时分布向量,就能够获得高性能的杂波协方差矩阵估计。
(1) 超完备基矩阵
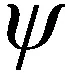
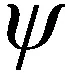
(12)
(2) 空时分布向量
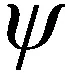
(13)
由于式(13)是一个欠定方程,即存在无数可能的解[15-16]。因此式(13)可以被转化为凸优化中的L1范数最优化问题[17],也称为LASSO(least absolute shrinkage and selection operator)问题来进行求解:
(14)
式中:Γ(αp)是目标函数;β是正则化参数。
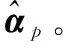
式(14)中的最优化问题可以转化为求目标函数Γ(αp)次微分等于零向量的解,即∂Γ(αp)/∂αp=0[18-19]。目标函数Γ(αp)的次微分表示为
(15)
根据KKT(Karush-Kuhn-Tucker)条件,∂Γ(αp)/∂αp=0可以等价转化[21-22]为
(16)
式中:β≥0;Λ、u分别表示αp的支撑集、αp在其支撑集Λ上的符号序列,支撑集是αp中非零元素所对应单元网格索引的集合;AΛ表示由支撑集Λ对应单元网格的空时导向矢量所组成的集合;Λc表示支撑集Λ的补集,补集是αp中零元素所对应单元网格索引的集合。
同伦算法通过下式进行迭代更新,表达式为
(17)
式中:δ为更新方向;τ为步长。
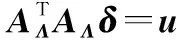
(18)
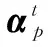
(19)
(20)
(21)
(22)
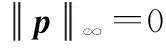
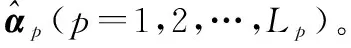
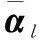
(23)
则其对应的杂波协方差矩阵可表示为
(24)
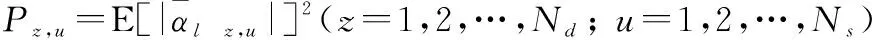
2.3 低空风切变风速估计
根据式(23)得出的杂波协方差矩阵来设计STAP处理器从而消除杂波并估计风速。由线性约束最小方差准则求解最优权矢量,该问题可表示为
(25)
利用最优权矢量wl对雷达回波信号进行处理后,待检测距离单元xl中的地杂波被抑制,且该距离单元低空风切变信号的归一化多普勒频率估计值可由下式搜索得到:
(26)
则第l个待检测距离单元的风场目标速度估计结果为
(27)
3 方法流程
基于同伦稀疏STAP的低空风切变风速估计方法流程如图2所示。
所提方法可以有效地抑制地杂波并进行低空风切变风速估计,其关键步骤如下:
步骤 1利用DW补偿法矫正杂波距离依赖性得到IID训练样本;
步骤 2通过同伦算法计算待检测距离单元的空时分布向量;
步骤 3对待检测距离单元的杂波协方差矩阵进行估计并求解STAP处理器的最优权矢量,接着对地杂波进行抑制;
步骤 4估计待检测距离单元内低空风切变的归一化多普勒频率,从而得出待检测距离单元的风场中心风速估计值。
4 仿真结果及分析
4.1 仿真条件设置
本文中假设低空风切变场中心位于载机平台60°方向距离12.5 km处,天线主瓣对准低空风切变场,低空风切变场宽度为8 km,高度为600 m,风场水平风速范围为-40~40 m/s,垂直风速范围为-20~20 m/s。主要仿真参数如表1所示。
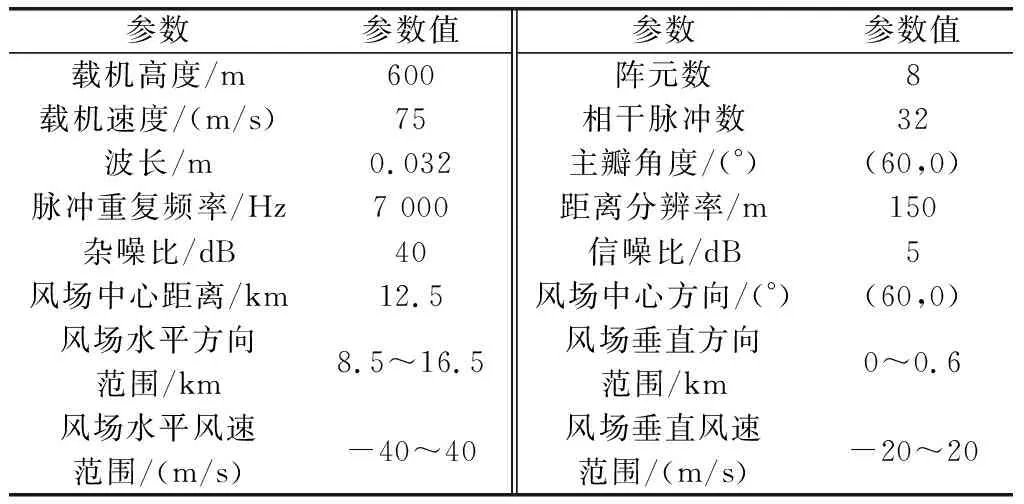
表1 系统仿真参数Table 1 System simulation parameters
4.2 仿真结果分析
图3为机载气象雷达前视阵下雷达回波信号的空时二维谱,由于机载前视阵下地杂波具有空时耦合特性,因此地杂波在空时二维谱中呈现半圆形特征,低空风切变信号功率谱在归一化多普勒频率域和空间锥角余弦域具有一定的展宽。通过分析可得,地杂波的功率比低空风切变信号的功率要强得多,使得地杂波完全掩盖低空风切变信号的归一化多普勒频率信息,这是造成低空风切变估计性能不准确的重要因素。
图4为同伦稀疏STAP算法恢复地杂波空时二维谱,其中图4(a)表示雷达回波信号中的地杂波空时二维谱,图4(b)为直接使用1个IID训练样本得出的空时二维谱,图4(c)~图4(f)为在IID训练样本数量为1、5、10和15时,利用同伦稀疏STAP方法处理得到的空时二维谱。从中可以看出所提方法可以仅使用少量IID训练样本数据就能够高分辨地恢复出地杂波空时二维谱;随着IID训练样本数量的增加,所提方法性能并没有较大改善,说明所提方法对IID训练样本的依赖性比较低。
图5为所提方法、LSMI、M-CAP和OMP方法杂波协方差矩阵的杂波特征谱图。从中可以看出,所提方法和OMP方法同属于稀疏恢复类SATP方法,其杂波协方差矩阵大特征值个数明显要比LSMI和M-CAP两种非稀疏恢复类STAP方法少,即杂波自由度低,更有利于STAP算法性能的提高;同时所提方法的大特征值个数比OMP方法少,说明所提方法得到的杂波协方差矩阵更加准确。图6为所提方法、LSMI、M-CAP和OMP方法在IID训练样本数量为10时的改善因子曲线图,以第60号距离单元为例,从中可以看出所提方法相比于其他3种方法,改善因子曲线在主杂波区凹口更深和更窄,可以更为有效抑制地杂波。
本文方法、LSMI、M-CAP和OMP方法在不同IID训练样本数量时的风速估计结果对比如图7所示。图7(a)为IID样本数为100时风速估计结果,4种方法由于样本数量充足均能够有效估计风速;图7(b)为IID样本数为50时风速估计结果,LSMI方法由于样本数减少无法得到准确的风速估计结果;图7(c)为IID样本数为10时风速估计结果,从中可以看出,所提方法在IID训练样本数量极少时依然可以准确估计风速且精度更高,同时在8.5~16.5 km范围内,风场风速随距离呈现反“S”型变化特征。而LSMI和M-CAP方法由于IID训练样本严重不足导致无法估计风速,OMP方法虽能大致估计风速但存在误差精度较低。
表2为不同样本数的风速估计均方根误差对比。可以看出,随着IID样本数的减少,LSMI、M-CAP和OMP方法的均方根误差变化大,而本文方法的均方根误差变化小,且均方根误差值都小于其他3种对比方法。
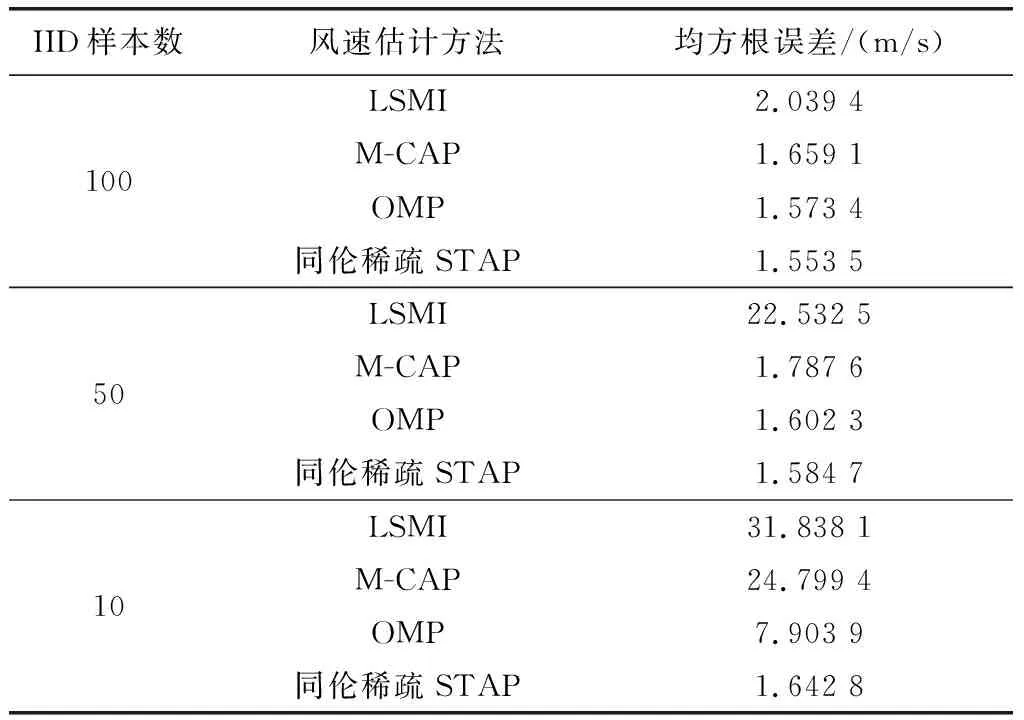
表2 不同样本数的风速估计均方根误差对比Table 2 Comparison of root mean square error of wind speed estimation with different number of samples
图8为IID样本数为100时不同杂波强度下4种方法的风速估计结果对比图。图8(a)~图8(c)为杂噪比分别为40 dB、50 dB和60 dB时的风速估计结果,从中可以看出所提方法在杂噪比增加时依然能够准确估计风速。
表3为不同杂波强度的风速估计均方根误差对比。从表中可以看出,杂噪比的增加对LSMI、M-CAP和OMP方法的均方根误差值影响大,而本文方法的均方根误差值受杂噪比影响较小。
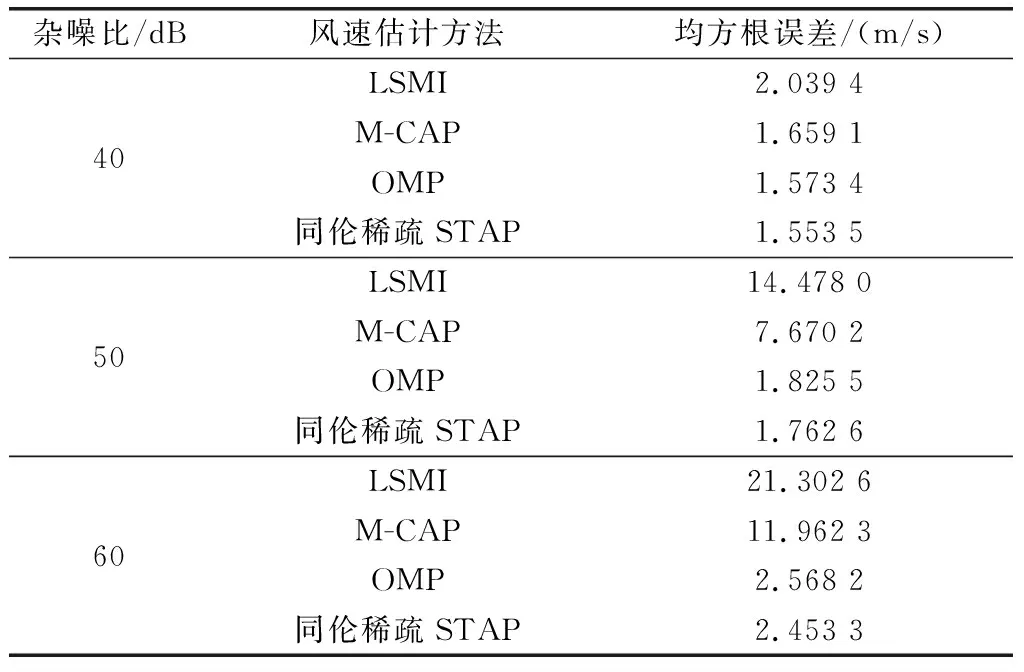
表3 不同杂波强度的风速估计均方根误差对比Table 3 Comparison of root mean square error of wind speed estimation with different clutter intensities
5 结 论
本文将同伦稀疏恢复算法应用到机载气象雷达STAP处理中,并针对在机载气象雷达前视阵下由于IID训练样本不足而导致STAP性能下降的问题,提出了一种基于同伦稀疏STAP的低空风切变风速估计的方法。该方法将待检测距离单元周围的少量邻近距离单元经过距离依赖性矫正后作为IID训练样本,然后对其进行同伦稀疏恢复处理得到高分辨率杂波空时二维谱,进而计算相应的杂波协方差矩阵,通过构造STAP处理器对杂波进行抑制并对低空风切变风速进行估计。仿真结果表明,本文所提方法在IID训练样本数量极少情况下依然可以准确估计风速,可显著降低对IID训练样本的需求。

