丘陵山地作物移栽机井窖式成穴机构设计与试验

徐高伟 荐世春 宋裕民 方会敏 邱绪云 明向兰

(1.山东交通学院汽车工程学院， 济南 250357； 2.山东省农业机械科学研究院， 济南 250100；3.江苏大学农业工程学院， 镇江 212013； 4.岭南师范学院机电工程学院， 湛江 524048)

0 引言

井窖成穴移栽技术是将丘陵山地种植的部分作物小苗，如烟草[1]、辣椒[2]等，移栽到井窖内部。井窖是具有一定深度和高度以及直径一致的穴体，根据达西定律，井窖内随着外界温湿度变化而产生水力递度，迫使井窖内土壤水分蒸发或凝结，从而保持井窖内温湿度的相对稳定[3]。因此通过利用井窖内湿度、温度相对稳定的特点，将作物种苗移栽到井窖穴体后立即浇水、施药并覆盖地膜，能实现丘陵山地作物移栽的壮苗培育、适时早栽和高垄深栽，从而增加其抗旱能力、减轻病虫害，以达到丘陵山地作物提质增效的一种栽培方式[4]。目前已在山东省临沂、淄博等丘陵山地进行部分推广[5-6]。

目前丘陵山地移栽装备主要是以传统栽植农艺为基础的鸭嘴式移栽机为主[7-13]，无法形成稳定的井窖，穴体易坍塌，不能适应丘陵山地作物井窖式移栽的农艺要求。用于丘陵山地移栽机的井窖式成穴装置，目前有3种型式：人力背负式井窖成穴装置[14]，由汽油机驱动，人工控制穴体位置和深度，成穴效率较低、劳动强度较大；多连杆式成穴机构[15-16]，该机构在成穴过程中，由于与移栽机前进速度无法完全匹配，所成穴体形状为“喇叭形”，无法满足井窖成穴的农艺要求；间歇式井窖成穴装置[17-18]，与间歇运动底盘配套作业，到达指定位置时底盘停止前进，成穴装置沿垂直垄面方向成穴，该装置避免了成穴机构与底盘作业速度的匹配问题，穴体质量较好，但由于底盘的间歇运动，作业效率和机具可靠性不高。

针对以上情况，本文结合井窖成穴移栽技术提出的井窖成穴农艺要求，基于非圆齿轮-平行四杆机构，设计一种用于丘陵山地移栽机的井窖式成穴机构，该机构利用非圆齿轮连杆机构近似匀速直线运动的特性，抵消机构前进作业速度，在机具连续作业下形成适用于丘陵山地作物井窖移栽大深度、高规格的井窖穴体，提高机械化井窖成穴的工作效率和作业质量，降低人工成穴的劳动作业强度。

1 成穴农艺要求分析

井窖成穴农艺要求如图1所示。穴距为500 mm、井窖形状为圆形、穴体深度为180～200 mm、穴体直径为60～80 mm，穴体整体直径应较均匀，内壁坚实不坍塌。

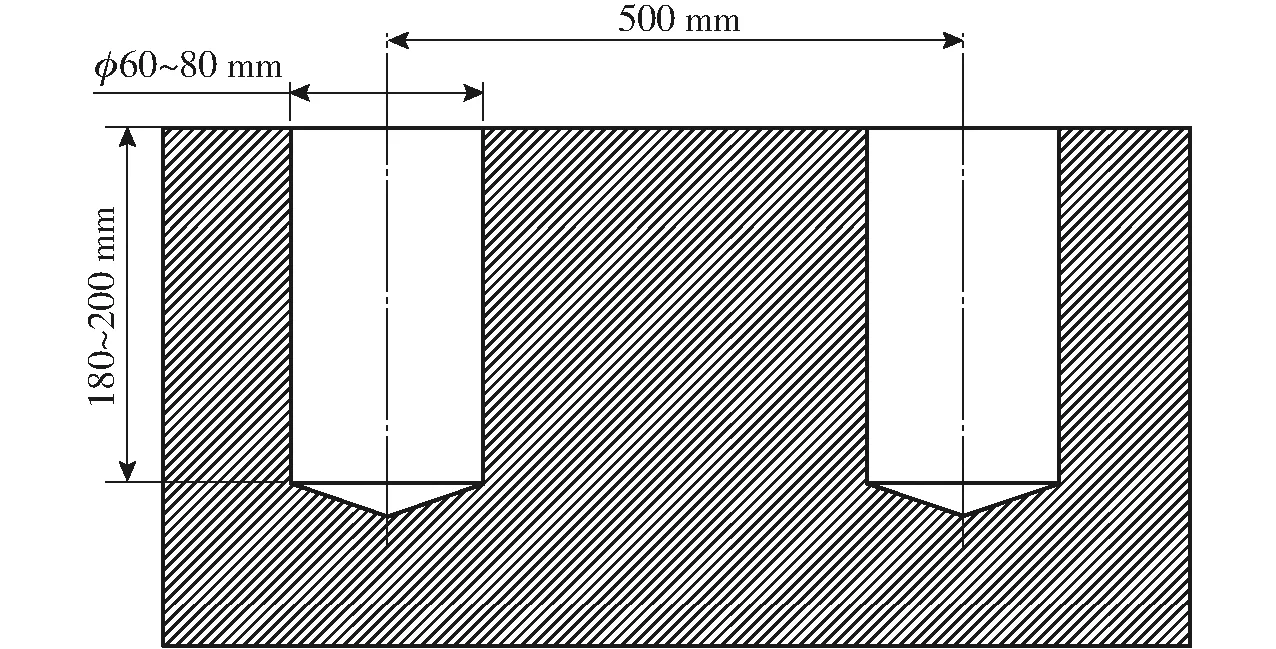
图1 井窖成穴的农艺要求Fig.1 Agronomic requirements for cellar cavitation

机构设计的难点在于：在机具连续作业的情况下，井窖成穴机构所成穴体要在达到较大深度的同时保证井窖穴体的直径以及单个井窖穴体轮廓直径的一致性。

2 成穴机构组成与工作原理

井窖成穴机构结构示意图如图2所示，该机构主要由非圆齿轮-平行四杆机构以及成穴器组成。其中非圆齿轮1、3组成非圆齿轮传动机构；直齿圆柱齿轮2、4、5组成齿轮传动机构，AB、CD、AC、BD为四杆机构的双曲柄、机架和连杆，与直齿圆柱齿轮2、4、5组成平行四杆机构；直齿圆柱齿轮6通过键连接固联在曲柄CD铰接点D处，直齿圆柱齿轮7固联安装在与连杆BD一体的锥齿轮换向减速器的动力输入轴上，与直齿圆柱齿轮6组成齿轮传动机构；成穴器8安装在锥齿轮换向减速器动力输出轴上。

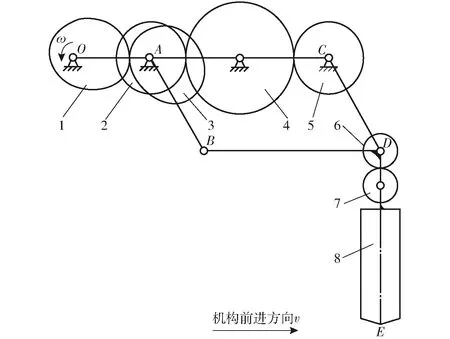
图2 成穴机构示意图Fig.2 Schematic of cavitation mechanism1、3.非圆齿轮 2.左侧圆柱齿轮 4.中间圆柱齿轮 5.右侧圆柱齿轮 6、7.成穴器动力传递圆柱齿轮 8.成穴器

作业时，匀速转动的动力由非圆齿轮1传入，通过非圆齿轮1、3组成的非圆齿轮机构将匀速转动转变为变速转动；直齿圆柱齿轮2与非圆齿轮3同轴心固联，又通过直齿圆柱齿轮2、4、5组成的直齿圆柱齿轮传动机构，将变速转动传递给平行四杆机构的曲柄AB和CD，带动连杆BD做变速的摆动；成穴器8与连杆BD垂直安装，随连杆BD做变速摆动，入土和出土过程中在水平方向上形成与机具前进速度大小相近、方向相反的速度，以抵消机具作业的前进速度，形成直径较均匀的井窖穴体。成穴器8随连杆BD摆动的过程中，曲柄CD的变速转动通过直齿圆柱齿轮6、7组成的齿轮机构以及锥齿轮换向减速器将动力传递至成穴器8，带动成穴器做变速转动，以在成穴过程中压实穴体内壁。

3 成穴机构运动学模型与辅助界面建立

以非圆齿轮1旋转中心点O作为坐标原点，水平方向为x轴，竖直方向为y轴建立如图3所示的平面直角坐标系。

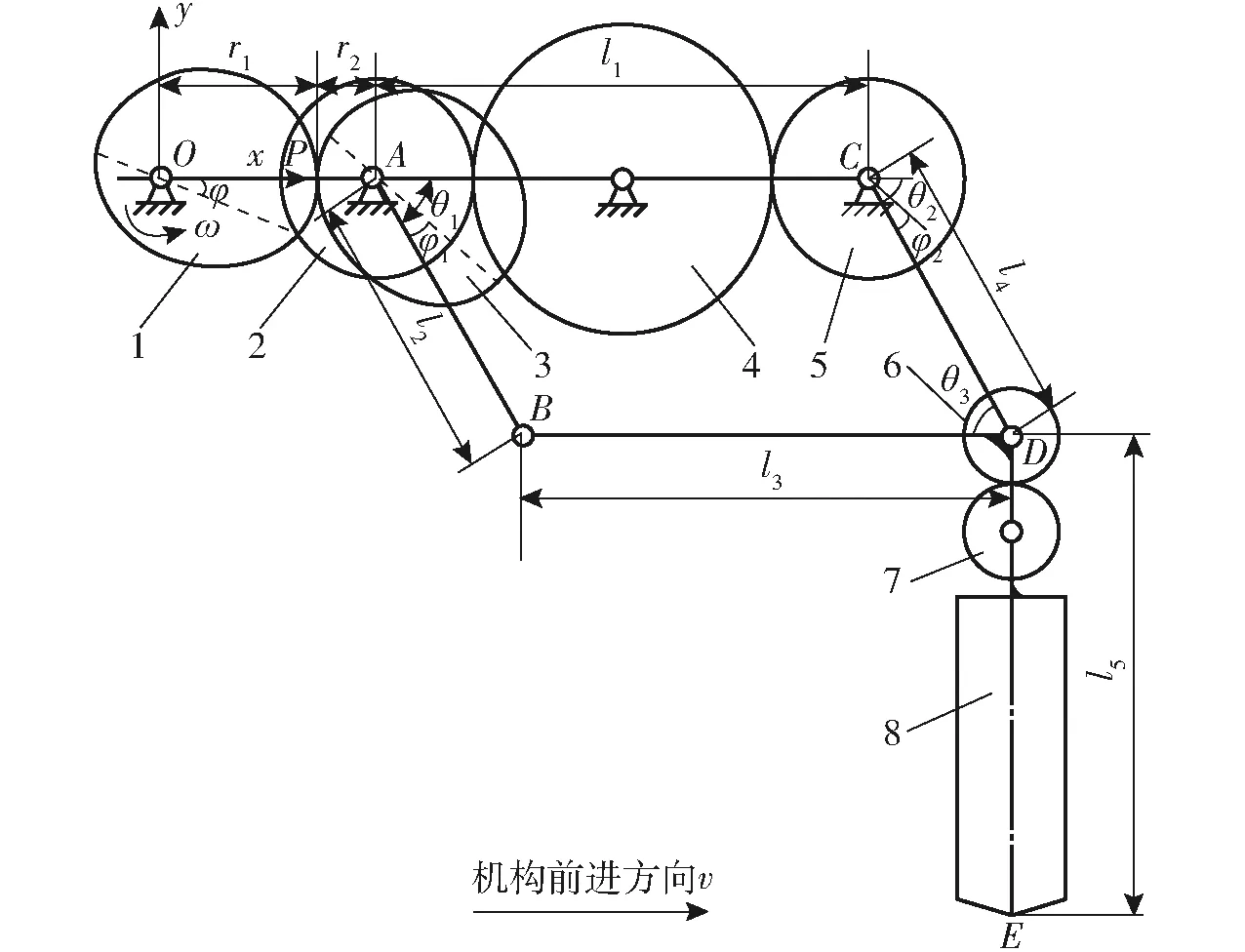
图3 成穴机构运动学模型Fig.3 Kinematic model of cavitation mechanism1、3.非圆齿轮 2.左侧圆柱齿轮 4.中间圆柱齿轮 5.右侧圆柱齿轮 6、7.成穴器动力传递圆柱齿轮 8.成穴器

3.1 位移模型

非圆齿轮3相对于非圆齿轮1的角位移[19-20]为

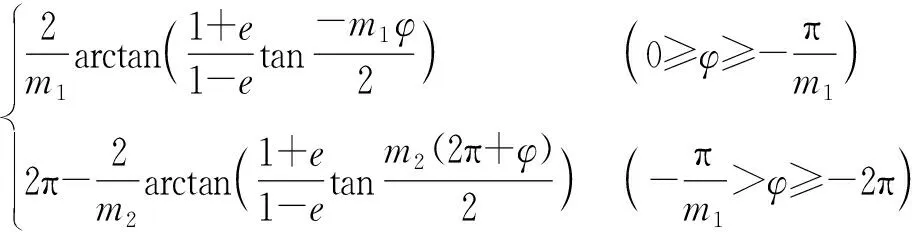
(1)

式中e——非圆齿轮偏心率

m1、m2——非圆齿轮变形系数

φ——非圆齿轮1的角位移，rad

其中，为保证非圆齿轮两段节曲线封闭，m1和m2应满足

(2)

非圆齿轮的节曲线方程为

(3)

r2=2a-r1

(4)

式中r1——非圆齿轮1轴心到啮合点P距离，mm

r2——非圆齿轮3轴心到啮合点P距离，mm

a——非圆齿轮长半轴长度，mm

点A的位移方程为

(5)

式中XO——点O在x方向上的坐标

YO——点O在y方向上的坐标

点B的位移方程为

(6)

式中l2——曲柄AB长度，mm

θ1——曲柄AB初始安装角，rad

点C的位移方程为

(7)

式中l1——平行四杆机构机架AC长度，mm

点D的位移方程为

(8)

式中l4——曲柄CD长度，mm

θ2——曲柄CD初始安装角，rad

φ2——曲柄CD转动的角位移，rad

由平行四杆机构的运动特性可得

(9)

点E的位移方程为

(10)

式中l5——平行四杆机构铰接点D到成穴器下端点的长度，mm

3.2 速度模型

点D的速度方程为

(11)

点E的速度方程为

(12)

其中，由反转法可得

(13)

3.3 辅助界面建立

根据所建立的成穴机构运动学数学模型，基于Matlab GUI模块，开发人机交互可视化辅助界面，如图4所示。

图4 成穴机构人机交互辅助界面Fig.4 Human computer interaction auxiliary interface of cavitation mechanism

4 参数正交仿真试验优化

通过成穴机构人机交互可视化辅助界面，结合仿真试验设计优化方法得到成穴机构优化变量与优化目标的回归方程，以回归方程为基础进行多目标函数优化，获取成穴机构的参数优化组合。

4.1 试验因素与指标确定

结合成穴机构人机交互辅助界面通过单因素预试验，确定运动学方程中平行四杆的曲柄长度l2、非圆齿轮偏心率e、非圆齿轮变形系数m1为影响穴体质量的显著因素，而穴体质量的标准根据成穴农艺分析结果，由穴体深度y1、穴体顶端和底端中点连线与垄面线夹角y2、穴体直径最大值y3、穴体直径最小值y4、穴体最大值与最小值差值y5以及穴体直径方差y6作为评价指标[21-22]。上述指标中用穴体顶端和底端中点连线与垄面线夹角衡量穴体的直立度，穴体直径最大值、穴体直径最小值、穴体直径最大值和最小值的差值、穴体直径的方差衡量穴体直径总体所处的范围和穴体轮廓直径的一致程度。

4.2 试验内容与方法

根据单因素预试验结合试验指标确定成穴机构曲柄长度范围175～195 mm、非圆齿轮偏心率0.35～0.55、非圆齿轮变形系数1.2～1.4，同时确定因素的水平为五水平，在此基础上利用成穴机构人机交互辅助界面，结合二次正交旋转中心组合试验方法，确定成穴机构最佳参数组合。试验因素编码如表1所示，通过辅助界面测定穴体11组直径数据并进行计算获得评价指标。

表1 试验因素编码Tab.1 Experimental factors and codes

4.3 试验结果与分析

试验方案与结果如表2所示，各响应指标的方差分析如表3所示，x1、x2、x3为因素编码值。

表2 试验方案与结果Tab.2 Experimental plan and results

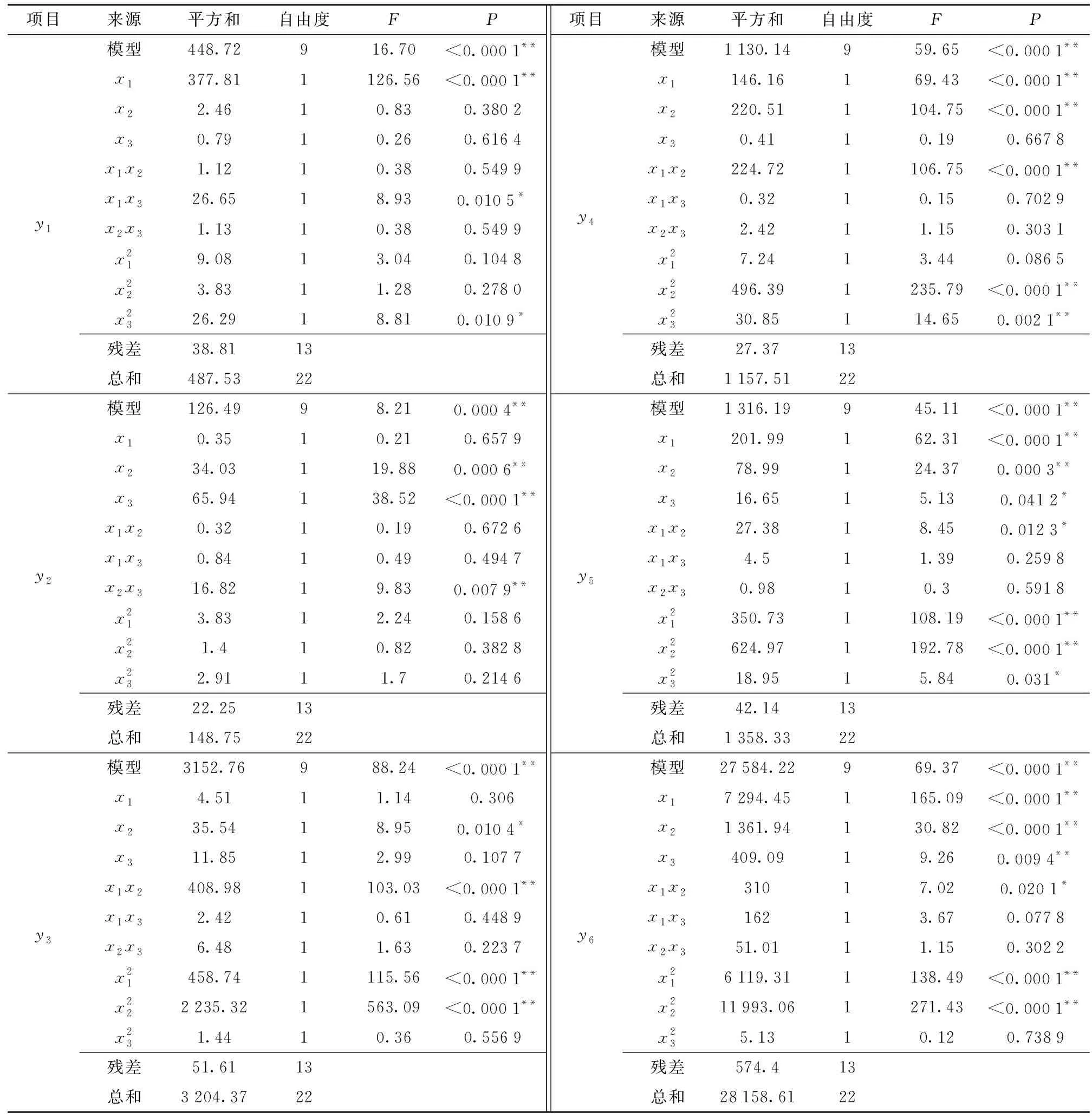
表3 回归模型方差分析Tab.3 Variance analysis of regression model

通过Design-Expert 8.0软件对试验数据进行回归分析和因素方差分析，剔除交互项和二次项中的不显著项，得出指标与因素编码值间的回归方程

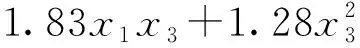
(14)

y2=91.63+0.16x1+1.58x2+2.19x3+
1.45x2x3

(15)

(16)

(17)

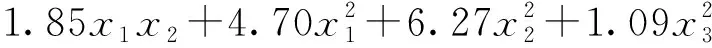
(18)

(19)

为分析各因素对各响应指标的影响规律，运用Design-Expert 8.0软件得到响应曲面，如图5所示。

曲柄长度l2与非圆齿轮变形系数m1在其他因素为零水平时对穴体深度的影响如图5a所示。非圆齿轮变形系数处于零水平以下时，穴体深度随曲柄长度的增加而呈上升趋势；当非圆齿轮变形系数处于零水平以上时，穴体深度随曲柄长度的增加上升趋势明显加大，这是由于曲柄长度越大，成穴器竖直方向上所能达到的位置就越低，穴体深度就越大；而非圆齿轮变形系数会改变成穴器在水平方向上的速度，造成穴体角度的改变，进而改变穴体的垂直深度；非圆齿轮变形系数越大，对垂直度的影响越小，穴体的垂直深度就越大；曲柄长度处于零水平以下时，穴体深度随非圆齿轮变形系数的增加而呈下降趋势，这是由于曲柄长度在零水平以下发生变化时，与非圆齿轮变形系数的交互作用会降低成穴器在水平方向上的速度，使穴体的倾斜度加大，降低穴体垂直深度；当曲柄长度处于零水平以上时，穴体深度随着非圆齿轮变形系数增加，在零水平以下不变，零水平以上呈上升趋势，这是由于曲柄长度在零水平以上发生变化时，与非圆齿轮变形系数的交互作用会不断提高成穴器在水平方向上的速度，逐步逼近机构前进的速度，使穴体的倾斜角度不断减小，增加穴体垂直深度。

非圆齿轮变形系数与非圆齿轮偏心率在其他因素为零水平时对穴体顶部与底部中点连线与垄面线夹角影响如图5b所示。非圆齿轮变形系数处于零水平以下时，穴体顶部与底部中点连线与垄面线夹角随曲柄非圆齿轮偏心率的增加而呈上升趋势；当非圆齿轮变形系数处于零水平以上时，穴体顶部与底部中点连线与垄面线夹角度随曲柄非圆齿轮偏心率的增加上升趋势明显加大；非圆齿轮偏心率处于零水平以下时，穴体顶部与底部中点连线与垄面线夹角随非圆齿轮变形系数的增加而呈上升趋势；当非圆齿轮偏心率处于零水平以上时，穴体顶部与底部中点连线与垄面线夹角随非圆齿轮变形系数的增加上升趋势明显加大。这是由于非圆齿轮变形系数和非圆齿轮偏心率的增加不断改变成穴器在水平方向上的速度，导致穴体顶部与底部中点连线与垄面线夹角不断增加。

曲柄长度与非圆齿轮偏心率在其他因素为零水平时对穴体直径最大值和最小值的影响如图5c、5d所示。当非圆齿轮偏心率处于零水平以上时，穴体直径最大值和最小值均随曲柄长度的增加而呈下降趋势；非圆齿轮系数处于零水平以下时，穴体直径最大值和最小值随曲柄长度的增加而呈上升趋势，这是由于曲柄长度越大在水平方向上的速度越大，与机构前进方向速度的差值越大，所形成的穴体直径也越大，而非圆齿轮偏心率在零水平以下时，对曲柄长度在水平方向的速度影响越小，穴体直径呈上升趋势；而随着非圆齿轮偏心率不断增大(零水平以上)，对曲柄长度在水平方向的速度影响不断增大，降低曲柄长度在水平方向的速度，穴体直径呈下降趋势；当非圆齿轮偏心率处于零水平以上时，穴体直径最大值和最小值随曲柄长度的增加而呈下降趋势；非圆齿轮系数处于零水平以下时，穴体直径最大值和最小值随曲柄长度的增加而呈上升趋势，这是由于曲柄长度越长在水平方向上的速度越大，与机构前进方向速度的差值越大，所形成的穴体直径也越大，而非圆齿轮偏心率较小(零水平以下)时，对成穴机构在水平方向的速度影响越小，穴体直径呈上升趋势；而随着非圆齿轮偏心率不断增大(零水平以上)，对成穴机构在水平方向的速度影响不断增大，降低成穴机构在水平方向的速度，穴体直径呈下降趋势。

曲柄长度与非圆齿轮偏心率在其他因素为零水平时对穴体直径最大值和最小值差值的影响如图5e所示。当非圆齿轮偏心率一定时，穴体直径最大值和最小值的差值随曲柄长度的增加而呈先降低后上升趋势；非圆齿轮偏心率处于零水平以下时，穴体直径最大值和最小值的差值随曲柄长度的增加而呈上升趋势，这说明曲柄长度与非圆齿轮偏心率在零水平附近时，成穴机构在水平方向上的速度接近于机构前进速度，穴体直径最大值和最小值的差值最小。

曲柄长度与非圆齿轮偏心率在其他因素为零水平时对穴体直径方差的影响如图5f所示。曲柄长度一定时，穴体直径的方差随非圆齿轮偏心率的增加先降低后上升；当非圆齿轮偏心率一定时，穴体直径的方差随曲柄长度的增加先降低后上升，这说明随着曲柄长度与非圆齿轮偏心率两因素水平的变化，成穴器在水平方向上的速度存在波动，引起穴体的各部分直径发生较大变化，而导致穴体直径方差较大。当成穴器所在水平方向上的速度接近于机构的前进速度时，穴体各部分直径变化程度越小，穴体直径的方差就越小。

图5 各因素对试验指标影响的响应曲面Fig.5 Response surfaces of factor to test index

4.4 参数优化

为得到试验因素最佳水平组合，对试验因素进行优化设计，建立参数优化的数学模型。结合试验因素的边界条件，对成穴机构响应指标的回归方程进行分析，得到其非线性规划的优化模型

(20)

运用Design-Expert 8.0软件优化模块对回归方程进行多目标参数优化，当曲柄AB和CD长度为184.710 mm、非圆齿轮偏心率e为0.447、非圆齿轮变形系数m1为1.278时，所成穴体各参数为最优，穴体深度为182.3 mm、穴体顶端中点与穴体底端中点连线与垄面线夹角为89.8°、穴体直径最大值为72.8 mm、穴体直径最小值为63.6 mm、穴体直径最大值与最小值差值为10.7 mm、穴体直径方差为6.32 mm2，所成穴体如图6所示。

图6 辅助界面输出的穴体截面Fig.6 Cavity section outputed by auxiliary interface

通过辅助界面输出优化参数下的成穴机构端点在水平方向上分速度曲线，如图7所示。图中，椭圆区域为成穴机构在成穴时成穴器的速度状态，此时成穴器在水平方向上的速度接近于0，说明成穴过程中成穴器在水平方向上的速度与机具的前进速度几乎抵消，满足成穴机构在速度上的设计要求。

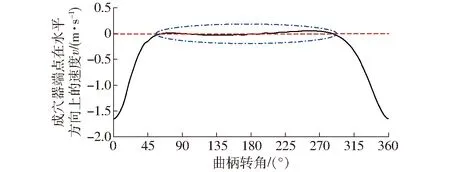
图7 优化参数下成穴机构端点在水平方向上速度曲线Fig.7 Horizontal velocity curve of end point of mechanism with optimized parameters

将上述参数优化组合分别通过回归方程和辅助界面得到各指标值如表4所示。由表4可知，与辅助界面相比，通过回归方程得到各响应指标参数值的误差在合理范围内，验证了回归方程和参数优化的准确性。

表4 回归方程与辅助界面输出的指标值Tab.4 Output index value of regression equation and auxiliary interface

5 试验

5.1 机构设计与制造

根据优化参数对成穴机构进行结构设计，如图8所示。该机构由非圆齿轮机构、直齿齿轮机构、平行四杆机构、锥齿轮换向器以及成穴器组成。实物图如图9所示。

图8 成穴机构三维模型Fig.8 Three-dimensional model of cavitation mechanism1.平行四杆机构 2.直齿圆柱齿轮机构 3.成穴器 4.传动链 5.机架 6.锥齿轮换向器 7.直齿齿轮轮系 8.非圆齿轮机构

5.2 田间试验

5.2.1试验条件

为验证井窖式成穴机构的作业性能，研制了搭载成穴机构的自走式作业平台。试验条件为丘陵山地作物种植常规的大垄，大垄规格为：垄面宽为0.4 m，垄高为0.3 m，垄距为1.2 m。根据上述作业条件对成穴机构进行重复性田间试验，试验在山东省农业机械科学研究院试验基地进行，如图9所示。

图9 田间成穴试验Fig.9 Field cavitation tests

5.2.2试验方法与设备

试验测定所成穴体的穴体深度、与仿真测定位置相同的11组穴体直径数据、穴距以及穴体直立角度等参数。测量时使用铁锹沿穴体的中心位置挖开，获取穴体的截面，如图10所示。使用卷尺和角尺进行上述参数测量，随机测量5组不同穴体的参数，并计算其平均值[23-25]。

图10 实际形成的穴体截面Fig.10 Actually formed cavity section

试验设备包括：187-101型数显角尺(量程：0°～360°)、卷尺(量程：1～3 m)、标杆和计时器等。

5.2.3试验结果

穴体测量数据如表5所示。测定5组穴体各参数的平均值在设计要求范围内，与仿真值相比较存在误差，误差最大值7.6%，最小值为1.8%，产生误差的原因是试验田地形起伏以及机构振动；而测量的5组穴体中，各组穴体的参数也具有差异性，究其原因是作业平台前进速度发生波动，导致成穴机构成穴器在前进方向上的速度与作业平台前进速度的差值也产生波动，造成各组穴体参数的差异。

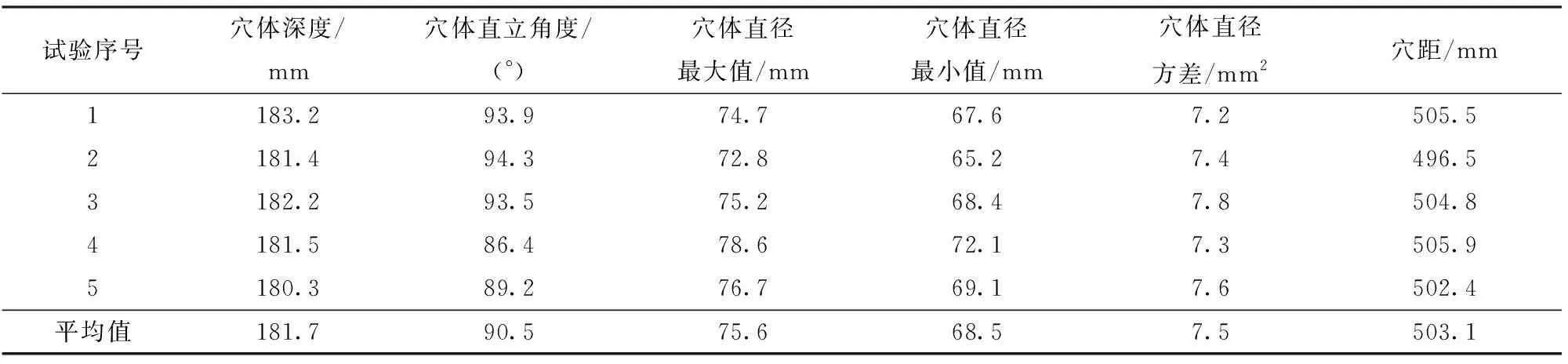
表5 穴体测量数据Tab.5 Measurement data of cavitation

6 结论

(1)根据井窖成穴的农艺要求，基于非圆齿轮-平行四杆设计一种井窖成穴机构，建立了机构运动学模型，结合机构运动学模型采用Matlab开发了人机交互可视化辅助界面。

(2)借助辅助界面结合二次正交旋转中心组合试验方法，通过Design-Expert 8.0软件建立成穴机构响应指标与试验因素的回归方程，通过响应曲面得出成穴机构试验因素对响应指标的影响趋势和交互关系；以回归方程为基础，采用多目标函数优化得到成穴机构优化参数组合：曲柄长度l2为184.710 mm、非圆齿轮偏心率e为0.447、变形系数m1为1.278。

(3)根据优化后的参数研制成穴机构样机及田间作业平台并进行田间试验，试验结果表明：穴体深度为181.7 mm、穴体直立角度为90.5°、穴体直径最大值为75.6 mm、穴体直径最小值为68.5 mm、穴体直径方差为7.5 mm2、穴距为503.1 mm，优化后的成穴机构满足井窖成穴的农艺要求。