根系水分胁迫响应函数对土壤水及作物生长动态和产量模拟影响的研究

王铁英， 王仰仁， 柴俊芳， 郭文俊

（1.天津农学院水利工程学院，天津 300392；2.山西省洪洞县霍泉水利事务中心灌溉试验站，山西 临汾 031600）

根系水分胁迫响应函数被定义为实际根系吸水速率与最大根系吸水速率之比，是研究干旱胁迫对根系吸水影响的重要参数。根系吸水是植物获取水分、养分、进行光合作用的基础，也是联系水循环和碳循环的纽带［1］。在土壤水分动态及产量的模拟中，根系吸水模型是极为重要的组成部分［2］，模拟效果直接影响土壤水分动态模拟及产量模拟精度［3］。宏观条件［4-5］下的经验模型［6］常用于模拟根系吸水过程，模型主要考虑根系吸水同根系密度分布、土壤剖面含水率、蒸腾速率的关系［7-8］。作物的根系吸水速率往往难于直接测试，因此康绍忠等［2］直接分析了土壤剖面充分湿润时的根系吸水速率随深度的变化规律，并依据土壤-植物的水平衡关系得出了土壤剖面均匀湿润时的根系吸水速率模型，用于计算最大根系吸水速率，在实际应用中较为简单。

土壤剖面含水率对根系吸水有直接影响，当土壤含水率降低时，根系吸水受到抑制，吸水速率小于充分湿润时的吸水速率［2］。根系水分胁迫响应函数用于反映土壤水分胁迫对根系吸水的抑制作用，使根系吸水模型可以适用于干旱、半干旱条件，朱永华等［8］引入土壤湿度有关的参数改进了根系吸水模型，得出了干旱荒漠区域的根系吸水模型。根系水分胁迫响应函数主要表征为土壤含水率或土壤基质势的分段函数，有线性［9-10］和非线性［11］两类。

线性函数表明根系吸水速率随土壤基质势或土壤含水率的下降呈线性减小趋势，其中Feddes等［12］所提出的分段线性函数最为典型。非线性函数分为S型函数［13］和凹凸型函数［14-15］2种，二者均表明根系吸水速率随着土壤基质势或土壤含水率变化是一个渐变的过程，其中分别以Van Genuchten模型［16］和康绍忠等［2］建立的适用于小麦根系吸水模式的指数模型较为简便、典型。与线性函数相比，非线性的土壤水分胁迫响应函数在大多数情况下能更加准确地表征土壤水分对根系吸水的影响［17］。凹凸型响应函数在分段连接处会出现变化速率突变，为避免该现象本研究提出了以土壤含水率为变量的S型水分胁迫响应函数模型，与另外2 种典型的根系水分胁迫响应函数进行对比分析，该对比在作物水模拟过程中完成。

作物水模型主要用于对作物生长发育动态、产量进行模拟，是定量化评价灌水施肥等田间管理措施的重要手段［18］，其模拟对象主要为土壤水、土壤氮素和作物生长。土壤水的模拟主要是土壤水分运动与蒸散过程，不同的模型采用方法不同，如在水分模拟中，WOFOST［19］、DSSAT［20］、PS123［21-22］等模型采用计算较为简单的水平衡法，而HYDRUS-1D［23-24］、DAISY［25］等模型则采用了以Richards［7］方程为基础的土壤水动力学模型，更适用于边界条件复杂的环境且计算精度较高［26］。作物蒸散模拟中大部分模型采用了Penman-Monteith 方程计算参考作物蒸散量，通过作物系数计算潜在蒸散量，最后使用叶面积指数将潜在蒸散量分为潜在蒸腾量和潜在蒸发量，实际蒸发量可作为Richards方程的上边界条件，潜在蒸腾量输入作物根系吸水模型作为实际根系吸水的驱动。作物生长模拟过程是从光合有效辐射出发，考虑光、温、水和养分等胁迫，描述光合作用及干物质积累、分配和转化过程。目前，既有较通用的WOFOST、DSSAT、DAISY 等模型，也有针对不同作物的特定模型，如用于模拟谷类作物的CERES［27］模型。以荷兰De Wit 教授为首的研究小组，先后建立和完善了在不同生产力水平下的作物生长模拟模型，以PS123模型为代表，更多地强调作物的共性，与作物的生理生态机理结合较紧，在我国的适应性方面已有良好的工作基础［28］，如毛振强等［29］以河北曲周县30 a 的气象数据为依据，应用PS123模型分析了该地区夏玉米的需水量和优化灌溉方案，对指导当地玉米生产具有重要意义。

PS123模型是联系水分与作物生长关系的主要环节，其对于水分动态模拟采用简化的水平衡法，对根系吸水只是依据机理进行了较为简单的线性化处理，需要进一步完善［30］。鉴于此，本研究选用PS123 作物生长模型与Richards 方程建立了作物产量与水分关系，并采用机理性较强的根系吸水模型。采用规划求解方法对模型参数进行率定，对不同形式水分胁迫响应函数的表征效果进行了评价。

1 研究区概况

1.1 试验站概况

以冬小麦作为研究对象，以山西霍泉、潇河两处试验站的试验资料为依据。霍泉站位于霍泉灌区中上游的洪洞县广胜寺镇东安村（111°46′21″E，36°17′35″N），海拔高程529 m，该地所属气候为暖温带大陆性气候，土壤质地为轻壤土，0～100 cm 土壤容重1.46 g·cm-3，田间持水率为0.3592 cm3·cm-3。潇河试验站位于晋中市榆次区杨村（112°41′31″E，37°39′06″N），海拔高程782.64 m，土质为重壤土，0～100 cm 土壤容重为1.42 g·cm-3，田间持水率为0.4044 cm3·cm-3。

模拟中取用了霍泉站2017—2019 年与潇河站2004—2005 年共5 个站年的冬小麦试验资料（小麦生育期跨越冬季，本文中年为收获年），主要包括各年的气象数据、冬小麦生长发育期的干物质测试数据及土壤含水率实测数据。其中，土壤含水率测试方法，霍泉站为烘干法，潇河站为中子仪法。霍泉站为大田试验，小区面积为66.7 m2，潇河站采用了无底测坑，测坑面积为3.33 m×2 m。

1.2 试验处理选定

霍泉站与潇河站均为冬小麦水肥耦合试验。其中，霍泉站每年设置6个处理，潇河站每年设置10个处理。本研究仅在每年的试验处理中选取了高水、中水和零水处理用于模型参数的率定，详细处理信息见表1。由表可见，不同年份、处理间施肥数量有所不同，因此研究中土壤含水率、蒸散量和产量的变化为水肥双重影响下的结果。

表1 冬小麦水肥耦合试验处理基本信息Tab.1 Basic information of winter wheat water and fertilizer coupling test treatment

2 研究方法

2.1 土壤水热耦合变化动态模拟

2.1.1土壤水热耦合动态模拟模型 本研究在冬小麦生育期水分模拟的过程中考虑了温度变化，采用包含根系吸水项的Richards方程进行土壤水分动态模拟，以1 d 作为模拟时段，对距地表2 m 内的土壤含水率及热流进行分层模拟（20 cm 一层），依据STVF 理论模式［31］分析土壤温度变化对土壤水分运动特性参数的影响。采用尚松浩等［16］给出的水热耦合方程模拟热流变化，该方程综合考虑了土壤水分迁移、热传导、水分相变等因素，相对于传统水热耦合方程，水、热方程间的耦合性大为减少，可以不考虑相变作用，只在计算时段末根据冻结曲线进行冰和未冻水含量的修正，有利于提高方程求解的迭代计算。

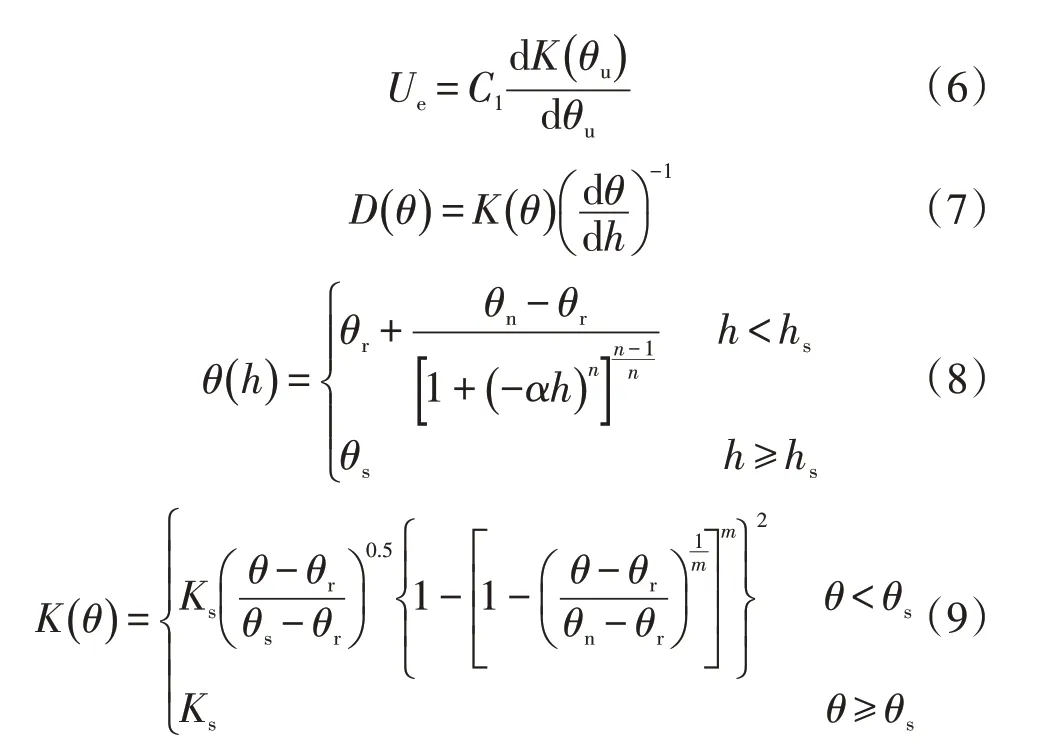
上述水热耦合方程与初始条件、边界条件一起组成完整的水热耦合动态模拟模型。初始条件、边界条件采用王仰仁［33］论文中给出的计算方法，初始条件中土壤含水率为播种日土壤剖面含水率，气温根据自动气象站测得，地温采用地温温度计测得；上边界条件中地表通量等于棵间土壤蒸发量［33］，地表温度根据空气温度与地表温度的经验关系计算；下边界条件中的温度及土壤含水率因在小麦生育期内变化较小，因而采用第一类边界条件［34］。利用差分方法求解，可得分层土壤含水率及温度随时间的变化过程。

2.1.2根系吸水模型 采用潜在的根系吸水速率与水分胁迫响应的乘积计算根系的实际吸水速率［2］。

式中：S(z,t)为根系吸水速率（min-1）；S0(z,t)为土壤充分湿润条件下的根系吸水速率（min-1），采用Novák［35］给出公式计算，见式（11）；β为水分胁迫响应函数，是以土壤基质势或土壤含水率为自变量的函数。

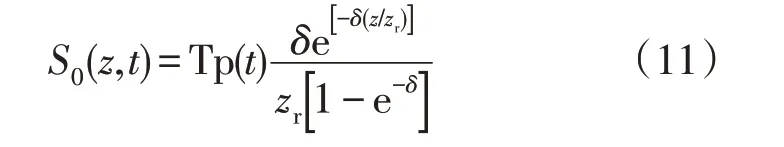
式中：Tp(t)为作物潜在蒸腾速率（cm·min-1），是作物潜在蒸散量的一部分，可根据经验公式计算得到［33］；z为深度（cm）；zr为根系层深度（cm）；δ为经验系数，与作物种类有关，本文参照由懋正［31］的研究取δ=3.8。

本研究对3种形式的水分胁迫响应函数进行了对比分析。

（1）以土壤基质势为因变量的Van Genuchten函数［14］（以下称为VG）。

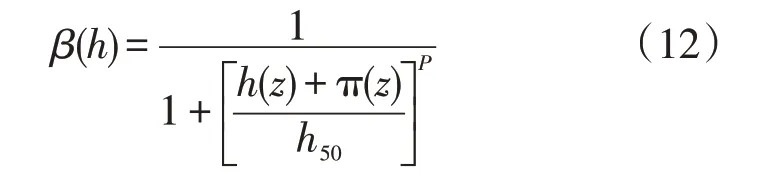
式中：β(h)为以土壤基质势为自变量的水分胁迫响应函数，呈S形状变化；h(z)为地面以下深度z处的土壤基质势（cm）；π(z)为土壤溶质势，本研究未考虑溶质影响，因此取π(z)=0；P为经验系数，通过参数反演确定；h50为作物蒸腾量减小到最大可能蒸腾量50%时所对应的土壤水势（cm），其值通过参数反演确定。

（2）以土壤含水率为因变量的幂函数［14］（以下称为MP）。

式中：β(θ)为以土壤含水率为自变量的水分胁迫响应函数，呈凹（凸）形状变化；AW为有效土壤含水率的相对值；θz为z深度的土壤含水率（cm·cm-3）；θj为临界土壤含水率（cm·cm-3）；θwp为凋萎土壤含水率（cm·cm-3）；A为经验系数；θj、θwp和A通过参数反演确定。

（3）以土壤含水率为因变量的改进型分段函数，式（13）在分段连接点处会出现速率突变，不符合作物生长的连续渐变过程，鉴于此引入参数B、C消除速率突变，形成S型曲线，由此给出了LS，计算公式如下：

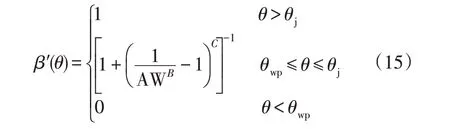
式中：β′(θ)为改进线型的水分胁迫响应函数；B、C为经验系数，通过参数反演确定。

2.2 冬小麦产量模拟

采用PS123 作物生长模型进行冬小麦产量模拟，模拟过程中除了考虑有效太阳辐射和温度外，同时考虑有效水分和有效养分胁迫的影响。模拟产量利用大田作物总的同化潜力表示［36］，计算过程如下：

式中：Fgassi为大田作物总同化率（kg·hm-2·d-1）；Fgci为密闭参照作物总CO2吸收率（kg·hm-2·d-1），根据日长、温度、叶面积指数、消光系数、光能利用效率、冠层顶部截获的光合有效辐射计算［30］；30/44 为CH2O与CO2的分子量之比；FWi为水分胁迫系数；FNi为养分胁迫系数，分别采用式（17）［37］和式（18）计算；CVF为光合产物转化效率，通过参数反演得到；i为生长天数。

式中：ETai为水分胁迫下的作物实际蒸散量（mm·d-1）；ETpi为作物潜在蒸散量（mm·d-1）；Sri为根系吸氮量（kg·hm-2·d-1），根据实际根系吸水量与土壤水溶液氮素浓度的乘积计算［33］；Smi为植株最低限度含氮量（kg·hm-2·d-1）；λ1、λ2分别为水分亏缺敏感指数和养分亏缺敏感指数；k1、k2、k3为经验系数，均通过参数反演得到。

2.3 参数反演

本研究利用Excel 规划求解工具中的演化算法反演确定待求参数。对霍泉站，将3 a共9个处理数据放在一起进行参数反演；对潇河站，将2 a 共6 个处理数据放在一起进行参数反演。反演参数主要包括土壤水分动态模拟中的参数和小麦产量模拟中的参数。

（1）土壤水分动态模拟参数反演，以实测土壤含水率及模拟土壤含水率误差平方和最小为目标函数，见式（19）：

式中：SWj为第j个处理所有模拟土壤含水率与实测土壤含水率的误差平方和；θij为实测土壤含水率（cm3·cm-3）；θ′ij为模拟土壤含水率（cm3·cm-3）；pj为j处理中实测土壤含水率的个数，i=1, 2,…，pj；j=1,2,…,m，其中m为规划求解所用到处理个数，霍泉站m=9，潇河站m=6。

待定参数包括土壤水分特性参数θs、θr、α、n、Ks以及水分胁迫参数h50、P、θwp、θj、A、B、C。演化时，根据已有的经验参数［31］，参照试验站的土壤质地确定3 组参数初始值，依次进行演化计算，可获得3 组待定参数，选定其中土壤含水率拟合误差最小的一组参数值作为初始值，再进行演化计算，当参数不再变化时停止演化计算。

（2）冬小麦生长动态及产量模拟参数反演，以茎、叶、籽粒模拟值与实测值误差平方和最小为目标函数，见式（20）：

式中：SYj为第j个处理中实测干物质重与模拟干物质重的误差平方和；YE、YJ、YL 分别为实测叶、茎、籽粒干重（kg·hm-2）；YE′、YJ′、YL′分别为模拟叶、茎、籽粒干重（kg·hm-2）；ej、gj、lj分别为j处理中叶、茎、籽粒实测干重样本的个数，o=1, 2,…,ej，q=1,2,…,gj，v=1,2,…,lj。

可变参数包括水分胁迫系数参数（k1、k2、λ1）、养分胁迫系数参数（k3、λ2）及光合产物转化效率（CVF）。为了获得更为准确的产量模拟结果，在式（20）的基础以产量模拟值与实测值误差平方和最小为目标（式21），进一步进行参数反演分析。

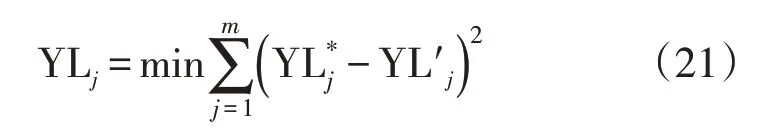
2.4 拟合精度评价

采用回归估计标准误差（RMSE）、相对误差（RE）、相关性系数（r）［38］对土壤含水率的模拟结果进行评价，r值越大，表明模型拟合效果越好，RMSE、RE 值越小，表明模拟值的精度越高。采用相关性系数对地上干物质的拟合情况进行评价，因收获时产量数据较少，采用相对误差对模拟产量结果进行评价，并利用F检验对不同水分胁迫响应函数模拟的产量进行差异性检验。

3 结果与分析

3.1 水分胁迫响应函数对0～60 cm土壤水分动态模拟的影响

通过式（19）进行参数反演优化，取最优演化结果，见表2、表3。由表可见，不同的水分胁迫响应函数条件下，利用试验资料反演得到的土壤水力特征参数、水分胁迫响应函数参数，没有明显的差异，且均在合理范围内［39］，如θs均大于田间持水率，且不超过0.5，表明了反演参数的合理性。

表2 土壤水力特征参数反演结果Tab.2 Inversion results of soil hydraulic characteristic parameters

表3 3种水分胁迫响应函数参数反演结果Tab.3 Three kinds of moisture stress response function parameter inversion results

利用反演的参数，可以得到不同土壤含水率模拟结果，对模拟值和实测值进行RMSE、RE和r的对比分析，结果见表4 及图1。由图表可见，不同水分胁迫响应函数条件下模拟结果的显著性检验均达到极显著水平，相关性系数r最小为0.7196，RMSE在0.0217～0.0363之间，表明土壤含水率模拟结果与实测值具有非常好的一致性。从霍泉站土壤含水率模拟结果看，VG 最好，其次为LS，MP 相对较差，表明S 型胁迫响应函数的模拟结果优于凹凸型函数；对于S 型曲线，基于土壤基质势的VG 要好于LS。从潇河站模拟结果看，土壤含水率相对误差大于霍泉站，平均RE 最大为12.47%；对比3种胁迫响应函数，MP计算的RE数值最小，另外2种函数对应的相对误差均值较大；潇河站土壤含水率相对误差变化范围较大，主要原因可能是中子仪测定土壤含水率过程中存在率定误差，盛钰［40］的研究中也出现了类似情况。

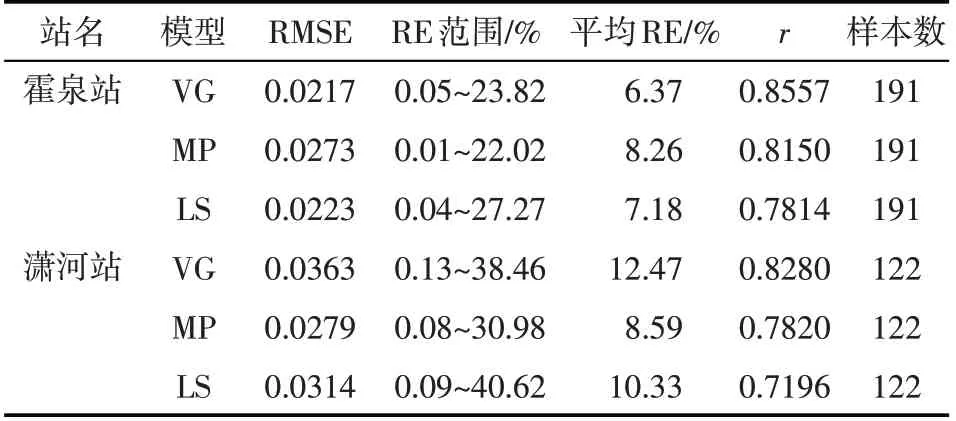
表4 不同水分胁迫响应函数模拟效果的评价Tab.4 Evaluation of simulation effects of different moisture stress response functions

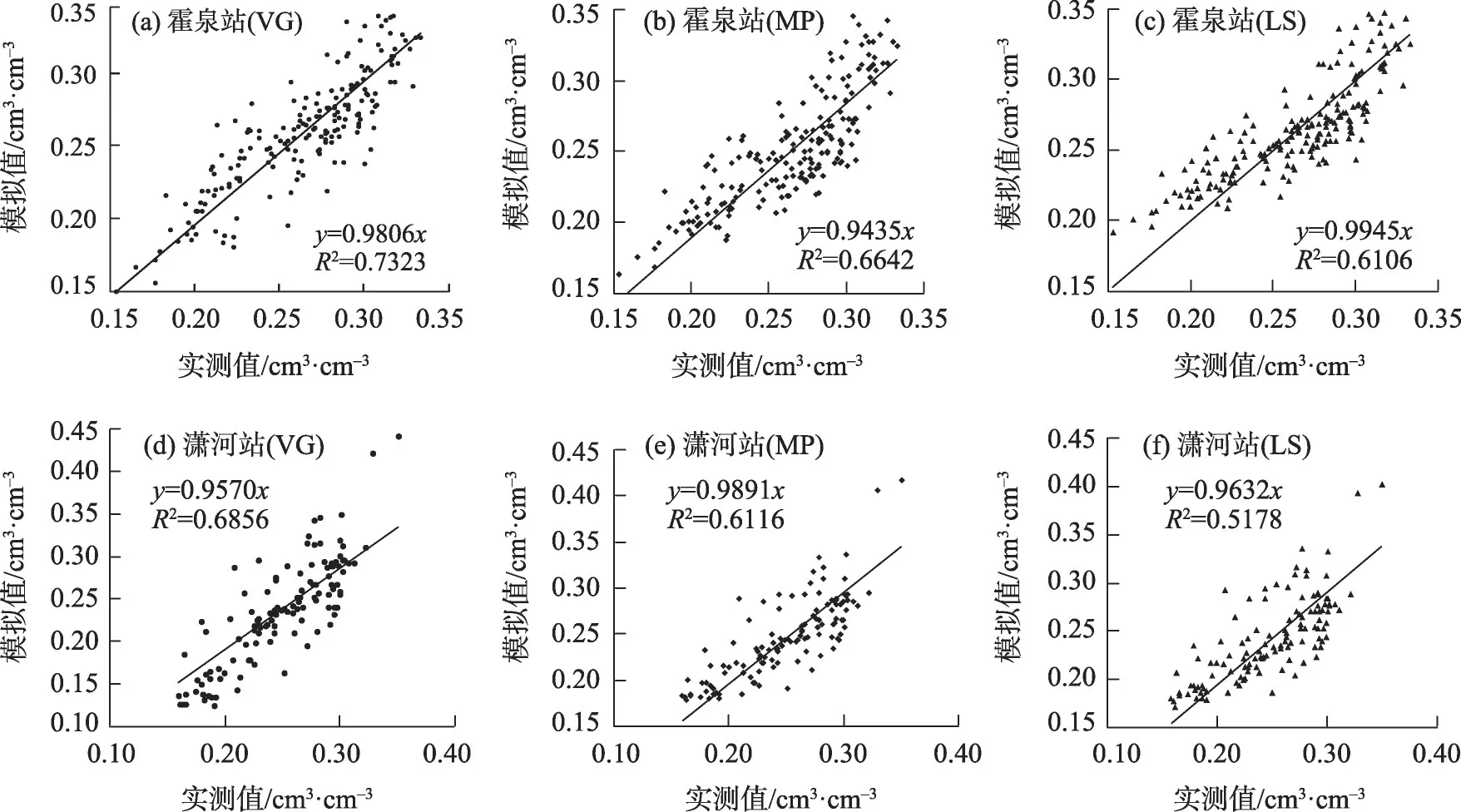
图1 基于3种水分胁迫响应函数的土壤含水率模拟值与实测值对比Fig.1 Comparison of simulated and measured water content values of three moisture stress response functions

3.2 水分胁迫响应函数对蒸腾量和蒸散量模拟的影响

水分胁迫响应函数对蒸腾量（Ta）及蒸散量（ETa）的模拟有明显的影响（表5）。由表5可见，使用VG 模拟的根系吸水量及ETa 明显高于另外2 种水分胁迫响应函数条件下的模拟值，且更接近实测值，2个试验站非常一致，不同处理也表现出了相同结果。这里ETa的实测值是利用水量平衡法计算求得，计算过程中没有考虑水分的深层渗漏及深层土壤水的补给。对于高水、中水的处理，灌水后根系层含水率较高，水分向下运移的数量相对较多，因而灌水处理实测的ETa 普遍大于模拟值；不灌水情况下，根系层含水率较低，对水分的吸持力较大，更容易发生深层土壤水的补给，因而霍泉站零水处理模拟蒸散量普遍大于实测值。

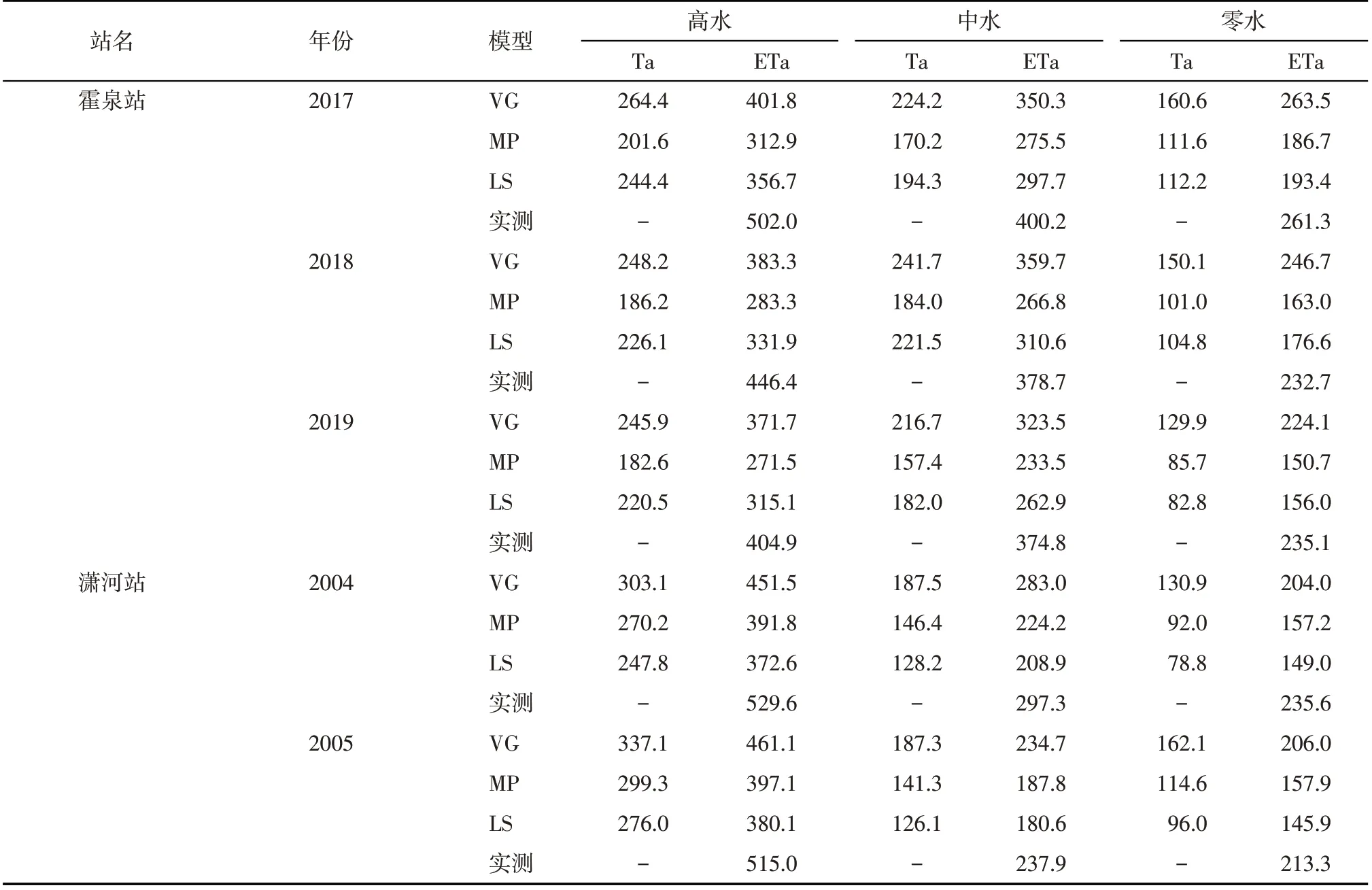
表5 不同水分胁迫响应函数下模拟的蒸腾量及蒸散量Tab.5 Simulated transpiration and evapotranspiration under different moisture stress response functions /mm

对于MP、LS 2 种水分胁迫响应函数，霍泉站采用MP模拟的Ta及ETa较低；而潇河站采用MP模拟结果明显大于LS 模拟值。说明MP、LS 受试验环境变化影响较大，存在不稳定性，相对而言VG使用效果好。

3.3 水分胁迫响应函数对产量模拟的影响

采用PS123 作物生长模型模拟作物产量，以霍泉站实测的地上干物质重数据反演了作物生长动态模拟参数，并给出了地上干物质模拟值与实测值的拟合程度检验结果，给出了最终产量模拟结果的相对误差（表6）。由表6可见，地上干物质重模拟值与实测值的相关性系数均在0.91 以上，r检验达到了极显著水平，表明模拟值与实测值具有很好的一致性，3 种水分胁迫响应函数都可以获得高精度的模拟结果。

由表6，VG、MP 及LS 的平均RE 分别为8.73%、8.40%及8.42%，产量模拟结果较为接近，图2 给出了模拟产量与实测产量对比情况。由图可见，3 种水分胁迫响应函数模拟值与实测值吻合程度较好，确定性系数在0.73以上，模拟点贴近1:1直线，表明产量模拟结果较好。对27 个模拟产量样本按不同的水分胁迫响应函数进行单因素的F检验，计算F值为0.0032，小于F0.01（5.61），表明根系水分胁迫响应函数确定性对最终产量模拟没有明显的影响。

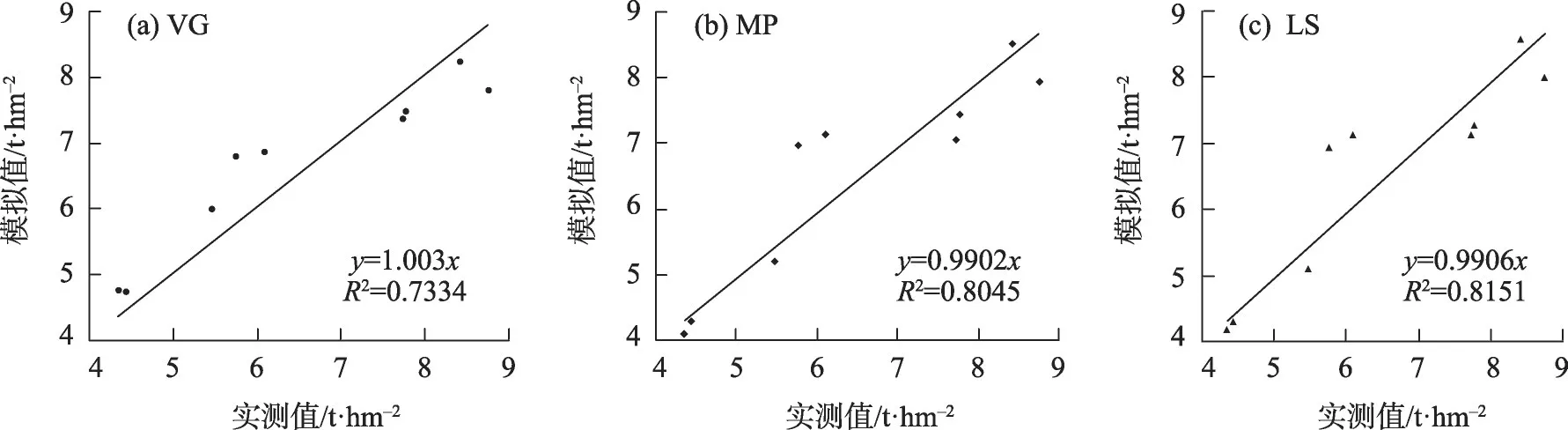
图2 产量模拟值与实测值对比Fig.2 Comparison of output simulation value and actual measurement value

表6 作物生长及产量模拟结果及评价Tab.6 Crop growth and yield simulation results and evaluation

4 讨论

水分是制约干旱区作物生长的主要因素，根系水分胁迫响应函数是根系吸水模型中的重要组成部分。通过评估不同形式水分胁迫响应函数的表征效果，有助于完善对根系吸水过程的处理。在作物产量水分关系中，根系水分胁迫响应函数通过以下过程影响土壤水动态、作物生长动态和产量的模拟。

利用参考作物蒸散量、作物系数、叶面积指数可计算潜在蒸腾量、潜在蒸发量。其中，潜在蒸发量通过上边界条件影响土壤水分运动，潜在蒸腾量通过根系吸水影响实际蒸腾量，同时根系吸水量也用于计算根系吸氮量。水分胁迫响应函数形式不同时，模拟的根系吸水效果不同，如吴训等［17］的研究表明，非线性胁迫响应函数相对于线性胁迫响应函数有更好的表征效果，本文进一步对比了非线性水分胁迫响应函数间表征效果，更好地反映了作物生长连续渐变过程。土壤基质势不受土壤分层影响，随深度变化是连续的，本文研究结果表明VG模拟水分变化优于另外2种函数。

作物吸收的水分、养分对生长发育及生物量积累具有显著影响，对此PS123 模型将不同影响因子分为了不同的生产潜力水平［36］，可采用实际蒸腾量与潜在蒸腾量的比值作为作物生长水分胁迫因子，采用根系吸氮量与植株最低限度含氮量的比值作为作物生长养分胁迫因子。蒸腾量与蒸发量较难进行准确区分［41］，实际蒸腾计算不准确将引起光合产物模拟误差增大，进而降低生物量模拟精度［42］，因而多数研究直接采用实际蒸散量与潜在蒸散量相比作为影响因子，如在FAO第33号灌排文件中给出的产量与水分响应转换关系中采用了实际蒸散量与潜在蒸散量的比值，这种经验关系使用较为广泛［43］。

植物光合产物分配系数模式［33］的建立可实现生物产量在根、茎、叶、籽粒间的分配，从而完成作物生长动态及产量的模拟。生物产量在根、茎、叶、籽粒间分配时也会受到水分、养分等环境因素的影响，即影响植株各器官的生长发育，这种影响又会反馈到潜在蒸散量与潜在生物量模拟中，对此张淑杰等［44］建立了动态作物系数计算方法取代了原本的固定作物系数。本研究着重对比水分胁迫响应函数形式，没有考虑作物系数动态变化对作物生长和产量模拟的影响，该处理对产量模拟没有造成过大误差，如康国芳［45］模拟的冬小麦产量平均相对误差为7.10%；王伟等［46］采用CERES-Wheat 模型预测冬小麦产量，4 a 平均相对误差为9.42%，同本研究给出的相对误差（8.40%～8.73%）接近。

不同的水分胁迫响应函数形式没有对产量模拟产生明显的影响，主要是因为水分胁迫系数、养分胁迫系数的参数反演，在一定程度上修正了蒸散量、吸氮量对作物生长动态及产量的影响。利用反演模型推求土壤水分特征参数已成为近些年的研究热点［47-48］，相对室内试验的方法，参数反演获得的参数在一定程度上概化了不同空间点的差异。另一方面，参数反演对作物生长模型中非保守参数的率定也有很大作用，通过率定可以使模型本地化，显著提高模拟精度［42］。

5 结论

（1）采用VG、MP 及LS 都可以获得较好的土壤水分模拟结果及产量模拟结果，相关性系数值均在0.71以上，土壤含水率模拟值与实测值的平均RE小于12.5%，模拟产量的平均RE小于8.8%。

（2）就土壤水分动态模拟效果而言，S型水分胁迫响应函数好于凹凸型水分胁迫响应函数，VG 水分胁迫响应函数又好于LS 水分胁迫响应函数。采用VG水分胁迫响应函数得到的蒸散量更能反映实际情况。

（3）本研究中提出的LS 水分胁迫响应函数很好的避免了分段函数中速率突变问题具有较好的模拟效果，但是其随环境变化的稳定性还有待进一步研究。