基于突出“局部差异”—TOPSIS法的沥青路面养护效果分析
王晨韬,刘尊青,谢海巍,敖茂川
(新疆农业大学 交通与物流工程学院,乌鲁木齐 830052)
路面使用性能评价是利用路面状况数据,对路面性能是否满足使用要求做出的评价。路面性能评价不仅是进行沥青路面养护的前提,也是路面使用性能预测和养护措施选择的重要参考,同时,也是进行养护方案施工后评价的重要依据。
国外对建立道路评价模型的探索开始较早,世界上第一个较为完善的路面使用性能评价模型为PSI模型,该模型是美国各州公路与运输工作者协会(AASHTO)基于10年实验数据而提出,该模型提出了路面平整度对路面使用性能的影响[1];日本在PSI模型的基础上提出了侧重从公路管理层角度出发的MCI路面评价模型[2],主要通过路面破损状况和车辙来反映道路行驶质量;Saaty[3]提出的层次分析法是把复杂问题进行定性与定量相结合的权重分析,可应用到路面性能评价中;Rahman等[4]利用回归技术开发了8个路面评价模型,用于South Carolina地区不同路面的使用性能评价。
我国较早的高速公路路面使用性能评价模型为交通运输部公路科学研究院提出的RIOH模型。之后,潘玉利等[5]在此模型基础上建立了针对杭州市的路面状况评价模型。现常采用路面技术状况指数PQI对路面使用状况进行评价,该模型具有各指标分配明确、计算过程简单等特点,但由于各地区公路在气候、交通量、路面材料等方面不尽相同,因此,将各地区公路路面使用性能评价指标的权重系数完全统一时,可能使评价结果不能准确反映路面使用状况。近年来,不同学者采用多种方法对路面使用性能进行研究。Wang等[6]建立了灰色聚类分析评价模型,并将其应用到路面使用性能评价中;Ling等[7]将可拓理论应用于路面使用性能的分析中;Yan等[8]运用粒子群优化与支持向量机相结合的方法评价路面使用性能;Fan等[9]构建了一种基于专家评价的层次分析方法来评价路面使用性能;李清富等[10]利用灰色聚类重新分配指标权重,讨论了灰色聚类决策在路面性能评价中的应用;刘秀菊等[11]应用灰色系统理论模型,建立了基于历史数据的指标预测模型,并对模型的精度进行了评价;元松[12]用层次分析法对路面使用性能进行综合评价;李国强、曹志等[13-14]利用模糊数学法建立了模糊综合评价模型;潘怀兵、杨明等[15-16]将主成分分析法应用于沥青路面使用性能的综合评价。除此之外,胡霞光等[17]在路面检测数据与专家综合评价之间建立回归模型,再用遗传算法对模型进行优化,从而对路面使用性能进行评价;王惠勇等[18]用物元模型对路面状况进行评定,并加以验证,证明了物元模型对路面使用性能评价的实用价值。
文中先将突出“局部差异”法进行优化,然后再与TOPSIS法结合[19]来评价我国新疆吐鲁番某高速公路沥青混凝土路面的综合使用性能,对采取不同养护措施的路段进行养护后评价。
1 基于突出“局部差异”的TOPSIS法
1.1 突出“局部差异”法
突出“局部差异”法是漆艳茹[20]提出的一种确定指标权重的方法,该方法体现的指标重要程度为同一指标数值之间的差异程度。在某一个评价系统中,若某一项指标的数值之间差异性大,则说明其对被评价对象的影响大,用突出“局部变异”法所得出的权重大;反之,某一项评价指标的数值之间差异性越小,说明此项指标对该评价系统的结果影响较小[21]。
指标权重的确定通常有以下步骤:
步骤1 先设评价对象集O={o1,o2,o3,…,on},指标集P={p1,p2,p3,…,pn},方案Oi关于指标Pj的取值Xij=Xj(Oi)(i=1,2,…,m;j=1,2,…,n),这里假设各指标的值均大于0,则评价对象集O关于指标集P的指标值矩阵为
(1)
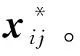
(2)
步骤3 再利用均差法求权重
(3)
其中
(4)
(5)

1.2 TOPSIS法
TOPSIS法是将原始数据经过同向化、归一化后,寻找所得矩阵中的最优方案和最劣方案,然后再求出所求对象与最优、最劣方案的差距,以此评价所求对象的好坏,最佳方案就是离最优方案最近的解。
TOPSIS的算法步骤:
步骤1 构造初始评价矩阵。假设多属性决策问题有n个待评价对象,其中每个评价对象对应有m个评价指标,将评价对象的原始数据组成矩阵X=(xij)m×n,算式为
(6)
步骤2 构造标准化矩阵。对原始数据组成的矩阵X=(xij)m×n进行同向化、归一化,可得到矩阵
(7)
对于效益属性来说则有
(8)
对于成本属性来说有
(9)
步骤3 得出最优、最差向量。根据下式可得出矩阵Y各列最大值和最小值构成的最优、最差向量为
Z+=(Zmax1,Zmax2,…,Zmaxn)
(10)
Z-=(Zmin1,Zmin2,…,Zminn)
(11)
步骤4 计算各方案与最优、最劣向量的距离
(12)
(13)
步骤5 第i个对象与最优方案的接近程度。接近程度Ci的算式为
(14)
步骤6 对各个方案按照Ci的大小进行排序,Ci的值越大,说明此方案越接近理想值,且与最优向量越接近。
2 工程应用
2.1 项目背景
现以我国新疆吐鲁番G3012高速公路中一段养护维修工程所采集的数据为依托进行研究。2017年对G3012高速的上行线路段进行大中修养护工程,该项目路线起点位于小草湖服务区以南约2 km、桩号K0+000,终点位于托克逊县以南45 km、桩号为K80+000,路线全长80 km。该项目对K0+000~K39+911段实施的养护措施为:旧路铣刨3 cm+加铺4 cm AC-16C橡胶沥青;对K39+911~K80+000段实施的养护措施为:旧路铣刨4 cm+加铺5 cm AC-16C橡胶沥青,且同步碎石封层用于K0+000~K51+000段,防水防裂基布用于K51+000~K80+000段。养护项目完工后已通车4年,路面使用性能均有一定程度的衰减,现基于2021年采集的路面技术状况指标数据进行分析。
两段路面养护均选用铣刨罩面,但具体措施不同的路段中分别选择其中具有代表性的5 km数据,将其命名为A段与B段。利用上文中提到的突出“局部差异”—TOPSIS法进行分项指标权重及路面使用性能分析。具体路段的路面技术状况指标如表1所示。
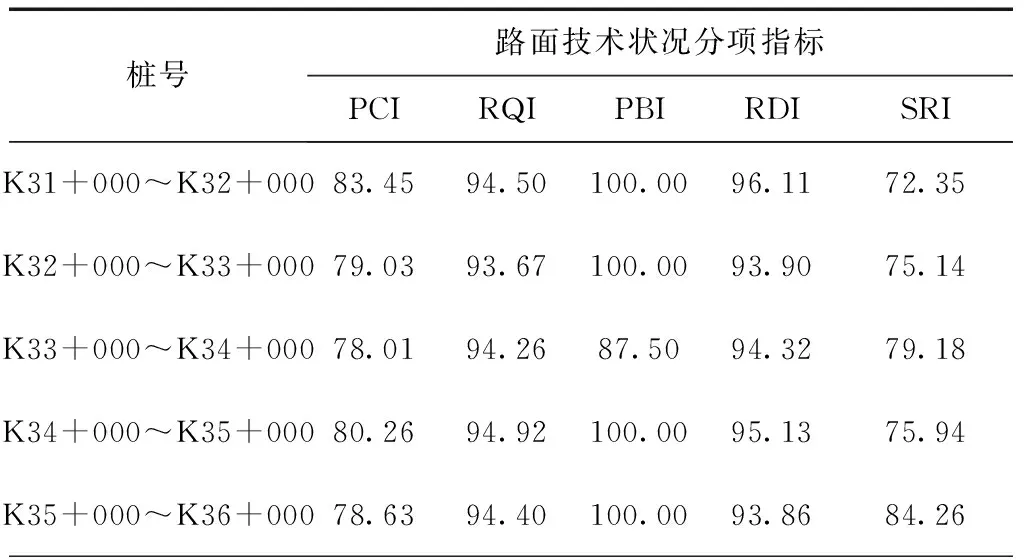
表1 路面技术状况指标
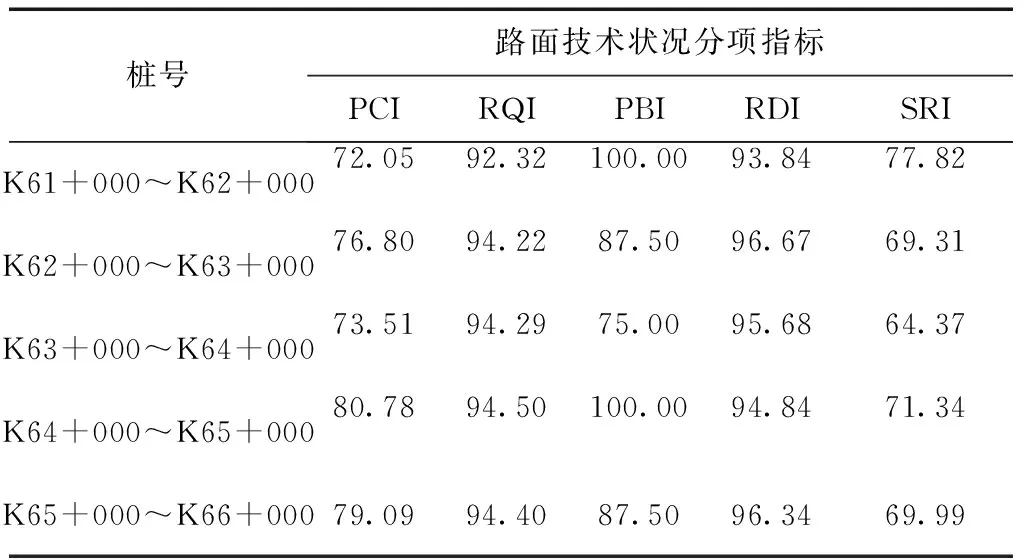
桩号路面技术状况分项指标PCIRQIPBIRDISRIK61+000~K62+00072.0592.32100.0093.8477.82K62+000~K63+00076.8094.2287.5096.6769.31K63+000~K64+00073.5194.2975.0095.6864.37K64+000~K65+00080.7894.50100.0094.8471.34K65+000~K66+00079.0994.4087.5096.3469.99
2.2 突出“局部差异”法的运用与优化
2.2.1 利用突出“局部差异”法确定指标权重
根据表1中的数据,结合上文中提到的突出“局部差异”法的计算方法,可得到矩阵A与矩阵B为


根据式(2)对矩阵A与矩阵B进行无量纲化,可得到新矩阵,记为矩阵A1与矩阵B1,即
A1=

B1=

矩阵A1:利用式(4)、式(5)进行计算可得
σ1=0.024 8;σ2=0.004 3;σ3=0.057 1;
σ4=0.009 1;σ5=0.056 3
根据式(3)计算可得到各指标权重
ω1=0.163 3;ω2=0.028 5;ω3=0.376 8;
ω4=0.060 1;ω5=0.371 3
由计算结果可知,路面损坏状况指数PCI被赋予的权重系数为0.163 3,路面行驶质量指数RQI被赋予的权重系数为0.028 5,路面跳车指数PBI被赋予的权重系数为0.376 8,路面车辙深度指数RDI被赋予的权重系数为0.060 1,路面抗滑性能指数SRI被赋予的权重系数为0.371 3。
矩阵B1:利用式(4)、式(5)进行计算可得
σ1=0.045 5;σ2=0.008 9;σ3=0.124 7;
σ4=0.011 0;σ5=0.067 2
根据式(3)计算可得到各指标权重
ω1=0.177 0;ω2=0.034 5;ω3=0.484 8;
ω4=0.042 6;ω5=0.261 2
由计算结果可知,路面损坏状况指数PCI被赋予的权重系数为0.177 0,路面行驶质量指数RQI被赋予的权重系数为0.034 5,路面跳车指数PBI被赋予的权重系数为0.484 8,路面车辙深度指数RDI被赋予的权重系数为0.042 6,路面抗滑性能指数SRI被赋予的权重系数为0.261 2。
考虑到在实际路面使用过程中,路面破损情况对路面性能的影响最大,这与JTG 5210-2018《公路技术状况评定标准》(以下简称《标准》)[22]对PCI所占权重的分配原则一致,所以将突出“局部差异”法计算出的权重系数用《标准》中各指标的权重系数进行加权计算,计算结果如表2所示。
由表2可得,进行加权计算后主要是PCI所占的权重增加、PBI的权重系数减少,这正与《标准》中各指标权重的分配理念相同。下面对路面技术状况指数PQI的值进行计算,以验证优化后算法的可行性。

表2 A、B路段优化前后各指标权重系数
2.2.2 利用优化后的突出“局部差异”法计算PQI
分别用传统方法、突出“局部差异”法、优化后的突出“局部差异”法计算路面技术状况指数PQI,文中所说的传统方法为《标准》中介绍的PQI算法,具体权重系数的赋值为式(15)所示。
PQI=0.35PCI+0.3RQI+0.15RDI+
0.1PBI+0.1SRI
(15)
根据式(15)与上文中计算出的权重系数可得表3与表4。
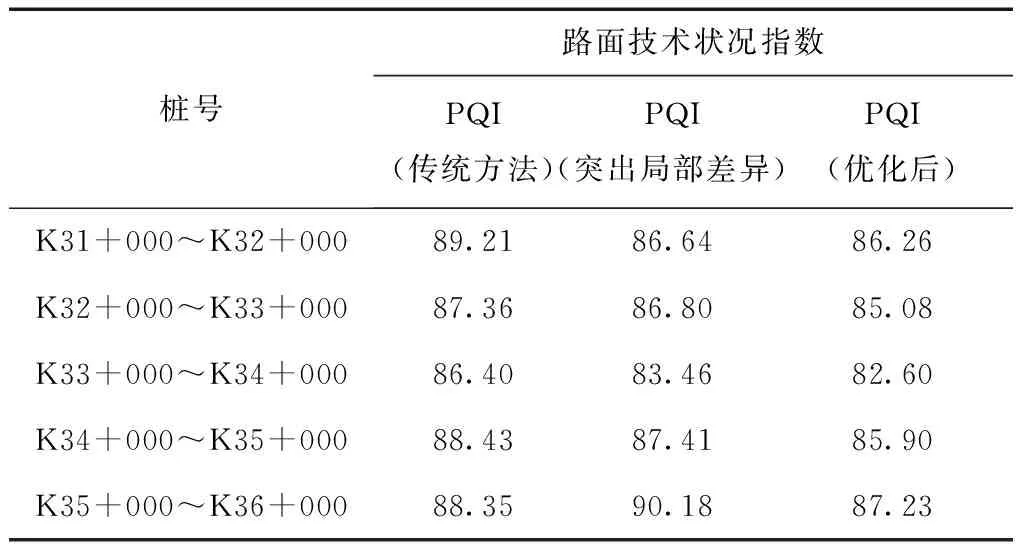
表3 A段PQI值

表4 B段PQI值
在路段A中,利用传统方法计算出的PQI均值为87.95;利用突出“局部差异”法计算出的PQI均值为86.89;优化计算后PQI的均值为85.42。
在路段B中,利用传统方法计算出的PQI均值为85.32;利用突出“局部差异”法计算出的PQI均值为82.90;优化计算后的PQI均值为81.71。
2.2.3 突出“局部差异”法及其优化算法分析
用突出“局部差异”法进行分项指标的权重系数重新赋值时,发现无论是路段A还是路段B,该算法均将路面跳车指数PBI所占的权重系数放在首位,其次是路面抗滑性能指数SRI的权重系数。根据经验判断,在对分项指标所占权重进行赋值时,着重考虑的应该是对路面使用性能影响较大且数值较低的PCI。此时可以看出,若单纯用突出“局部差异”法计算各分项指标的权重系数稍显不合理。经分析发现PBI的权重系数被放大的根本原因是该组数据极差为所有指标中最大,即该算法在计算权重系数时突出表现的是数值变化幅度大的指标,而忽视了数值本身的大小,所以,该算法比较适用于各分项指标数值变化相对平稳的情况,而在数值变化大或数值本身基数小的情况则表现出了一定的局限性,并不能准确将路面的实际情况反映出来。文中结合《标准》中各分项指标的权重系数对其进行优化计算。
计算结果发现,优化后计算得到的PQI值相对较低,主要原因是该算法将指标等级划分整体为优的RDI与RQI所赋予的权重降低,将性能表现较差、等级划分整体为中的PCI与SRI所赋予的权重增加。优化后的权重系数可以更准确地将影响路面使用性能的指标反映出来,优化算法既保留了突出“局部差异”法的特点,又与传统方法相结合,在实际道路状况的基础上客观体现了评价指标在评价过程中的影响程度。
2.3 利用TOPSIS法进行计算
根据《标准》中对PCI、RQI、RDI、PBI、SRI的等级划分,可将其分为优、良、中、次、差五个等级,将其指标划分标准与表1数据相结合构成矩阵XA与XB
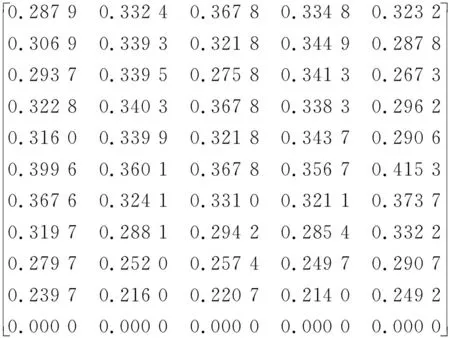
根据式(7)对以上两个矩阵进行同向化、归一化变化,得到矩阵YA、YB为
YA=

YB=
根据式(10)、式(11)可用上述矩阵各列中的最大、最小值构成最优、最差向量

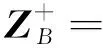
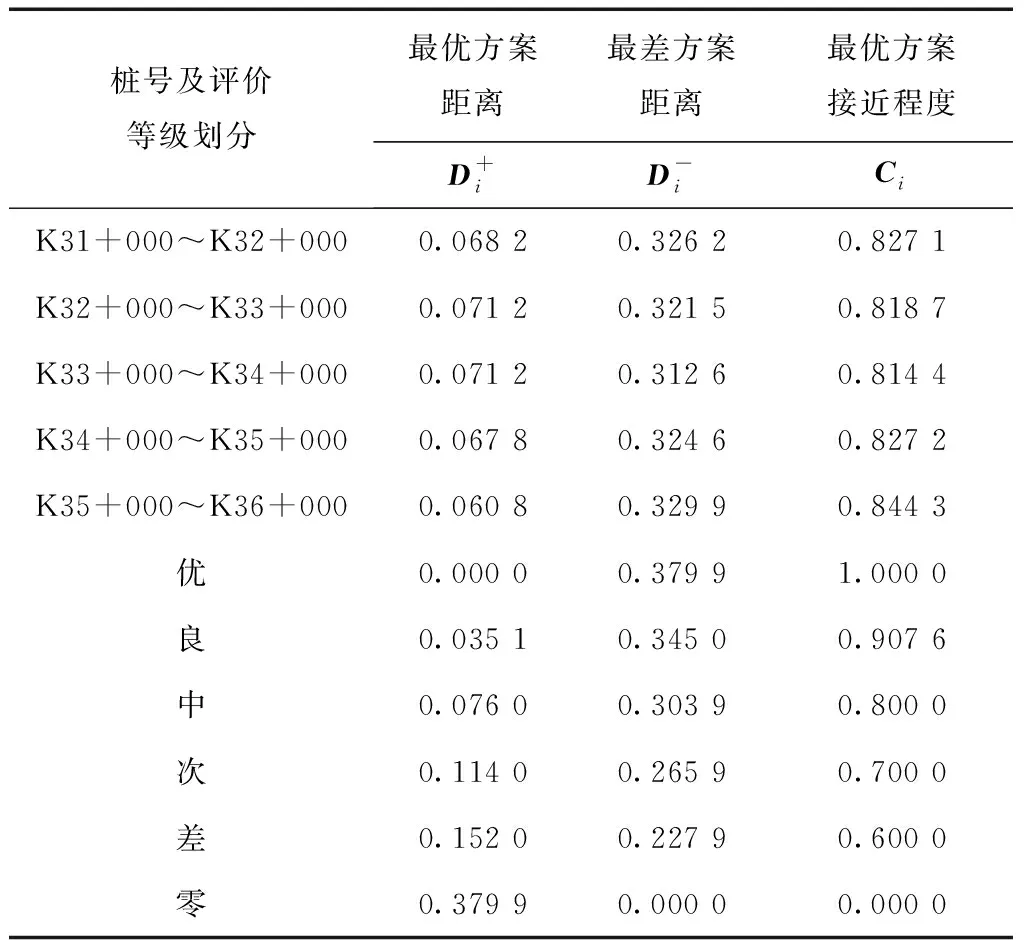
表5 A段各路段与最优、最差向量的距离及接近程度
根据表5可得,在路段A中,利用突出“局部差异”—TOPSIS法计算得出路面使用性能表现最好的是K35+000~K36+000段,而路面使用性能表现最差的路段为K33+000~K34+000段,整个A段与最优方案接近程度的均值为0.826 3。
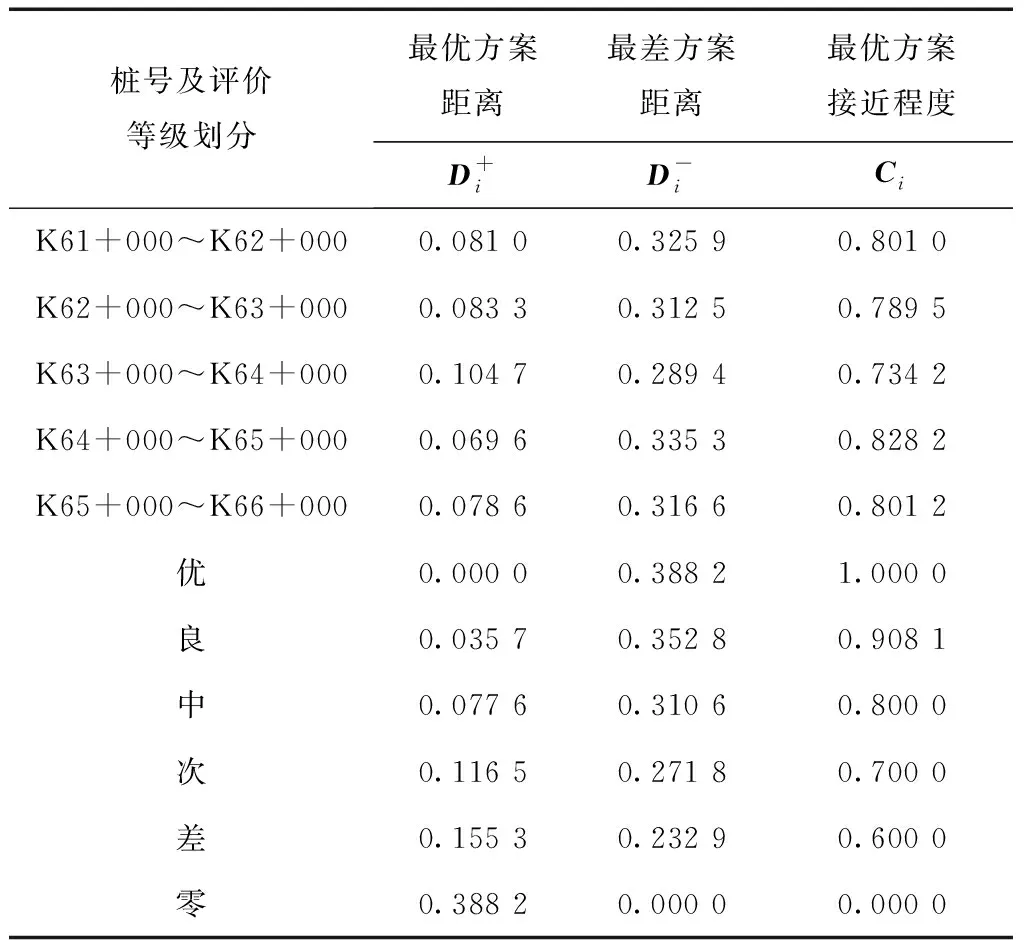
表6 B段各路段与最优、最差向量的距离及接近程度
由表6可得,在路段B中,利用突出“局部差异”—TOPSIS法计算得出路面使用性能表现最好的是K64+000~K65+000段,而路面使用性能表现最差的路段为K63+000~K64+000段,整个B段与最优方案接近程度均值为0.790 8。
根据优化后的突出“局部差异”—TOPSIS法计算得出的路面使用性能结果表明,在养护项目完工通车4年后,养护措施为“旧路铣刨4 cm+加铺5 cm AC-16C橡胶沥青+同步碎石封层”的A路段路面使用性能较好,与传统方法求得结果相一致,说明优化后突出“局部差异”—TOPSIS法具有一定的适用性,之后在该地区的其他路段进行铣刨罩面时,可参考路段A的养护方案。
3 结 论
1)突出“局部差异”法计算目标权重时着重表现的是数值的变化幅度大小,且该算法在计算时忽略了数值本身大小。将该算法计算出的权重系数用《标准》中规定的各指标系数进行加权,可使计算出的结果更贴合实际路面使用状况。
2)无论是运用《标准》中的方法计算出的PQI值,还是用优化后的突出“局部差异”—TOPSIS法计算得出的各路段与最优方案的接近程度,均说明A路段的路面使用性能表现更好,即养护措施为“旧路铣刨4 cm+加铺5 cm AC-16C橡胶沥青+同步碎石封层”的A路段养护效果更好。该地区的其他路段在之后进行养护施工时,可参考A路段的养护措施进行路面养护方案选择。

