考虑乘客出行路径的多线路公交时刻表优化
许 莹,邹常丰,贾佃精,赵博佳,刘 委
(1.东北林业大学 交通学院,哈尔滨 150040;2.辽宁省交通运输事业发展中心,沈阳 110003)
公交调度是提高公交运营效率的重要途径,具有较大提升潜力,同时,合理设计公交时刻表不仅可以降低公交公司的运营成本,而且可以保证乘客的便利性。
近年来,交通运输领域学者针对城市公交调度优化问题,从模型优化、算法改进等方面开展了深入研究。Nam等[1]考虑车辆燃油量和碳排放因素,以环境成本最小为目标函数建立公交调度模型;Ibarra-Rojas等[2]对偏离路线及发车间隔的车辆予以惩罚,建立时刻表优化模型;熊昕宇[3]考虑不同道路情况对公交车运行的影响,建立了公交车辆运行状态预测模型;张莉[4]考虑在实际运营过程中的不同条件,建立组合优化模型,选用遗传和模拟退火算法,实现对算法的优化和模型求解;Saharidis等[5]考虑特定时间段内的高乘客需求,提出以乘客候车时间最小为目标的混合整数线性规划方案;Kang等[6]提出了一种考虑公交驾驶员休息窗口时间的公交时刻表优化模型;Carosi等[7]考虑发车间隔和车辆调度的影响,设计了一种区域公交调度集成模型;张海燕等[8]将公交时刻表优化转化为发车间隔优化,建立了公交时刻表优化模型;任俊[9]在公交系统大数据背景下,对公交数据进行深入分析,在此基础上构建基于动态需求的单线公交时刻表优化模型;Wu等[10]考虑松弛时间,建立了巴士时间限制与随机旅行时间随机整数模型,并运用GALS与OPM模型进行迭代优化,最大限度地降低不同类型乘客的总等待时间成本;罗淩珊等[11]考虑疫情对公交调度的影响,以降低病毒传播风险和社会经济运行损失为目标建立非线性时刻表优化模型;胡金成[12]考虑公交运行效能,建立双层规划模型;张姚等[13]考虑换乘站点的时间权重最小化,建立多目标时刻表优化模型。
考虑多线路重叠运行情况:汤茹茹[14]建立一种多车型组合调度模型,在不同运行区间采取相应的车型运行;姜楠[15]考虑公交车跨站、跳站等车辆调度方式对乘客总出行时间的影响,建立公交调度模型;宋现敏[16]考虑在重叠区间包含多个运营商,提出一种双层规划模型。
优化算法改进方面:朱鹰屏等[17]应用改进的双中心粒子群优化算法对建立的电动公交车馈电线路模型进行优化;滕靖等[18]考虑可调度车辆数对纯电动车续航能力的影响,建立公交时刻表优化模型,并利用粒子群算法进行求解;赖元文等[19]以多线路公交公司盈利最大和乘客出行时间最短为目标,建立公交调度优化模型,并利用模拟退火—自适应布谷鸟算法对模型进行求解;Jin等[20]根据公交历史轨迹数据,计算站间实际行车时间,并基于各站乘客上下车人数,运用混合算法和模拟退火算法优化发车时刻表。
上述文献中,考虑多线路重叠情况对公交调度影响的较少。应在保障公交公司基本盈利的情况下,考虑公交廊道的情况,尽可能缩短乘客出行时间。
文中考虑多线路重叠运行情况,根据乘客的不同出行路径,将乘客分为两类,并以公交运营利润最大和乘客出行时间最小为目标函数,建立多目标公交调度优化模型,并通过模拟退火—非支配排序遗传算法求解,得到最优发车间隔。
1 时刻表优化模型建立
1.1 问题描述
乘客通过公共交通完成出行活动的出行路径可根据其上车、下车的站点来判断。基于公交运行区间的重叠情况,将公交运行线路划分为3个部分,分别为运行区间一、运行区间二和运行区间三,如图1所示。运行区间一为始发站到多线路重叠运行区间的前一个站点;运行区间二为多线路重叠运行区间;运行区间三为多线路重叠运行区间后的第一个站到终点站。

图1 公交线路运行区间划分
根据出行路径将乘客分为两种,第一种为上、下车行为均在运行区间二内站点完成的乘客,第二种为上、下车行为最多有一个是在运行区间二内站点完成的乘客。其中,第一种乘客在重叠站点内可以选择任意的公交线路完成出行,为节约乘客出行时间,可选择先到达候车站点的公交车完成出行;而第二种乘客只能选择单一的公交线路完成出行。
为简化问题并保证模型仿真过程在稳定环境中进行,本文假设如下:
1)乘客到达站点服从均匀分布;
2)公交车辆沿规定路线行驶;
3)同一线路车辆经过相同路段所用时间相同;
4)各线路公交车的车厢容量一致。
1.2 模型建立
共有I条公交线路在线网中,用i=1,2,3,…,I表示;公交线路i有Gi个站点,用g=1,2,3,…,G表示。其中,有O个站点在多线路重叠运行区间内,有Ri个站点在多线路重叠运行区间前,每条公交线路共有Qi辆公交车。
乘客出行时间为站点候车时间与车内行程时间之和,公交运营利润为公交公司的运营收益与运营成本之差。
1.2.1 乘客站点候车时间

(1)
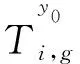

(2)
乘客站点候车时间为两种乘客的站点候车时间之和。第一种乘客站点候车时间t1为新到乘客与上一辆公交车滞留乘客的站点候车时间之和,即
(3)
同理,第二种乘客的站点候车时间为
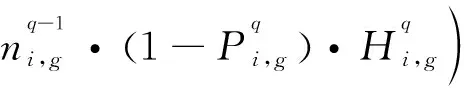
(4)

1)站点停靠时间。站点停靠时间由车辆开门时间、乘客上下车时间以及关门时间3部分组成。其中,乘客上下车时间由乘客上车与下车时间的最大值决定[21],即
(5)

2)站点上下车乘客数。站点上车乘客数由经过站点时的车厢容量决定。站点的实际上车乘客数为候车人数与车厢剩余容量的最小值,站点车厢剩余容量为车厢总容量与站点下车人数之和减去站点车厢内人数。所以上车乘客数表示为
(6)

站点下车乘客数与站点的平均下车率有关,即
(7)

(8)
(9)

(10)
式中:Si,g为站点g-1到站点g的路段行程时间;te,tf分别为减速进站时间和加速离站时间。
1.2.2 乘客车内行程时间
车内行程时间t3为乘客在站点上车后,到达目的站点下车这一过程所需要的时间,算式为
(11)
1.2.3 公交运营成本
公交运营成本C1主要包括车辆维修费、人员薪资和设备费用等固定成本以及车辆燃油耗能成本,可用单位公交车每千米的运行费用[22]表示,即
(12)


(13)
1.2.4 公交运营利润
公交运营利润C2主要为运载乘客的收入,为公交线路所有上车乘客与票价的乘积,即
(14)
式中:E为票价。
1.3 建立目标函数
1)乘客出行时间。乘客出行时间t由第一种、第二种乘客的站点候车时间以及车内行程时间组成。
mint=t1+t2+t3
(15)
2)公交运营利润。公交运营利润C为公交运营收益与公交运营成本之差,即
maxC=C2-C1
(16)
3)约束条件。公交车的发车间隔必须满足最大和最小发车间隔,即
(17)
公交调度时,保障公交公司的收入大于支出,公交运营利润大于0,即
C≥0
(18)
根据公交车容量的限制,车厢内乘客数应小于公交车厢容量,即
(19)
综合各目标函数,得到多目标公交调度优化模型
mint=t1+t2+t3
(20)
(21)
2 模拟退火—非支配排序遗传算法
非支配排序遗传算法(NSGAⅡ)[23]是一种基于NSGA改进的多目标优化算法。模拟退火算法(SA)将随机因素引入最优解搜索过程中,在迭代更新过程中,跳脱出局部最优解的范围,以一定概率搜索到全程最优解[24]。
模拟退火—非支配排序遗传算法(SA-NSGAⅡ)具有以下优点:
1)相较于非支配排序遗传算法(NSGA)计算复杂度降低、准确性提高,且pareto解集分布均匀。
2)相较于NSGAⅡ算法,在个体选择时以一定的概率将拥挤度较小的个体储存到遴选集中,从而防止丢失非劣解。
3)在MATLAB软件中进行优化求解时,运行效率较高、稳定性更好。
因此,文中选用模拟退火—非支配排序遗传算法寻求最优发车间隔。
2.1 模型在算法中的处理
1)对于多线路重叠运行区间,第一种乘客和第二种乘客的站点候车时间需分别计算,车内行程时间需根据乘客选择的公交线路路段行程时间以及站点停靠时间确定,选择的公交线路不同,车内行程时间也不同。因此,在应用MATLAB编写程序时,综合考虑乘客在各重叠站点内的上下车情况,计算站点候车时间以及车内行程时间。
对于非多线路重叠运行区间,即运行区间一和运行区间三,乘客根据出行目的仅可选择固定的公交线路,各站点全部为第二种乘客,只计算第二种乘客的站点候车时间以及车内行程时间。因此,在应用MATLAB编写程序时,根据公交车的运行状况计算第二种乘客的站点候车时间以及车内行程时间。
2)为方便模型处理,将规定时间段内发车间隔的约束条件转化为最大和最小间隔发车数,确定线路的车辆数范围。
3)因站点乘客候车乘客数与车头时距相关,但每条线路首辆公交车无车头时距,所以规定首辆公交车的车头时距用路段行程时间表示,其余车辆的车头时距用发车间隔的相应算式表示。
2.2 算法基本步骤
1)设置算法参数。初始温度为T0,初始化种群为P1,种群规模为N,初始迭代次数为0,设置最大迭代次数、交叉率、变异率、温度下降速率。
2)输入模型参数。输入站点上车率、下车率、路段运行区间、第一种乘客和第二种乘客比例数等数据。
3)计算种群P1中所有个体的非支配排序Kj和拥挤度Rd。
4)个体选择。对任意个体i1和i2,若Ki1>Ki2,则将个体i1储存在遴选集M1中。若Ki1=Ki2,则采用Metropolis准则进行判断见式(22),当Ri1>Ri2,则将个体i1储存到遴选集M1中;当Ri1≤Ri2,则以一定概率ρ将个体i2储存到遴选集M1中,直至M1的个体数达到N。算式为
(22)
5)通过交叉、变异等操作使遴选集M1中的个体产生子代种群Q1。
6)将子代种群Q1与P1合并在一起,组成种群规模为2N的新种群S1。
7)计算S1种群个体的非支配排序和拥挤度,将非支配集的个体按照从高到低的序列依次放到新的父代种群P2中[25],若某一层的非支配个体放到P2后,种群规模超过N,则将该层个体按照拥挤度从大到小的顺序放入P2中,直至P2的种群规模达到N。
8)达到最大迭代次数后终止循环,输出帕累托前沿解集;若未完成迭代,循环步骤4)—步骤7),直至完成迭代。
3 实例分析
3.1 案例概述
为验证模型的实用性,以哈尔滨市10路、56路、68路、75路、117路和102路公交线路为例。以上6条公交线路均在和兴路路段有重叠运行区间,重叠运行区间内包含林业大学、林业总医院、林兴路以及哈师大4个站点。各公交线路的基本信息如表1所示,线路如图2所示。

表1 公交线路信息表

图2 公交线路
采用人工调查法采集公交客流数据,调查时间选择晚高峰16:30—17:30,跟车采集各站点的上下车乘客数、站间行程时间和发车间隔等数据,驻站调查多线路重叠区间第一种乘客、第二种乘客的比例。以10路公交为例,对调查数据进行整理计算,计算结果如表2、表3所示。

表2 哈尔滨10路公交数据

表3 第一种乘客比例 %
3.2 模型及算法参数标定

通过多次测验,将SA-NSGAⅡ算法中的各个参数设置如表4所示。

表4 部分参数标定
3.3 结果分析
运用MATLAB软件对上述模型进行优化,得到4组发车间隔优化方案。4组优化方案对应的目标函数值如表5所示,并以优化方案3为例,得到各线路发车时刻表,如表6所示。

表5 公交线路调度方案
由表5可知,4种优化方案相较于原始方案,乘客出行时间均缩短,公交运营利润均有所提升。其中,优化方案3缩短乘客出行时间最多,较原始方案缩短13.8%;优化方案4公交运营利润提升最大,增加6.9%。

表6 发车时刻表
4 结 论
文中根据乘客出行路径不同,将乘客分为两种,并充分考虑两种乘客的特点,构建公交运营利润最大和乘客出行时间最短的多目标时刻表优化模型,运用模拟退火—非支配排序遗传算法,以哈尔滨市6条公交线路为例,得出6条公交线路的发车间隔以及不同优化方案的目标函数值。优化结果表明:4种优化方案相较于原始方案,乘客出行时间均缩短,公交运营利润均有所提升,验证了模型的有效性和实用性。

