机器学习技术在曹娥江流域洪水预报中的应用
孙小洪,赵 兵,孙逸群,石 朋
(1.上虞区虞东水闸运行管理中心,浙江 绍兴 312300;2.信阳市南湾水库管理局,河南 信阳 464031;3.河海大学水文水资源学院, 江苏 南京 210098)
1 问题的提出
洪水预报是应对洪涝灾害预警最重要的非工程措施[1],国内外学者围绕水文模型展开大量的研究[2-4]。水文模型通常可分为数据驱动模型、概念性模型和物理模型[5-7]。概念性模型和物理水文模型基础为水循环,建模人员对水文过程物理机制的理解程度和模型对物理过程描述的精细程度是制约模型效果的关键。然而,受人类自身认知能力的限制、气候异常变化和人类活动等因素的综合影响,传统的模型方法仍有很大的改进空间。基于机器学习技术的预报模型因不需要深入理解和描述降水—径流各个关键环节,且建模过程相对简单而备受关注。Kim等基于神经网络模型,建立一种适用于无资料地区的、以卫星遥感数据作为模型输入的神经网络模型。李鸿雁等[8]在总结大量洪水预报实践经验的基础上,提出一种改进BP算法。熊立华等[9]使用神经网络技术建立一种权重系数可以在每一时间步长上进行自动更新的洪水预报模型。邱超[10]基于聚类分析和模糊数学的基本原理,采用基于加权的模糊聚类新算法实现不同类别的历史洪水的分类参数率定。Yu等[11]基于支持向量回归技术,以水文响应时间确定模型最佳输入,建立基于支持向量回归技术的洪水预报模型。
曹娥江属于钱塘江水系,是钱塘江河口段主要支流,河流长197 km,平均比降3.0‰。流域整体处于从山丘区到平原区再到河口区的特殊地理位置,上游属山溪性河流,坡陡流急,尤其是流域上游河流呈扇形分布,洪水峰高量大,下游原属潮汐河道[12-13],曹娥江河口大闸建成后成为内河,大闸调度运行受上游洪水和下游潮水双重影响,洪水传播规律复杂多变。受曹娥江潮汐影响,河床不稳定,断面变化大。虽然流域总体防洪格局已经形成,但流域洪水还未得到有效控制,因此,研究区内的汇流条件极其复杂,传统的水文水动力模型进行洪水预报通常效果不佳。为应对曹娥江中下游流域复杂的流域特性,本研究以逐步线性回归、正则化技术、L曲线方法等机器学习技术为理论基础,提出基于机器学习方法的水位预报模型,并应用于曹娥江中下游流域以检验方法的有效性。
2 数据与方法
2.1 数 据
本次研究范围为曹娥江中下游的黄泽—嵊州—上虞百官区间,嵊州和黄泽以上区间来水是中下游段主要的洪水来源,曹娥江下游左右岸的萧绍平原和虞北平原的排水以外排曹娥江为主。曹娥江流域地处浙江省东部,流域面积约6 080 km2,位置介于东经120°30′~121°15′和北纬29°08′~30°15′。本研究中采用2011—2020年东沙埠、上虞东山和百官站整编水位资料进行模型构建和验证,研究区及站网分布见图1。

图1 预报方案编制范围和主要预报断面示意图
2.2 研究方法
水文数据是典型的时间序列,不同时段观测值相互依赖,利用这种相关关系,将整个水位预报系统看作一个多输入、单输出线性动态系统,可使用通用公式表示[17]:
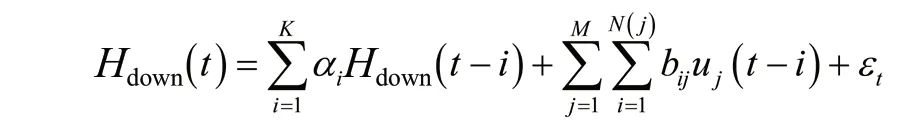
式中:Hdown(t)为系统在t时刻的输出,如t时刻的预报水位(m);uj(t-i)为第j个影响因素在t-i时刻的输入,如上游断面的水位、支流水位等(m);αi为模型参数,i= 1,2,…K;bij为模型参数,i= 1,2,…,N(j),j= 1,2,…,M,M表示有M个其他因素;εt表示随机误差项。
河道断面水位的影响因素较多,需要确定影响因素的主次及相互关系等。主成分分析概念直观、易于实现,是常用的简化影响因素的方法[14-15]。但主成分分析法转化后的各个特征维度的含义具有一定的模糊性,其物理意义通常不明确。因此,本研究使用逐步回归方法以使用最少的预测变量数来最大化预测能力。逐步回归分析是最为有效的多影响因素回归模型的建模方法之一[16],其基本思想是由少到多(或由多到少)逐个向模型中引入变量(或剔除),直到没有可以引入(剔除)的变量为止,最后通过比较在预留样本上计算出的误差进行模型的选择。逐步回归将各个自变量逐个引入(或剔除)模型,每引入(或剔除)一个解释变量后都要通过统计检验(如AIC指标)以确保每次引入新的变量之前回归方程中只包含显著性变量。
岭回归技术[17],Lasso方法[18]及ElasticNet方法(弹性网)[19]是常用的解决共线性问题的方法,3种方法的核心思想都是通过在原始目标函数上增加正则化项实现同时最小化模型残差范数和系数范数。增加的正则化项补充了额外的先验信息,要求解不能为了最小化残差平方和而强制调整系数。3种方法的主要差异可以归结为正则化项的差异,其中岭回归方法使用L2范数形式的正则化项(式):

Lasso方法使用L1范数形式的正则化项(式):

为同时获得岭回归和Lasso方法的性质,弹性网方法同时使用L1和L2正则化:

正则化参数的选择问题是一个如何平衡解的范数最小化和残差范数最小化的问题,L曲线技术通过绘制解的范数与对应残差范数的关系图来获得合适的正则化参数。L曲线垂直的部分对应着正则化参数较小的情况,此时正则化解受到较小奇异值对应扰动项的影响,而水平的部分对应着正则化参数较大时情况,此时正则化项的作用起到主导地位。在过渡区间的“拐角”附近,正则化解同时受到正则化误差和较小奇异值对应的扰动项的影响。因此,L曲线方法将曲线过渡区间的拐点(曲率最大的点)对应的正则化参数作为最优的正则化参数。
3 应用检验
对东沙埠站、上虞东山站和百官站2011年以来8~13场洪水采用机器学习的方法进行建模验证,其中东沙埠采用嵊州站、黄泽站和东沙埠站前期水位作为输入,上虞东山站采用东沙埠站和上虞东山站前期水位作为输入,百官站采用上虞东山站和百官站前期水位作为输入。分别绘制不同预报断面场次洪水洪峰水位计算值与实测值相关图,并统计各场洪水要素模拟误差,预报模型情况见表1。

表1 预报模型情况表
表2~4为东沙埠站、上虞东山站及百官站等3个预报站场次洪水模拟精度统计表。基于机器学习技术的水位预报模型均能取得较高的洪峰计算精度,且效果稳定,相关系数均接近于1,其中上虞东山站应用效果最好。
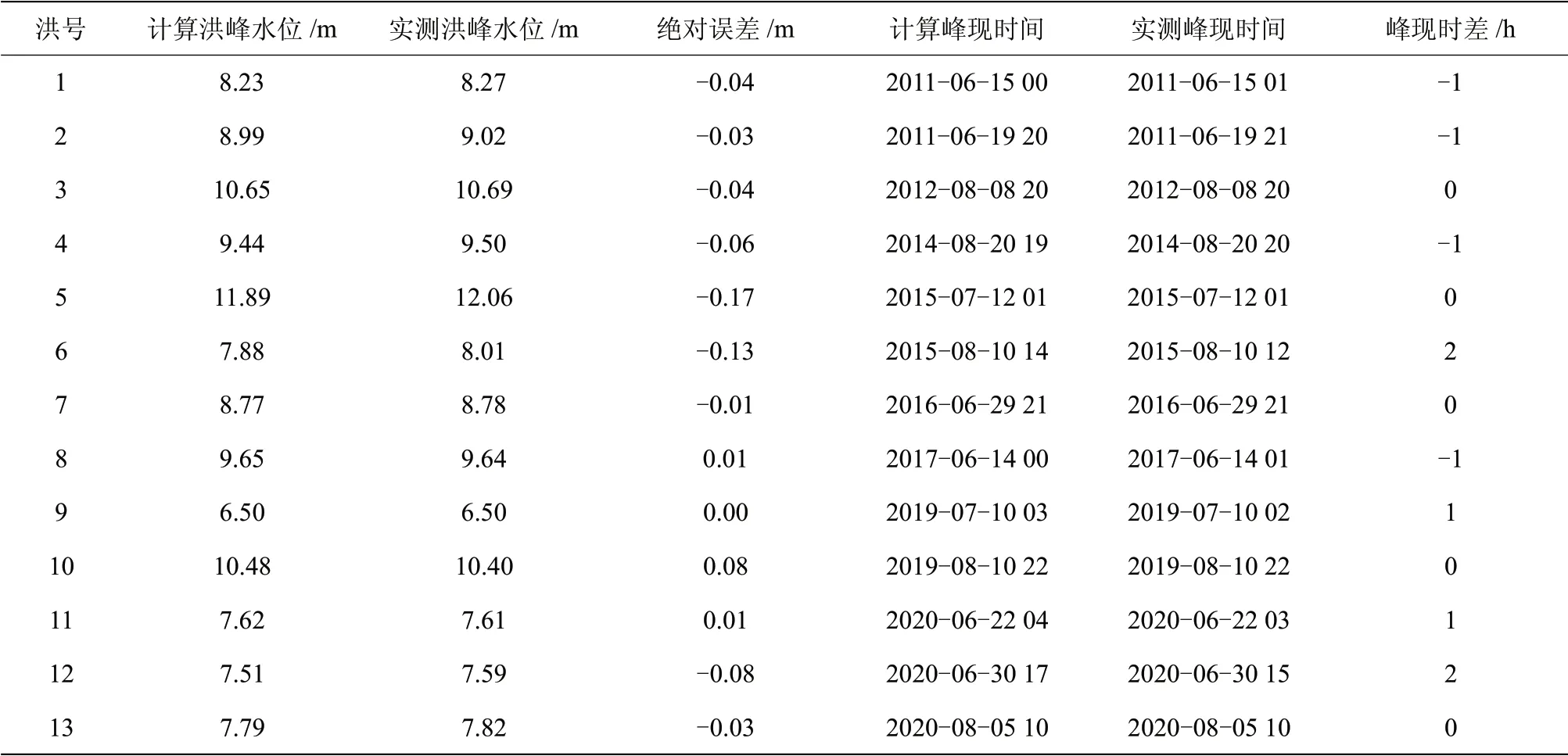
表2 东沙埠站场次洪水模拟精度统计表
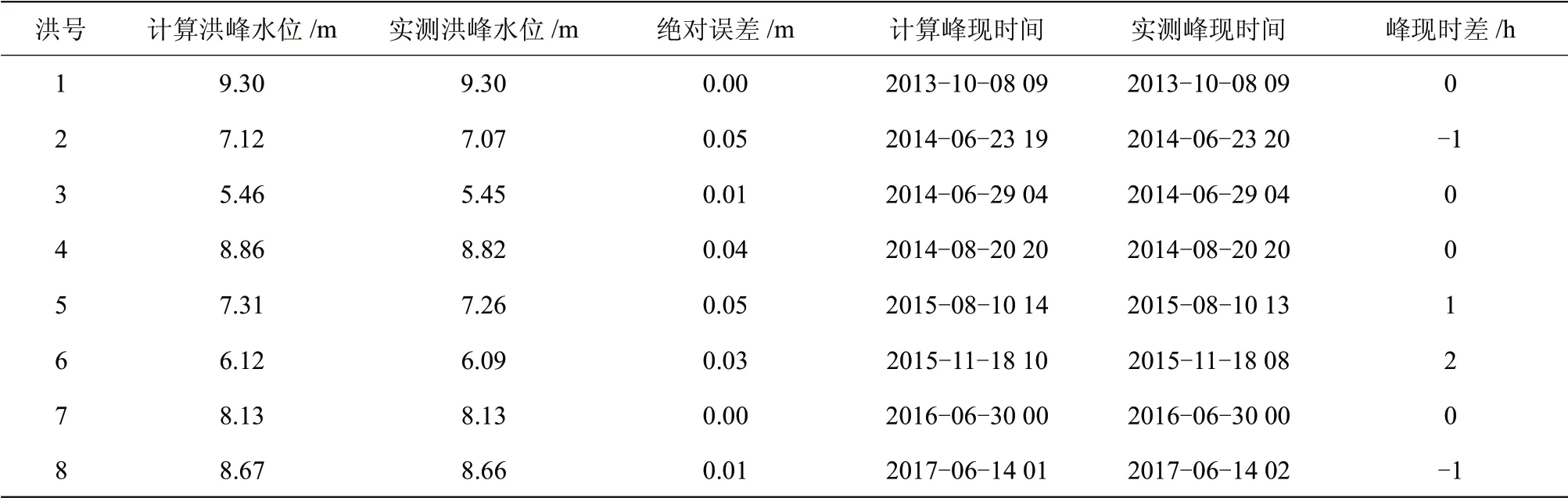
表3 上虞东山站场次洪水模拟精度统计表

表4 百官站场次洪水模拟精度统计表
根据GBT 22482—2008《水文情报预报规范》,以洪峰水位绝对误差0.10 m作为允许误差,东沙埠站、上虞东山站和百官站场次洪水模拟合格率分别为85%、100%和80%,洪峰水位模拟最大误差分别为0.17,0.15,0.27 m。东沙埠站“5号”洪水和“6号”洪水模拟洪峰水位均较实测洪峰水位偏小超过0.10 m,主要原因是建模时以嵊州站、黄泽站及东沙埠站前期水位为模型输入,当区间降雨量较大时,导致预报结果偏低。百官站“1号”洪水的计算洪峰小于实测洪峰0.27 m,主要原因是支流小舜江汤浦水库洪水期间加大出流,且区间降雨较大;“6号”洪水的计算洪峰大于实测洪峰,主要原因是受曹娥江大闸调度运用的影响。由于工程调度受人为影响较大,而基于机器学习技术的水位预报模型无法有效地捕捉和描述这一人类活动行为,导致部分场次洪水模拟精度有所降低,但总体精度稳定可靠,可满足曹娥江中下游洪水防御的需要。
4 结 论
曹娥江中下游流域的汇流条件极其复杂,使用传统的水文模型预报效果不佳。本研究实现多模型方案的对比,分析历年场次洪水特征和重点水利工程对洪水预报精度的影响,提出基于机器学习方法的水位预报模型,并在“烟花”台风中进行试运行,结果表明技术可行,方案模型准确。为流域系统内水利工程的科学提供精准预报结果,并已应用于曹娥江中下游流域,应用结果验证水位预报模型的有效性,可供防洪决策参考。此外,由于曹娥江河口大闸建成后无典型大洪水、钦寸水库建成投入运行后出库资料较少等原因,洪水场次不满足评定方案精度的要求,需继续累积资料不断完善预报模型和模型参数。

