盾构法下穿堤防开挖面支护压力研究

黄晓洪，黄 俊，俞 汇，郁高明，杨安玉

（1.新昌县水利水电局，浙江 新昌 312500；2.如皋市交通产业集团，江苏 如皋 226500；3.南通大学，江苏 南通 226000；4.水利部农村电气化研究所，浙江 杭州 310012）

1 问题的提出

极限支护压力能保证盾构的正常施工。盾构开挖面极限支护力的计算理论模型包括微观破坏分析模型、塑性极限分析理论以及楔形体理论计算模型等[1-5]。微观破坏模型认为开挖面土体颗粒相继失去稳定，并逐渐发展最终导致局部或整个开挖面破坏，主要适用于在无黏性或低黏性地层中施工的泥水平衡盾构施法，但目前针对该模型的研究还较少。许多学者利用室内试验、离心试验以及假设不同的开挖面破坏形式[6-7]，结合塑性极限理论，发展了塑性极限分析理论[8-12]。根据试验和实际工程结果，楔形体计算模型是假定开挖面为一正方形的挡土墙，开挖面前方失稳破坏土体由开挖面正前方的楔形体和其上部棱柱体两部分组成，通过楔形体受力极限平衡来求得盾构开挖面的极限支护力的一种方法。该模型简单直观，因而得到广泛应用。

盾构机磨桩过后，盾构机掘进过程的推力将全部由堤防地基承担，此时开挖面支护压力的确定至关重要，过低开挖面容易出现失稳现象，过高则对堤防造成挤压作用，不利于堤防的安全稳定性。上述基于楔形体理论推导出的公式计算相对复杂，实际使用不便。这里将河床以上堤防、水体自重荷载作用在半无限地基上，考虑地面作用的一条形分布荷载下计算地基中任意一点的附加应力，采用符拉蒙（Flamant）解答方式代替常用的半无限弹性地基自重应力计算方法，对Flamant解答积分可以确定盾构穿越堤防时地基初始水平地应力，来确定开挖面支护压力。

2 开挖面支护压力一般确定方法

当采用土压平衡掘进模式时，开挖面最佳支护压力一般由下式表示：

式中：k为主动土压力系数或者静止土压力系数，σz′为竖向有效土压力（kPa），p为水压力（kPa），20 kPa为考虑波动额外附加的支护力，可根据施工环境和设备情况控制取值。

由于开挖面稳定影响因素众多，地层条件多变，开挖面支护压力通常是依据上述经验公式进行估算，之后通过不同的支护压力控制条件下对周围地基位移检测数据反馈进行调整，并最终确定。

3 条形均布荷载作用下地基附加应力

图1为Flamant附加应力计算模型图。

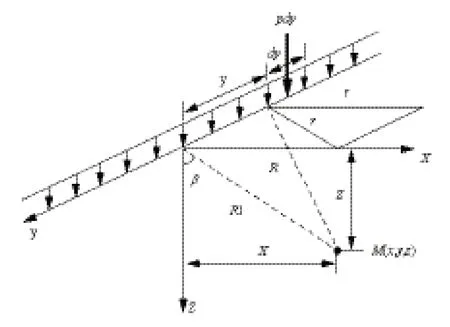
图1 竖直线荷载作用下地基中的附加应力图

半无限地基上作用一均布无限线荷载，则地基中任一点M点单元体上的竖向应力σz和水平应力σx分别为：

式中：p为竖直线荷载（kN/m）；R1为所求点M与坐标原点的距离（m），

地基中任一点的附加应力可通过对半无限地基地面的无限长条形荷载宽度的积分得到：

设条形基底宽度为b见（图2），地基表面作用有些均布基底附加应力为p。

图2 条形基底均布荷载作用下地基附加应力图

根据Flamant的附加应力解答，利用式（2）沿x轴宽度b积分，可求得地基中任意点M点竖向附加应力为：

4 盾构下穿堤防时的开挖面支护压力解析表达式推导

4.1 盾构下穿堤防时开挖面支护压力组成

图3为盾构穿越堤防示意图，相关尺寸标注为：坡比1∶n，坡宽b，坡高hc，河床水位hw，盾构机轴线中心距河床顶覆土厚度h，堤防宽度b1，河床水位宽度b2。盾构开挖面支护压力与地基初始水平应力越接近，盾构开挖对堤防的扰动就越小，因此，地基水平应力的确定便成为控制开挖面支护压力的关键。盾构开挖面支护压力一般就是地基原始水平应力，为简化计算，以盾构轴线处开挖面支护压力代替整个开挖面不均匀的支护压力。

图3 盾构穿越堤防示意图

当盾构穿越堤防区时，变化较大的覆土厚度和河面水位的变化均会对盾构开挖面支护压力的确定产生影响，因此，河床下深度为z的M点处原始竖向地应力可分成3部分：河床底面以上土体自重引起的应力；河床底面以上水体自重引起的应力；河床顶面至盾构轴线之间的土体引起的应力。

4.2 堤防荷载作用下地基附加应力的计算

图4为盾构穿越堤防的受力分析图。从图4中可看出，将河床底面以上土体及河水分别看做三角形分布荷载和矩形均布荷载，应用Flamant附加应力解答进行x方向的积分，分别解出盾构中心轴线处M点在该分部荷载下的竖向附加应力和水平附加应力，再累加隧道中心到河床上覆土自重，即可得到隧道中心线上任意一点的竖向应力和水平应力。

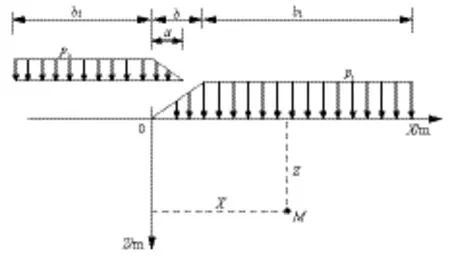
图4 堤防荷载引起的任一点的应力计算图

竖向应力和水平应力的确定过程如下：

首先，确定堤防边坡土体自重荷载和河水自重荷载作用下，盾构隧道中心轴线处M点的竖向附加应力和水平附加应力。堤防自重和水体自重荷载又可以分为二部分，分别为矩形均布荷载和三角形荷载。

堤防边坡土体自重矩形荷载作用下地基中附加应力表达式为：

水压力矩形荷载p2引起的M点竖向附加应力σz2可表示为：

堤防迎水侧堤坡土体重力三角形荷载在地基中产生的附加应力可由下式表示：

堤防迎水侧堤坡水体重力三角形荷载在地基中产生的附加应力可由下式表示：

如果堤防宽度b1较大，可按趋向于无穷远考虑，式（4）可进一步简化，即：

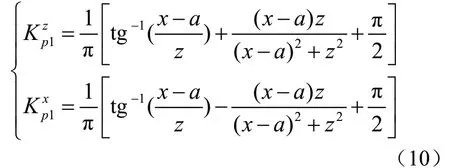
如果水体宽度b2宽度较大，可按趋向于无穷远考虑，则式（6）中竖向附加应力系数和水平向附加应力系数为：

在堤防土体重力荷载和水体重力荷载作用下，将上述4项得到堤防地基中的竖向附加应力和水平附加应力求和，即：

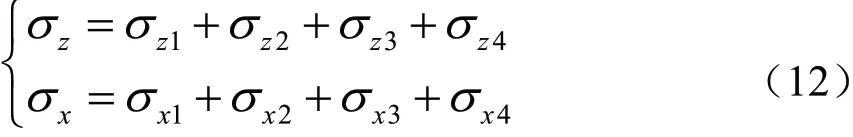
5 穿堤防时盾构开挖面支护压力计算

5.1 计算模型概述

为了减少盾构穿堤对堤防变形及稳定性的影响，通常认为与盾构掘进位置地层初始地应力一致时为最佳状态，此时对地层的扰动最小。盾构隧道直径6.2 m，隧道中心距河床的上覆土厚度10.7 m，坡比1∶3.7，土体杨氏模量3.0×104kPa，土体的侧向压力系数0.5，距离河床水位7.1 m。在此基本工况下用一般计算方法（覆土重度乘以侧压系数）与Flamant附加应力法对盾构开挖面支护压力进行计算。

5.2 结果分析

图5为支护压力计算结果图。从图5中可看出，盾构刚进入堤身时，开挖面支护压力设定在230 kPa左右，进入堤防后，支护压力逐渐降低，到堤脚时180 kPa。进入堤防后，其支护压力应略大于一般计算方法的结果；堤防边坡的存在，导致该区域内土体应力发生了明显变化，即堤脚前10～20 m地基中水平向应力明显增大，堤脚后地基中水平应力有一定幅度的降低；穿堤盾构的影响范围在坡脚前后30 m左右，意味着盾构施工在接近堤防岸坡时须加强监控，逐渐调整各项控制参数，做到信息化施工；依据一般计算方法得到堤防边坡处的附加应力变化幅度最大，Flamant应力则相对平缓，该结果能更加准确地反映盾构穿越堤防时开挖面支护压力值，更能保证工程安全实施。

图5 开挖面支护压力计算结果图

6 结 语

本文提出用于确定盾构穿堤开挖面支护压力的Flament附加应力计算模型，对开挖面支护压力进行计算，并与支护压力常规计算方法结果进行对比，计算结果表明：盾构由堤身至穿越堤防，开挖面支护压力由230 kPa左右降低至180 kPa；开挖面的支护压力应该根据覆土厚度、河床水位等条件不断动态调整；Flament附加应力计算方法得出的坡脚附近的土压力比一般方法的结果更加平稳。