轴对称凸域的包含测度

赵江甫，刘海

（1.福建江夏学院数理教研部，福建 福州 350108；2.华中师范大学国家数字化学习工程技术研究中心，湖北 武汉 430079）

设K为平面上的有界闭凸域，N为长度为l的线段，N在K内的运动测度为凸域K的包含测度。包含测度是积分几何中的重要课题之一，应用极其广泛。在统计分析中，包含测度可以对π 进行统计计算；在几何概率中，包含测度不仅可以解决探针搜索问题，而且可以为蒲丰（Buffon）投针问题及其Laplace 推广与动态推广［1］等研究提供实用快捷的工具；在积分几何中，包含测度可用于adwiger 包含问题、等周不等式的证明，还可通过运用一系列运动测度公式，解决更多几何问题。

包含测度的求解方法主要有3 种。一是由USPENSKY［2］提出的截面面积求解法。此方法计算烦琐，且线段长度受限制，较适合对称性强的简单凸域，如矩形域。二是分割法，将已知包含测度的凸域分割为新的凸域，从而求得新凸域的包含测度。如将正六边形分割为6 个全等的轴对称四边形，用正六边形域的包含测度求得四边形域的包含测度［3］。此方法计算量相对较小，适用范围亦较小。三是由任德麟［4］提出的限弦函数法，采用广义支持函数、限弦函数等给出平面凸域的包含测度一般公式。此方法更简洁，适用性更强，但未给出公式中所涉及的广义支持函数和限弦函数，求解这2 个函数是关键和难点。

已有研究采用限弦函数法解决了正六边形域、三角形域、正方形的外平行集、平行四边形域、圆域、半圆域、四分之一圆域、椭圆域、半椭圆域的包含测度问题［5-15］，但仍有很多凸域，如正五边形域、任意四边形域、任意正多边形域等的包含测度问题未得到解决，且已有研究成果大多是针对中心对称图形域的，对轴对称图形域的研究较少。基于此，本文以等腰梯形域为例，研究轴对称凸域的包含测度。虽然文献［3］采用分割法给出了等腰梯形域包含测度的计算公式，但有限制条件“等腰梯形的高不超过梯形的最短底边长”，且没有具体结果。本文尝试取消该限制条件，给出等腰梯形域包含测度的具体结果。

1 预备知识

对于轴对称凸域，可充分利用其对称性，将对称轴作为坐标轴，以减少计算量。

2 等腰梯形域的广义支持函数与最大弦长函数

3 等腰梯形域的限弦函数

图1 当θ+φ0 ＜时σM（φ）的图像Fig.1 Image of σM（φ）when θ+φ0 ＜

图2 当h ≤2b sin θ ≤≤2b 时σM（φ）的图像Fig.2 Image of σM（φ）when h ≤2b sin θ ≤≤2b

图3 当2b sin θ ≤h ≤2b ≤时σM（φ）的图像Fig.3 Image of σM（φ）when 2b sin θ ≤h ≤2b ≤

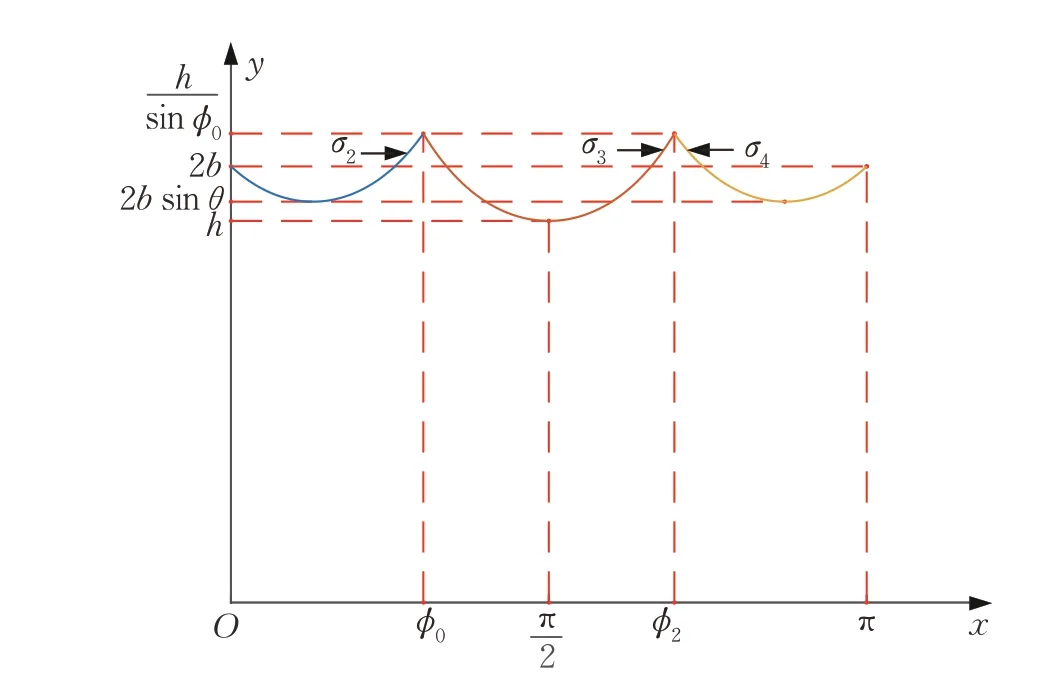
图4 当h ≤2b sin θ ≤2b ≤时σM（φ）的图像Fig.4 Image of σM（φ）when h ≤2b sin θ ≤2b ≤

图5 当2b sin θ ≤2b ≤h ≤时σM（φ）的图像Fig.5 Image of σM（φ）when 2b sin θ ≤2b ≤h ≤

4 等腰梯形域的包含测度m（l）

图6 当≥2a时p（σ，φ）的定义域示意Fig.6 Diagram of domain of p（σ，φ）when ≥2a

① 当0 ≤l＜h时，

图7 当＜2a 时p（σ，φ）的定义域示意Fig.7 Diagram of domain of p（σ，φ）when ＜2a

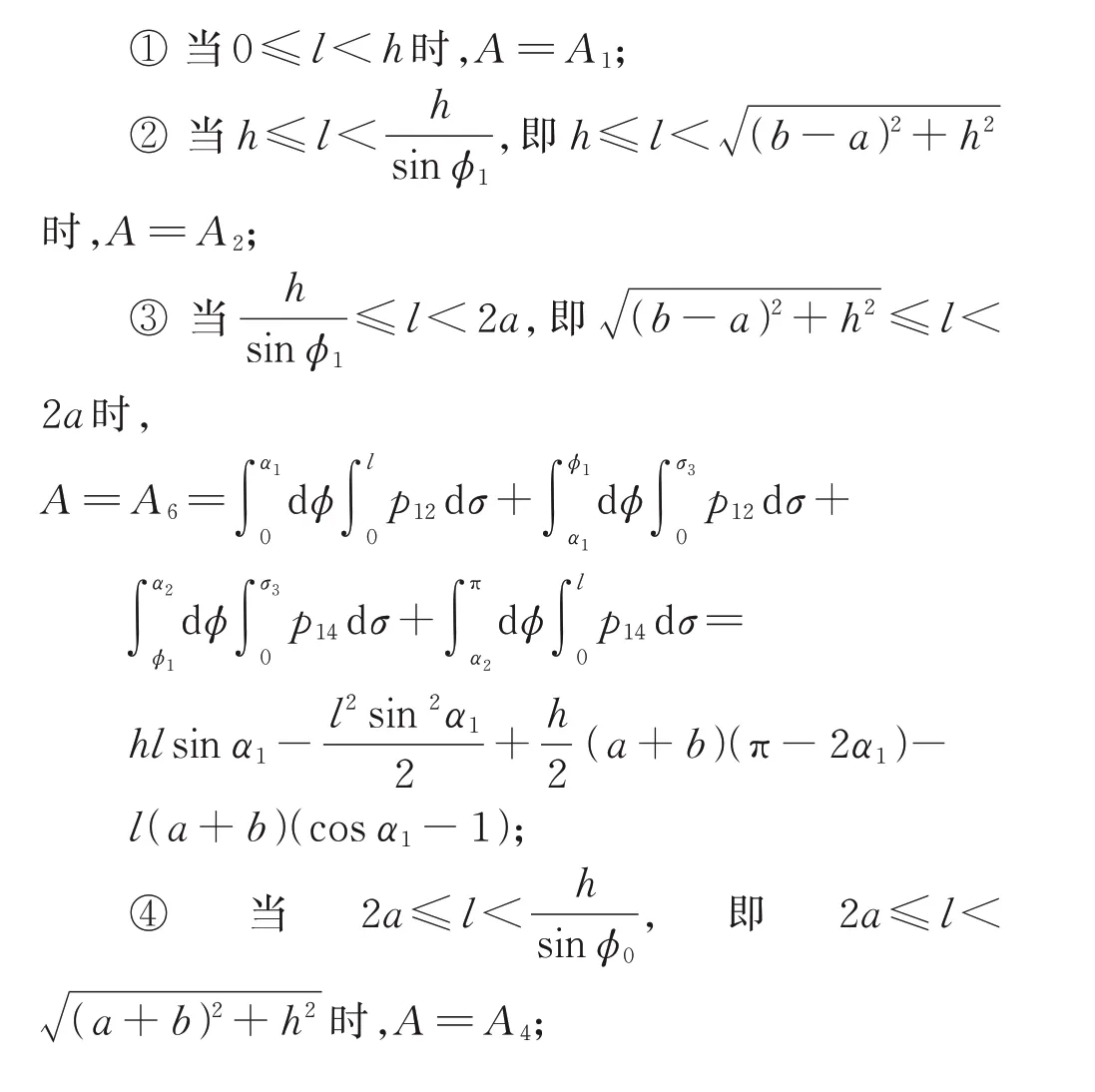
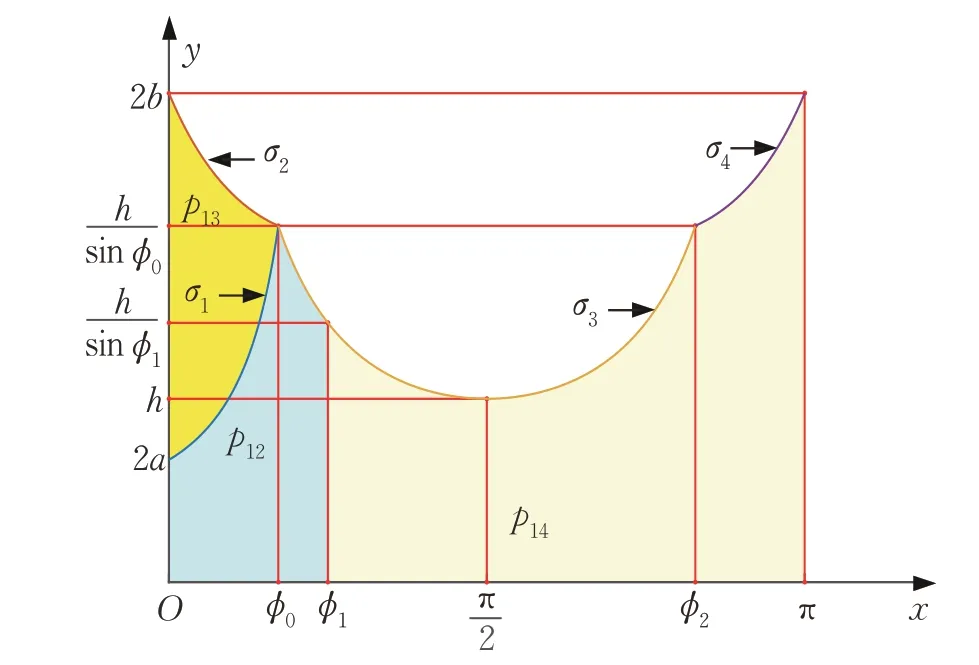
图8 当a2+h2 ≤b2，h ≥2a 时p（σ，φ）的定义域示意Fig.8 Diagram of domain of p（σ，φ）when a2+h2 ≤b2，h ≥2a

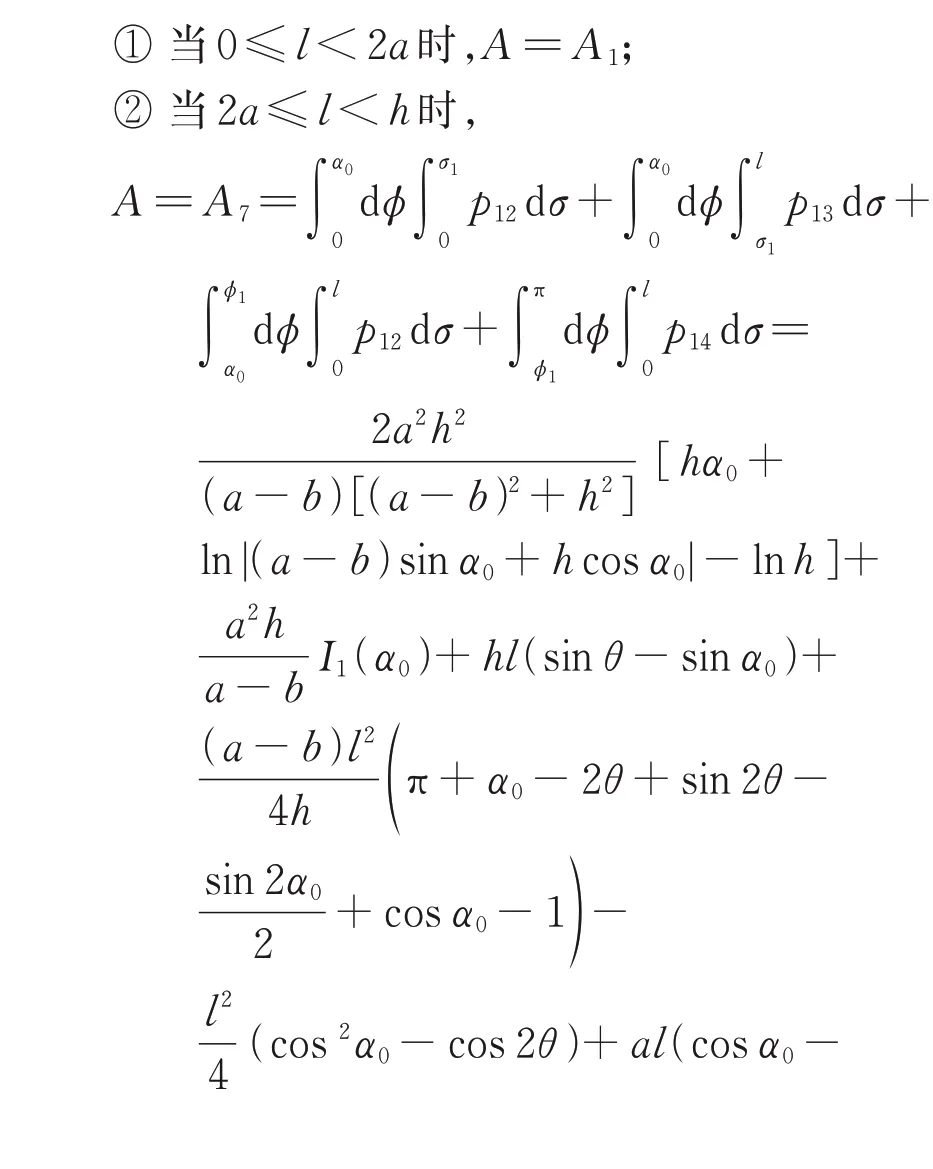
4 结 论

以等腰梯形域为例，讨论了轴对称凸域的包含测度问题，其他轴对称凸域，如正五边形域可类似讨论。给出了等腰梯形域的广义支持函数与限弦函数的求解过程，同时给出了当a2+h2≤b2时等腰梯形域的包含测度的具体结果（a2+h2＞b2时方法类似），且取消了“等腰梯形的高不超过梯形的最短底边长”这一限制条件。可利用这一结果，进一步推广Buffon 投针问题，求出小针与等腰梯形网格相遇的概率。另外，等腰梯形域的广义支持函数与限弦函数不仅可以解决包含测度问题，还可以解决等腰梯形域上的弦长分布问题，从而将应用领域推广至化学、材料学、物理等［16-18］。