Qp 上分形多孔介质的流体动力学模型

吴波

（南京财经大学应用数学学院，江苏 南京 210023）

随机多孔介质由复杂毛细网络构成，因其上的流体（如油滴，水滴及乳状液等）动力学模型在工业领域应用广泛，广受学者关注。 2016 年，KHRENNIKOV 等［1-2］提出了一种在超距空间上的数学模型框架，将液体滴流经多孔介质毛细网络的动力学主方程转化为在超距空间上的反应扩散拟微分方程。若记f(t，x)为液体滴在t时刻于毛细网中路径x被发现的概率密度，则在其上的动力学模型由以下主方程刻画：

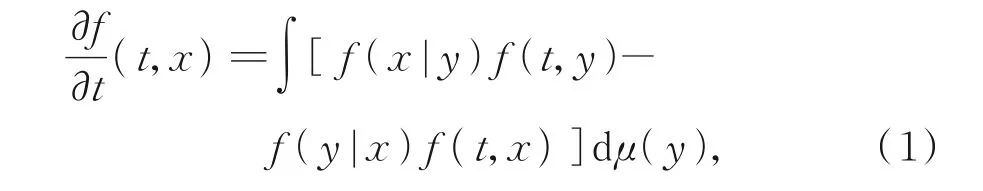
其中，μ为树形毛细网络上的概率度量，f(x|y)为液体滴从路径y到路径x的转移密度。

如考察对称形式的转移密度

式（2）右端积分部分由超距空间的拟微分算子刻画。

分形集上液体滴的流动及扩散模型在石油工业的二次采油技术设计中有重要应用［3-5］。本文的目的是将上述超距空间多孔介质的流体动力学模型推广至分形集，并用文献［6］中定义的拟微分算子Tα刻画，给出满足初始条件的液体滴在分形多孔介质上的流体动力学拟微分方程的确定解。

1 预备知识

首先，回顾p-adic 分析的一些基本知识［6-20］。

设p为素数，p的进数域为有理数域Q中的完备化Qp，并赋予p进范数|x|p，定义为

2 主要结果

3 结 论

研究了在分形集Γp，n上的一类反应扩散拟微分方程，利用苏维宜［5］定义的拟微分算子Tα，得到了该类方程的定解，并研究了该形式解的收敛性。

感谢Andrei Khrennikov 教授对本文的指导！