一种复杂场景下的路径规划问题解决方法

郭书杰，田 华，王 伟

(大连东软信息学院 智能与电子工程学院，辽宁 大连 116023)

0 引 言

路径规划是在有障碍物的环境中，按照某种评价标准寻找一条从起始点到目标点的无碰撞路径[1]。路径规划在移动机器人、电子游戏、汽车导航等多个领域均有重要的应用价值，是一个具有较高使用价值的研究方向。常用的路径规划算法有两种：基于采样的路径规划算法和基于搜索的路径规划算法。Dijstra[2]和A*算法[3]是典型的基于搜索的路径规划算法。这类算法是完备的和最优的。由于要使用较小的步长遍历规划空间，其规划效率相对较低。典型的基于采样的路径规划算法有PRM[4]、 RRT[5]和EST[6]等。 这类算法使用随机采样的方式探索规划空间，所以具有比基于搜索的路径规划更高的效率。基于采样的规划方式有一定的随机性，仅仅是概率完备的，而且不是最优的。为了进一步提高算法的搜索效率，JJK Jr和Steven M. LaValle提出了一种改进算法RRT-connect[7]。RRT-connect能够提高RRT算法的效率，不过它仍然不是最优的，甚至不是渐近最优的。为了提高规划路径的质量，出现了一些改进算法，如RRT*、PRM*[8]、LBT-RRT[9]。这类改进算法能够达到渐近最优。还有一个改进方向是将基于搜索的相关技术引入到基于采样的规划中来，结合基于采样的规划算法和基于搜索的规划算法的优势，兼顾了效率和路径质量，如HRRT[10]、Anytime RRT[11]、Bi-RRT*[12]、C-FOREST[13]、Informed RRT*[14]等。这类算法在一定程度上提高了算法的收敛速度，但由于它们均是基于RRT的改进算法，所以仍然难以保证规划出来的路径质量的最优性。为了进一步提高路径质量，出现了BIT*、AIT*和ABIT*[15-16]等算法，通过引入节点排序和边排序，在限定的子集中执行排序搜索，从而达到提高路径质量的目的。还有其他A*算法的改进算法[17-18]和基于智能优化算法的路径规划算法[19]。

实验发现，尽管这些改进算法在一定程度上提高了规划效率和路径质量，但在限制较多的空间中，特别是在窄通道场景和Z字形场景中，它们的规划效率会急剧降低，难以在有限的时间内规划出一条路径来。为了解决复杂场景下的路径规划问题，提出了一种相对高效的关键点路径规划算法(key point path planning，KPP)，该算法在提高路径优化效率的同时，也优化了规划出来的路径的质量，较好地解决了特殊环境下的路径规划问题。实验结果表明，KPP不仅能够高效地完成窄通道场景和Z字形场景中的路径规划，在其他常见场景的应用中也有不俗的表现。

1 路径规划问题

路径规划就是在给定空间中，规划出一条从起始点到目标点的无碰撞路径，使得该路径的代价尽可能小。记空间X⊂Rn为P，Xobs表示P上被障碍物占据的空间；Xfree=XXobs表示P上可以通行的空间；Dstart表示起始点；Dgoal表示目标点；σ：[0,1]X表示连接Dstart和Dgoal之间的路径；∑表示Dstart和Dgoal之间所有的路径组成的集合；S：∑R表示一条路径的代价函数；则路径规划问题可以描述为：

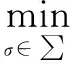
Dgoal, ∀t∈[0,1],σ(1)∈Xfree}

2 关键点路径规划算法

关键点路径规划算法基于“两点之间直线最短”的原理，首先找出阻碍起始点与目标点直线连通的障碍物KObses；然后找出绕过KObses的最近路线必须经过的点作为关键点；接着以这些关键点为引导，将路径规划从随机搜索转换为启发式搜索，从而提高规划效率和路径质量；最后通过路径压缩来减少路径长短，进一步提高规划出的路径的质量。

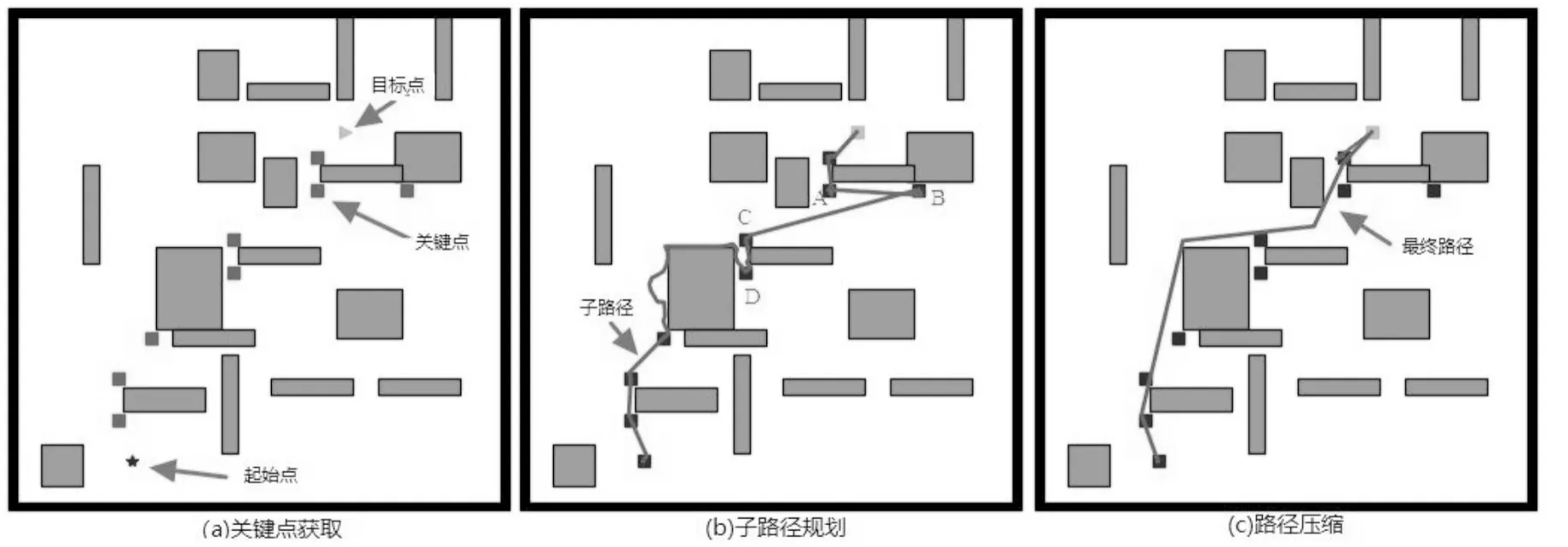
图1 KPP处理过程

关键点路径规划算法的处理过程如图1所示。第一步：找出起始点到目标点之间的关键点(见图1(a))。这些关键点是通过对起始点和目标点连线上的障碍物的某些顶点外推得到的。第二步：选用某种路径规划算法规划出各个关键点之间的子路径；再以关键点为连接点，将这些子路径连接在一起，形成起始点到目标点间的初始路径。第三步：对第二步中得到的初始路径进行压缩，删除其中的冗余路径段，得到最终路径(见图1(c))。

2.1 获取关键点

关键点是指绕过某一障碍物的最短路径上，与该障碍物的距离小于某一设定阈值的点。假设障碍物Obsi的外边界为boundryi，从起始点到目标点的路径中，一条绕过Obsi的最短路径为pathi，则称集合{pointi|pointi∈Xfree∧pointi∈pathi∧distance(pointi,boundryi<ε}中的点为关键点。这些关键点是距离障碍物较近的可通行节点，所以经过关键点的路径是绕过某障碍物的近似最优路线。关键点的获取要经过两步完成，第一步是获取所有潜在关键点，第二步是从潜在关键点中选出相对较好的点作为最终的关键点。

2.1.1 获取潜在关键点

为了便于讨论，该文以实际障碍物的正外接矩形来代表障碍物本身，文中的障碍物均指实际障碍物的正外接矩形。在寻找可能的关键点时，首先找到所有与起始点和目标点的连线相交的障碍物。然后对这些障碍物的四个顶点分别向远离中心点的方向外推，如对左上点进行左推和上推，对右下点进行右推和下推。通过这种外推得到的点就是可能的关键点。左上点的外推过程如下：首先完成对左上点A的左推，即以步长step向左寻找障碍物的左侧边界，若在地图边界内找到了该障碍物的左侧边界则把当前点拉回到障碍物内，并以步长step向上寻找障碍物的上侧边界；若在地图边界内找到了该障碍物的上侧边界，则对该点进行一步左推，并返回左推后的点，即A的外推点。具体过程如图2所示。障碍物的其他顶点的外推过程与此类似，不再赘述。需要说明的是，为了便于后续操作，起始点和目标点也分别被视为可能的关键点。

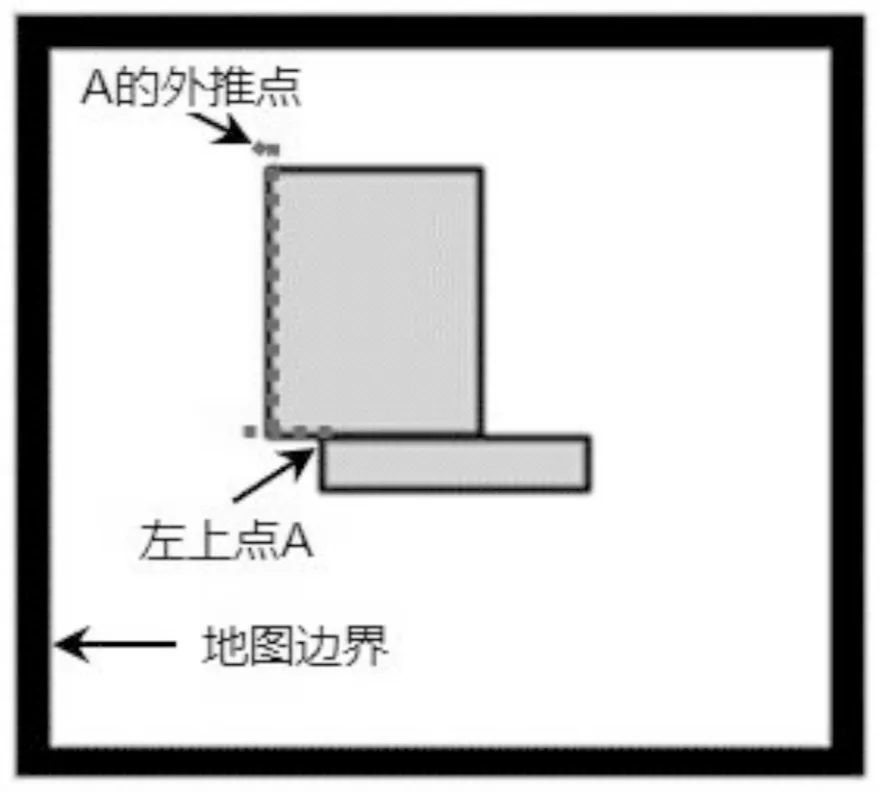
图2 左上点的外推过程

2.1.2 关键点选择

在一次路径规划中，可能的关键点数量较多，其中有一些点能够在路径规划过程中起到正向的启发作用，也就是说经过这些关键点的路径代价会比较小，另一些则不能。关键点选择的目的就是从可能的关键点中，选出那些具有正向启发作用的点作为最终的关键点。

在进行关键点选择时，从起始点开始，在可能的关键点组成的集合SP中查找距离最近的无碰撞连接点p，若找到则将p加入到关键点集合SKP中，并将p点从SP中删除，然后从p开始在SP中继续查找距离最近的无碰撞连接点。重复上述过程，直至找不到无碰撞连接点或找到的点是目标点。如果目标点不在SKP中，则从目标点开始，在SP中查找距离最近的无碰撞连接点p，若找到则将p加入到关键点集合SKP中，并将p点从SP中删除，然后从p开始在SP中查找距离最近的无碰撞连接点。重复上述过程，直至找不到无碰撞连接点或找到的点已经存在于SKP中。简单来说，关键点选择的过程，就是分别从起始点和目标点开始，在SP中查找最近的可以无碰撞连接的点的过程。

2.2 实施路径规划

通过关键点的选择，得到了一个起始点到目标点之间的关键点数组。数组中相邻两个关键点之间的路径称为子路径。接下来根据需要选用某种路径规划算法完成子路径的规划。最后以关键点为连接点，将这些子路径连接在一起，形成初步路径。由于难以找到适合于任何情况的最优关键点选择策略，所以选出的关键点并不都是对路径规划具有正向的启发作用，如图1(b)中的关键点B；同时，因为所选择的路径规划算法不一定是最优算法，甚至可能不是渐近最优的算法，所以初步规划出来的路径通常不是最短路径。为了解决这一问题，需要对初始路径做进一步优化，也就是路径压缩。

路径规划的具体过程如下：假设经过关键点的生成与选择后，得到了关键点数组arrayKeypoint。对于arrayKeypoint中的每一个点arrayKeypoint[i]，使用选定的路径规划算法，规划以arrayKeypoint[i]和arrayKeypoint[i+1]为起始点和目标点的路径，得到子路径subPath_i，并将subPath_i加入到初始路径Path中。最后对Path进行压缩，以提高路径的质量。路径压缩是为了减少路径长度，提高路径质量，其实质就是删除一条路径中的冗余路径点。冗余路径点的定义如下：

冗余路径点：对于一条路径Path上的一段子路径sPath，令sPath的起止点分别是PointStart和PointEnd，如果由PointStart和PointEnd两个点构成的子路径也是无碰撞的可行路径，则称sPath上除起止点之外的其他路径点为冗余路径点。

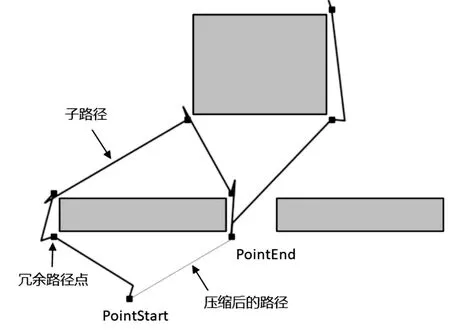
图3 冗余路径点

如图3所示，因为由PointStart和PointEnd两点构成的路径是无碰撞的可行路径，所以以PointStart和PointEnd为起止点的子路径sPath上的其他点均为冗余路径点，子路径sPath就可以被压缩成compressed path，由此来降低路径长度。路径压缩从路径的目标点开始，逐一查找距离当前点curr_point最远的无障碍连接点farthest_collision_free_point，并删除curr_point与farthest_collision_free_point之间的冗余路径点。路径压缩算法首先将目标点赋值给当前点curr_point，并将curr_point加入到压缩后的路径中；然后查找路径中距离当前点最远的无碰撞点farthest_collision_free_point，并将该点加入到压缩后的路径中；最后以farthest_collision_free_point为当前点，继续寻找。循环执行上述过程，直到找到的最远无碰撞点为起始点。

2.3 算法的总流程

关键点路径规划算法首先获取可能的关键点，潜在关键点的获取是通过对起始点与目标点连线上的障碍物的顶点进行外推实现的。然后进行关键点选择，依据步长最小且可连通为原则，在可能的关键点中选出路径规划所需的关键点。接下来进行初步的路径规划，选用某种路径规划算法在两个相邻的关键点之间规划子路径，并将这些子路径合并成总路径。最后进行路径压缩，采用删除总路径中的冗余路径点的方式，对原始路径进行优化，得到最终路径。

2.4 算法分析

关键点路径规划算法的优点是效率较高，规划的路径质量也较好。与其他路径规划算法相比，关键点路径规划算法多了两个步骤，一个是关键点的获取，另一个是路径压缩。通过关键点获取，算法找到了绕过从起始点到目标点之间的障碍物的关键点，并使用这些关键点来引导路径规划算法完成规划。这些关键点将一条未知路径分割成多条子路径。通过分割将规划空间切分成更小的子空间，从而减小了问题规模，提高了规划效率。另一方面，由于大多数关键点之间是可以无障碍连通的，所以这些子路径的规划就变得非常简单，只要将两个关键点连接起来就行了，路径规划的效率得到了较大的提高。同时，关键点的引入将随机搜索转换为启发式搜索，能够使算法朝着目标点的方向进行搜索，所以算法规划出了更短的路径。尽管关键点的引入极大地提高了算法的效率和路径的质量，然而，由于地图环境复杂多样，起始点和目标点的位置又不确定，导致难以找到一个最优的关键点选择策略，障碍物的一个顶点在某种情况下是最优路径经过的点，在另外一种情况下又不是了。所以照固定的关键点选择策略选出的关键点中，会出现少量坏点，这些坏点降低了路径的质量。另外用于完成关键点间路径规划的算法不一定是最优算法，规划出来的子路径也可能会出现较多的冗余路径点。对此，路径压缩很好地解决了这两个问题。路径压缩能够以较高的效率找出路径中的冗余部分，并将其删除，从而提高最终路径的质量。所以通过关键点和路径压缩两个操作，可以提高路径规划的效率和路径的质量，特别是在狭窄通道环境和“Z”字形通道环境下。

关键点路径规划算法的缺点是需要进行频繁的碰撞检测。在进行关键点获取和路径压缩时，都需要多次进行碰撞检测。当地图上障碍物数量过多时，会在一定程度上影响规划效率。

3 实 验

为了验证关键点路径规划算法的性能，进行了多组对比实验。实验中选用RRT-connect完成关键点之间的路径规划。

3.1 与RRT-connect算法的对比实验

3.1.1 实验过程

实验模拟了四种场景(scenario)，如图4所示。分别是离散障碍物场景、窄通道场景、Z字形场景和迷宫场景。实验中选用规划效率和规划出来的路径质量作为评价算法优劣的标准。每个场景选择五组典型的起始点和目标点进行路径规划，图4中的S[i]表示第i组的起始点，G[i]表示第i组的目标点。每组运行50次，记录每次运行的时间和路径长度。通过比较平均运行时间和平均路径长度来对比算法的规划效率和规划出来的路径质量。实验中RRT-connect算法的迭代次数设置为50 000。

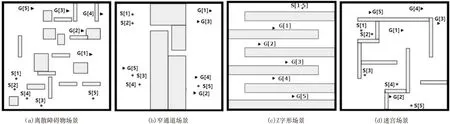
图4 四种场景

3.1.2 实验结果

离散障碍物场景实验的结果如图5所示。图5(a)是路径规划所用时间的对比图，其纵坐标是规划路径所用的平均时长，单位为毫秒；横坐标是路径起止点的组序，如横坐标的“1”就表示规划的是以图4(a)中的S[1]为起始点、G[1]为目标点的路径；图例中的KPP代表关键点路径规划算法的运行结果，RRT-C是RRT-connect算法的运行结果。图5(b)是规划出来的路径长度对比图，其纵坐标表示算法规划出来的平均路径长度，横坐标及图例所表示的意义与图5(a)相同。如无特殊说明，后续实验结果图中各元素的意义均与图5相同，不再赘述。

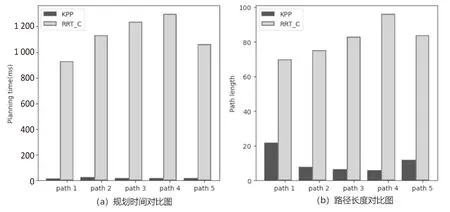
图5 离散障碍物场景实验结果

由图5不难看出，在对图4(a)中的5组路径规划中，KPP算法在规划效率和路径质量方面都比RRT-connect算法好很多。KPP算法的平均耗时仅占RRT-connect算法的1.66%，KPP算法规划的平均路径长度仅占RRT-connect算法的13.22%。

窄通道场景的实验结果如图6所示。在窄通道场景下，KPP算法在效率方面的提高更加明显，KPP算法的平均耗时仅占RRT-connect算法的0.16%。KPP算法规划的平均路径长度占RRT-connect算法的21.67%。这一比例有所升高，其原因是窄通道限定了路径的大致方向。不管哪种算法规划的路径，都要从窄通道中通过，而该通道的长度是固定的，所以在通道内部，这些路径的长度差就被限定在一个较小的范围内了。

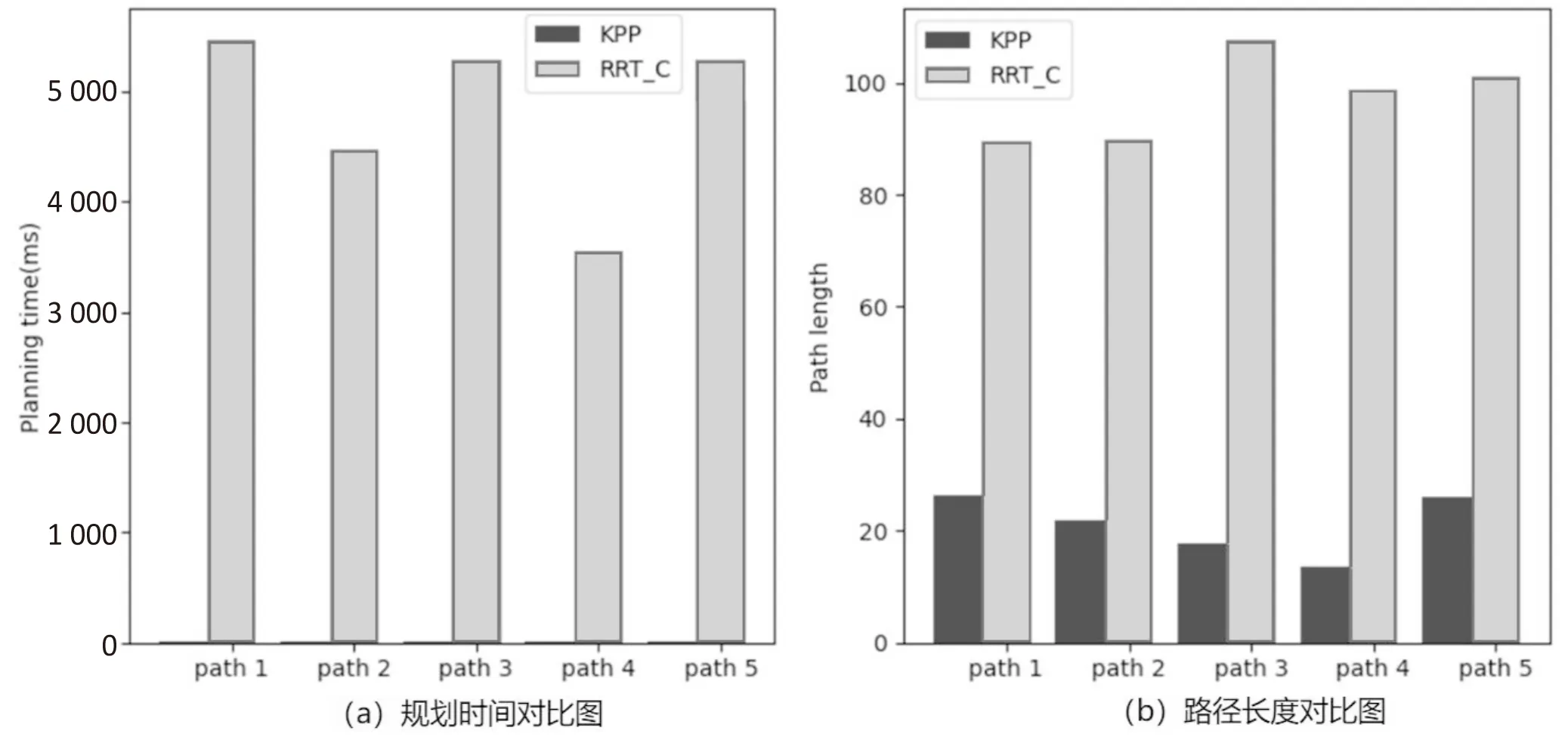
图6 窄通道场景实验结果

Z字形场景的实验结果如图7所示。在Z字形场景实验中，图4(c)中的5组起止点中，RRT-connect算法仅成功规划出了两组，分别是起止点相距较近的S[1]到G[1]的路径和S[2]到G[2]的路径。这两组路径规划过程中，KPP算法的平均耗时仅占RRT-connect算法的0.09%；KPP算法规划的平均路径长度占RRT-connect算法的23.18%。与窄通道相比，Z字形通路更多地限制了路径的走向，所以Z字形场景中，KPP算法规划的平均路径长度与RRT-connect算法规划的平均路径长度进一步提高。

迷宫场景的实验结果如图8所示。KPP算法的平均耗时仅占RRT-connect算法的0.08%；KPP算法规划的平均路径长度占RRT-connect算法的12.32%。

由实验结果可以看出，在四种不同的场景中，KPP算法的规划效率和规划出来的路径长度均比RRT-connect算法好很多。特别是在窄通道场景和Z字形场景中，当以高效著称的RRT-connect算法都难以成功规划处路线时，KPP仍然可以在较短时间内规划出一条质量较高的路径。

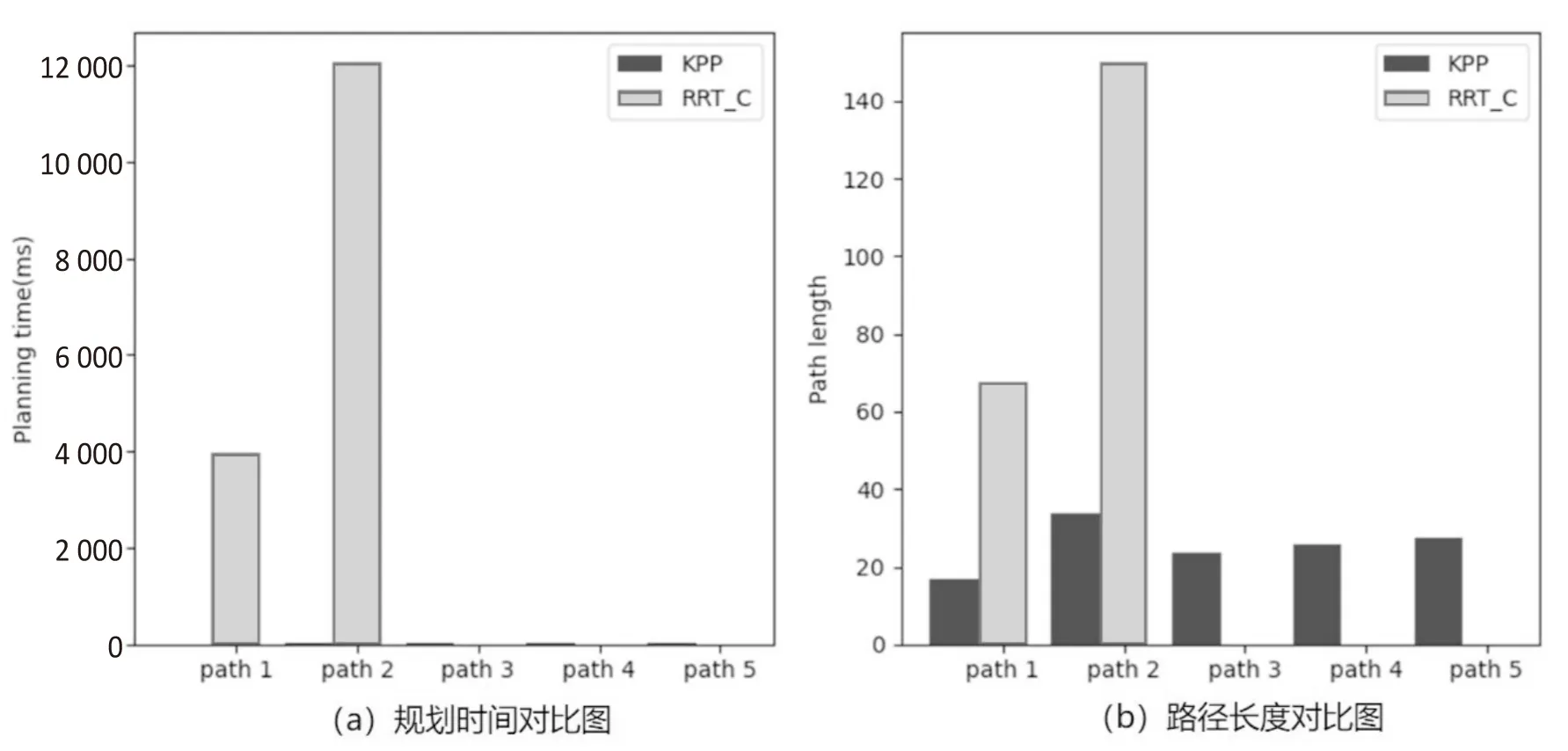
图7 Z字形场景实验结果

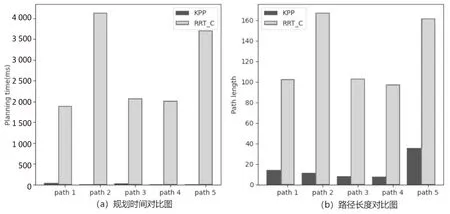
图8 迷宫场景实验结果

3.2 与BIT*算法的对比实验

为了进一步检验KPP算法的性能，与BIT*算法做了对比实验，实验选用了3组起止点。每组起止点完成50次规划，通过对比平均规划用时和平均路径长度来评价算法性能。

实验结果如下：进行第一组路径规划时，BIT*算法的平均耗时为27 343.75毫秒，平均路径长度为26.976 321；KPP算法的平均耗时为0.27毫秒，平均路径长度为26.131 984。进行第二组路径规划时，BIT*算法的平均耗时为25 312.5毫秒，平均路径长度为23.484 871；KPP算法的平均耗时为0.21毫秒，平均路径长度为23.332 335。进行第三组路径规划时，BIT*算法的平均耗时为29 484.375毫秒，平均路径长度为33.495 748；KPP算法的平均耗时为15.625毫秒，平均路径长度为34.640 041。三组路径规划中，KPP算法平均耗时明显要小于BIT*算法；在路径长度方面，除第三组外，KPP规划的路径长度均略小于BIT*算法规划的路径长度。在第三组路径规划时，由于关键点选择时，以最小步长为原则，选取距离最近的节点，所选节点并不是最好的，从而导致KPP算法所规划的路径略长。

4 结束语

KPP算法通过引入关键点，将较复杂的长路径规划转化为规模较小的子路径规划；同时将随机搜索转化为启发式搜索，所以其规划效率较高，特别是在窄通道、Z字形或障碍物较密集的场景中，当其他算法无法成功规划路径时，KPP算法仍然可以较快地完成规划。同时，路径压缩的操作也减少了KPP算法规划出来的路径长度。尽管KPP算法是用于解决2D问题路径规划问题的，可以很容易地将其扩展到立体空间中，求解3D问题路径规划的问题。

由于选出的关键点不一定是最合理的，部分关键点可能会给规划带来错误的引导，进而导致KPP规划出来的路径质量降低，所以KPP算法不是最优的。