比例伺服阀低液动力阀芯导流结构优化设计*

张志豪，苏 琦，李海宾，方梓帆，陈冬冬，魏远恒

(1.浙江大学 机械工程学院·杭州·310057；2.上海衡拓液压控制技术有限公司·上海·201612；3.内蒙古北方重工业集团有限公司·包头·014033)

0 引 言

液压传动比电气传动、机械传动等驱动力更大、稳定性更好、体积紧凑。液压阀是液压系统的核心控制元件，用于控制液流的流动方向、压力和流量等，特别在高性能比例伺服阀液压控制系统中，比例伺服阀的控制性能直接影响着液压系统的性能。流体的流态在经过阀口后会发生改变，对阀芯产生液动力，液动力属于干扰力，具有很强的随机性和不稳定性，其作为比例伺服阀阀芯控制系统中最大的干扰力，限制了比例伺服阀的静动态控制性能。对阀芯处的液动力进行研究可以有效减少其对液压阀性能的不利影响，进而指导比例伺服阀产品设计和工程实践应用。

目前，国内外众多学者已针对液压阀的液动力开展了大量研究，计算流体力学(Computational Fluid Dynamics，CFD)方法的发展使得这项研究更加深入。浙江大学谢海波等基于CFD仿真方法研究了不同的阀口形态对锥阀液动力的影响规律，分析了阀座上有无倒角时阀芯所受液动力的情况，对液动力补偿优化设计具有重要的指导意义；王迪等提出了带孔阻尼套结构，通过改变阀芯表面压力分布和油液射流角，以降低开关阀的阀芯液动力；杨庆俊等针对入口节流型滑阀开展了仿真试验，计算了不同结构参数和工作条件下液动力的变化规律，并分析了其内在机理；大连理工大学张宏等对多路阀不同开度和流量下的阀芯受力情况进行了数值模拟分析,并通过试验验证了仿真的正确性。

比例伺服阀在现代工业中应用广泛，其执行元件主要为滑阀式结构，即阀芯、阀套、阀体结构。滑阀通过阀芯与阀套间的相对运动，改变节流口面积，控制流量大小。在比例伺服阀中，液动力是最主要的外部干扰力，会因阀口开度的大小和阀芯结构的不同发生变化。对伺服阀滑阀内部进行流场分析有助于深入了解其工作机理，对液压阀结构优化设计和提升控制性能具有重要意义。J.R.Valdes等基于动量定理和流体不可压缩理论体系，针对比例阀的稳态液动力和流量建立了可估算的数学模型；杨科等采用Fluent中的动网格技术，研究了伺服阀滑阀在小开度范围内的流量和液动力特性；陆倩倩等则对出口节流型换向阀的径向液动力开展了系列研究，但多数学者认为液压阀结构对称时，径向液动力是自相平衡的。

本文针对一种比例伺服阀，开展阀芯导流结构创新设计，提出优化设计方案，采用CFD技术对阀口处的流体域进行数值模拟分析，以研究不同的阀芯导流结构下的液动力特性。

1 方案设计

1.1 计算理论

稳态液动力又称伯努利力，是液流进出阀腔后改变方向给阀芯的反作用力，直接影响滑阀的工作性能和控制性能。

稳态液动力的基本计算公式为

=cos

(1)

式中，为油液密度；为流量；为流速；为流束射流角。

本文研究的滑阀主阀芯径向存在对称的4组节流口，每组节流口周向均匀分布4个相同的阀口，因此阀芯径向力处于平衡状态，稳态液动力作用于阀芯轴线方向的壁面上。绘制滑阀阀口处的结构简图，受力面包括阀芯轴向壁面、左右壁面、阀套内壁面以及节流口壁面，如图1所示。根据动量定理，对阀芯液动力进行理论计算，其动量公式为

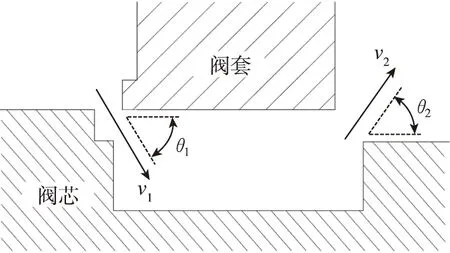
图1 滑阀的稳态液动力分析模型Fig.1 Steady-state hydrodynamic analysis model of slide valve

=-(cos-cos)

(2)

式中，、分别为流入、流出速度；、分别为进出口的射流角。可知，阀芯所受液动力受进出口射流角的影响。

1.2 液动力补偿方案

为减小液动力对液压阀性能的影响，现有多种液动力补偿方案，经典的方法如阀套运动法、射流导向法以及压降补偿法等。射流导向法通过优化进口角度、阀套长度等参数，降低液动力；压降补偿法通过增加节流孔处的压降，使之作用在阀芯上以补偿稳态液动力，但只适用于大流量系统。由于比例伺服阀种类繁多，其液动力补偿方案也因工况的复杂性和阀口形状的特殊性而制定。

阀芯和阀套的结构会直接影响射流角的大小，因此，理论上适量改变阀芯导流内壁的弧度，可调整阀芯所受液动力的大小。根据1.1节的理论分析，本研究主要针对阀口导流壁面提出创新设计方案。

图2所示分别为阀芯导流内壁的传统结构和创新后的结构图。由图2可见，传统方案中进油口处的阀芯纵向内壁与轴向内壁垂直，仅有较小的圆角；而创新方案中改变了纵向内壁的方向，整体的导流内壁呈圆弧过渡状。从图2可观测到，创新设计后的射流角比传统方案的射流角数值要小，代入式(2)可得出，在小开度范围内创新设计方案的液动力理论值小于传统方案。

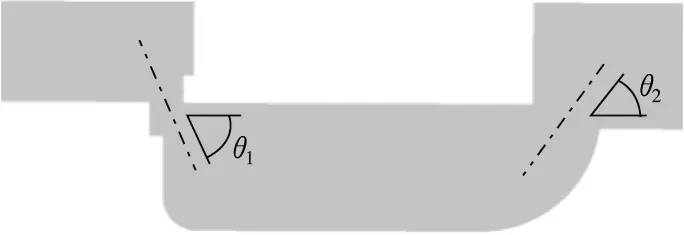
(a)传统方案

1.3 方案设计与模型建立

基于上述创新方案对本研究的比例伺服阀阀芯导流内壁进行创新设计。

首先运用SolidWorks软件建立滑阀主阀芯、阀套、阀体的三维几何模型，如图3所示，主阀芯从左到右沿轴向分布4组节流口，分别对应A-T、P-A、P-B、B-T节流口，每组节流口又包含周向分布的4个阀口。滑阀模型建好后，内部生成流体域，直观展示油液的流动情况，如图4所示。

图3 阀腔三维模型Fig.3 Three-dimensional model of valve chamber

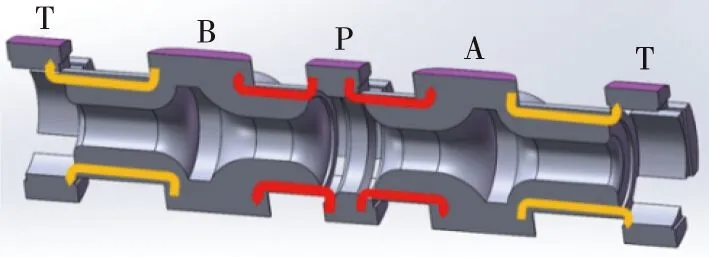
图4 流体域模型Fig.4 Fluid domain model

该滑阀结构上存在较好的对称性，即无论主阀处于左位还是右位，都有2个阀口处于节流状态，如左位状态时油液流向为：P→A、B→T，每个阀口处实际上由上下前后4个相同的阀口组成，且所有阀口的尺寸都一致。为减小计算量，缩短运算时间，初步选择左位状态下单个阀口及其连通容腔中的油液为分析对象，将单阀口的流量和液动力数值乘以阀口数量作为总流量和总液动力。

对P-A、B-T这4个阀口的阀芯导流内壁分别进行创新设计，传统方案为两垂直壁面，拐角处设置较小的圆角；创新方案则设计为圆弧状导流壁面，圆弧均与阀芯轴向壁面相切，设计参数如表1所示。绘制各个阀口的传统结构和创新结构对比图，如图5所示，其中4个阀口的传统结构分别用P、A、B、T表示，创新结构分别用P、A、B、T表示。

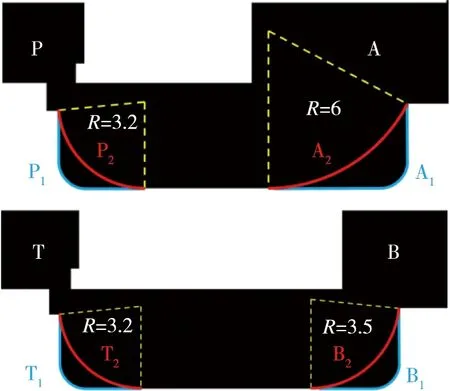
图5 传统方案与创新方案的结构参数对比图Fig.5 Structure comparison chart of traditional and innovative schemes

表1 阀芯导流壁面设计参数Tab.1 Design parameters of valve guide wall

对每个阀口均做结构创新设计，则P-A阀口有PA、PA、PA、PA四种结合方案，同理B-T阀口有BT、BT、BT、BT四种结合方案，再将阀口两两结合最终形成共十六种总方案。接下来进行仿真实验，探究各个方案对流场状态及阀芯所受液动力的影响规律。

2 仿真设置

2.1 网格划分与Fluent仿真设置

本研究中主要探讨最大开度小于1mm的开口滑阀在不同开度下的阀芯液动力特性和液流状态。使用传统的仿真分析方法只能不断改变模型的开度尺寸，效率低下；而运用CFD滑移网格法则更加高效便捷。其原理是采用瞬态分析思路，设置阀芯移动速度，在每个时间步长内，将阀芯油腔移动一小段距离进行计算，可得到从0开度到最大开度下的流量和液动力数据。在Fluent中对阀口的特殊形状作网格细化处理，建立的仿真模型更加精确，更贴合实际工况。

利用ANSYS Fluent软件进行仿真分析，假设流体域介质为不可压缩的牛顿流体，忽略重力和阀腔内部的传热影响。采用Mesh工具对流体域进行网格划分，模型如图6所示，该模型节点数为31万，网格数为53万，网格比较精细，仿真分析精度较高。

图6 单个节流口(P-A)网格模型Fig.6 Single orifice (P-A)grid model

仿真参数设置主要包括边界条件、介质参数以及求解原理等，如表2所示。

表2 流场仿真主要参数设置Tab.2 Main parameter settings of flow field simulation

2.2 网格无关性验证

网格无关性即网格的疏密程度及数量不影响数值计算的结果。由于滑阀阀口处的结构较为复杂，在Fluent仿真过程中,网格划分质量会直接影响仿真结果，因此需要验证仿真试验的网格无关性。取P-A模型进行网格无关性验证，得到验证曲线如图7所示。可见网格数量为53万和86万时的仿真结果差异较小，故而判断53万网格数量的仿真模型和结果具有普适性和可靠性。

图7 模型(T-B)网格无关性验证曲线Fig.7 Model (T-B)grid independence verification curve

3 仿真结果分析

3.1 流态分析

最终获得不同结构方案的仿真结果，如图8所示，其中前4组图片分别为P-A阀口的压力和流速对比云图，后4组图片分别为B-T阀口的压力和流速对比云图。

整体上可以明显观察到，有圆弧导流壁面时的压力场分布情况比垂直壁面的均匀，没有明显的压力集中区域；而传统方案的压力场中存在局部高压和局部低压区。受阀芯壁面的导流作用，优化方案的流速分布更加平滑，过渡自然；而传统方案的速度场则相对紊乱，过渡不连续，对壁面的急速冲击现象较明显。

仿真云图的分析结果直观展示了滑阀工作时的内部流场状态。局部低压区域易产生空化现象，从而解释了液压阀在小开度启闭时产生振动的原因，致使液压阀控制不平稳。仿真结果证明了存在圆弧导流壁面时,液压阀内部流态得到了明显改善，为实现该比例伺服阀小开度精准控制提供了可行的优化思路。

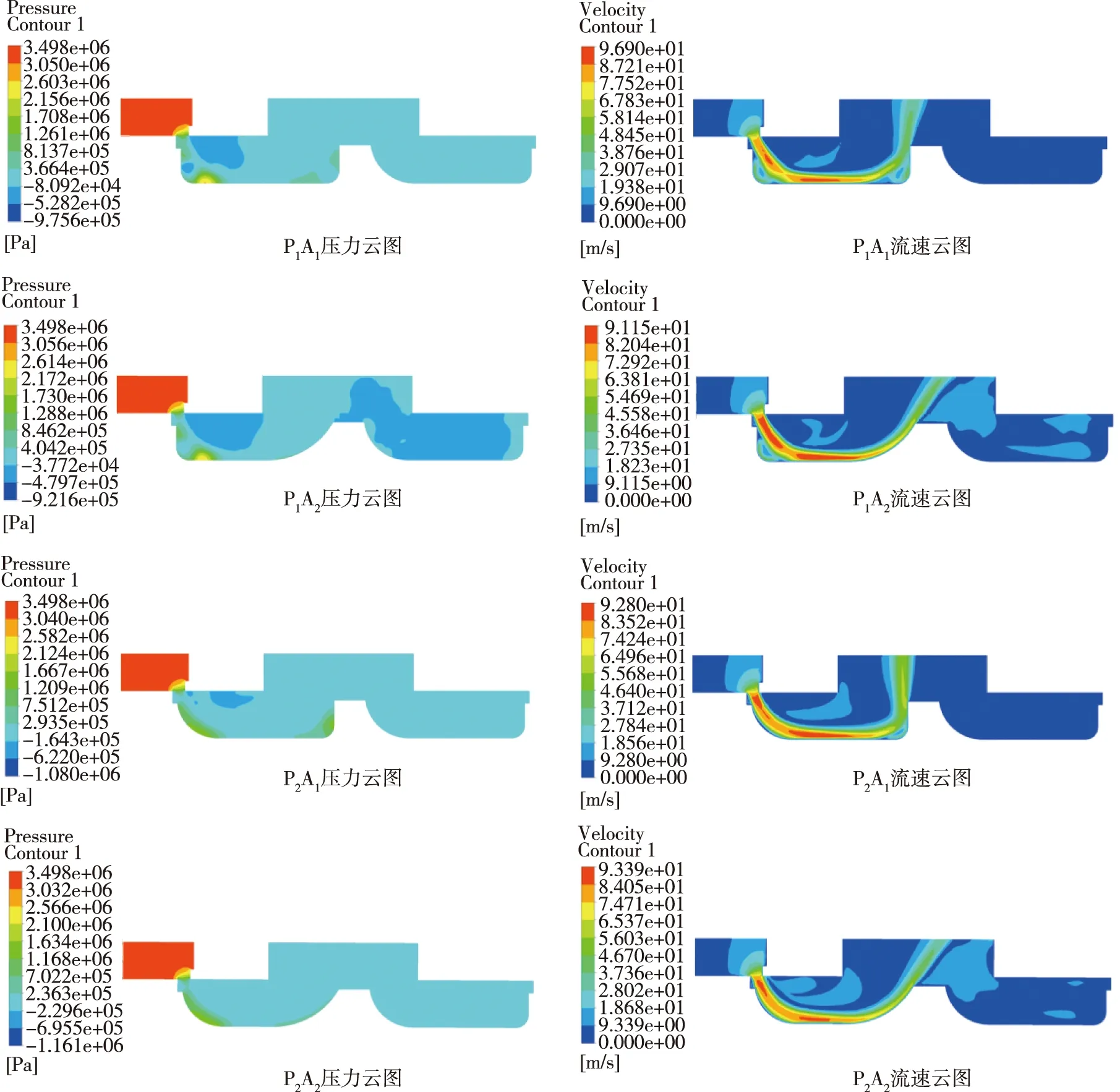
(a)P-A阀口的四种组合方案

3.2 液动力分析

将P-A、B-T的模型分别两两结合的十六种方案相对比，并对所有模型的仿真数据进行汇总分析，得到各方案在0～1mm开度范围内的流量和液动力变化曲线。以BT方案为例，单阀口从零开度至1mm开度状态时的流量及液动力变化曲线如图9所示。

将单个阀口的液动力仿真数值与阀口数量相乘，再将P-A、B-T各方案两两相加，得到所有方案阀芯所受总液动力数值。在本研究中，以阀芯所受最大液动力作为评估标准，汇总不同方案在0～1mm开度内的最大液动力值，结果如表3所示。

(a)流量变化曲线

表3 不同方案阀芯所受总液动力最大值(单位：牛)Tab.3 The maximum hydraulic power of different valve cores (unit：N)

根据表3数据，在两组结构方案中阀芯所受液动力情况受P-A阀口结构影响较大，受B-T阀口的影响相对较小，B、T阀口采用圆弧导流壁面结构对液动力的数值无明显优化作用。P-A阀口不同方案之间的液动力数值有明显差异：当采用PA方案，即P、A处均为传统垂直壁面结构时，最大液动力可达71.2N；而采用圆弧导流内壁结构的PA方案要比其他方案的液动力小很多，其液动力最大值仅为27.5N，比PA方案降低近60%。因此，在P-A阀口采用圆弧导流结构可显著提高比例伺服阀的力学性能，有效减轻液动力对阀芯的干扰。

以PA方案为基础，针对B-T阀口的仿真结果绘制不同开度时各方案的液动力变化曲线，如图10所示。可以观察到，阀口开度在0～1mm区间内，BT方案的液动力波动较小，其他方案的液动力数值波动较大。即当B处采用圆弧导流结构，P处采用垂直壁面结构时，液压阀整体所受液动力状态相对稳定，因此，采用BT方案时阀芯的控制性能相对较优。

图10 液动力随开度变化的曲线Fig.10 Curve of hydrodynamic force versus opening

4 结 论

液动力是影响比例伺服阀控制性能的主要干扰因素，研究阀芯所受液动力对液压阀性能提升具有指导性意义。本研究针对滑阀阀芯结构进行了优化设计，提出了阀芯壁面导流的液动力补偿方案，之后开展了液压阀内部流场的系列CFD仿真试验。通过仿真分析得到以下结论：

1)传统阀芯无导流内壁，其内部压力场中存在局部高压和局部低压区，且速度场紊乱，局部高速区域较明显；而优化结构中,受阀芯壁面导流作用的影响，压力和流线分布更加均匀，过渡自然，可有效减轻空化、振动等问题。

2)阀芯导流内壁优化设计结构可显著减小阀芯所受稳态液动力，与传统结构方案相比降低近60%，因此优化方案可明显改善比例伺服阀的力学和控制性能。