软件工具的三维功能在地理教学中的应用

乔永海

地理教学很需要展示三维动画的软件。GeoGebra软件不仅在数学领域有着广泛的应用，在地理学科也有很好地应用[1]，该软件的三维功能可以解决地理教学中的一些三维问题，这里列举几个案例，希望对各位老师有所启发。

一、 行星的椭圆运动

行星绕太阳运动的轨道是椭圆的，其运行速率也是变化的，近地点速度大，远地点速度小，遵守开普勒定律[2]。可以用GeoGebra制作出模拟行星运动的三维情境课件，如图1所示，行星的运动遵守开普勒定律。该课件还具有交互性，比如，等时间地按动“显示轨迹”按钮，能够显示出单位时间内行星和太阳连线扫过的面积是相等的，这是开普勒第二定律，即等面积定律。

二、 地球的公转及其带来的影响

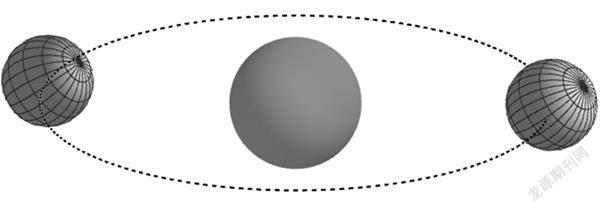
如图2所示，该课件展示的是地球绕太阳公转的三维情境，地球在转动过程中，地轴平行移动，而且和黄道面成固定角度，地球一边自转，一边绕太阳公转。从图2可以看出，当地球转到轨道的最左边时，太阳照射到北半球的面积最大，北半球白天时间长，黑夜时间短，这就是夏至日。当地球转到轨道的最右边时，太阳照射到北半球的面积最小，北半球白天时间短，黑夜时间长，这就是冬至日。课件展示的星体是立体的，它们的运动也是在三维空间中运行的，可以从不同角度观察其运动，能让学生获得关于天体运动的直观感受。我们平时经常对着静态的图形讲解运动，这种教学方式的直观性显得不足，学生想象这些看不见的运动是有困难的，该课件弥补了上述不足。

三、 数字地球仪

地球仪是把地球按照一定的比例进行缩小而制作的地球模型。地球仪在地理教学中的有重要用途。教学中地球仪的使用比较普遍，教师有示教的大型地球仪，学生经常会人手一个袖珍地球仪。在利用地球仪讲解相关问题时需要把地球仪透射到屏幕上，让更多的同学看到，这就需要数字地球仪了。一些智能白板提供了数字地球仪软件，还能够在地球仪上贴图，但功能上还是比较单一。用GeoGebra 软件制作的数字地球仪在功能上更加丰富，在教学中能发挥积极的作用。

1. 辅助讲解纬线和纬度

初学地理的学生对经度、纬度的理解是有困难的，纬度对应的是地球内部的立体角，借助数字地球仪可以让学生从空间上认识纬度。

如图3所示，在数字地球仪上显示了经线和纬线，然后把数字地球仪剖开，如图3右图所示，剖面有左右两个扇形平面，在右边的扇形剖面上，地球的中心为O，赤道上的一点为A，扇形剖面的弧形边是一条经线，B是该条经线上的一个动点。∠AOB就是过B点的纬线的纬度，沿着经线移动B点，∠AOB从0°增到90°，对应的就是过B点纬线的纬度。在北半球叫作北纬，在南半球叫作南纬。纬度实际上对应着地球内部的一个立体角，对纬度的理解需要一定的空间想象能力，借助该数字地球仪的立体功能，可以帮助学生从空间上理解纬度的概念，在头脑中形成正确的图景。

2.城市的定位

经纬网由经线和纬线共同组成，可以用来确定地球表面各个点的准确位置。我们可以在数字地球仪上绘制简易的世界地图，由于这些地图的边线是由很多空间折线拼接而成，所以，只能绘制各大洲的轮廓线。该数字地球仪具有实用性，比如，显示城市并确定该城市的位置，图4中的北京，从数字地球上能大致定出它的位置是北纬40°、东经116°。

四、 地月系和月球的运动

高考改革后，出现了同时报考物理和地理的学生，他们有了相对完备的高中物理基础，可以对一些地理问题进行深度学习，比如地月系的质心及其月球的运动问题。

高中物理学习了双星，靠得比较近的天体在彼此万有引力作用下互相缠绕着运动叫双星运动。双星围绕着公共的质心运动，质量越大的天体距离质心越近，质量越小的天体距离质心越远，其质量和轨道半径成反比。地球质量约是月球质量的81倍，地月的平均距离为d=384，403.9千米，因此，地心和地月质心的距离r1为

地球平均半径约为R=6371km，因此，质心距离地表R-r1=1683km，约为0.264R。很多同学认为月球绕着地心转，其实，月球和地球绕着地月系的共同质心转，同时，地月系公共质心又绕着太阳转，所以，相对于太阳，月球的运动轨迹是很螺旋状的曲线，如图5的点状虚线所示[3]。

我们可以把这些课件分发给学生，学生可以在自己的平板電脑上操作，增加对这些情境的感受。以上仅仅是 GeoGebra 解决地理教学问题的几个案例，希望感兴趣的教师结合地理教学实际，利用GeoGebra 软件开发出更多的能够解决地理教学难点的优秀课件来。