桥梁转体T构不平衡力矩测试技术研究

钟丹丹

（中铁二十五局集团第四工程有限公司，广西 柳州 545007）

0 引言

由于转体球铰体系在制作、安装、T构两端砼浇筑及梁体预应力施加存在操作误差等原因，转体T构两悬臂梁段重量作用于球铰中心的力矩不同，即存在不平衡力矩，过大的不平衡力矩会使T构沿连续梁纵轴线的竖平面转动，导致安全事故发生。为确保转体施工能够顺利、安全进行，需要对T构进行不平衡力矩测试（简称“称重”），以确定T构重心偏移量、制定配重方案、调整重心至合理区间内。本文依托南宁市亭洪路延长线（规划七路～南建路）工程上跨铁路立交桥主跨2-80.0 mT形钢构桥转体施工实践，详细阐述转体T构称重、配重的试验方法。

1 工程概况

南宁市亭洪路延长线（规划七路～南建路）工程上跨铁路立交桥工程，位于南宁市江南区铁路南化站附近，桥上设置双向六车道，按两幅设计。上部结构为单箱三室斜腹板箱形截面，2-80.0 mT形钢构桥按两幅桥进行布置，跨越既有南化站。

上部结构主桥T构采取满堂支架现浇后，再平面转体施工。为确保转体施工的安全进行，在转体前对T构进行称重，并据此配重、调整T构重心。

2 称重方法及原理

2.1 测试不平衡力矩的方法

本次不平衡力矩的测试（简称称重）方法为球铰转动法，该法通过向转体T构施加顶力，测试当T构位移突变（临界状态）时所施加的顶力，通过其此时的力矩平衡条件计算T构的不平衡力矩及重心偏移值[1]，作为转体施工决策和配重方案的依据。该法因操作简便、结果准确、费用低的优势而得到广泛使用。

测试前，拆除浇筑0号块的钢管支架，解除T构与承台间的固结措施，此时，上转盘及T构组成整体的刚体，然后对T构施加转动力矩，使转动力矩均匀、缓慢地增加，直到球铰结构两转盘间出现转动位移，即位移发生突变。此时，施加的外力矩使T构能够克服球铰静摩阻力矩而出现微小的相对转动，且处于静、动的临界状态。在此状态下，球铰间摩阻力矩（MZ）、T构的不平衡力矩（MG）及施加的外部力矩构成一种平衡状态。由此平衡条件可将摩阻力矩（MZ）、不平衡力矩（MG）计算出来。

2.2 计算球铰间摩阻力矩（MZ）和转体T构不平衡力矩（MG）

T构完成支架的脱离后，通常T构体系处于如下2种平衡形式之一：①形式1。如果没有撑脚支撑在滑道的钢板上，说明球铰间摩阻力矩（MZ）较转体T构不平衡力矩（MG）要大，故T构没有发生上、下转盘之间的转动。T构平衡状态是由转体T构不平衡力矩和球铰间摩阻力矩所构筑；②形式2。如果有撑脚支撑在滑道的钢板上，则表明不平衡力矩（MG）大于摩阻力矩（MZ），故T构球铰发生转动，直至撑脚支撑在滑道上，此时，转体T构的平衡状态是由转体T构不平衡力矩、球铰间摩阻力矩和撑脚反力力矩所构筑。

2.2.1 形式1平衡状态下的测设及数据计算方法

形式1平衡状态的称重方法为：分别从T构的东、西（如图1、图2所示）侧设置支点施加顶力，使转体T构沿纵轴的竖平面内出现顺、逆时针的微小转动。记录测试过程中位移传感器和压力传感器的读数。顶力逐级增加，当位移传感器的读数出现突变时，表示T构已产生转动、处于临界状态。

图1 在西侧施加顶力时T构力矩平衡关系

图2 在东侧施加顶力时T构力矩平衡关系

假定图1、图2中的不平衡为向东侧偏移，而球铰间摩阻力矩（MZ）总是相反于转动方向。根据转体T构在竖平面内的力矩平衡关系，计算过程如下：

由（1）、（2） 式计算出：

式中，P1、P2在T构产生微小转动时，在其西、东侧施加的外力值（kN）；L1、L2为顶力的合力对球铰中心的力臂（m）。

2.2.2 形式2平衡状态下的测设及数据计算方法

此状态下，T构因自身不平衡力矩大于摩阻力矩而转动，假定不平衡力矩（MG）向东偏移，即东侧的撑脚与滑道接触。此时称重方法为：先在T构东侧设置千斤顶支点进行施力，使转体T构沿梁纵轴的竖平面内出现顺时针微小转动，然后落顶，使T构发生微小逆时针转动。记录测试过程中顶升、落顶过程中突变时位移传感器和压力传感器的读数。根据图3、图4中转体T构在竖平面内的力矩平衡关系，计算过程如下：

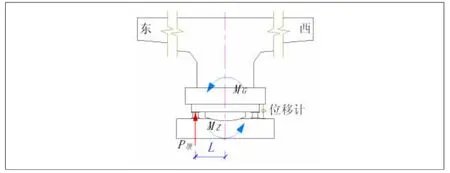
图3 东侧顶升T构力矩平衡关系

图4 东侧落顶T构力矩平衡关系图

由（5）、（6） 式计算出：

式中，P升、P落为T构产生微小转动时，在东侧施加（升、落）的外力值（kN）；L为施力合力对球铰中心的力臂（m）。

2.3 球铰静摩擦系数及T构偏心距计算

本项目采用四氟乙烯制作铰片，在上下转盘间填充黄油，根据相关文献的研究成果，采用下式计算球铰静摩阻系数、偏心距[2]。

式中，N为转体T构的总重量；R为球铰弧形的圆半径。

3 称重的实施

3.1 估算千斤顶与压力传感器的吨位

T构重量荷载F总=140 000 kN。按以往的工程实际，静摩擦系数μ的取值范围为0.05～0.07[3]。球铰的半径R为7.992 m，角度为28.985度，摩擦系数取大值（0.07），按公式（8）可计算得静摩擦力矩为

本次称重在上转盘承台下施加顶力，顶力距球铰中心线约为5.0 m，称重时在转盘两侧共设置6台千斤顶对（即每侧3台）T构施加顶力。则每台千斤顶需要的顶力计算得：35 882.41/（3×5.0）=2 392.16 kN。

考虑到加载时的对称性及施力时的安全性，每侧配备5000 kN千斤顶3台，相应配置5000kN压力传感器。

3.2 测试仪器和设备

（1）位移传感器。本项目设置6个传感器量测T构的微小位移，采用应变式位移传感器，该类型传感器不易受其它因素干扰，适用性强，其测量精度为1/1 000，量程为±5mm，线性度大于0.2%。

（2）压力传感器。设置6个压力感器以测量T构对千斤顶的反力，压力传感器型号为BLR-3型，其测量精度为±1%。，量程为5000kN，灵敏系数为2.0。

（3）数据采集系统。为满足称重测试的要求，采用IOTECHWaveBook512数据采集系统，其采样率为100万次/s；分辨率为12bit；有40个电压通道，16个动态应变通道。

（4）数据分析软件系统。数据分析软件系统引进美国的DADiSP数据分析软件包，该软件包能够对测试所得数据进行自动、直观的处理及分析。

（5）I20a工字钢基座。基座带加劲肋，长度约为60 cm，根据支撑点数量、千斤顶高度及支点处上下承台间的间距确定工字钢基座数量、设置厚2 cm的50 cm×50 cm钢板（每个支点2块）共6块。

3.3 解除临时固结措施，拆除砂箱及撑脚下的沙盘

在解除临时固结措施和拆除砂箱及撑脚下的沙盘之前，在上承台四周埋设千分表记录初始读数。拆除过程中注意每拆除一组支撑，观察千分表并记录读数，并观察随着砂箱的拆除，撑脚是否向一侧连续下沉。完全拆除后测定撑脚与滑道之间间隙变化和梁体竖向位移，并据此判断转体体系处于何种平衡方式，进而确定称重方案。

3.4 判定转动体系的平衡状态

当所有支撑完全拆除后，根据测定撑脚与滑道之间间隙变化和梁体竖向位移，判断转体体系的平衡状态。

（1）如果全部撑脚处于悬空状态，表明MZ（球铰摩阻力矩）＞MG（T构不平衡力矩），采用纵向两侧分别测试不平衡力矩的方案。

（2）如果撑脚与滑道钢板产生接触，相对应的另一侧撑脚与滑道钢板相距缝隙变大，表明MZ（球铰摩阻力矩）＜MG（T构不平衡力矩）。假定不平衡力矩MG向东偏，先在T构东侧顶升梁体，当T构沿纵向轴线的竖平面发生微小转动后再落顶，直至T构发生微小转动。

3.5 试验实施

本项目先进行左幅桥T构的称重，全部拆除砂箱、固结措施后，观察到左幅桥T构处于第1种平衡型，故按下程序进行称重试验：

（1）将千斤顶置于撑脚与滑道间隙较小的那一侧，安装钢墩、钢板及传感器等。

（2）调整千斤顶，施加初始顶压力至全部千斤顶，对加载体系进行预顶、记录此时油表读数。

（3）千斤顶回油卸落后与转动体稍微脱离，使压力传感器、千分表凋零。

（4） 千斤顶逐级加力，级差大约控制为300～500 kN，记录各级的力值，并记录相应的位移，持续加载至位移突变。绘制“力—位移（P△）”曲线，找出临界状态的拐点。

（5）每侧加载平行测试两次，并对结果进行比较（若两次结果偏差过大，重新测试）。

（6）从另侧顶升，重复实施上述测试。

3.6 测试仪器的布置

在左幅桥T构的东、西两端，距球铰中心5.0 m处分别布置3台千斤顶，在千斤顶上安装压力传感器（布置方法如图5所示）。

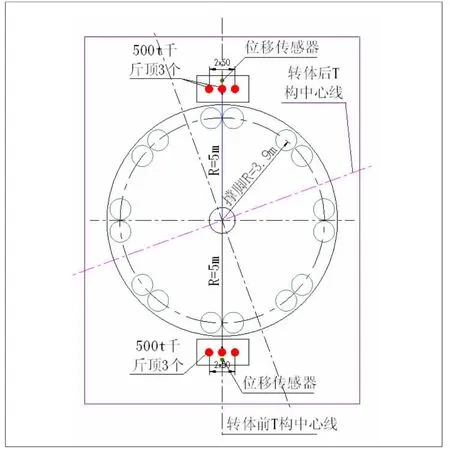
图5 称重试验设备及测点布置图

4 试验数据处理及配重方案

根据上述称重试验的数据，绘制并分析“力—位移（P△）”曲线图（如图6所示），找出临界状态的拐点，确定临界状态时的顶升力（P）。

图6 左幅桥T构称重的P△曲线图

（1） 左幅桥T构

因左幅桥T构是第1种平衡形式，称重完毕后，绘制并分析“力—位移（P△）”曲线（如图6所示）。由公式（3）和公式（4）可计算出不平衡力矩（MG）和摩阻力矩（MZ）。

进而根据公式（10）算出静摩擦系数（u），根据公式（11） 算出偏心距（e）。

测试数据的分析计算结果见表1。

表1 左幅桥T构称重测试分析计算表

分析表1所列的计算数据，左幅桥T构的两端存较不平衡力矩，偏心距e=0.33 m，位于东侧。由于偏心距过大（设计要求偏心距≤5 cm）。该转体T构采取在西侧距球绞中心65 m处设置配重的方案，完成配重后，再进行称重，得调整后的偏心距e=2.1cm，达到转体要求。

（2） 右幅桥T构

右幅桥T构也是第一种平衡状态，测试数据的分析计算结果见表2。

表2 右幅桥1号墩T构称重测试分析计算表

分析表2所列的计算数据，右幅桥T构的两端虽存在一定的平衡力矩，偏心距e=0.029 m，位于东侧。由于偏心距≤5 cm，故转体T构的重心偏移在误差允许范围内，不需重新调整。

5 结语

本项目的T构球铰转动法称重采用压力传感器、位移传感收集与传输试验数据，运用先进处理软件对数据进行分析、处理及直观显示，使试验更科学、测试结果更精准、数据处理更快捷。达到准确测试转体系统的不平衡力矩的目的，为调整重心配重提供决策依据，确保转体施工安全、顺利。同时，还能够通过测试所得数据计算出摩阻系数、摩阻力矩，作为转体施工时牵引力的计算依据，保证牵引系统转体时的安全可靠性。