基于PCA-BP神经网络的北京市耕地面积预测
娄在鹏 谢国磐 刘 璇 张宝雷
(1)山东师范大学地理与环境学院,250358,济南; 2)山东省土地储备中心,250014,济南;3)山东省土地发展集团有限公司,250014,济南)
1 引 言
粮食安全是国家安全基础,耕地的数量、质量是确保粮食安全的根基[1],随着经济发展,建设用地对耕地的占用也产生了一系列的问题[2-4],耕地保护一直是土地管理工作的重中之重.科学预测耕地数量是耕地保护的基础,并制定有效政策保证耕地数量,对缓解用地矛盾、保证粮食安全和维持区域生态平衡具有重要指导意义.
当前,国内外对耕地面积预测方法较多,除神经网络预测外,比较常用的有线性回归模型等纯数据趋势预测方法[5],考虑影响因素权重的灰色预测方法[6,7],考虑地类间相互转换的马尔科夫模型法[8-10]以及元胞自动机[11,12]等,上述方法虽然取得了一定的预测效果,但是仍然存在模型应用的局限性,如纯数据趋势预测方法难以避免内生性问题,灰色预测模型不适宜处理低随机样本数据;马尔科夫模型限于应用到短期预测等,另外,上述模型忽略了耕地面积的变化是一个多因素、多反馈的复合系统,受到自然与经济因素的复合影响,且模型预测精度存在一定的误差.人工神经网络更适合处理模糊的、非线性、含有噪音及模式特征不明确的问题[13],它具有良好的非线性映射逼近性能,可以较好的拟合变量之间的相关关系,从而得到良好的预测效果[14],然而BP神经网络对输入变量的条件存在限制,且应用到耕地面积预测的文章较少,因而建立新型易应用高精度的BP神经网络以运用到耕地面积预测成为当前研究的热点问题.
北京市是全国耕地面积减少最快的地区之一[15], 耕地流失是北京土地利用变化的核心问题.本文以北京市为例,选取了16个影响因素,从因素角度出发,采用BP神经网络,应用主成份分析(PCA,Principal Component Analysis)对原始变量降维处理,减少变量个数以及变量间的共线性,从而将所有变量转换为与耕地面积贡献率最高的主成分[16],解决神经网络输入变量的条件限制并提高神经网络运行效率,在影响因子预测方面,从时间角度出发,选用灰色预测模型以及指数平滑模型进行预测互补,为PCA-BP神经网络的下一步预测提供准确的数据基础,并同时对耕地面积进行预测,以验证PCA-BP神经网络的预测精度,为土地资源的可持续利用和土地规划的合理安排提供决策依据.
2 数据与方法
2.1研究区与数据来源北京市地处华北平原北部边缘,四周与河北省、天津市相邻,全市下辖16个区,总面积1 642.00 hm2.2019年末,常住人口2 153.6万人城镇化率86.6%,常住外来人口达794.3万人.2009年-2018年,北京市耕地面积由231 600 hm2减少到213 730 hm2.本研究选取的可能影响耕地面积变化的因子有地区生产总值(X1)、第一产业增加值(X2)、第二产业增加值(X3)、第三产业增加值(X4)、人均地区生产总值(X5)、人口数(X6)、全市家庭恩格尔系数(X7)、城市人均可支配收入(X8)、城镇人均消费支出(X9)、农村人均可支配收入(X10)、农村人均消费支出(X11)、一般公共预算收入(X12)、一般公共预算支出(X13)、全社会固定资产投资(X14)、外商投资额(X15)、建筑业总值(X16)等16个,均来自《中国城市统计年鉴》(2008-2017年)和《北京市统计年鉴》(2008-2017年).
2.2研究方法
2.2.1 灰色预测模型(GM(1,1)) 在基础上弱化原始数据的随机性,建立了灰色模块,微分拟合方法直接应用于时间序列变换到微分方程,建立了发展和变化模型,这是一种使用不足信息建立可能的足够的信息模型,单变量灰色预测模型包含三类:传统GM(1,1)模型、新信息GM(1,1)模型和新陈代谢GM(1,1)模型,三者计算公式均一致,不同的是对原数据序列的处理方式,新信息GM(1,1)模型将预测得到的新数据加入原始数据序列末端形成新原始序列进行预测,新陈代谢GM(1,1)则是将预测得到的新数据加入原数据列末端的同时,将原数据的首个数据剔除形成新数据序列,从而进行预测.传统GM(1,1)模型计算公式为[8,17]:
(1)
式中,x(1)(t)为x(0)(1)的一次累加值,且x(0)(t+1)=x(1)(t+1)-x(1)(t);t为时间;a,u为模型参数.
2.2.2 Brown线性趋势模型(Brown′s linear trend) 该模型为指数平滑模型其中之一,适用于具有线性趋势并没有季节性的时间序列.其平滑参数是水平和趋势,并假定二者等同.因此,Brown模型是Holt模型的特例,可以为未通过灰色预测模型后验差检验的数据进行时间序列分析,其计算公式为[18]:
lt=αxt+(1-α)(lt-1+bt-1).
(2)
bt=β(lt-lt-1)+(1-β)bt-1.
(3)
xt+h=lt+hbt,h=1,2…
(4)
式中,t为当前期;h为预测超前期数,也称之为预测步长;xt为第t期的实际观测值;lt为时刻t的预估水平;bt为时刻t的预测趋势(或坡度);α为水平的平滑参数;β为趋势的平滑参数.
2.2.3 PCA-BP神经网络
1)灰色关联分析.对所获取的数据进行定量筛选时,常用皮尔逊相关性分析或者斯皮尔曼相关性分析,本文应用灰色关联分析,它能更好地度量各种相关因素之间的相关程度,能克服传统多元相关分析和多元回归分析的缺陷,是一种能更好地求解多因素之间的相关关系的重要数学方法[19],计算过程分为数据变换,关联系数(式5)与关联度的计算(式6)(如下)[20]:
参考数列:x0=(x0(1),x0(2),x0(3)),…,x0(n)
比较数列:xi=(xi(1),xi(2),xi(3)),…,xi(n);i=(1,2,…,n)
(5)
式中,loi(k)为k时刻两比较序列的绝对差,Δmin和Δmax分别为比较序列各个时刻绝对差的最小值和最大值.ρ为分辨系数,一般情况下取0.5.
(6)
式中,roi为子序列与母序列关联度;N为比较数列的长度.
2)主成分分析(PCA).利用协方差矩阵的特征向量和对应的特征值,识别各个主要影响成分.选取对应最大特征值的分量作为第一个主成分,该变量对其他数据的变异性影响最大,代表沿着描述最大扩散轴的原始数据分布方向.以此类推,可以逐步确定出第n个主成分,这些主成分之间互不相关,且方差递减[21].
3)BP神经网络.BP神经网络分为前、后传播两个方面,在向前传播的过程中,输入信息受到输入层的处理,再经隐含层到达输出层(见图1),再此过程中下层神经元状态仅收到上层神经元的影响,在未达到期望输出时,信号将进行反向传播,并对途经的神经元进行权值修改,经过此过程的反复迭代,最终得到期望输出.计算步骤为,

图1 BP神经网络结构
设置各权值或阈值初始值wji,bj.
选择训练样本,输入向量P=(p1,p2…pR),期望输出向量T=(t1,t2…tR),对每个输入样本进行后续步骤的迭代;
计算网络的实际输出以及隐含层的状态:
(7)
式中,akj—第k个样本在第j层的输出;wji—第j层和第i层的连接权值;aki—第k个样本在第i层的输出;bj—第j层的阈值.
误差计算
δkj=akj(1-akj)(tkj-akj).
(当j为输出层时)
(8)
(9)
权值和阈值的修正
ωji(t+1)=ωji(t)+ηδjaki+α[ωji(t)-ωji(t-1)]
(10)
bj(t+1)=bj(t)+ηδj+α[bj(t)-bj(t-1)]
(11)
当k每经历1至p后,根据是否达到要求进行判断,满足则算法停止.
3 结果与分析
3.1GM(1,1)模型预测首先,对耕地面积进行准指数规律检验,光滑比小于0.5的数据占比为88.89%,除去前两个时期外,光滑比小于0.5的数据占比为100%,准指数规律检验通过,以最后三年作为实验组,应用传统GM(1,1)模型、新信息GM(1,1)模型以及新陈代谢GM(1,1)模型三种预测模型进行建模处理得到相关模型参数(表1),选取模型参数中SSE最小的新信息GM(1,1)模型作为最优模型[19],得到预测方程(式12),后验差检验得到(C,P)为(0.22,1),后验差检验通过,同时平均相对残差和平均级比偏差分别为0.004和0.006,表明模型精度很好可以进行预测.

表1 模型参数
x(1)(t+1)=-38 974 651.569 081 5e0.005 808 3t+39 206 252.449 081 5
(12)
3.2指数平滑模型预测应用SPSS26.0,对耕地面积以进行时间序列分析,使用专家建模器进行指数平滑或ARIMA模型最优选择(表2),结合平稳序列自相关(ACF)图和偏自相关(PACF)图来检验残差序列是否显著自相关,若ACF或PACF图内残差均位于置信区间(黑色实线)以内,说明拟合后的残差序列为白噪声序列.结合图(2)与表(2)表明,模型拟合后的残差序列为白噪声序列,R2为0.939,模型检验通过且拟合度很好,建立预测方程(式13,14,15).
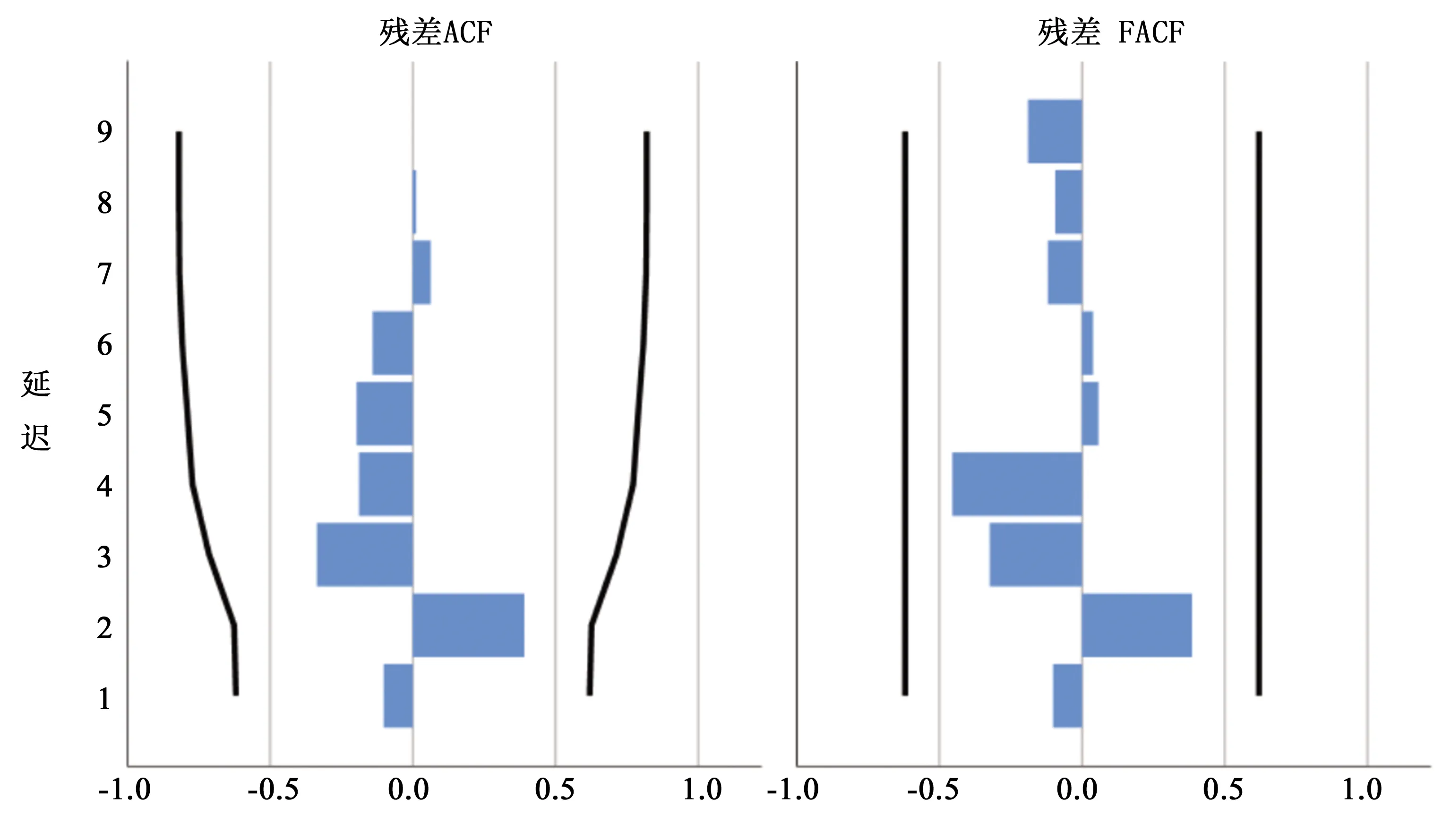
图2 耕地面积残差ACF与PACF图
lt=0.988xt+0.012(lt-1+bt-1)
(13)
bt=0.988(lt-lt-1)+0.012bt-1
(14)
xt+h=lt+hbt,h=1,2…
(15)
3.3PCA-BP神经网络预测
3.3.1 灰色关联分析 对原始数据进行灰色关联后,得到耕地面积与地区生产总值等16个因子的灰色关联度(表3),选取关联度大于0.7的15个影响因子.

表3 因子灰色关联度
3.3.2 主成分分析(PCA) 对15个影响因子进行主成分分析,根据所得的累计贡献率结果,选取PC1、PC2和PC3等3个主成分,累计贡献率达99.69%,符合高于85%的标准.针对选出影响因子使用GM(1,1)模型,在相关检验(C<0.35,P>0.95)通过的前提下(表4),建立GM(1,1)模型预测方程(表5),未通过检验的因子(X2)使用3.2中专家建模器进行分析,得到时间序列分析模型为Brown 线性趋势模型,图3与表6表明,模型拟合后的残差序列为白噪声序列,R2为0.775,模型检验通过且拟合度较好,建立预测方程(式16),综合以上因子预测方程得到2022年与2027年影响因子数据,结合得分系数矩阵反算得出预测数据的主成分得分及其预测值,进一步进行归一化处理得到表7.

表7 归一化样本数据
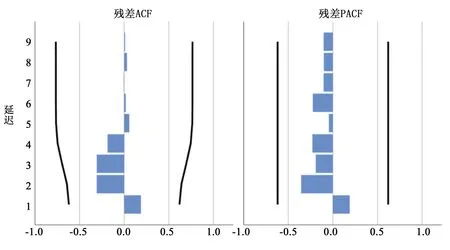
图3 因子X2残差ACF与PACF图

表4 GM(1,1)模型相关参数

表5 GM(1,1)预测方程

表6 模型拟合度
3.3.3 BP神经网络预测 根据输入的3个主成分得分归一化数据,以及输出的归一化后的耕地面积数据,确定输入层节点为3,输出层节点为1,隐含层节点为10,学习速率为0.01,以2013和2014年数据为实验样本,其他数据作为训练样本,选用trainbr为训练函数,进行神经网络训练,最终得到训练误差为0.000 99,模型可以进行预测,得到2022年和2027年耕地面积分别为208 211.77 hm2和205 929.69 hm2.
xt+h=(h+1)xt-hxt-1,h=1,2…
(16)
4 精度评价与趋势分析
4.1精度评价以实际耕地面积为X轴,以模型预测值为Y轴,建立平面直角坐标系,在该坐标系上散点与直线y=x的距离越远,表示模型预测的误差值越大,由图4以及表8、9可知,R2均大于0.9且误差相对百分比小于5%,表明三种模型拟合度较高.

图4 样本实际面积与模型拟合值
平均绝对误差(MAE)、均方根误差(RMSE)和平均预测精度(R)计算公式为[24,25],
(17)
(18)
(19)

进一步用平均绝对误差(MAE)、误差均方根(RMSE)和平均预测精度(R)来进行精度比对(式17,18,19),得到模型比较结果(表8),GM(1,1)模型、Brown线性趋势模型和PCA-BP神经网络的MAE分别为871.73、972.85和650.96,RMSE分别为1 003.05、1 196.25和876.53,R分别为99.60、99.56和99.70,在误差方面,BP神经网络的MAE与RMSE的值均小于其他模型,在平均预测精度方面,PCA-BP神经网络精度高于其他模型,从而证实了PCA-BP神经网络具有良好的预测能力.

表8 模型拟合值及误差值
4.2趋势分析由上述分析结果可得出,北京市耕地面积由2017年到近期2022年,耕地面积减少6 048.69 hm2,年均减少1 209.74 hm2,下降率为0.7134%,由2017年到远期2027年,耕地面积减少2 282.08 hm2,年均减少456.42 hm2,下降率为0.2751%.不难看出,随着时间推移,耕地面积减少速率变缓,其主要原因是随着经济发展和社会进步,我国经济逐渐转入中速增长期,经济的发展转向质量上来,同时,在相关科技与技术进步的推动下,建设用地由平面扩张转向空间立体式发展,进而间接导致耕地面积缩减减缓.
5 结 语
1)本文在进行影响因子预测时,从时间角度出发,采用多种GM(1,1)模型进行综合比以及后验差检验通过后,选择最优GM(1,1)模型来进行因子数据的预测,对未通过检验的因子,使用时间序列分析中专家建模器得到最适合的Brown 线性趋势模型,在残差检验通过后进行预测,两模型互补预测从而保证了因子预测数据的精准度,为进一步使用PCA-BP神经网络预测提供了数据基础,另外,对针对BP神经网络的变量输入限制问题,使用GRA、PCA进行优化取得了良好的效果,为未来耕地面积预测提供了模型构建思路.
2)通过精度对比可以发现,PCA-BP神经网络的MAE(650.96)与RMSE(876.53)低于GM(1,1)模型和指数平滑模型,同时R(99.7)值高于GM(1,1)模型和指数平滑模型,从而证明PCA-BP神经网络可作为一种良好的预测模型进行预测分析,但上述三种模型在表9中没有较为明显的差异,推测有两种原因,一是本文的北京市耕地变化数据与时间变化呈一定的相关关系且数据波动性较不明显,导致时间序列分析以及灰色预测分析与神经网络的预测效果接近,二是在进行预测过程中,笔者对三类模型同时进行了优化处理,使得三者的预测效果均取得了良好的预测效果,未来将加强研究原始模型与优化模型的分析对比,以取得更好的实验效果.

表9 模型比较情况
3)从结果分析可以看出,北京市由2017年起,耕地面积减少速率减缓,分别于2022年和2027年耕地面积达到208 211.77 hm2和205 929.69 hm2,为土地资源的可持续利用和土地规划提供了基础.对于北京市等中心城市,可通过积极打造卫星城等措施,充分发挥辐射以及带动作用,拉动周边城市经济发展的同时,减少自身耕地资源不必要的浪费,另外,要充分发掘城市地上与地下空间潜力,主动打造立体性城市,为守住耕地保护红线提供保障.
4)PCA-BP神经网络虽然在进行用地面积上预测较好,能够进行多因素的非线性拟合,达到较高的精度,但学习速度较慢以及对参数调节存在一定的要求,建模条件较为苛刻,有待于进一步的研究与优化.

