提高数学阅读能力的探究
孟祥菊 闫 雪
(保定学院数据科学与软件工程学院 河北·保定 071000)
阅读是理解、是吸收、是收获、是丰富、是人生必然的经历,而数学学科有其自身的教学特点,所以“数学阅读”一定有它特殊的意义与策略。数学需要阅读,在阅读中掌握概念,在阅读中体会定理内涵。在阅读中理解题意,在阅读中培养数学阅读能力,从而达到解决数学问题的目的,见参考文献[1]-[5]。
1 以“疑”导读
以“疑”导读就是带着问题读,在阅读中发现问题、提出问题。
例:如图1,某市A,B,两地之间有两条公路,一条是市区公路AB,另一条是AD-DC-CD外环公路这两条公路转成等腰梯形ABCD,其中DC//AB,AB:AD:DC=10:5:2.

图1
(1)求外环公路总长和市区公路长的比;
(2)某人驾车从A地出发,沿市区公路去B地,平均速度是 40km/h,返回时沿外环公路行驶,平均速度是80km/h,结果比去时少用了,求市区公路的长。
下面分析一下学生做这道题应如何设疑解决问题。
问题1:这两条公路转成等腰梯形有什么用呢?
回答1:如果四边形ABCD是等腰梯形,那么AD=BC。
问题2:外环公路总长和市区公路总长分别是多少?
回答2:外环公路总长为AD+DC+BC,市区公路总长为AB。
解:(1)设市区公路总长为10xkm,则CD=2xkm,AD=5xkm
∵四边形ABCD是等腰梯形,
∴BC=AD=5x
∴AD+DC+CB=12x为外环公路总长,即外环公路总长和市区公路总长比为12x:10x=6:5
问题3:上一问已设市区公路总长为10xkm,如何列方程呢?
回答3:题目中已分别给出两条路的速度,可以求出时间。
问题4:求出时间如何利用时间列等式呢?
问题5:哪条路用的时间长?
回答5:根据题意,行驶在市区公路上的时间较长。
解:(2)由(1)可知市区公路总长为10xkm,则外环公路总长为12xkm.由题意可得
解得x=1,即10x=10
答:市区公路总长为10千米。
这道题并不难,然而有些同学不能得到满分,其中大部分失分是因为第二问不会解答,还有小部分是因为第一问解错了从而导致第二问得不到正解。正所谓“学贵质疑,小疑则小进,大疑则大进。”质疑的过程是学生逐步理解问题的过程,也是思维能力发展、自学能力提高的过程。学生在阅读时要学会“标新立异”养成爱问、好问、会问的好习惯,从而在阅读中发现问题、提出问题、分析问题、解决问题。这样一来,学生在阅读过程中就会抓住重点,提出更多疑问,思维也得以开拓,成绩自然就会提高。
2 以“动”带读
以“动”带读就是边读边做、边读边画、边读边写。将题目的关键点列出来,进而使题目变得更简单、更清晰一些。
例:如图2,四边形ABCD是正方形,点E,K分别在BC,AB上,点G在BA的延长线上,且CE=BK=AG.
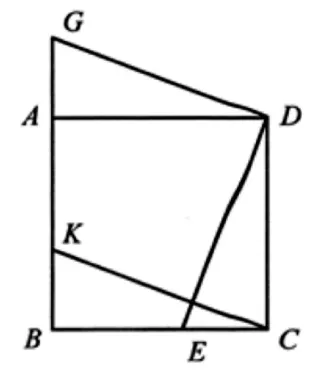
图2
(1)求证:①DE=DG;
②DE⊥DG;
(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求只保留作图痕迹,不写作法和证明);
(3)连接(2)中的KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想:
下面分析一下学生在做这道题时应如何勾画关键解决问题。
关键1:想要证明两条线段相等,即DE=DG,我们首先会想到利用全等三角形,这两条线段分别在哪两个三角形中呢?
解答1:三角形DCE和三角形DAE。
关键2:三角形全等的条件有哪些?该题应该应用哪个?
解答 2:已知 DA=ADC,CE=AG,∠DCE= ∠DGA
关键3:DE⊥DG,也就是∠EDG=90°该如何证明呢?
解答 3:∠CDE+ ∠EDA=90°,又∠CDE= ∠ADG,所以∠ADG+∠EDA=90°
证明:(1)∵四边形ADCD是正方形,∴DC=DA,
∠DCE= ∠DAG=90°.
∠EDC=GDA,
又∵∠ADE+∠EDC=90°,∴∠ADE+∠GDA=90°,即DE⊥DG.
关键4:尺规作图要求画正方形有什么特点?
解答4:四条边都相等,利用圆的性质作图。
关键5:什么四边形是特殊的四边形?按要求作图。
解答5:由图观察可知,该四边形为平行四边形。
关键6:平行四边形的判定定理有哪些?
解答6:两组对边分别平行或相等,一组对边平行且相等,对角线互相平分。
关键7:添加对角线会更加麻烦,那么该从哪条边入手?
解答7:显然CK=EF,再证明CE=KF或CK//EF即可。
解:(2)如图 3

图3
猜想:(3)四边形CEFK为平行四边形。
证明:设CK、DE相交于M点,
∵四边形ABCD和四边形DEFG都是正方形,
∴AB//CD,AB=CD,EF=DG,EF//DG,
∵BK=AG,∴KG=AB=CD,即四边形CKGD是平行四边形,
亦即 CK=DG=EF,CK//DG,
∠KME=∠GDE=∠DEF=90°
∴ ∠KME+ ∠DEF=180°,即 CK//EF,
故四边形CEFK为平行四边形。
关键8:面积之比等于边长的平方之比,那么求边长之比显然利用勾股定理。

这道题目看似有些难度,但是有些得分点是需要学生动手作图去解决的。有些几何题就是这样,学生只需要边读题边动手去画一画,答案就会很明显不需要刻意去证明.对于点、线段较多的图形,可以从问题出发找出解决该问题的关键点和有用的条件,在演算纸上简单列出条件、问题,这样学生就可以将复杂的题目转化成简单地题目。如果题目未给出图形,学生可以在演算纸上做出大致的线段图或几何图,然后标注字母和数字,这样一来抽象的题目也会迎刃而解。所以说以“动”带读这种方法可以提高学生对题目的理解能力以及对培养学生抽象思维能力有着重要作用。
3 以“议”促读
以“议”促读就是读读议议,在阅读过程中相互交流从而发现问题,然后通过讨论、相互协作进而解决问题。
例:如图 4,A(-5,0),B(-3,0)。点 C 在 Y 轴的正半轴上,∠CBO=45°,CD//AB,∠CDA=90°,点 P 从点 Q(4,0)出发,沿X轴向左以1个单位长的速度运动,运动时间为t秒。

图4
(1)求点 C 的坐标;(2)当∠BCP=15°时,求t的值;(3)以点P位圆心,PC为半径的⊙P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求的t值。
下面分析一下学生在做这道题时会如何探讨解答。
讨论1:由已知可得△BOC为等腰直角三角形,并且点C在Y轴上方。
结论 1:BO=CO=3,所以 C(0,3)。
讨论2:当∠BCP=15°时有两种情况,即点P在点B的右侧,点P在点B的左侧。
结论2:当点P在点B的右侧时,则∠PCO=30°;当点P在点B的左侧时,则∠PCO=60°,所以t应有两种取值。
讨论3:当⊙P与四边形ABCD的四条边相切时有三种情况,即分别与边BC、CD、AD相切。
结论3:当⊙P与边BC相切时,则PC⊥BC;当⊙P与边CD相切时,则PC=OC;当⊙P与边AD相切时,则PC=OP。
解:(1)∵∠BCO=CBO 45°,∴OC=OB=3
又∵点C在Y轴的正半轴上,∴点C的坐标为(0,3)
(2)当点P在点B右侧时,如图5,

图5
当点P在点B左侧时,如图6,由∠BCP=15°,

图6
(3)由题意知,若⊙P与四边形ABCD的边相切,有三种情况:
①当⊙P与BC相切于点C时,有∠BCP=90°,从而∠OCP=45°得到 OP=3,即时 t=1。
②当⊙P与CD相切于点C时,有PC⊥CD,即点P与点O重合,此时t=4。
③当⊙P与AD相切时,由题意,∠DAO=90°,
∴点A为切点,如图7
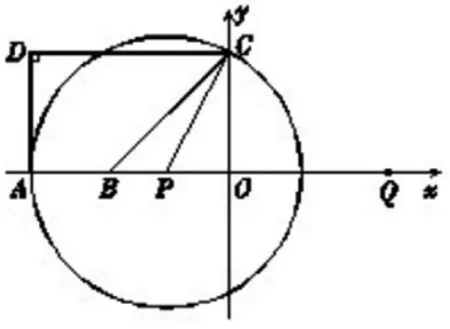
图7
PC2=PA2=(9-T)2,
PO2=(t-4)2
即(9-t)2=(t-4)2+32。得 t=5.6,故 t=1或 4或 5.6。
这道题目难度不大,但学生不易得满分,因为解题过程需要分多种情况进行讨论,而学生往往考虑不全面,总是会丢情况。而以“议”促读这种学习方法可以帮助学生在讨论的过程中理解题意或发现规律,养成思考缜密、考虑周全的做题习惯,从而不易因马虎的毛病而失分;同时这种学习方法也能培养学生思维的深刻性、多样性和创造性,进而提高学习效率。尤其是对于那些思维不太敏捷的学生来说,这种方法可以拓宽他们的知识获得渠道,深刻他们的记忆与思维,使其在讨论中不仅汲取了知识,还享受了学习的乐趣。
4 以“比”引读
以“比”引读就是在阅读的过程中通过比较将知识内化,从而对其联系与差别进行区分和整理。
例:下列运算中,正确的是( )
A、2x-x=1 B、x+x4=x5C、(-2x)3=-6x3D、x2y÷y=x2
下面再来分析一下这道题,该题目主要考察整式的除法、合并同类项以及幂的乘方与积的乘方这几个知识点。学生在学习此知识时应将这几个概念进行比较练习,总结出会经常出现的错误运算以免在考试中出现类似的错误而失分。
解:A、中整式相减,系数相减再乘以未知数,即2x-x=x,故本选项错误;
B、不同次数的幂的加法,无法相加,故本选项错误;
C、整式的幂等于各项的幂,即(-2x)3=-8x3故本选项错误;
D、整式的除法,相同底数幂底数不变,指数相减。故本答案正确。故选D。
以上四点就是对于如何提高数学阅读能力的所给出的方法和策略,但是在运用这些方法的同时学生应把握好四个关键,即眼到、口到、手到、心到。
首先,阅读的前提是眼到,因为每一个小细节,小问题都需要我们用眼睛去发现。在阅读的过程中学生要做到聚精会神,否则会由于马虎丢读某个数字或符号而失分等。
其次,阅读的基础是口到,因为不管是语文阅读还是数学阅读都需要用嘴巴将信息复述出来,这样有利于对知识或题目的记忆,从而加深印象。
再次,阅读的重心是手到,因为每一次阅读都会有重点或有用的信息,需要将其勾画或列下来,尤其是几何题更需要动手画图方便解题。
最后,阅读的精髓是心到,因为做任何事都需要用心,尤其是学习。学生在阅读的过程中应做到一心一意、全神贯注,要真正的用心去体会、去领悟。否则,很简单的题目也会因为你的心不在焉而变得很难。

