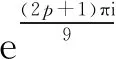某些链环琼斯多项式的零点性质
韩友发, 张宇浓, 燕佳钰, 姜明慧
(辽宁师范大学 数学学院,辽宁 大连 116029)

本论文主要分为两个部分,第一部分介绍一些基本知识,包括纽结链环的定义,Alexander多项式和Jones多项式的表达形式与性质;第二部分,重点讨论了排叉结P(k,1,…,1)和P(k,k,k)的琼斯多项式的零点分布性质,给出了某些单位根不是解的证明.
1 预备知识
1.1 纽结的基本概念
定义1.1把嵌入欧式空间R3或者三维球面S3中的圆周S1称为纽结.若给纽结规定一个方向,则得到有向纽结.
定义1.2由有限条互不相交的简单闭曲线构成的图形,称为链环;组成链环的每一条闭曲线称为该链环的一个分支;如果给链环的每一个分支规定一个方向,则称该链环为有向链环.
定义1.3对有向投影图L的全体交叉点符号(+1或-1)(见图1)求和,结果称为L的拧数,记作ω(L).

图1 交叉点符号
1.2 纽结多项式
引理1.1[3]亚历山大多项式Δ(L)的3个基本性质:
(1)同痕不变量.
(2)拆接关系式:
(3)Δ()=1.
引理1.2[3]设L是纽结的任意一个有向投影图,则都有一个关于t的整系数多项式V(L),同时满足下面3个性质:
(1)它是同痕不变量.
(2)满足拆接关系式:

(3)平凡纽结的多项式为
V()=1.

则称V(L)是L的琼斯多项式.
1.3 排叉结
定义1.4排叉结p(c1,c2,…,cn)由n元数组(c1,c2,…,cn)确定,i=1,2,…,n(n≥3),|ci|表示该位置的半扭转数,ci的正负表示扭转数的正负(见图2).
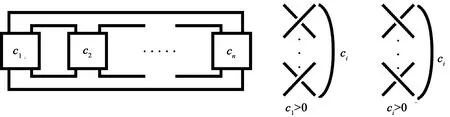
图2 p(c1,c2,…,cn)标准图
2 排叉结及排叉链环的琼斯多项式零点性质
引理2.1[7]当k是偶数时,P(k,1,…,1)为排叉纽结,其琼斯多项式为
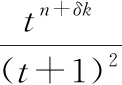
t1-n+(t+t-1+1)·(tk-1)·(-1)n-1}.
(1)
当k是奇数时,P(k,1,…,1)为排叉纽结,其琼斯多项式为
Vp(k(1),1(n-1))(t)=
(2)

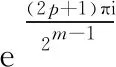
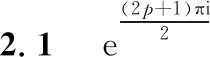


(tk+t+t-1+1)·t1-n+(t+t-1+1)·(tk-1)·(-1)n-1,
得到
(3)
根据i4k=1,i4k+1=i,i4k+2=-1,i4k+3=-i(k为整数),可以分下几种情况讨论(见表1,表2):

表1 取值讨论表

表2 取值讨论表
当k为偶数,n为偶数时: 此时式(3)变为

同样以下几种情况讨论:

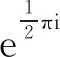
2.2 排叉链环P(k,k,k)的琼斯多项式零点性质
引理2.3[7]当k是正整数时,排叉链环P(k,k,k)的琼斯多项式为
(4)
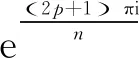
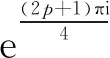

t3k+(t+t-1+1)[3tk+(-1)3k(t+t-1)],
得到
由数学归纳法知
循环重复取值,周期为8(见表3).

表3 取值讨论表
当k≠4n时,虚部不为0,结论成立.
当k=4n时,虚部为0,下面证明实部不为0.


表4 取值讨论表