基于变权-靶心贴近度模型的泥石流灾害影响下桥梁工程易损性评价
蔺 娅,李爱春,温海燕
(兰州交通大学土木工程学院,甘肃 兰州 730070)
泥石流灾害是我国山区最常见的地质灾害之一,具有极强的破坏性,常以冲击、冲刷等形式对附近的桥梁造成直接破坏,且淤积的泥石流还会造成河道的堵塞,引发水流冲毁桥梁的上部结构,对桥梁造成二次伤害,给周围地区经济发展和人民生命安全带来巨大的危害。近年来,国内外学者对于泥石流灾害影响下路基及桥隧工程的易损性分析进行了大量研究,如Eidsvig等[1]针对泥石流易损性评价中模型的不确定性,提出了采用损伤概率分布函数描述不确定性的方法对建筑物易损性进行评价;Kim等[2]考虑了自然环境、地质环境和人为破坏因素对泥石流灾害影响下桥梁工程易损性进行了评价,并制定了防灾综合规划方案;Liang等[3]利用数值方法模拟得到了泥石流对桥梁下部结构影响的易损性曲线,并进行了灾害预测及风险管理;徐士彬等[4]从泥石流作用效应和路基结构抗力两方面选取路基易损性评价指标,对路基易损性进行了评估,并证明了该方法的可行性;程杰[5]从泥石流发生的潜在危险性、桥梁的抗灾能力两个方面建立了山区桥梁建设期泥石流灾害风险评价指标体系,并运用模糊综合评价法对山区桥梁抗灾能力进行了评价,进而验证了该方法的可行性。
但上述研究主要关注泥石流灾害因素和工程体本身,未考虑其对社会经济以及人类活动的影响,且在评价指标赋权时,均是基于常权理论,未考虑到在实际情况中待评价指标权重在其状态值发生改变时也应随之变化。鉴于此,本文以受泥石流灾害影响下的桥梁工程为研究对象,首先选取易损性评价因素,建立了泥石流灾害影响下桥梁工程易损性评价指标体系;然后通过变权理论构造均衡函数确定评价指标的权重,并通过构造相关的关联函数求得靶心坐标,再利用靶心贴近度模型确定桥梁工程的易损性评价等级;最后以3座受泥石流灾害影响的桥梁为例,对其易损性进行了评价,以验证该方法的有效性与可行性,并通过结果分析得出对桥梁工程易损性影响较大的因素。
1 泥石流灾害影响下桥梁工程易损性评价指标体系建立
1.1 桥梁工程易损性的定义和分级标准
关于易损性定义的研究,目前还未有统一的定论,徐林荣等[6]在研究隧道工程易损性时将其定义为“由于自然灾害而导致工程体可能受到的损毁程度”;刘希林等[7]将“在一定区域和一定时间段内,由于泥石流灾害而可能导致的该区域内所存在的一切人力、财力、物力的潜在最大损失”作为泥石流易损度定义;潘小涛[8]提出易损性不仅包括承灾体遭受自然灾害的破坏和损害,还包括预见、处理、抵御灾害和从灾害中恢复的能力和特征。
在基于已有关于易损性定义的基础上,本文将桥梁工程遭受泥石流灾害的易损性定义为:在一定时间与空间内,由于受到泥石流灾害的影响而导致桥梁可能存在的受损程度以及从灾害中恢复的能力。根据本文对桥梁工程易损性的定义,结合目前人们对易损性分级标准的研究成果[9]以及桥梁工程遭受泥石流灾害的特征,考虑桥梁结构受损和功能受损两部分,将泥石流灾害影响下桥梁工程的易损性等级分为极高易损性、高度易损性、中度易损性、低度易损性、轻微易损性,并对其进行了描述,具体见表1。
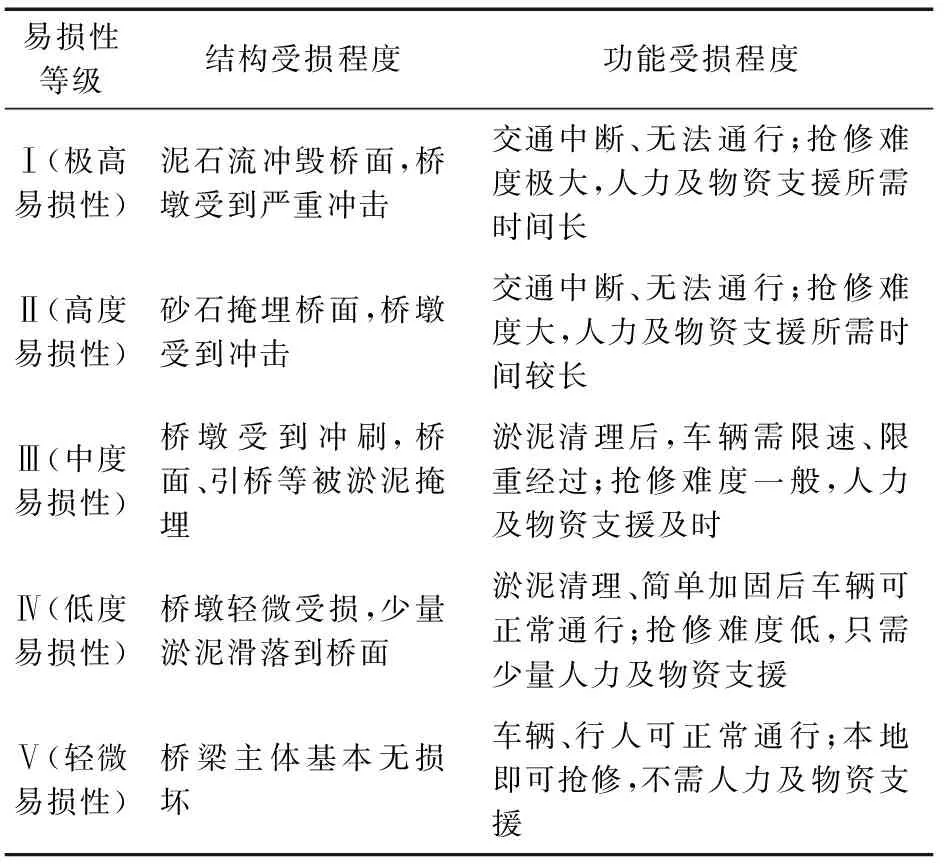
表1 泥石流灾害影响下桥梁工程易损性分级标准Table 1 Vulnerability classification standard for bridge engineering affected by debris flow disasters
1.2 泥石流灾害影响下桥梁工程易损性评价指标体系
根据上节关于桥梁工程遭受泥石流灾害的易损性定义,本文从桥梁抗灾能力B1、泥石流破坏能力B2、桥梁恢复能力B3三方面选取桥梁工程易损性评价指标。
由于桥梁跨径、桥梁跨数、桥下净空决定了桥梁受灾面积以及桥梁过流能力;桥梁受灾时其自身稳定性与墩基埋深、桥梁结构材料、桥梁防护情况息息相关;桥梁与沟道距离以及桥梁与沟道夹角决定了桥梁受泥石流冲击力度与於埋强度。因此,本文选取桥梁跨径C1、桥梁跨数C2、桥下净空C3、墩基埋深C4、桥墩结构材料C5、桥梁与沟道距离C6、桥梁与沟道夹角C7、桥梁防护情况C8作为桥梁抗灾能力B1的评价指标。
由于泥石流规模越大,对桥梁的损毁能力就越大;松散物源颗粒粗细程度会影响泥石流冲击力的大小,松散固体颗粒越粗大,冲击力就越强;泥石流流速、流深反映了泥石流的冲击力的大小;泥石流频次则反映了受灾频率;泥石流防治措施的好坏决定了泥石流对桥梁破坏程度大小。因此,本文选取泥石流规模C9、松散物源颗粒粗细程度C10、泥石流频次C11、泥石流流速C12、泥石流流深C13、泥石流防治措施C14作为泥石流破坏能力B2的评价指标。
由于桥梁养护的力度与桥梁恢复能力成正比;桥梁受损的严重程度决定了桥梁维修的难度大小;桥梁恢复正常的时间、恢复方式及成本是桥梁恢复能力的直观体现。因此,本文选取桥梁养护情况C15、桥梁受损情况C16、桥梁恢复正常的时间C17、桥梁恢复方式及成本C18作为桥梁恢复能力B3的评价指标。
根据以上确立的桥梁工程易损性评价指标及其相互关系,建立了泥石流灾害影响下桥梁工程易损性评价指标体系,见图1。

图1 泥石流灾害影响下桥梁工程的易损性评价指标体系Fig.1 Vulnerability evaluation index system of bridge engineering affected by debris flow disasters
1.3 易损性评价指标的量化分级标准
由于桥梁工程遭受泥石流灾害的易损性评价指标为定性描述指标与定量分析指标相结合,且均衡函数自变量的取值范围为0~1,因此在指标量化时,定性描述指标按照Ⅰ级([0.8,1.0))、Ⅱ级([0.6,0.8))、Ⅲ级([0.4,0.6))、Ⅳ级([0.2,0.4))、Ⅴ级 ([0,0.2))的对应关系进行专家打分,计算时取各专家打分的均值作为最终的量化结果;定量分析指标按照实测值采用线性内插法将其结果映射到[0,1]区间内。泥石流灾害影响下桥梁工程易损性评价指标的量化分级标准,见表2。

表2 泥石流灾害影响下桥梁工程易损性评价指标的量化分级标准Table 2 Quantitative classification standard of vulnerability evaluation index of bridge engineering affected by debris flow disasters
2 基于变权-靶心贴近度模型的泥石流灾害影响下桥梁工程易损性评价方法
2.1 评价指标常权权重的确定
本文采用向量夹角余弦法确定各评价指标的常权权重,其具体步骤如下[10]:
(1) 构造评价指标最优值向量S*和最差值向量s*。评价指标最优值向量S*和最差值向量s*的计算公式为
(1)
(2)
其中:
(3)
(4)
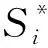
(2) 构造各评价对象与最优值向量和最差值向量的相对偏差矩阵R和Δ。评价对象与最优值向量和最差值向量的相对偏差矩阵R和Δ的计算公式为
(5)
(6)
式中:rij为第j个评价对象的第i个评价指标分值与最优评价值的相对偏差值;δij为第j个评价对象的第i个评价指标分值与第i个评价指标的最差评价值的相对偏差值。
(3) 确定评价指标的向量夹角余弦权重ci和常权向量W0评价指标的向量夹角余弦权重计算公式为
(7)

(8)
2.2 状态变权原理及评价指标变权权重的计算
为了避免利用常权理论计算得出的评价指标权重固定不变,从而对评价结果造成影响[11],在汪培庄教授[12]提出的变权思想的基础上,李洪兴教授[13]结合因素空间理论,提出了给因素状态加权的思想,称为状态变权。本文采用变权理论对求得的W0进行调整的过程如下:
(1) 均衡函数的构造。状态变权问题的关键在于确定合适的均衡函数[14]。在构造均衡函数时,通过确定具体的惩罚-激励状态分布来确定相应的分段函数S(x):
(9)
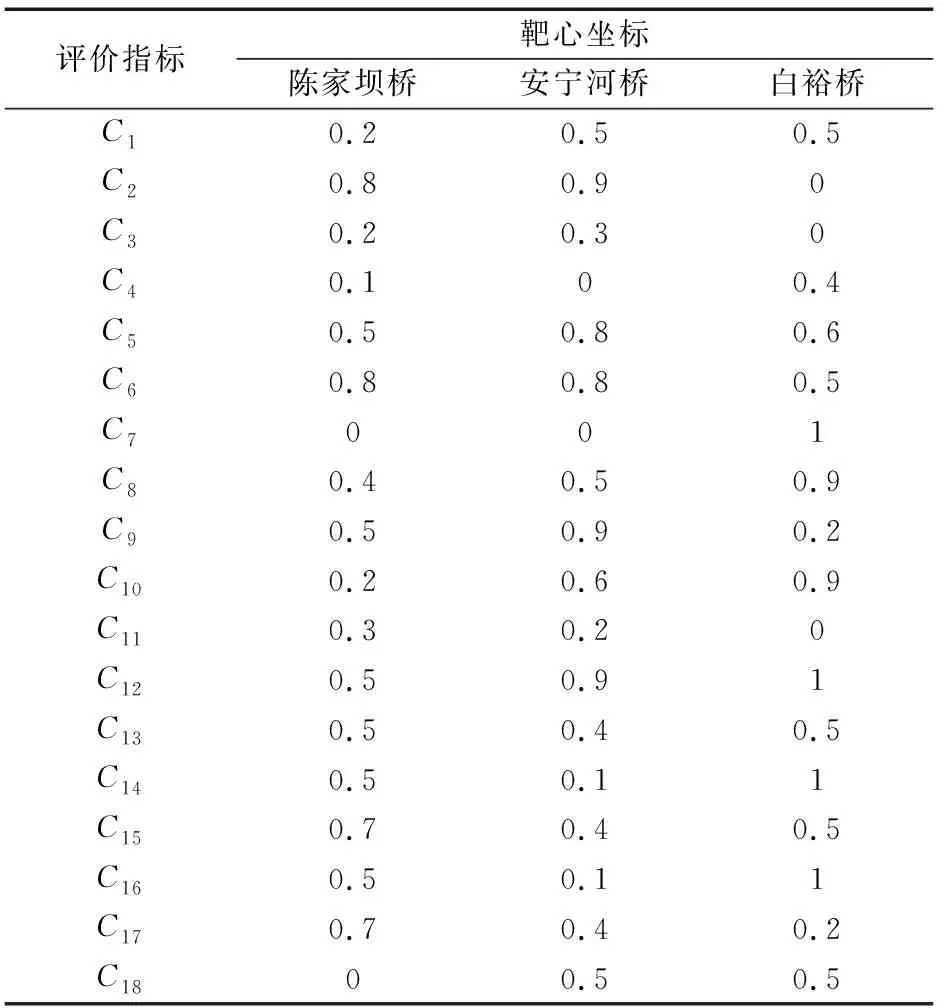
式中:C、c1、c2为评价策略,且0 (2) 确定评价指标的变权权重。由状态变权向量定义可知,评价指标的变权向量W是评价指标常权向量W0与状态变权向量S(x)的Hadamard乘积,即: (10) 在进行易损性等级评定时,会存在易损性评价指标评定等级不相容的情况:评价时需要从多个评价指标综合考虑,但会出现对一个易损性分级标准综合评定时各单项评价指标评定等级出现互相矛盾的情况,这一问题可以通过靶心贴近度模型来构造相应的关联函数得到有效地解决。 靶心贴近度模型的原理是通过构造一种单指标区间关联函数,将函数最大值作为待评价样本的靶心坐标,通过计算待评价样本对各评价类靶心的贴近度来对待评价样本进行等级分类[15]。具体流程如下: (1) 确定区间关联函数。设有m个评价样本,每个评价样本包含n个评价指标,记第i个样本在第j个评价指标下的属性值为xij。将所有样本分成p个评价类,则在第j个评价指标的取值区间内插入p-1个分点,将其分为以下p个子区间:[aj0,aj1],[aj1,aj2],…,[ajk-1,ajk],…,[ajp-1,ajp]。则第i个样本在第j个评价指标下关于第k个评价类区间[ajk-1,ajk]的关联函数为 (11) 关联函数值反映了评价指标属性值与分类区间中点之间的距离。关联函数值为正数,表示评价指标属性值在分类区间内;关联函数值为负数,表示评价指标属性值在分类区间外;关联函数值为0,表示评价指标属性值为分类区间的临界值。 (2) 计算靶心贴近度[16]。将上述单项评价指标对各区间关联函数值的最大值Yij作为易损性评价样本的靶心坐标,则第i个评价样本的靶心可以表示为:(Yi1,Yi2,…,Yin)。因此,设第i个评价样本关于第k个评价类的靶心贴近度为 (12) 式中:ωij为第i个评价样本关于第j个评价指标的权重。 本文以北川县陈家坝桥、冕宁县安宁河桥、宝鸡市白裕桥3座桥梁工程为例,利用本文提出的变权-靶心贴近度模型方法对其进行了泥石流灾害影响下桥梁工程易损性评价,并验证该方法的可行性。 根据自然环境、地质环境调查、灾情统计和致灾因素[17]分析,得到各桥梁工程概况见表3,并通过施工报告、现场测量、灾害报告获取定量指标数据,邀请专家对不同桥梁工程定性指标进行量化打分,最终采用插值法映射到[0,1]区间内,得到各评价指标的量化评分结果见表4。 表3 不同桥梁工程概况Table 3 Overview of different bridge projects 表4 不同桥梁工程各评价指标的量化评分结果Table 4 Quantitative score of various evaluation indexes of different bridge projects 将不同桥梁工程各评价指标的专家得分进行归一化处理,并代入公式(1)~(8)中进行计算,可得到不同桥梁工程各评价指标的常权权重,见表5。 表5 不同桥梁工程各评价指标常权权重和变权权重的计算结果Table 5 Calculation results of constant weight and variable weight of each evaluation index of different bridge engineering 3.3.1 均衡函数的构造 在构造均衡函数时,取μ=0.2、λ=0.4、α=0.6、β=0.8、C=0.3、c1=0.4、c2=0.5、K=2[18],由公式(9)可得状态变权函数为 (13) 3.3.2 评价指标变权权重的确定 根据表3和公式(13),可得出不同桥梁工程每一项评价指标的均衡函数值,并结合公式(10)和已求出的评价指标常权权重值,可计算得到不同桥梁工程各评价指标的变权权重,见表5。 根据公式(11)~(12),可计算得到3个桥梁工程分别对不同易损性评价等级的靶心坐标及靶心贴近度,并按照最大隶属度原则确定最终的易损性等级,其结果见表6和表7。 表6 不同桥梁工程靶心坐标的计算结果Table 6 Calculation results of bull’s eye coordinates 在2008年“9·24”暴雨作用下,原本在汶川特大地震中引起山体松动、滑坡的大沟里泥石流沟暴发中型泥石流,冲毁陈家坝桥,致使交通中断,且该地属于山中峡谷区域,受灾后原有小路被严重破坏,救援人员、机具进场困难。由表7可知,基于常权与变权计算确定的陈家坝桥易损性等级为Ⅰ级,属极高易损性,该评价结果与现场实际情况一致。 表7 不同桥梁工程靶心贴近度计算结果和易损性等级Table 7 Calculation results of bull’s eye closeness degree and vulnerability grades of different bridge engineering 2011年,安宁河桥在遭遇暴雨之后受到泥石流危害的影响,墩台基础遭受冲击,桥孔淤堵严重,但在受灾后有关部门对桥梁进行了及时修复与养护,包括清理桥孔、对墩台基础进行加固和清理桥面淤泥等,桥梁通行条件得到了基本恢复(见图2)。恢复桥梁通行条件后,通过采用限速、限载等手段在维持交通功能的同时避免了对桥梁造成二次伤害。由表8可知:基于常权计算确定的安宁河桥易损性等级为Ⅳ级,属低度易损性,该评价结果与淤泥清理、简单加固后,并采取限速、限载等手段限制通行的实际情况不符;而基于变权计算确定的安宁河桥易损性等级为Ⅲ级,属中度易损性,该评价结果与现场实际情况相符。 图2 安宁河桥清理加固后限速、限载通行Fig.2 Speed limit and load limit of Anning River Bridge after cleaning and strengthening 2005年,陇海线上建河—元龙间在遭受强降雨之后,K1346+570处暴发泥石流,白裕桥遭受泥石流冲击,1号桥墩基础局部冲空,2号桥墩受巨石撞击墩顶下沉,导致交通中断(见图3)。由表8可知:基于常权计算确定的白裕桥易损性等级为Ⅳ级,属低度易损性,该评价结果与交通中断、桥墩遭受强烈冲击的实际情况不符;而基于变权计算确定的白裕桥易损性等级为Ⅱ级,属高度易损性,该评价结果与现场实际情况相符。 图3 白裕桥桥墩因严重受损导致交通中断Fig.3 Traffic interruption caused by severely damaged piers of Baiyu Bridge 综上分析可知,基于变权计算确定的3座桥梁工程易损性等级的评价结果与现场实际灾情吻合,证明了构造的均衡函数与变权模型具有科学性、合理性,同时也证明了本文提出的基于变权-靶心贴近度模型的泥石流灾害影响下桥梁工程易损性评价具有可行性。 桥梁因遭受泥石流灾害而受损是多因素共同作用的结果,而由评价指标变权权重的计算结果可知,泥石流破坏能力因素在进行变权计算时都进行了强惩罚增加其权重,由此可看出泥石流破坏能力因素对泥石流灾害影响下桥梁工程易损性评价的重要性,据此可采取相应的防灾措施,以规避风险。 (1) 本文在分析桥梁工程易损性相关研究的基础上,综合考虑了在泥石流灾害影响下导致桥梁受损的多方面因素,并从桥梁抗灾能力、泥石流破坏能力、桥梁恢复能力三个角度出发,构建了泥石流灾害影响下桥梁工程易损性评价指标体系。 (2) 通过变权理论构造均衡函数,根据各评价指标的具体情况进行赋权,避免了评价指标相互中和,从而使评价结果更加客观、符合实际,同时也可以观察到同一桥梁工程实例中各评价指标的奖励或惩罚幅度,其结果具有横向对比性。此外,运用靶心贴近度法计算易损性贴近度,并确定易损性评价等级,其结果直观、可视,同时解决了评价指标之间互不相容的问题。 (3) 将变权理论与靶心贴近度法相结合应用于受泥石流灾害影响的桥梁工程实例易损性评价,并确定其易损性等级。结果表明:评价结果与实际灾情相符;且变权计算结果可反映出各影响因素的重要性,根据变权计算结果,可找出致灾性较强的因素,从而采取有针对性的整治措施。2.3 靶心贴近度模型的建立
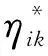
3 实例应用与分析
3.1 工程概况


3.2 评价指标常权权重的确定

3.3 评价指标变权权重的计算
3.4 靶心贴近度的计算
3.5 评价结果验证与分析



4 结 论

