基于高分子建材所探讨的一种新型结构分析方向
罗璐昕 徐家云


摘 要:以一种新型高分子材料所构成的组合结构案例为研究对象,提出一种将模型从整体最终拆分到特定面并用图论的方法来对数据间的关联进行整理与表达的新型结构分析方向。该方向可减少参数变更时有限元的计算次数,在一定程度上提高了各专业协同作业的效率;并且针对未来有可能参与到建筑中的各种新型材料提出了一种快捷高效的体系分析方法。
关键词:结构分析方向;高分子材料;图论;有限元
中图分类号:TU311 文献标识码:A
文章编号:1001-5922(2022)02-0137-04
随着科学技术的发展,人们需要更高效地建造出更大规模、造型更为复杂的建筑物。在建筑设计中,结构设计是其核心内容之一。其中的结构分析更是结构设计的重要内容,它要求计算结构在不同作用下的效应(如内力和位移)。现有的结构分析方法主要分为两种:一是对方程和边界条件等引入简化假设以得到简化状态的解;二是采用数值模拟技术求解。目前使用较为广泛的是有限元法。有限元法的基本思想是将求解区域划分为一系列仅由节点相连的单元,通过建立节点之间的平衡关系或能量关系方程式,再引入边界条件求解的方法[1]。
1 现有结构分析方法
随着研究领域的不断深入,现有的分析对象不仅仅局限于杆件,有限元法已逐渐由平面问题扩展到空间问题、板壳问题,由一开始的静力问题已延伸到电磁学、振动学等问题。于是,计算机带着各类有限元软件开始参与到模型建立及大型代数的计算之中,目前应用较为广泛的软件有ABAQUS、ADINA、MSC和ANSYS等[2]。但是,所有软件在进行有限元计算时的原则均是一致的:即先划定求解区域,再划分单元,抓取节点,引入边界条件,最后建立矩阵分析,用有限量逐步逼近去求解无限量。这种方式针对单一不变的结构而言,只需进行一次有限元计算,即可达到分析目的。但实际工程情况中,各专业间需协同作业,往往导致模型参数不停变更。按照现有的分析方法,每次发生重大变更时,系统需重新划分单元格再进行有限元计算,导致设计效率低下。同时,有限元法所得出结构调整的数据表达格式一般与其他专业难以直接兼容。所以,现有的结构分析方法暂时无法扩张到各专业的协同设计并完成较为高效的结构分析。
近年来,为了保证结构的安全性,工程上对结构分析提出了更高的要求。首先,传统的分析软件为了在精度上也要达到要求,往往需要进行成百上千次运算,所以结构的优化设计需要向着更快速的方向发展。其次,结构的性能不仅取决于其构件的性质,还取决于构件间的相对位置和连接。若单个构件发生的相对位移超限,整个结构体系的力学性质将会发生变化。因此,构件间的拓扑关系与其力学性质同等重要。图论是将矩阵代数和计算机科学紧密结合而发展起来的理论。它可将有限元的拓扑性贯通到图中,以一种连贯的数据表达形式来实现几何和力学上的数据贯通[3]。现已有一些研究团队利用图论对结构分析方法进行优化。例如,有学者结合图论方法,基于混合整数规划模型自动寻求峰/谷折痕的最优化分布形态,得到多折痕折纸结构创新构型[4]。
现有的结构分析手段主要是针对传统的结构建材,但针对一些新式的建材(如一些高分子材料[5])并没有可直接使用的结构分析方式。
本文基于图论的表达方法,针对符合要求的各类新型建材提出一种新型结构分析方法,即将模型从整体最终拆分到特定面并用图论的方法来对数据间的关联进行整理与表达。
2 简化图的分析方法
2.1 案例描述
本文使用的案例为一栋二层小型别墅(见图1),其中一层为左右对称两房间,中间为楼梯间;二层同样为对称结构,于单侧各设置3间房,投影与一层的单侧房间重合。方案的结构件设定为各向同性的高强高分子材质,纯榫卯结构连接。所用到的承重结构单元包括6类(柱、柱头、梁、楼板、墙板、楼梯),均由标准高分子构件组合而成。本文所涉及分析案例为梁柱连接节点。梁杆和柱杆的连接是通过3构件完成:梁两端为插接标准梁头,柱顶端为插接标准柱头,梁头和柱头通过榫卯嵌插连接,并通过梁销来固定(如图2所示)。
2.2 方法描述
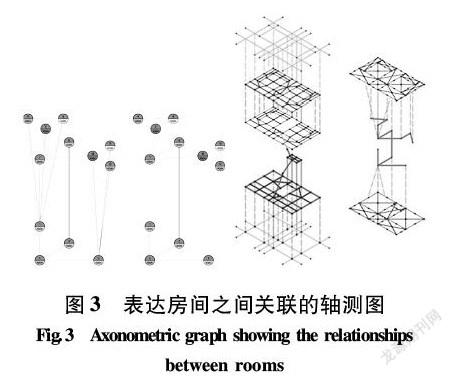
该结构分析方法立足于对建筑对象和其互相关联的处理和研究。将建筑模型中的各房间化为一节点,各相邻房间在空间上有直接关系则以直线相连,所得关联轴测图见图3。
房间在实质上是根据其功能要求由围护结构分隔出来的不同空间,这些围护结构就是各种类型的构件(墙、梁、板、柱)。假定整体建筑材料基本为均质且各向同性材料,现将每个构件简化为位于其几何中心的节点。节点之间的关联不僅代表构件之间几何及空间上的联系特征,也表征了应力的传递特点。例如,楼梯间顶板在几何上所承受荷载分别向周围7根梁传递,具体如图4所示。
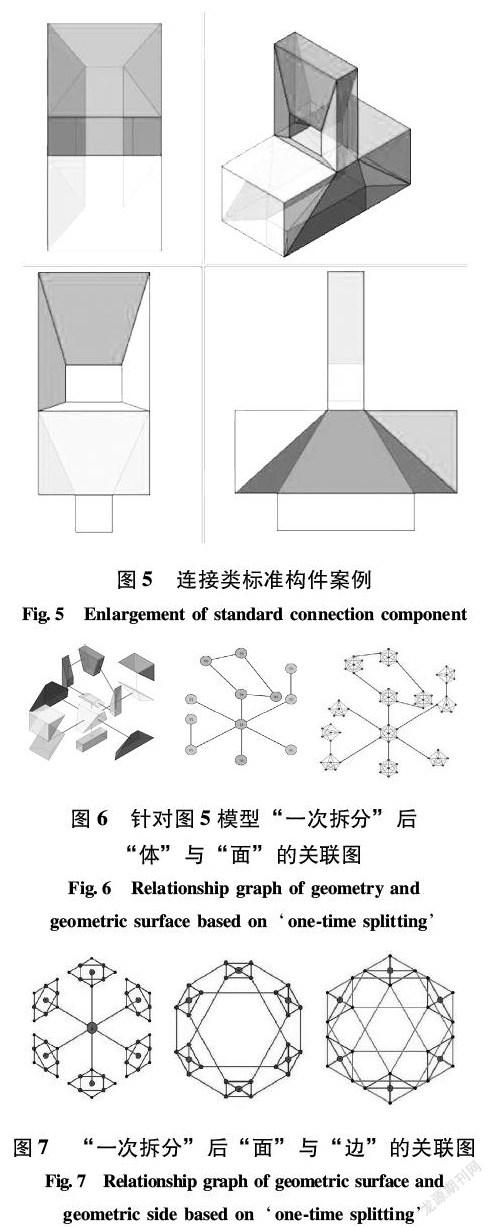
具体到构件层级,各类大型构件(墙梁板柱)及小型构件(连接节点)之间由于也有着相对标准的嵌插形式;具体如图5所示(一个标准的连接构件)。本方法中,将每个构件按一定原则拆解成由几何面包络而成的凸多面体组合,该过程命名为“对构件的一次拆分”。这些凸多面体体-面、面-面、面-边之间不仅在空间中具有严格的几何函数关系,在力学分析中的位移量也具备一定关联;这些关联可由节点的连接来表达;具体如图6、图7所示。
2.3 拆分规则描述
建筑模型实现从整体到房间,房间到构件,构件到凸多面体,最后由凸多面体到面的转化,都是基于“一次拆分”的方法。该方法的基本目标是将模型从整体造型拆分为各类将空间分隔开来的独立受力单元,其中凸多面体的面仅由三角面和四角面构成。整个拆分过程建立在单体均为凸几何体的假定上,拆分出的几何面囊括了所有在受力过程中由于几何突变而发生破坏的应力面及各种在可能受力状态下发生破坏的最大主应力面,这些面假定为该构件的概率破坏面。拆分基于两个原则:一是结构工程师基于经验判断出大概率发生破坏的应力面并完成一次划分,得到构件的凸多面体组合表达;二是通过直接进行有限元迭代来得到概率破坏曲面,以此构建凸多面体组合。在力学分析中,相邻“多面体节点”之间的关联可以用简化为二者的共用三角面或四角面的位移来表达,该种“面”位移可以直接由有限元计算出的“体”位移以几何函数关系划分到“面”;然后,再以图论的方法把该凸面体的几何数据和有限元计算的应力及位移数据进行整合并赋予表达。不论基于哪种原则进行“面”的划分,只要一次划分曲面能够“基本包含”概率破坏曲面(例如在设计荷载范围内,概率破坏曲面距离其最近的一次划分截面的距离小于一定值),则称该一次划分正确,即可得出:基于该材料或材料组合及其工艺所制作的构件在既定荷载设计范围内可以使用本结构分析方法进行分析。
2.4 新型结构分析法的特点
该方法将对建筑模型的研究转化成对一系列三角面和四角面几何关系及受力状态等问题的研究。建筑模型在需要改变某项参数时,现有方式一般为就新参数下的模型重新进行连续体的离散化,再重新建立刚度矩阵来进行有限元分析。而本文所述方法将符合要求的材料所制成的以标准结构嵌插形式组合而成的各类复杂建筑模型在整体上视为典型受力单元的组合。在拆分完成后完成从原始的建筑功能空间组合方案到既有的结构设计体系的数据贯通,即把构件之间的关联信息、几何体之间有限元计算得出的应力和位移信息、几何体与其几何面的函数关系进行整合及转化,基于图论的表达方法,得到幾何面参数及其应力位移的直接关联信息并计入数据库。在各专业按需变更参数时,直接调用数据库中的一次拆分图信息即可,以使协同作业更加高效便捷。从保证数据库的完整性出发,各专业的条件、假设和算法均可写入基于一次拆分图的数据结构中,并且后续,在一定范围内允许结构尺寸和框架组合调整的前提下,需高效地测试各类综合方案的各类工况模拟以更新数据信息。在后续的设计深化、设计变更和方案比选中,在一定的变更范围内,当需要进行结构安全复核时,不再需要模型进行重复的有限元验算操作,仅需在一次划分图上完成验算即可。
3 结语
在结构分析中引入一次划分概念和简化图方法,对结构体系进行从整体最终到标准面的拆解并对“面”之间的关系进行研究,将结构的数据以图论的方法与几何数据贯通;对部分在设计允许值(内力、变形)范围内的力学问题使用几何方法处理,减少参数变更时重复性的大规模计算次数,提高各专业间协同作业的效率。该方法也针对未来有可能参与到建筑中的各种新型材料提出了一种快捷高效的体系分析方法,基于该方法的多专业协同设计模块原型也已在测试中。
当然,上述方向的真正落地,依然需要建立在包括完备的有限元分析和力学试验体系下,逐步积累提高基于图结构的赋权函数的可靠性。同时也呼唤建筑领域对于潜在的各类新型结构承重建材的尝试。
【参考文献】
[1] 江克斌,屠义强,邵飞.结构分析有限元原理及ANSYS实现[M].北京:国防工业出版社,2005.
[2] KAVEH A.Computational structural analysis and finite element methods[M].[S.1.]:Computational Structural Analysis & Finite Element Methods,2013.
[3] 王亚军,王峰,李约翰.有限元分析系统在结构计算中的比较及展望[J].基建优化,2003(4):50-52.
[4] 陈耀,严嘉怡,冯健,等.一种非凸八边形四折痕折叠单元及可平折点的寻找方法[P].中国专利:CN110781565A,2020.
[5] 李波.一种三层方格两边为加厚直边的中空高分子建筑模板[P].中国专利:CN208803698U,2019.

