U型梁的剪力滞效应分析

杨勃 陈艳茹 张鹏

摘 要：以上海某轨道交通线延伸段U型梁1∶1静载试验为背景，借助Ansys有限元软件建立实体分析模型，并与实验所得数据对比，验证有限元模型的正确性。U型梁剪力滞效应的理论分析方法过于复杂和粗糙，为此利用有限元实体模型，分析U型梁段在跨中弯矩最大和近支座剪力最大两种车辆布置工况下，U型梁1/4跨、1/2跨和3/4跨的剪力滞效应。根据计算分析结果，提出了合理的修正方案。

关键词：U型梁;剪力滞效应;Ansys有限元分析;静载试验

中图分类号：TU311       文献标识码：A

文章编号：1001-5922（2022）02-0192-05

忽略剪力滞效应的影响，就会低估箱梁腹板和翼板交接处的挠度和应力，从而导致箱梁失稳或破坏事故的发生。桥梁梁体坍塌事故发生后，经过相关桥梁专家对这些桥梁的设计和计算方法的进一步研究和分析，发现这其中计算方法存在严重缺陷，设计时没有认真对待“剪力滞效应”带来的不利影响，致使实际应力大于设计应力，不能满足翼板承载力的要求而出现裂缝，进而导致应力过分集中造成桥梁的失稳和局部破坏。U型梁行车高度低、防噪声效果好、端面空间利用率高、综合造价低、能防止出轨车辆倾覆下落，给行走安全提供了必要保证，而且外型美观、视觉效果好，所以广泛应用于轨道交通之中[1]。但U型梁属于开口梁，整体性能差，荷载作用于梁底，使U型梁的剪力滞效应比较明显。

目前对U型梁剪力滞效应的研究不多，主要是借鉴张士铎教授提出的箱形薄壁梁剪力滞效应理论来分析。箱型梁属于闭口梁，与U型梁的受力特点不同，用箱形梁剪力滞效应理论分析U型梁的剪力滞效应存在一定的局限性。

本文提出了利用有限元程序分析U型梁剪力滞效应的实用方法，并将该方法应用于上海轨道交通八号线U型梁的剪力滞效应分析中，以检验该方法的适用性。

1 U型梁剪力滞理论分析方法

2 U型梁剪力滞效应的有限元程序分析方法

2.1 有限元分析方法简介

采用式（1）～式（4）计算剪力滞系数，因计算过于复杂，且误差较大，实际工程中使用不多[4]。本文提出的U型梁剪力滞效应分析方法，利用限元程序建立实体模型，求出计算截面底缘各点的应力值σx及其平均值σ0，借助于张士铎教授提出的剪力滞系数的概念，利用式（3）求出各计算截面下缘各点的剪力滞系数，以此研究U型梁计算截面处的剪力滞效应。以上海某轨道交通线延伸段U型梁的静载试验为工程背景，进行该方法的具体应用。

2.2 试验简介

本试验U型梁段，是上海某轨道交通线1∶1试验的模型。本试验是为了检验该U型梁段在设计荷载、开裂荷载、2倍设计荷载和2.5倍设计荷载分别作用下，U型梁的应力应变以及裂缝的展开情况，以验证结构的安全性和耐久性。该U型梁段为简支梁，净跨28.8 m，标准截面尺寸如图1所示。

预应力控制张拉力为1 300 MPa。按照规范计算预应力损失的方法计算，预应力损失为260 MPa。预应力筋两侧腹板各1根，底板8根，预应力筋布置如图1所示。车辆荷载轮载140 kN，考虑冲击系数后为165 kN，用钢锭块模拟。

2.3 有限元模型

U型梁的Ansys分析模型中，混凝土采用Solid45单元模拟，预应力筋采用Link8模拟。预应力筋的预加应力以Link8单元初应变的形式记入，泊松比取0.166 7。试验数据理论计算根据和模型实测吻合的很好。以下列出部分测点的应力数据，所选测点均为具有代表性的测点。1-H5表示U型梁端横梁下缘中心处的横向应力;2-H5表示1/4跨底板下缘中心横向应力;2-12#与2-16#表示1/4跨桥面板下缘纵向应力;3-3/4#表示中跨腹板上缘纵向应力;3-14#与3-15#表示中跨底板下缘纵向应力，结果如表1所示（负值表示压应力;正值表示拉应力）。

试验数据测点少，无法精确地分析U型梁的剪力滞效应。因此，本文采用有限元实体模型研究U型梁剪力滞效应。

以式（3）计算剪力滞系数，此处的σ0取U型梁底板下缘各点法向应力的平均值;σx取计算截面处各点法向应力的实际值。有限元模型单元的划分如图2所示。

2.4 不利工况分析

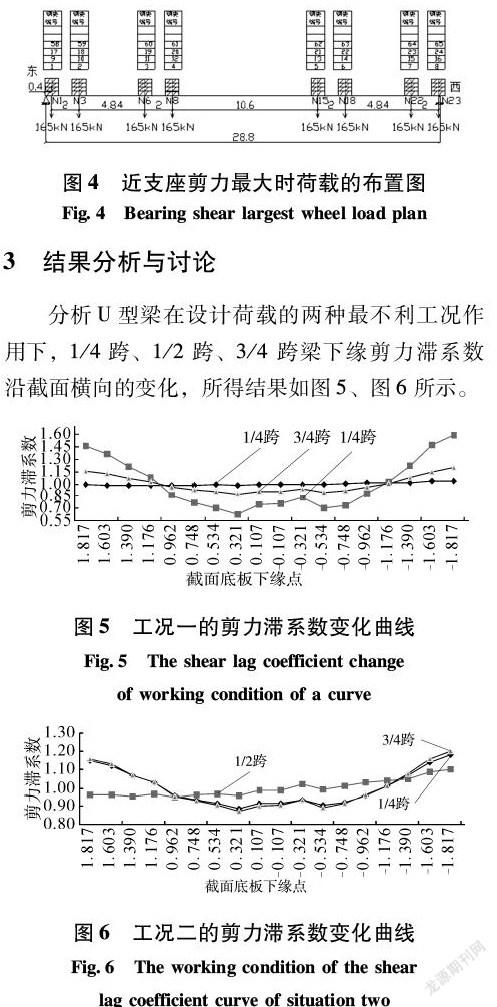
本试验分为两种最不利加载工况：工况一为梁段跨中弯矩最大时的加载工况;工况二为梁段近支点处剪力最大时的加载工况。两种工况下的车辆布置，如图3、图4所示。

3 结果分析与讨论

分析U型梁在设计荷载的两种最不利工况作用下，1/4跨、1/2跨、3/4跨梁下缘剪力滞系数沿截面横向的变化，所得结果如图5、图6所示。

由图5和图6可知，横坐标表示U型梁计算截面底板下缘点的坐标，纵坐标表示按照式（3）计算的该点剪力滞系数。如果不考虑剪力滞效应，计算截面处各点的剪力滞系数均为1。考虑剪力滞效应后，各点的剪力滞系数在1左右变化，沿截面呈现“U”字形的变化趋势。

（1）工况一：跨中剪力滞效应最为明显，下缘腹板处剪力滞系数达到1.59。3/4跨剪力滞系数最大为1.20，1/4跨剪力滞效应不明显;

（2）工况二：1/4跨和3/4跨均存在明显的剪力滞效应，且由于车辆荷载对称作用，两处剪力滞效应几乎相同。中跨剪力滞效应不明显;

（3）无论工况一和工况二，处于对称位置的剪力滞系数，左侧小于右侧;这是因为该U型梁段并非嚴格对称（如图1所示），在两种工况下，其发生了扭曲变形。对于工况一和工况二的剪力滞曲线在-0.534 m和0.321 m处均有明显下降，这是因为此处车辆荷载通过承轨台作用于U型梁上，形成集中荷载，影响了法向正应力的分布。

4 剪力滞效应处理及优化方案

4.1 底板厚度适当增加gzslib202204012333

例如板厚增加10%，板厚由0.23 m增厚到0.25 m，分析剪力滞系数变化的曲线如图7、图8所示。

由图7和图8可知，横坐标表示U型梁计算截面底板下缘点的坐标，纵坐标表示按照式（3）计算的该点剪力滞系数。考虑剪力滞效应后，各点的剪力滞系数在“1”左右变化，沿截面呈现“U”字形的变化趋势。

（1）工况一：跨中剪力滞效应最为明显，下缘腹板处剪力滞系数达到1.21，3/4跨剪力滞系数最大为1.01;1/4跨剪力滞效应略有降低。由图7和图8可以得出，板厚增加10%，在工况一条件下最大剪力滞系数从1.59，降低到1.21，同比降低23.9%。这说明增加底板板厚对跨中剪力滞效应明显;

（2）工况二：1/4跨和3/4跨均存在明显的剪力滞效应，通过增加板厚，剪力滞效应有一定程度的降低，从最大的1.2，减小至1.11，同比下降7.5%;1/2跨的剪力滞效应下降不多。

由此可见，通过增加U型梁的板厚可以有效降低剪力滞效应，所以，在工程应用中应适当提高底板的厚度。

4.2 腹板板厚增加、底板厚度不变的剪力滞系数变化曲线

腹板板厚增加10%，底板厚度不变的的情况下，剪力滞系数的变化曲线如图9、图10所示。

（1）工况一：跨中剪力滞效应最为明显，下缘腹板处剪力滞系数达到1.42，3/4跨剪力滞系数最大为0.99，1/4跨剪力滞效应略有降低。从图9和图10可以看出，板厚增加10%，工况一条件下最大剪力滞系数从1.59，降低到1.42，同比降低10.7%。这说明增加腹板板厚对跨中剪力滞效应有一定的影響;

（2）工况二：1/4跨和3/4跨均存在明显的剪力滞效应，通过增加腹板板厚，剪力滞效应有一定降低，从最大的1.20，减小至0.998，同比下降16.8%;1/2跨的剪力滞效应有一点下降。

4.3 工程应用

由此可见，通过增加U型梁的板厚可以有效降低剪力滞效应，考虑到两侧腹板截面远大于底板截面，增加腹板厚度成本较高，而且对剪力滞效应不是很明显。提高底板厚度，增加了底板截面面积，提高了截面惯性矩，进而提高了刚度，这可以显著降低剪力滞效应的影响。所以，在实际应用中，设计人员可通过适当提高底板的厚度来降低剪力滞效应的危害。

5 结语

就上海某轨道交通线延伸段U型梁1∶1静载试验段在设计荷载作用下的剪力滞效应，采用了本文提出的基于有限元方法的U型梁的剪力滞效应实用分析方法，对其跨中最大弯矩和近支座最大剪力两种工况进行了分析。

（1）该U型梁在上述两种工况下均存在明显的剪力滞效应，而且在第一种工况下，跨中的剪力滞系数达到1.59。然而在3/4跨和1/4跨时剪力滞系数小，相对应剪力滞效应比较弱;

（2）通过增加底板厚度比增加腹板厚度对惯性矩的提升效果明显，进而U型梁刚度提升较大;

（3）通过增加底板厚度和腹板厚度后剪力系数的数据对比分析可知，在设计时提高U型梁底板的厚度，这样可以高效增加U型梁刚度，对其减少剪力滞效应的效果较好。

【参考文献】

[1] 蒋朝文，张继文.细晶高强钢筋混凝土梁柱组合体非线性有限元分析[J].工业建筑，2009，39（11）：40-44.

[2] 张士铎，邓小华，王文州.箱形薄壁梁剪力滞效应[M].北京：人民交通出版社，1998.

[3] 李国平.预应力混凝土结构设计原理[M].北京：人民交通出版社，2002.