一种基于时空特征的短时交通流量交互预测方法

孙宝华 谢生曼 杨刚*

（1.中国瑞林工程技术股份有限公司 江西省南昌市 330036）

（2.华东交通大学电气与自动化工程学院 江西省南昌市 330013）

1 引言

交通拥堵是当前世界各地均面临的一个问题，不仅影响人们的出行，同时对环境和经济也有一定的负面影响，而智能交通系统（Intelligent Transportation System,ITS）的设计和使用则可在一定程度上实现交通诱导和控制，减轻或避免交通拥堵。自20世纪80年代以来，交通流预测[1]就一直是ITS 的重要组成部分，可根据历史和当前的交通流数据对未来时刻的交通流进行预测，其实现的技术也由原来的经典统计方法演化至数据驱动方法[2]。

交通流具有高度的非线性、不确定性、时间相关性等特点，当前时刻及历史时刻的交通状态特征信息直接影响着未来时刻的交通状态，而天气因素、节假日、重大事件等因素对未来时刻的交通预测也有重要影响。根据时间尺度的不同，其预测分为长时(long-term)和短时(short-term)预测[3]两类。其中，对未来15 分钟以内的交通状况所做的预测是微观意义上的，是交通预测研究的重要领域。Lippi 等[4]通过对短时交通流预测方法的分析总结，将其划分为时间序列预测和监督学习两大类。基于统计的交通流预测方法主要有差分自回归移动平均模型 (Autoregressive Integrated Moving Average Model，ARIMA)[5]、卡尔曼滤波 (Kalman Filtering)[6]、参数回归模型(Parametic Regressive Model)[7]和马尔科夫链（Markov Chain）[8]等。这类方法对于对非线性的数据集表征效果差，在识别复杂的模式上也不是很理想。基于数据驱动的交通流量预测主要有贝叶斯网络（Bayesian Networks）[9]、K 近邻（K-Nearest Neighbor，KNN）[10]、支持向量机（Support Vector Machine，SVM）[11-12]和神经网络模型（Neural Network Model）[13]以及神经网络的组合预测模型等。神经网络是一种受生物学启发的数学建模技术，由于其强大的学习能力，早在二十世纪八十年代，国内外学者就将其应用于交通流预测[14]。随着人工智能技术的发展，特别是深度学习、宽度学习系统的研究，神经网络为基础的交通流预测研究成为热点。文献[15]将RBF 神经网络应用于交通流预测；Zou 等人[16]等提出了运用长短期记忆神经网络（Long Short-Term Memory Networks,LSTM）进行交通流预测，具有长时记忆功能，解决长序列依赖问题；文献[17]通过构建门控循环单元（Gated Recurrent Unit,GRU）对交通流进行预测，其结构比LSTM 少了一个门单元，因此提升了学习效率。Byeonghyeop 等人[18]将图卷积神经网络（Graph Convolutional Neural Network,GCN）应用于数据预测领域，通过捕捉时序数据的时空特征提升预测性能。文献[19]结合了卷积和循环神经网络的优点设计了Conv-LSTM 网络，有助于数据时空特征的提取，保证预测效果。

一般情况下，单一预测方法对数据特征的挖掘不充分，因此，组合预测方法研究收到了广泛关注。文献[20]结合LSTM 和ARIMA 进行组合预测，Wang 等[21]将ARIMA 模型与RBF 网络相结合预测交通流，该方法对实际流量有较好的拟合度，优于传统回归预测方法和单一的神经网络预测模型；Wu 等[22]利用CNN 挖掘交通数据的空间依赖关系，使用LSTM 神经网络提取数据的时间特征，并使用多尺度建模对交通流进行预测。

实际上，交通流不仅受人们出行规律影响显示出一定的周期性，而各个观测点交通流之间还存在空间相关性。例如，某一节点交通流的突变，经过一定时间的传导，会延迟性地影响着上下游的交通状态，即交通流不仅存在时间依赖性，还有着空间关联性。兼顾交通流量时空特征的预测方法可以将时间相关性和空间相关性单独提取之后再进行特征融合，也可以将空间相关性的结果作为时间相关性分析的组成。其中，以LSTM 为基础的预测方法成为一个主要方向。

为解决实现短时交通流量的精准预测，本文借助LSTM的时序预测方面的优势，设计了基于交通流量时空特征融合的交互预测方法，通过空间特征分析和时间特征分析，实现交通流量的交互预测。其中，为了提高预测精度，设计了基于参数优化的LSTM 时序预测方法。

2 问题分析及系统设计

2.1 交通流量数据分析

图1b）所示为英国某A 类（A Routes）道路和高速公路（Motorways）交汇区域上下游的测量站点分布。根据站点空间分布，选择其中的13 个站点交通流量数据进行分析。某站点2019年7月1日-31日的交通流量数据如图1a）所示，为每间隔15 分钟统计的交通流量。其中，部分缺失的数据根据该站点上下游同时段数据的平均值进行填补。由图1a）可以发现交通流数据具有明显的非线性和周期性特点，工作日和周末的流量有明显区别，但相同时段的交通流量变化情况趋同。同一时间段内某站点上下游站点的交通流量变化情况如图1c）所示，表明上下游交通流量之间存在这一定的空间延迟传导特点，该站点的交通流量数据受到上游交通流量的变化而变化，同时经过一段时间后影响下游的交通流量数据，因此交通流数据具有一定的空间依赖性。

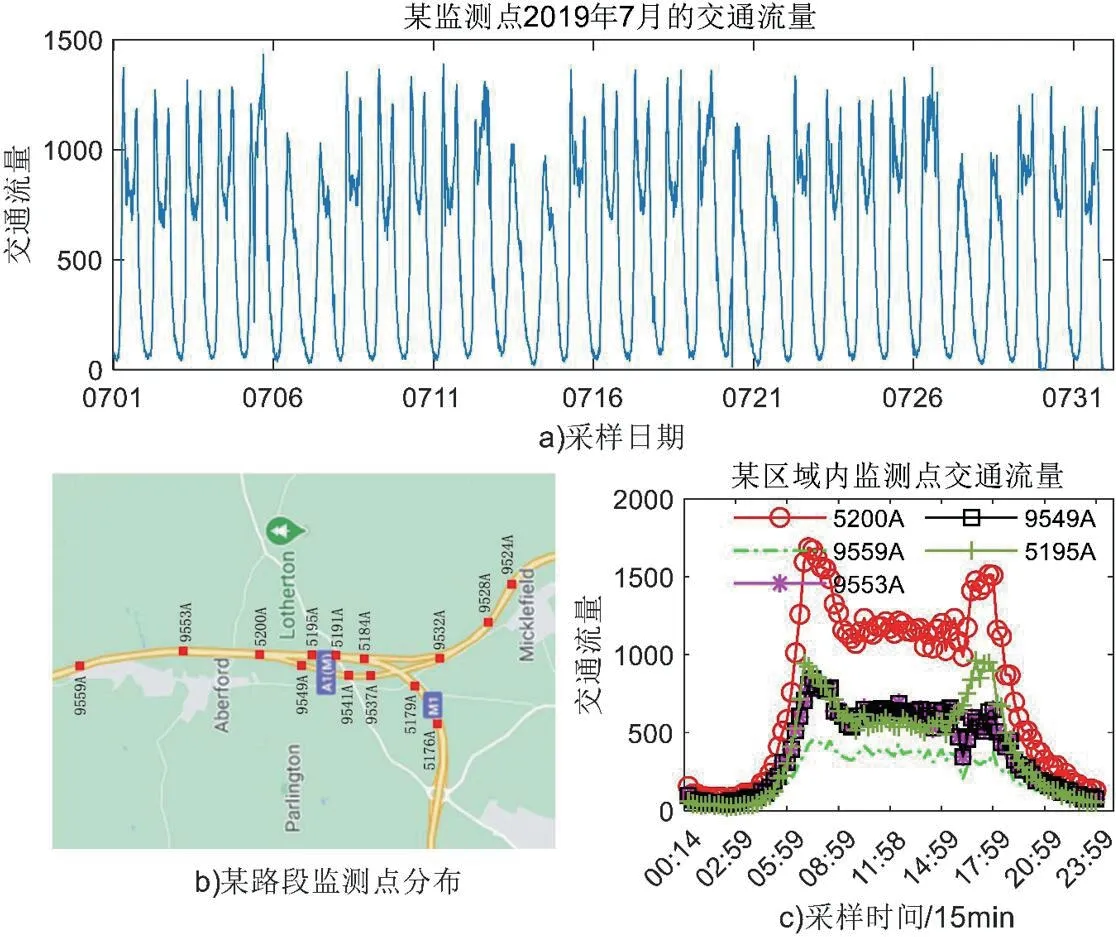
图1：英国某路段某区域监测点分布及交通流量

2.2 测量站点间的关联性分析

为了准确分析选定区域内各测量站点交通流量数据之间的空间相关性，采用空间距离（Distance）kD、最大互信息系数（MIC）kM对上述测量站点之间的关联性进行分析。

由于较短路段内的交通流量波动较小，因此选择的监测站点之间要达到一定的距离，即kD达到一定的阈值之后再考虑之间的关联性。最大互信息系数MIC 可反映两个线性或非线性变量之间的相关程度，因此可作为检测点之间空间相关性的判断依据。对于图1b）所示的监测站点之间的MIC 分析，将变量Xi和Yi视为图D 上的横纵坐标值，将横坐标的取值划分为x段，将横坐标的取值划分为y段。则MIC 值kM为：

其中，B表示x×y的网格G划分的最大值，B的大小设置是数据量的0.6 次方左右；MIC 的取值范围为[0,1]，数值越大表明该随机变量间的关联性较强；反之，关联性较弱。

为了充分分析监测站点之间的关联性，综合考虑空间距离和最大互信息系数，定义空间距离-最大互信息系数（Distance-MIC）联合指标kC判断站点之间的关联性。其中，图1b）区域内各站点之间的关联性如表1所示。

2.3 交互预测系统设计

一方面，基于空间特征的交通流预测部分根据2.2 节测量站点关联性分析，将表1所示的关联度较高的相关站点交通流量数据作为系统的输入，维数为12；将被研究站点的交通流量数据作为系统输出，维数为1。可得数学模型如下：

表1：选定区域内各站点之间的空间联系

其中，yd(n+k)=x(n+k)为系统输出，x(n)为相关监测站点采集的交通流量时间序列，k为预测步长。

另一方面，基于时间特征的交通流量预测部分则根据嵌入定理确定交通流量时间序列的延迟时间τ 和嵌入维数d，可得数学模型如下：

根据差分熵确定该站点交通流时间序列的延迟时间τ=7和嵌入维数d=4。令k=1，即实现系统的一步预测，对下一时间段内的车流量进行预测。

为了实现交通流的精准预测，设计了如图2所示的基于时空特征融合的交通流量交互预测系统通过分别对空间特征和时间特征的分析，实现了交通流量的交互预测。其中，为了提高预测精度，设计了基于TSO 参数优化的LSTM 时序预测方法，以及预计CNN-LSTM 的空间特征预测方法。

图2：基于时空特征融合的交互预测系统

LSTM(Long Short-Term Memory)[23]是循环神经网络(Recurrent Neutral Network,RNN)的一种改进，通过携带信息跨域的多个时间步的方法（单元状态C），实现较早时间步长的序列信息可以通过C传递到较后时间步长的细胞中来，这克服了短时记忆的影响，因此称为长短时记忆网络。LSTM 结构如图3所示，其中，黄色方框表示激活函数（σ为sigmoid 函数（0-1 之间），tanh 是tanh 函数（-1-1 之间）；粉色的圆内的“+、×、tanh”等表示向量之间的运算。LSTM 主要包括以下几个部分：

图3：LSTM 结构示意图

①单元状态（Cell State）：贯通LSTM 链式系统：

其中ft为遗忘门输出，通过选择遗忘确定计算Ct的Ct-1特征，it为输入门的输出，为单元状态更新值。

②遗忘门（Forget Gate）ft：对输入的信息进行选择性遗忘。T-1 时刻的状态h(t-1)和当前输入Xt与权值的计算并根据激活函数输出结果判断该输入信息是否应该保留，输出结果越接近1 越该保留，反之则该遗忘。

③输入门（Input Gate）it：类似于遗忘门，用于控制的哪些特征用来更新细胞状态Ct，可以看作是一个选择遗忘的过程：

④输出门（Output Gate）ot：根据前一个隐层状态ht-1和当前输入经激活函数得到ot；由此确定隐层状态ht。

3 实验仿真研究

3.1 数据说明

为了验证本文提出的融合时空特征的短时交通流交互预测方法性能，选择图1a）所示的某站点及其周围站点2019年7月的交通流量数据进行仿真研究。数据采样周期为15分钟，每天24 小时共计采集96 组样本，7月31 天共计2976 组样本。选择其中的80%用于训练，剩余的20%用于测试。数据经过图2所示的分析及处理，确定基于空间特征的预测和基于时间特征预测的模型输入分别为12 和4，输出维数为1。

3.2 参数选择

对于空间特征建模部分，采用CNN-LSTM 混合建模方法，相关参数根据经验进行选取。对于LSTM来说，隐含层数、学习率和迭代次数直接影响LSTM 的学习能力，因此为了提高基于时间序列的交通流量预测精度，采用模拟金枪鱼群合作觅食行为的金枪鱼群优化(Tuna swarm optimization,TSO)[24]算法对上述参数进行优化，优化流程入图2 中时间特征预测部分，受篇幅限制，此处不再赘述。

在基于时间特征的TSO-LSTM 交通流量预测部分，隐含层神经元为3，学习率0.08，迭代次数300。

3.3 实验结果及分析

为了全面衡量本文所提方法的性能，针对同样的样本，分别多次独立验证LSTM、SVM等方法的短时交通流量预测，并从均方根误差（RMSE）、平均绝对百分比误差（MAPE）、平均绝对误差（MAE）等几个方面进行性能对比。

图5：基于时间特征的交通流量预测（eRMSE=24.1298,eMAPE=1.2197,eMAE=19.7438）

图6：基于时空特征融合的交通流量交互预测（eRMSE=12.0670,eMAPE=0.4469,eMAE=15.3367）

MSE 是预测值和真实值对应误差平方和的均值，RMSE是MSE 的平方根，MAPE 是误差与真值比值的绝对值的均值，MAE 是预测值与真实值之间绝对误差的平均值。

其中，yi表示真实值，表示预测值，N为样本总数。上述三个性能指标的值越小，表明预测值与真实值越接近，系统性能也越好。

本文所做实验仿真研究均是基于Matlab 2021b 在Intel(R) Core(TM) i7-10510U CPU @ 1.80GHz 2.30 GHz，内存8 GB 的普通PC 机上进行的。为最大限度地消除随机因素对结果的影响，对于每一个仿真对象均独立运行50 次后取平均值。为便于计算，将样本归一化到[0，1]之间进行训练。设定最大迭代次数Tmax=2000，容许误差ε=1e-3。

基于空间特征的交通流量预测结果、训练过程，基于时间特征的交通流量预测结果、训练过程及数据融合交互预测结果分别如图4-6所示。

图4：基于空间特征的CNN-LSTM 交通流量预测（eRMSE=29.0684,eMAPE=2.3355,eMAE=31.1447）

本文设计的融合时空特征的交互预测方法与其他方法的性能对比如表2所示。由图4-6 及表2 可知，与其他方法对比，本文设计的交互预测方法的预测精度有了明显提升，性能由于单独的空间特征交通流预测和时间特征交通流预测。

表2：几种典型方法性能对比

4 结论

交通流具有典型的非线性、周期性和空间依赖性，具有时空特征。为了提高短时交通流量预测的精度，设计了一种融合交通流量时空特征的交互预测方法。首先，针对该区域内指定站点相邻站点之间的关联性，筛选关联性强的邻近站点交通流量作为该指定站点流量预测的空间特征构建LSTM预测模型；其次，结合交通流量的时序特征，根据指定站点的交通流量数据构建基于参数优化的LSTM 的时间序列预测模型；最后，综合考虑空间特征和时间特征的预测结构，作为交通流量预测输出。研究结果表明，时空特征融合交互的交通流预测方法有效提高了预测精度。