基于改进型遗传算法的强化学习特征选择方法
张坤 姚媛 蔡宇
(1.海军大连舰艇学院 辽宁省大连市 116000 2.63751 部队 陕西省西安市 710038)
(3.31455 部队 辽宁省沈阳市 110000)
1 引言
近年来,强化学习算法正广泛应用在电力分配、网络通信、机器人控制领域,其基本原理是通过智能体与环境不断的交互产生评价性的反馈信号,并利用反馈信号不断改善智能体的策略,最终使智能体能够自主学习到适应环境的最优策略[1-4],在与环境的互动过程中,选择何种特征作为模型输入是一个关键问题,特征选择不当不仅会导致算法性能下降,在实际问题中,也会导致更多的成本。无用的特征反而会干扰算法判断,因此必须非常慎重地选择状态特征。
目前,对于特征选择方面的研究主要包括三类:基于特征子集评价策略的特征选择算法[5-6]、基于搜索策略的特征选择算法[7-9]、基于不同监督信息的特征选择方法[10-12]。其中基于搜索策略的特征选择算法分为全局最优搜索策略、随机搜索策略以及序列搜索策略的特征选择算法。由于强化学习算法特征之间具有非线性关系,而且适应度函数计算耗时长,因此本文使用能兼顾效果和效率的基于随机搜索策略的特征选择方法。
2 基本思路
本文提出一种基于改进型遗传算法,使用PPO 算法作为适应度函数的特征选择方法,其中染色体为各特征的序列串,使用改进型遗传算法在特征空间进行搜索,将当前个体的特征作为PPO 算法的输入特征与环境进行互动,进而得出当前个体综合得分作为适应度值。由于强化学习算法训练时间较长,因此为了加速特征的选择,需要提前截断训练过程,同时保证对特征有效性进行一定程度的选择,综合以上因此,设计了本文算法,伪代码如下:

算法1 本文算法伪代码输入:17 种特征f1,f2,…f17超参数:种群数量 N最大迭代次数 T交叉概率 Pc 突变概率 Pm

输出:最优染色体序列 C 1 Q1 初始化,数量为N 2 使用适应度函数F 对Q1 进行评价,得到F(Q1,1)2 循环 t=2,3,…T 3 根据适应度选择父代染色体4 根据Pc 交叉染色体5 根据Pm 突变染色体6 更新种群7 使用F 对Qt 进行评价,得到F(Qt,t)8 对每个染色体的适应度进行标记9 结束10 返回 最优染色体序列 C
F(Q,t)为采用PPO 算法的适应度评价函数,本文使用种群迭代次数t 作为PPO 算法训练的次数,具体流程如下:

算法2 评价函数伪代码输入:染色体序列 Q种群迭代次数t超参数:minibatch size M actor number N hori:染色zon H输出体序列适应度F(Q,t)1 初始化模型参数 θ;3 循环 iteration=1,2,…t 4 循环 actor=1,2,…N 5 使用参数θ 与环境交互H 次6 计算Advantage 的估计 ,…,7 结束8 从NH 个样本中,选择M 次样本,其中M ≤NH,对θ进行更新9 θold ←θ 10 结束11 使用训练好的θ 和Q 进行测试,并返回适应度值F(Q,t)
本文主要完成以下工作:
(1)针对自回避行走问题中的寻路任务设计了17 种特征,包含感知特征、方位特征、状态特征、时间序列特征等。
(2)针对强化学习模型收敛速度慢的缺点,改进了遗传算法适应度函数,添加了准确和效率的平衡参数,加快了训练速度。
(3)通过将遗传算法应用在强化学习特征选择任务中,在不降低算法效果的基础上,将17 种特征缩减为5 种特征,减少了70.59%的特征数量,适应度提高了23.98%。
3 具体方法
3.1 场景构建
自回避行走(self-avoiding walk,简称SAW)指在一些格点内行走的路径,它们不重复经过任何一个点。本文使用贪吃蛇游戏作为算法运行场景,该游戏是自回避行走的一个特例,游戏过程中由agent 控制一条蛇的移动方向,并试图通过到达随机出现的目标点来增加自己的长度,同时使游戏变得越来越困难。游戏结束方式有3 种分别为蛇撞到自己或屏幕边界、距离上一次到达目标点超过25 步或者蛇身填充满屏幕。
3.2 特征工程
本文使用5*5 格子的贪吃蛇游戏环境,初始条件下蛇的长度为1,每次到达目标位置后蛇的长度增加1,并随机生成下一个目标点的位置。在一轮游戏当中,有效元素包括蛇头、蛇身、蛇尾、目标点、空白点、边界6 种。在不考虑元素相关性条件下,特征空间为65*5,因此如何有效的表示这6 种元素是本文讨论的重点。本文共设计了17 种状态特征,下面分别进行描述。
3.2.1 感知特征
感知特征表征环境的态势,有2 个分别为3 方向元素特征和8 方向元素特征。3 方向元素特征指以蛇头为中心探测前、左、右一格距离内是否为自身或者边界,如果有为1,没有为0,长度为3,如图1(a)所示。
8 方向元素特征指以蛇头为中心,分别探测前、左前,左、左后,后,右后,右,右前8 个方向直线上是否有边界、蛇身或蛇尾、目标点,其值为1/N,其中N 为距离元素的距离,没有元素值为0,长度为24,如图1(b)所示。
3.2.2 方位特征
方位特征表征目标或者蛇尾的方位,共5 个分别为目标方位、蛇尾方位、目标角度、目标相对方位、目标绝对方位。目标方位特征检测目标点相对于头部的位置,以头部为中心,分为4 个象限和2 条坐标轴共6 个位置,使用onehot 编码,长度为6。蛇尾方位与目标方位类似,只不过检测蛇尾相对于蛇头的位置,其余一致。目标角度检测目标相对蛇头的角度,公式为:R/360,其中R 为目标角度,特征长度为1,如图1(c)。
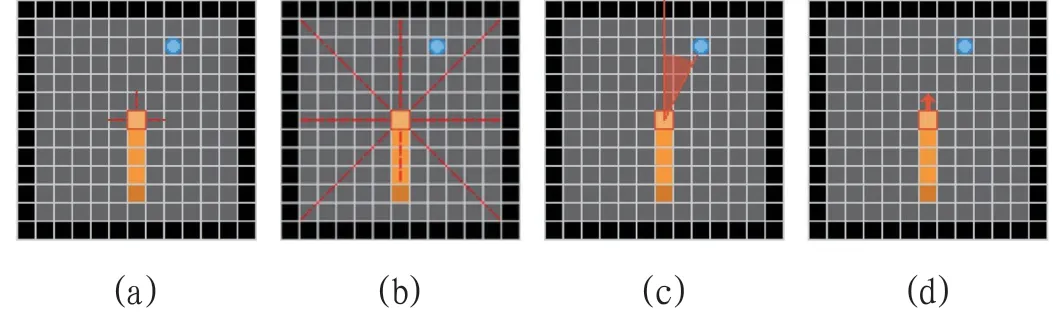
图1:特征示意图1
3.2.3 状态特征
状态特征表征agent 自身的状态,共3 个分别为自身方向、填充度、上步动作。自身方向特征使用1 维向量表示,检测头部方向,分为上下左右四个方向,使用onehot 编码,长度为4,如图1(d)。
3.2.4 标量时间序列特征
该特征将当前态势特征S0和上一步态势特征S-1叠加后生成新的特征,一同输入给下一步计算,对于向量特征,将S-1直接添加在S0的尾部,特征尺寸为原特征的2 倍。
3.2.5 S0矩阵特征
该类特征用矩阵的方式以蛇头作为中心描述S0时刻的态势,分为灰度特征、RGB 特征,6 层分解特征。灰度特征将蛇头、蛇身、蛇尾、目标点、空白点和边界表示在一个值为0 至1 的一维实数矩阵上,其中蛇头、蛇身、蛇尾值为0.7,目标点值为1,边界值为0.4,其余值为0,可以配合动态中心使用,特征尺寸为(sizex*sizey*1),如图2(a)(b)所示。
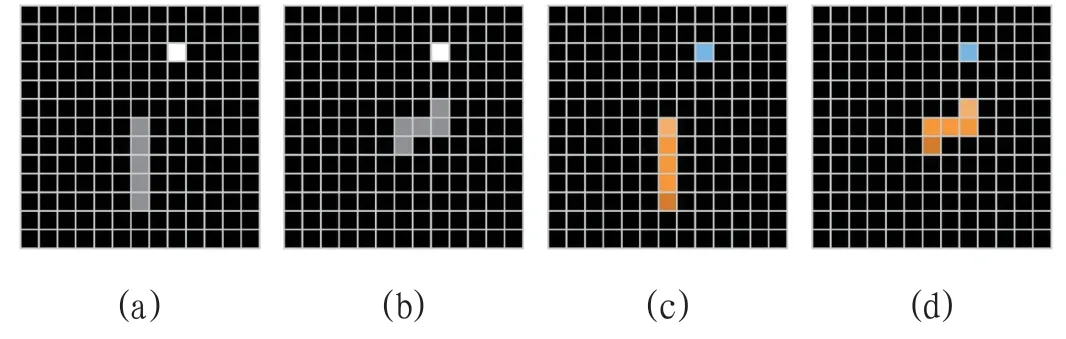
图2:特征示意图2
RGB 特征将6 种元素表示在一个值为0 至1 的三维实数矩阵上,其中不同部位使用不同的矩阵值,特征尺寸为(sizex*sizey*3),如图2(c)(d)所示。
6 层分解特征将蛇头、蛇身、蛇尾、目标点和边界表示在一个值为0 至1 的六维实数矩阵上,其中不同部位使用不同的矩阵值,保证在不同部位保持描绘在不同层上,如图3所示。
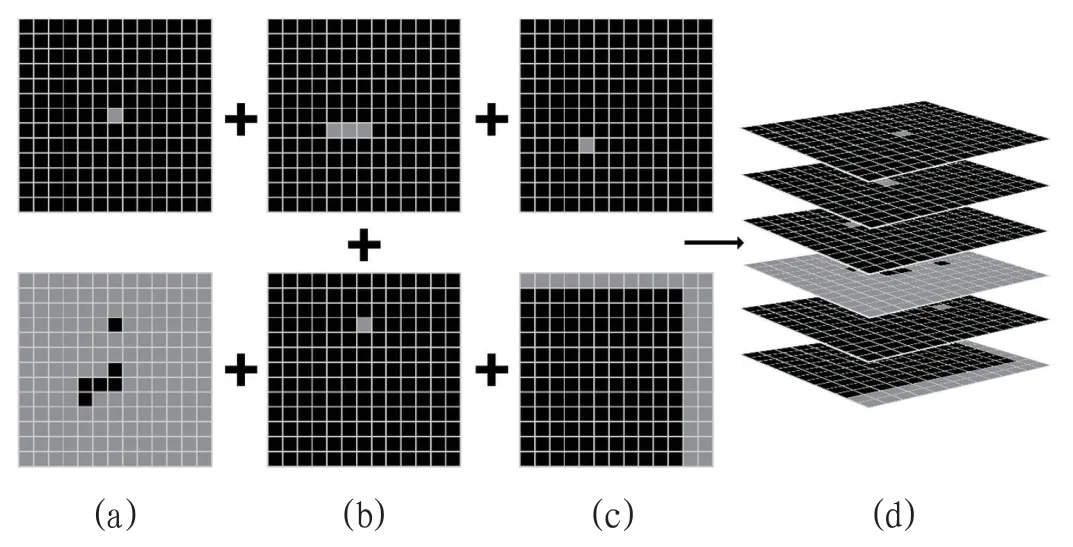
图3:特征示意图3
3.2.6 S-1矩阵特征
该类特征用矩阵的方式以蛇头作为中心描述S-1时刻的态势,同样分为灰度特征、RGB 特征,6 层分解特征3 类,其余与S0矩阵特征一致。
3.3 遗传算法的改进
在本文使用的硬件环境下,使用PPO 算法进行10000轮训练需要约30 分钟,则按照每次种群数量为20 计算,每代计算需要10 小时,如果进行20 轮计算,需要200 小时,这显然是无法接受的,因此针对强化学习算法收敛速度慢和缩减特征的目标,设计了如下适应度函数:
其中Nc(αt)表示当前参数C 进行αt 次训练获得的平均抵达次数,Mc表示当前参数C 的特征数量,这样可以保证训练前期更快的获得评价结果,后期获得更准确的评价结果。根据任务本身的难度,调节β 参数,从而对特征数量和算法表现进行平衡,获得适应当前任务的算法参数。本文α 设置为12.5,β 设置为0.5。
本文染色体编码长度为17,对应于是否使用17 个特征,形如[0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,1,1],如果对应位为1,则使用特征,如果对应位为0,则相应特征位置输入全0,这样可以保证PPO 算法使用的网络结构稳定,排除因网络结构引起的性能变化。
4 结果分析
本文共进行了20 轮改进型遗传算法的训练,初始染色体为[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],最优染色体为[1,0,0,0,0,1,1,0,0,0,0,0,1,1,0,0,0],具体的特征为(8 方向元素特征,3方向元素特征,目标角度,S0时刻RGB 特征,S0时刻6 层分解特征),每轮的最优适应度曲线如图4所示,每轮的特征数量如图5所示。

图4:最优适应度曲线

图5:特征数量曲线
经过20 轮训练后,得到可能的最优个体后,进行20000轮训练,并与使用全部特征的个体进行对比,训练结果如图6所示。

图6:最优染色体对比曲线
观察可知,最优染色体每轮平均抵达次数为23.25425,使用全部特征的染色体每轮平均抵达次数为23.5964,优化过的染色比原版染色体有1.47%的性能差距,这可以理解为算法的性能误差,但使用的特征数量减少了70.59%,最优染色体适应度为29.25425,比初始染色体适应度提高了23.98%。
5 结语
本文提出了一种基于改进型遗传算法的强化算法特征选择方法,将自回避行走中的寻路任务作为测试环境,设计了17 种特征,经过试验后发现,本文方法能够有效缩减特征数量,同时不降低算法性能,是一种行之有效的方法。但观察最优值可以发现,5 个最优特征有一定相关性,可能是一个局部最优值,下一步将继续研究如何利用特征相关性进一步提升算法表现。

