SV 波入射下饱和地层浅埋平行隧道动力响应机制＊

禹海涛 王治坤 陈峰军 刘中宪

1） 中国上海 200092 同济大学岩土及地下工程教育部重点实验室

2） 中国上海 200092 同济大学地下建筑与工程系

3） 中国上海 200080 上海建工集团股份有限公司

4） 中国天津 300384 天津城建大学天津市软土特性与工程环境重点实验室

引言

近年来随着我国交通领域的发展，新建铁路隧道与既有隧道间紧邻交叠的工程大量涌现，相邻隧道的存在将改变既有隧道的地层条件，从而造成既有隧道的地震响应特性发生改变.另外，地层与隧道群之间存在地震波的反射和散射等多种影响（李玉峰等，2015），对其结构的抗震安全性埋下隐患.因此，地层与隧道群间相互作用及抗震问题需引起重视.

目前，针对近邻隧道群的抗震研究已引起一部分研究人员的关注.Balendra 等（1984）采用波函数展开法，给出两个平行圆形地下隧道在简谐SH 波入射下的解析解；梁建文等（2004，2012）针对双线平行空洞地震响应问题分别采用解析解和数值解进行了研究并讨论间距的影响；Liu 和Wang （2012）基于复变函数法给出了全空间中双圆隧道对纵波和横波的动应力集中解析解；王国波等（2013，2015）针对紧邻多孔交叠盾构隧道工程问题，建立了土-隧道群相互作用计算模型进行了研究；Fang 等（2015）研究纵波作用下两圆形衬砌隧道的相互作用机制，并指出高频载荷将导致较低的动应力；Alielahi 和Adampira （2016）采用时域边界元法研究了双平行空洞对地表的地震动响应；Lin 等（2017）模拟了水平双隧道在垂直入射地震波作用下的二维动力响应，指出隧道间距和埋深是影响隧道地震响应的重要因素；Tsinidis（2018）给出了单双隧道的存在对地表地震动的响应，并指出地表结构的存在导致隧道变形和周围土压力响应增加.总体而言，目前近邻隧道的抗震研究通常针对单相介质场地，而在沿海地区地下水位较高，场地多呈饱和状态.相比之下饱和两相介质地层的动力特性更为复杂（李鹏等，2014），如孔隙流体的力学性质、孔隙流体与固相土骨架的耦合作用等，会直接影响饱和地层的动力特性，进而对隧道间动力相互作用产生影响，但目前对其影响机制研究尚不清晰.

本文旨在研究SV 波入射下饱和地层平行双线隧道动力响应的影响机制，基于Biot 饱和两相介质理论，采用间接边界积分方程法（Liuet al，2017）分别建立水平和竖向双线隧道动力作用分析模型，模拟SV 波垂直入射下饱和地层与平行隧道之间的动力相互作用，并分析双线隧道间距变化和SV 波入射频率变化对隧道结构地震响应及饱和地层孔隙水压力的影响规律.

1 模型及方法

1.1 计算模型

本文计算模型为饱和地层浅埋平行双线圆形隧道，如图1 所示.假设饱和地层为均匀各向同性多孔介质，衬砌为均质各向同性弹性体.双线隧道形式为水平分布和竖向分布，衬砌内外半径分别为r1和r2，埋深为d，双线隧道间距（圆心距离）为s.平面SV 波以θ角从基岩入射.假设行波方向垂直于隧道纵轴，即为饱和地层衬砌对平面SV 波的二维散射问题.

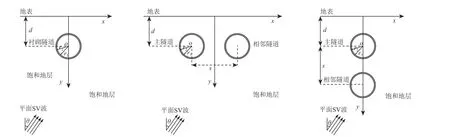
图1 计算模型Fig. 1 Calculation model

1.2 两相介质理论

根据饱和两相介质理论，采用Biot 动力控制方程中的u-w模型（Biot，1962），其各向同性多孔弹性介质的本构关系可以表示为

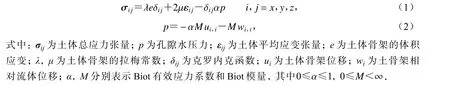
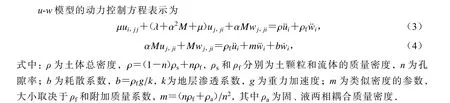
1.3 波场构造及求解

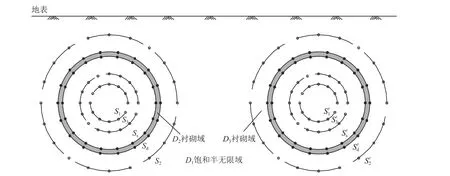
图2 波场构造示意图Fig. 2 Schematic diagram of wave field structure

式中：G，T，W分别表示饱和半无限域的位移、应力和流体相对位移格林函数；TT表示衬砌域的应力格林函数；b，c和d分别为虚拟波源面S1上P1，P2和SV 三种波源的源密度；e，f和g，h分别为虚拟波源面S2和S3上P1和SV 波的波源密度；上标′表示相邻隧道域，同理上述表达；uf，tf，wf分别表示自由场位移、应力和流体相对位移；上标（1），（2），（3）分别表示三个虚拟波源面S1，S2，S3；下标x，y分别表示x，y方向；下标1，2，3 分别表示P1，S，P2波.采用最小二乘法求解方程组从而得到虚拟波源密度；再与格林函数矩阵相乘，即可得到散射场中的结构应力和位移、流体位移和孔压；最后与自由场结果相加，即可得到弹性波入射下空间任一点响应的解答.

2 模型验证

由于饱和地层中平行双线隧道对弹性波的散射问题至今没有完全精确的解析解，现通过参数退化与现有单相介质条件下的动力响应对比来进行模型验证，即将孔隙率、流体体积模量和流体密度设为非常小，从而得到饱和两相介质退化为单相介质的计算结果.为了便于对比分析，首先定义无量纲频率，即通过散射体的特征尺寸和剪切波速vβ将频率归一化为

式中：a为散射体的特征尺寸（隧道半径）；ω为圆频率；λβ是剪切波的波长；η表示衬砌结构尺寸与地层介质中剪切波波长之比，η越大，则入射波波长越小，对应频率f越高.

首先，假设平行双线隧道无限远，同时衬砌和饱和半空间的模量与波数均相等，图3 给出了SV 波垂直入射下，隧道上方地表水平位移和竖向位移.定义位移无量纲幅值ui＝|Ux/Asv|，i＝x，y，表示地表位移与入射波幅值之比.隧道埋深d/r＝1.5 和5.0，黏滞阻尼比 ζ＝0.001，无量纲频率η，材料泊松比ν＝1/3.中可以看出，本文结果与解析解（Lucoet al， 1994）结果吻合良好.

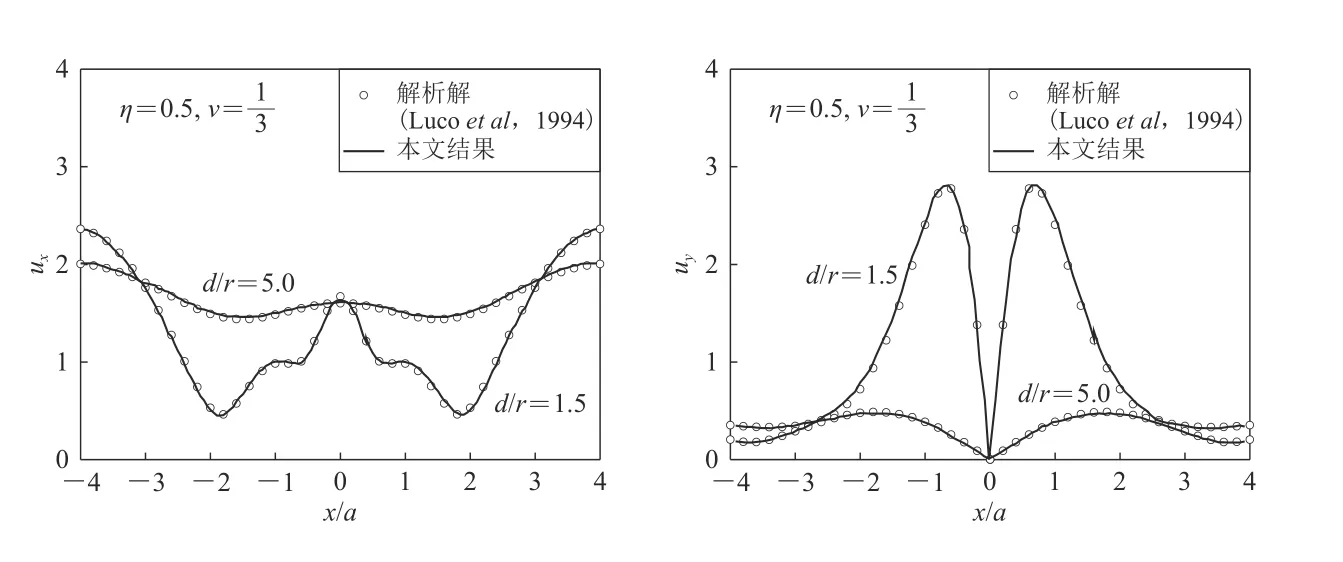
图3 地表水平（左）和竖向（右）位移幅值与解析解对比Fig. 3 Comparison of the horizontal （left） and vertical （right） displacement amplitudes of the surface with analytical solutions

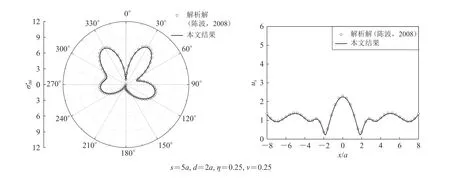
图4 本文环向应力（左）和地表位移幅值（右）与精确解对比Fig. 4 Comparison of the hoop stress （left） and surface displacement （right） in this paper with the exact solution

3 算例分析

本研究主要讨论饱和地层水平和竖向双线隧道在SV 波垂直入射下，隧道间距及SV 波入射频率变化对饱和地层-平行隧道的动力响应机制.双线隧道浅埋于饱和两相介质半空间中，衬砌内径取为3 m，外径取为3.3 m，深径比D＝d/a为3，d为隧道开挖断面的中心至地面的垂直距离.取饱和半空间介质材料参数，泊松比为ν1＝0.25，材料滞回阻尼比 ξ＝0.001（按照复阻尼理论引入，λ¯＝λ（1＋2ζi）， µ¯＝µ（1＋2ζi）），孔隙率n＝0.3，临界孔隙率ncr＝0.36，临界土体体积模量Kcr＝200 MPa，土颗粒体积模量Kg＝36 000 MPa，流体体积模量Kf＝2 000 MPa，土颗粒密度 ρg＝2 650 kg/m3，流体密度 ρf＝1 000 kg/m3.衬砌材料选取C40 混凝土，泊松比为ν2＝0.2，弹性模量E＝32 500 MPa，混凝土密度 ρ＝2 500 kg/m3.

下文参数分析中，定义双线隧道间距比S＝s/a，s为隧道断面中心之间的直线距离，选取隧道间距比S为3，5，8.考虑到地震波长若介于隧道尺寸的1—4 倍时，地震动响应会被明显放大（Hashashet al，2001），本文将选取无量纲入射频率η＝0.25，0.5，1.0 展开研究，即地震波长为隧道直径尺寸的4 倍，2 倍和1 倍.本文重点讨论饱和地层-平行双线隧道交界面不透水条件下隧道间距及入射频率变化对衬砌环向应力、地表位移幅值变化及周围地层孔隙水压力的响应规律，并以单条隧道分析结果为参照进行对比分析，揭示饱和地层-平行双线隧道的动力响应机制.

3.1 平行双线隧道地表位移响应

图5 水平双线隧道地表x （a）和y （b）方向无量纲位移幅值曲线Fig. 5 The amplitude curves of the ground x-direction （a） and y-direction （b）displacement of the horizontal twin tunnels

图6 给出了饱和地层竖向双线隧道地表x和y方向位移幅值曲线，x方向地表分布范围选取为x/a＝−10—10.可以看出：随入射频率的增加，地表位移响应特征发生显著变化.当频率较低（ η＝0.25，0.5）时，隧道间距的变化对地表位移响应影响明显，与单隧道相比，竖向双线隧道地表x向位移幅值减小，且随着隧道间距的增加，放大效应逐渐减弱，而y方向地表位移幅值随隧道间距的减小而增加，这是由于下层隧道的存在阻滞了SV 波的向上传播.当频率较高（ η＝1.0）时，隧道间距对隧道上方地表位移的响应影响较小，而远离隧道上方地表处的动力响应影响较大.

图6 竖向双线隧道地表x （a）和y （b）方向无量纲位移幅值曲线Fig. 6 The amplitude curves of the ground x-direction （a） and y-direction （b）displacement of the vertical twin tunnels

3.2 衬砌环向应力响应

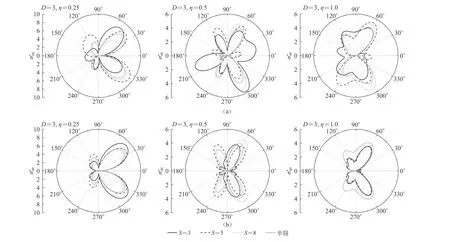
图7 水平双线隧道（a）和竖向双线隧道（b）的动应力集中因子 σ∗θθ幅值曲线Fig. 7 Amplitude curves of dynamic stress concentration factor of the horizontal twin tunnels （a） and the vertical twin tunnels （b）

3.3 平行隧道间距对周围地层孔隙水压力的影响

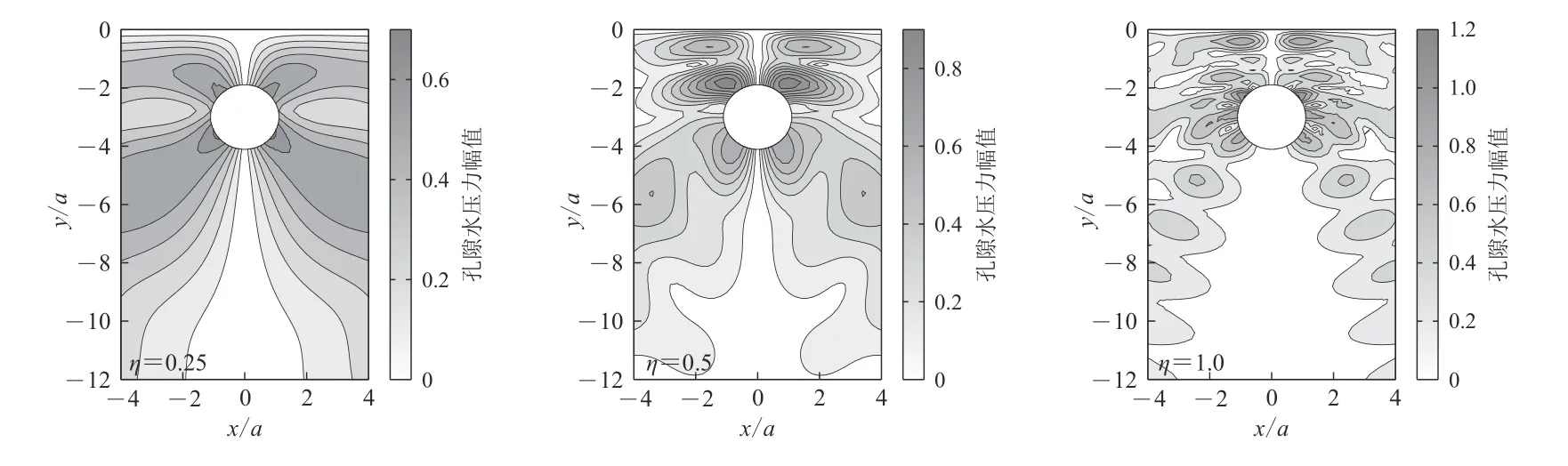
图8 不同频率入射下单隧道周围地层孔隙水压力分布图Fig. 8 Distribution of pore water pressure around a single tunnel under different incident frequencies

图9 给出了不同频率入射下水平双线隧道周围饱和地层孔隙水压力分布图，选取无量纲入射频率η＝0.25，0.5，1.0，隧道间距比S为3，5，8，分布范围选取为，x方向范围为−8—8，y方向范围为−8—0.可以看出，与单隧道相比，饱和地层孔隙水压力随入射频率变化规律基本一致，但由于水平相邻隧道的存在导致孔隙水压力峰值增大.当隧道间距比较小（S＝3）时且低频入射下，平行双线隧道周围孔压分布与单隧道分布相似，这是由于间距较小可近似将双线隧道视为一个整体.另外，当入射频率较低（η＝0.25，0.5）时，随隧道间距的增加，两隧道之间的区域孔隙水压力明显增加，这是由于地震波在隧道间的多次反射，导致两隧道之间区域出现明显的孔隙水压力集中.而当频率较高（η＝1.0）时，隧道间距对平行双线隧道的孔隙水压力影响不明显.

图9 不同频率入射下隧道间距比为3 （a），5 （b），8 （c）时水平双线隧道周围地层的孔隙水压力分布图Fig. 9 Distribution of pore water pressure in the formation around the horizontal twin tunnels under different incident frequencies for tunnel spacing ratio S＝3 （a），5 （b），8 （c）

图10 给出了不同频率入射下竖向双线隧道周围的孔隙水压力分布图，分布范围选取为，x方向范围为−4—4，y方向范围为0—−16.可以看出，与单隧道结果相比，竖向相邻隧道的存在对地层孔隙水压力的分布影响显著，且随着隧道间距的增加，隧道周围孔隙水压力峰值逐渐降低，当η＝0.25 时，随间距增加地层孔隙水压力峰值依次为1.6，1.0，0.6，而当S＝8 时，隧道间相互作用影响较小，两个隧道周围的孔隙水压力分布与单隧道近似一致.而较高频率入射下，随隧道间的距增加对周围孔隙水压力的影响范围增大而压力幅值变化不明显.

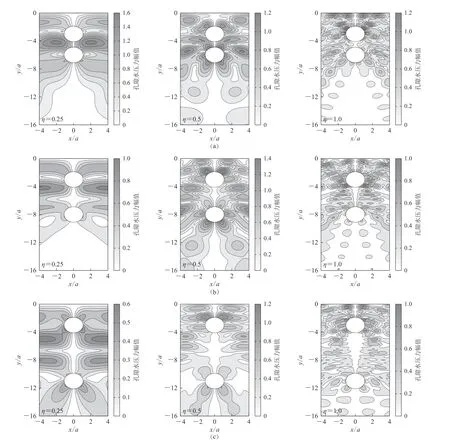
图10 不同频率入射下隧道间距比为3 （a），5 （b），8 （c）时竖向双线隧道周围地层的孔隙水压力分布图Fig. 10 Distribution of pore water pressure in the formation around the vertical twin tunnels under different incident frequencies for tunnel spacing ratio S＝3 （a），5 （b），8 （c）

4 结论

本文基于Biot 两相介质理论，采用间接边界积分方程法模拟SV 波垂直入射下饱和地层与浅埋平行双线隧道之间的动力相互作用，进而探讨了隧道间距及SV 波入射频率影响下，平行双线隧道结构及周围地层的动力响应机制，并以单条隧道分析结果为参照进行对比分析，得出以下结论：

1） 相比单条隧道，相邻隧道的存在改变了既有隧道结构和周围地层的动力响应特征，且动力响应幅值放大效应显著.

2） 平行双线隧道随间距的减小衬砌动力响应分布变化显著，且应力峰值逐渐增加.低频入射下水平双线隧道地表位移幅值和周围地层孔隙水压力随间距的减小逐渐增加，而高频入射下影响不太明显.另外双线隧道周围地层孔隙水压力分布明显集中在隧道之间的区域，且随着入射频率的增加孔隙水压力集中于隧道附近地层.

3） 水平双线隧道的动力响应特征与竖向双线隧道不同，且相比单隧道，水平与竖向双线隧道的孔隙水压力分布模式也不相同.随着相邻隧道间距的减小，水平双线隧道结构及周围地层的动力响应增加，而竖向相邻隧道的存在能阻滞SV 波向上传播，导致隧道及地表动力响应减弱.