混凝土结构可靠度的影响因素研究

陈振华 陈帆

湖州市规划设计研究院 浙江 湖州 313000

引言

在自然环境、使用环境和材料内部因素的作用下，随着钢筋混凝土结构进入老化期，其性能的劣化会导致抗力不断下降。这些使混凝土结构在规定的时间内、规定的条件下完成预定功能的能力降低，即混凝土结构的可靠度降低。在复杂的内外部环境影响下，钢筋混凝土结构在服役期间还会因为各种不同的原因产生不同的损伤，从而导致可靠度下降[1]。

目前，国内很多其他学者对混凝土结构可靠性进行了研究。王子晖等对在单一损伤情况下混凝土结构可靠度及大量对固后混凝土结构可靠度进行研究[1]。赵庆丽针对隧道衬砌正截面承载能力和正常使用性能对其进行了抗力时变和抗力时不变条件下的可靠度计算，提出了在役结构承载能力参数时变模型的调整方法[2]。但由于其可靠度计算的复杂性，很难应用到工程实际中。

本文结合前述论文中对混凝土结构的可靠度计算及分析并结合可靠度指标基本原理，探讨了各随机变量对可靠度指标的影响。

1 可靠度指标基本概念

1.1 H-L可靠度指标

结构失效概率可表达为：

引入可靠度指标β，其与失效概率Pf一一对应，可用来衡量结构的可靠度。对于服从正态分布或等效正态分布的功能函数，结构失效概率可表示为：

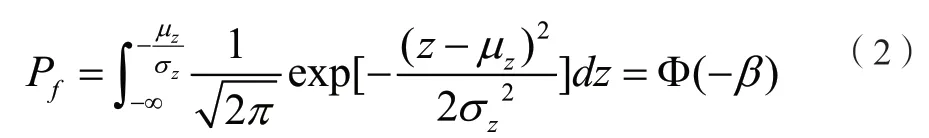
可靠度指标β可以经典地解释为，随机变量的标准正态空间内，均值点处到极限状态曲面的最小距离。

相关正态随机变量的H-L可靠度指标的矩阵形式为[2]：

或者，等效地，也可表示为：

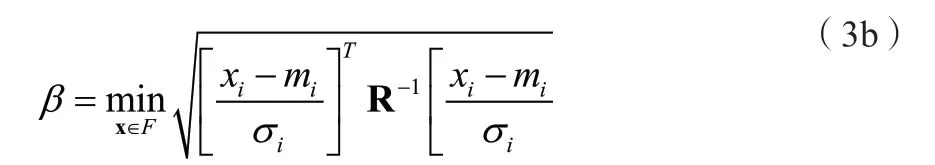
式中，X是随机变量xi集合的向量表示；是均值μi的向量表示；C是协方差矩阵；R是相关系数矩阵；iσ是相关系数矩阵；F是失效域。本文的可靠度计算更偏向于选取式3b，因为相关系数矩阵R的表示相对容易，且比协方差矩阵更直观。

2 混凝土结构可靠度影响因素

2.1 混凝土强度退化对可靠度的影响

混凝土结构受到混凝土碳化、钢筋锈蚀等各种环境因素的侵害，最终会引起耐久性损伤，主要表现为：钢筋有效截面减小和强度降低、混凝土截面损伤以及钢筋和混凝土间的黏结性能下降，导致结构承载能力逐步降低，直至小于外界荷载作用以致结构失效[3]。

本文以实测混凝土强度对强度准则功能函数的可靠度的影响是显而易见的[4]。假定实测衬砌混凝土强度的变异系数恒为20%，则图1表示可靠度指标及失效概率随实测混凝土强度均值的变化情况。

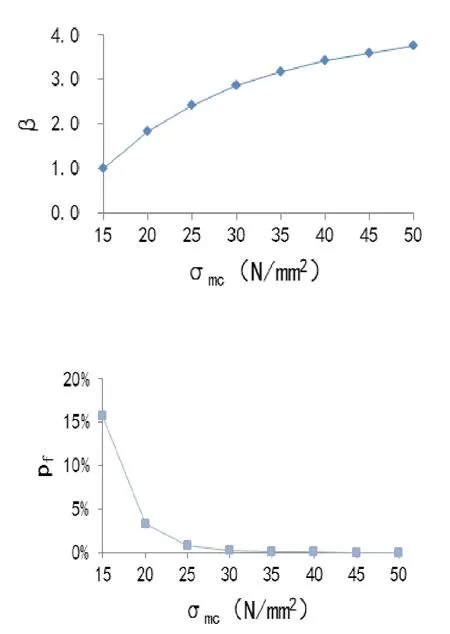
图1 实测混凝土强度均值与可靠度指标和失效概率的关系

可以看到，随着实测混凝土强度σmc的增加，可靠度指标β显著地随之变大，相应地，失效概率pf变小。当σmc等于10.7N/mm2时，pf为49.75%；而当σmc增加到35N/mm2时，pf快速地减小到0.016%。从工程的角度，当混凝土采用C40及以上的混凝土进行浇筑，设计可靠度较高；随着结构使用年限的增大，混凝土在环境因素影响下会不可避免地出现老化，进而导致其强度降低、强度变异性变大。所以，讨论实测混凝土强度有很大的意义。

2.2 相关系数对可靠度的影响

两个随机变量的相关系数取值在-1和1之间，在可靠度计算中可以设置相应的相关系数。以盾构隧道为例，地层抗力系数k和水平直径变形量δ是负相关的。为评估负相关系数对可靠度分析的影响，在实测衬砌混凝土强度δmc=30/mm2情况下，对不同的相关系数ρkδ计算可靠度指标β及失效概率pf，见图2。其中，ρkδ取负值。

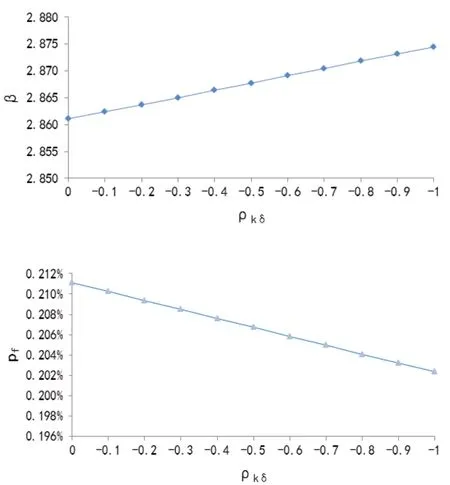
图2 随机变量相关系数 ρkδ与可靠度指标和失效概率的关系

可以看到，随着相关系数ρkδ的减小，可靠度指标β显著地随之变大，相应地，失效概率pf变小。当ρkδ等于0时，pf为0.211%；而当ρkδ等于-0.99时，pf减小到0.202%。所以，实测衬砌混凝土强度σmc=30MPa情况下，地层抗力系数和水平直径变形量的相关性对可靠度分析影响不大，而且假定它们的相关系数为零是偏于保守的。有时候从工程的角度，为简化分析，我们可以不对负相关的随机变量的相关性进行研究，而直接假定相关系数为零。

2.3 非正态分布随机变量可靠度的初步探讨

B.K.Low等建议，一般情况下，当一个随机变量的变异系数大于0.2时，应当用对数正态分布来代替正态分布以去除可靠性分析和Monte Carlo模拟中负值[5]。

同样，也可以用四个参数的有上下界的Beta分布来代替正态分布。Beta分布的均值μ和标准差σ可以用四个参数（α，λ，max，min）来表示：

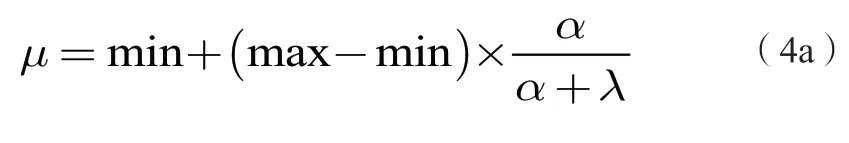
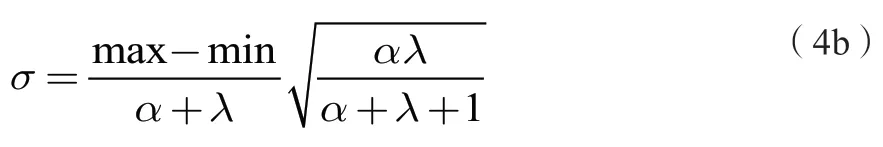
若假定变量区间为(μ-5σ,μ+5σ)，将最大值和最小值代入式8，可得α=λ=12。即Beta分布的四个参数为(12,12,μ-5σ,μ+5σ)。本文以盾构隧道为例，选取隧道埋深、水位高度、管片截面特性等作为确定性变量；实测混凝土强度smc，土重度g（假定土层为均匀土层），静止土压力系数K0，地层抗力系数k，水平直径变形量d这五个参数为相互独立的正态随机变量。所以三种不同分布情况下随机变量参数的取值见表1。

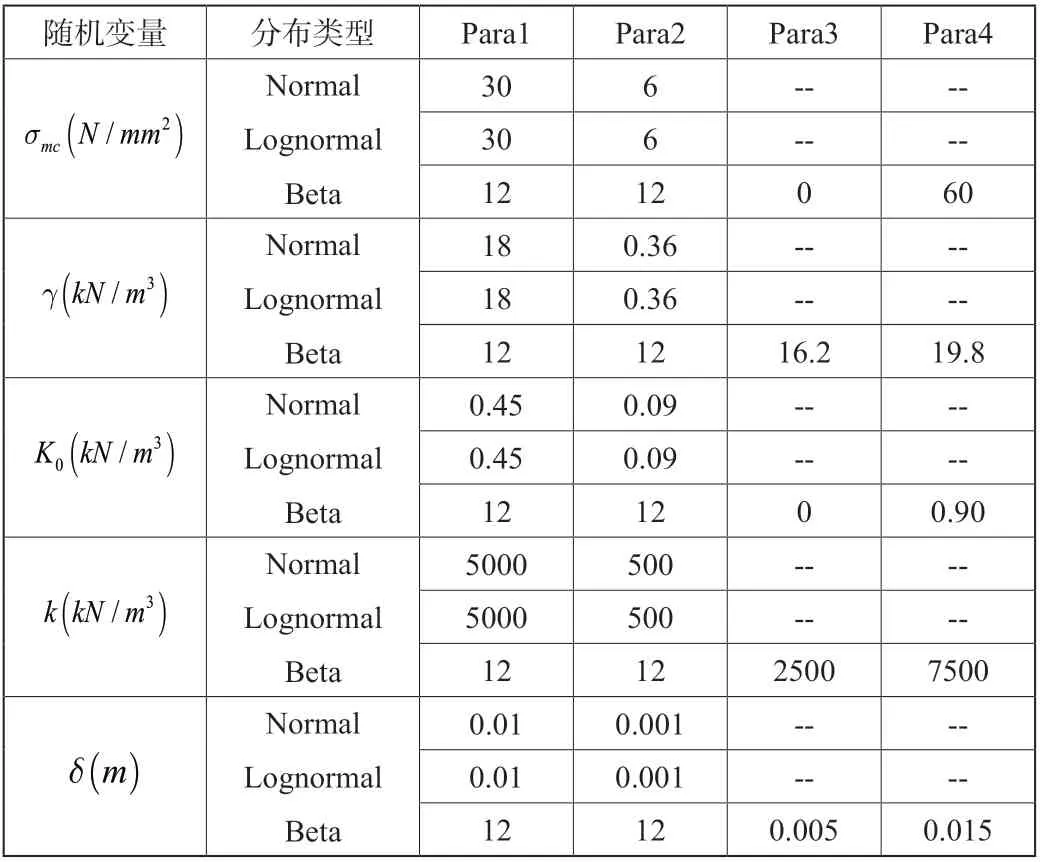
表1 三种不同分布类型的各随机变量参数取值

现分别研究本节涉及的五个随机变量分别为正态分布、指数正态分布和Beta分布时的概率密度函数，并进行比较。可知，随机变量的变异系数越大，对数正态分布曲线形态和正态分布曲线形态的差异越大；而Beta分布始终能较好地拟合正态分布曲线。此处对具体的随机变量进行展开。

若可靠度计算中采用的随机变量的概率密度函数不同，则相应的可靠度指标β和失效概率fp也不同，见表2。

表2 不同实测混凝土强度情况下，不同概率分布类型的可靠度指标和失效概率

3 结束语

本文结合前述论文中对混凝土结构的可靠度计算及分析并结合可靠度指标基本原理，探讨了各随机变量对可靠度指标的影响，主要结论如下：

随着混凝土结构使用的增大，混凝土在环境因素影响下会不可避免地出现老化，进而导致其强度降低、强度变异性变大。

实测混凝土强度对既有、结构可靠度影响较大。可靠性随着实测混凝土强度的增大而增大。讨论实测混凝土强度有很大的意义。

随机变量相关系数与可靠度指标及失效概率存在相关性。为简化分析，实际工程中常对负相关的随机变量相关系数假定为零。

随机变量的变异系数越大，对数正态分布曲线形态和正态分布曲线形态的差异越大；而Beta分布始终能较好地拟合正态分布曲线。