吸气式电推进中的气体捕集系统的设计分析
杨 超,胡 远,孙泉华,3,黄河激,3
(1. 中国科学院力学研究所空天飞行科技中心,北京 100190;2. 中国科学院力学研究所高温气体动力学国家重点实验室,北京 100190; 3. 中国科学院大学工程科学学院,北京 100049)
0 引 言
超低轨卫星(高度150~200 km附近)有着非常重要的军事及民用价值,但卫星飞行中遇到的大气阻力随着轨道高度的降低而显著增加,造成动力难以维持卫星的长时间服役,“留不住”成为超低轨卫星所面临的最大困难。吸气式电推进技术通过捕集轨道上的气体分子作为工质产生推力,不需要卫星携带推进工质,是一种非常有潜力的先进动力技术,有望突破超低轨道飞行器和卫星星座“留不住”这一技术瓶颈。
为了达到推阻平衡的基本要求,吸气式电推进需要满足如下关系式
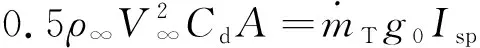
(1)
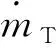
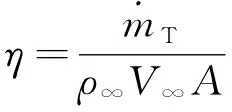
(2)
将其代入式(1)后可得
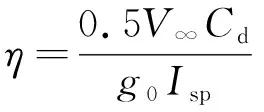
(3)
取=2,=7.8 km/s,则为1500 s和3000 s时满足推阻平衡的最低捕集率为52%和26%。
在150~200 km的轨道高度上,空气的分子平均自由程处于10~100 m的量级,气体捕集过程主要处于自由分子流域,分子间碰撞的影响非常微弱,气体捕集能力与分子和壁面的碰撞密切相关。研究表明,当气固相互作用为镜面反射时,气体捕集系统的长度、入口面积、出口面积、进气道型面等几何参数均对捕集率有明显影响。特别地,当进气道型面为抛物线旋成体时,经过优化后捕集率能够接近100%。而当气固相互作用为完全漫反射时,进气道长度、入口面积、出口面积等几何参数依然对捕集率有明显影响,但进气道型面对捕集率的影响明显减弱。例如当进气道型面为图1所示的斜线旋成体和抛物线旋成体时,捕集率差异并不大。

图1 气体捕集系统的进气道型面侧视图Fig.1 Side view of an air intake system
基于飞行数据反演的卫星阻力系数表明200 km以下的气固相互作用以漫反射为主,原因是低轨大气中的原子氧会吸附在固体表面从而影响分子在壁面的反射过程。因此,目前工程中主要基于漫反射模型来设计捕集系统。由于漫反射条件下进气道型面对捕集率影响不大,因此工程设计中大多将进气道型面简化为直线进气道并通过收缩段过渡至出口(下文称为直管构型捕集系统)。这种直管构型捕集系统的关键参数是进气道的无量纲管长(管长与基于直管截面的参考长度之比)和收缩段的面积收缩率(出口面积与入口面积之比)。以最大捕获率为目标的最优无量纲管长与无量纲来流速度有关,针对地球和火星轨道的优化结果一般处于5~10之间。实际设计中常将单一直管替换为相同无量纲管长下的一簇直管,即所谓的多孔准直器,主要目的是不改变捕集率的前提下缩短进气道管长,从而减小卫星侧壁面的阻力。面积收缩率对捕集率的影响则较为复杂,增大出口面积有利于到达捕集系统出口的分子进入下游的电推力器,但同时也增大了下游的中性和带电粒子回流至捕集系统的概率。在日本学者Nishiyama给出的方案中,捕集系统和下游电推力器直接相连,即面积收缩率为1。基于该方案,Fujita和Tagawa等分别开展了数值模拟和实验研究,但均未对捕集率进行详细分析。在欧空局Romano等给出的方案中,捕集系统和电推力器通过狭窄的通路相连,相当于采用了较小的面积收缩率。基于该方案,Binder等开展了数值模拟和理论分析,结果表明当面积收缩率为1/10时的最优气体捕集效率不到35%,结合霍尔推力器的相关实验研究也未获得净推力。针对面积收缩带来的气体捕集效率不高的问题,Li等提出了一种改进方案,该方案在进气道出口安装了和进气道管径相同的涡轮分子泵,即面积收缩率等于1。由于涡轮分子泵具有较大的正向穿透概率且逆向穿透概率很低,因此能够对分子起到定向引导的效果。基于数值模拟结果,Li等认为通过提升涡轮分子泵转速并优化无量纲管长,捕集率可以达到50%以上。
文献中对气体捕集系统的研究主要集中在方案设计和模拟验证,对自由分子流条件下气体捕集机理的研究相对较少。以往的经典理论大多关注简单的直管透射问题,对于结构更为复杂的气体捕集系统,现有的近似理论模型和数值模拟结果定性上一致但定量上有较大偏差。
为了更好地指导气体捕集系统的优化设计,本文首先对气体捕集系统开展了理论研究,推导得到了捕集率的理论公式,并通过理论公式分析了捕集率的变化规律。然后在理论研究的基础上,针对实际飞行条件,开展了捕集系统的优化设计。
1 捕集机理分析
1.1 物理问题
文献中各种气体捕集系统均可分解为进气道、收缩段以及导流装置三个部分,如图2所示。进气道的几何参数包括入口横截面积、出口横截面积、长度以及入口到出口的过渡型面(如直线型、曲线型、折线型等)。当进气道的几何参数和气固相互作用规律确定后,即可确定来流分子从入口到达出口的概率(正向透射概率,)和反流分子从出口到达入口的概率(反向透射概率,)。导流装置是指能够定向导引分子流动的机械装置,其横截面积记为。分子从正向和反向穿透导流装置的概率定义为和,当导流装置为涡轮分子泵时,和由分子泵的几何参数和转速决定,如果不使用导流装置则二者均为1。进气道和导流装置通过收缩段进行连接,和进气道相比,收缩段的长度通常很短,因此可以近似简化为长度为0的收缩截面并定义面积收缩比为/。
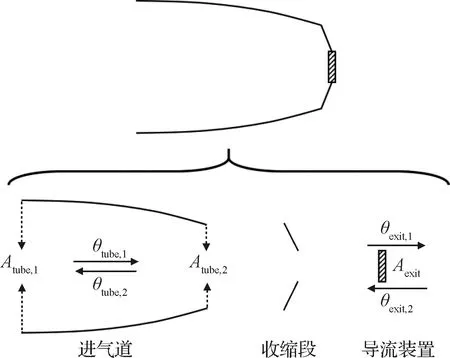
图2 气体捕集系统结构图Fig.2 Composition of an air intake system
在下文的理论分析,需要使用导流装置的净透射率,即分子正向穿透导流装置进入下游且不再返回的概率。除了与和有关,还和下游的密度等条件有关,因此仅依靠捕集系统的参数无法直接确定。但如果≫且导流装置两端的压缩比远小于/,则逆向穿透导流装置的分子可以忽略,此时可以认为近似等于。
1.2 捕集率的平衡模型
Romano等针对进气道为直管的特殊情况(=)给出了捕集率的平衡模型。下面将该模型推广到更为一般的情况(>)。
该模型的基本假设是,在紧贴进气道末端的一段腔体中(如图3(a)的虚框),气体处于完全的平衡态,包括宏观速度为0、热运动速度满足麦克斯韦分布以及空间上均匀分布。

图3 平衡模型示意图Fig.3 Description of the balancing model
将腔体的左侧(进气道)、右侧(导流装置)均简化为具有正向和反向透射率的黑箱,如图3(b),然后对腔体中的气体建立如下的质量守恒方程
=+
(4)
式中:,,分别为
=
(5)
=
(6)
=
(7)
其中,,为分子数密度和通量速度,下标0和ch分别代表来流气体和腔体。对于式(5),由于来流气体的宏观速度(约7.8 km/s)远大于分子热运动速度,可以近似为宏观速度。对于式(6)和式(7),由于腔体气体的宏观速度假设为0,可以通过下式计算
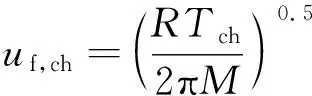
(8)
式中:为普适气体常数,为腔体气体温度,为气体的摩尔分子质量。
将式(5)-(7)代入守恒方程,可以得到腔体气体的压缩比公式

(9)
然后可得捕集率公式
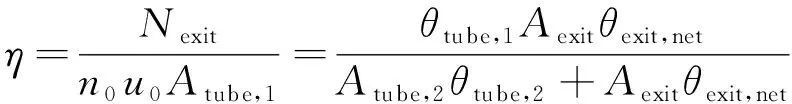
(10)


(11)
Binder等通过平衡模型和数值模拟分别计算了直管构型捕集系统的透射率,二者定性吻合,但平衡模型整体上低估了捕集率。我们认为产生偏差的主要原因是,在平衡态假设下通过式(8)计算的腔体两侧的通量与实际情况不完全相符。具体来说,除了密度存在非均匀分布以外,自由分子流下的速度分布函数也无法达到麦克斯韦分布。在下一节我们通过概率分析给出一种更为准确的透射率模型。
1.3 捕集率的非平衡模型


图4 来流分子进入捕集系统后的可能结果Fig.4 Possibilities of a molecule entered the air intake system
将所有可能的穿透概率相加,即可得到最终的捕集率


…
(12)
简化后为
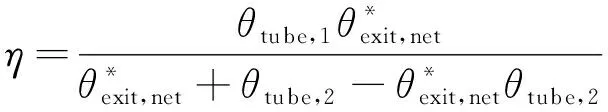
(13)
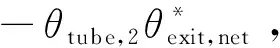
1.4 直管构型捕集系统的捕集率
本节以工程设计中常见的直管构型捕集系统作为分析对象,对上述理论模型进行检验并分析捕集率的变化规律。气固相互作用模型采用与实际飞行数据更为吻合的漫反射模型。
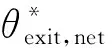
由于直管的左右对称性,正向和反向透射率可以在同一个方向上求解。对于横截面为圆形的直管,Clausing、Hughes等给出了透射率的理论求解方法,在此基础上Cole等获得了透射率的数值解。但对于一般截面形状的直管,特别是工程设计中常用的正多边形截面,则需要通过直接模拟蒙特卡罗(DSMC)或试验粒子蒙特卡罗(TPMC)等分子模拟方法统计获得直管透射率。本文采用TPMC方法计算直管透射率。在蒙特卡罗模拟中,分子发生漫反射后的法向和切向速度需要满足对应的概率分布函数,仿真时可以采用逆变换法或取舍法等方法随机生成,具体过程可参考相关文献。
透射率是无量纲来流速度(简称无量纲速度)和无量纲管长的函数,无量纲速度一般以来流气体的最可几速度(=(2/))作为参考速度,无量纲管长可以以圆管直径作为参考长度。Li等的数值模拟结果表明以(为横截面积)做参考长度时,正多边形管和圆管的透射率几乎相同,因此本文采用作为参考长度计算无量纲管长。本文中,无量纲速度和无量纲管长分别记为和。另外,对于从出口回弹至进气道的分子,一般认为其仅具有热运动速度而不具有特定的宏观速度,因此反向透射率对应的无量纲速度是0。
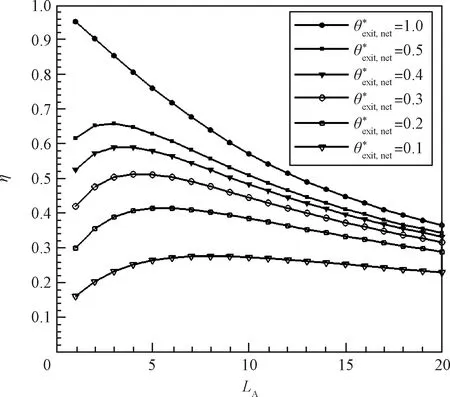
图5为=0和=10.15时透射率与无量纲管长的关系。当增加时分子穿透直管的难度增加,当减小时来流气体的准直性减弱,因此增加或减小均会导致下降。由图可知,直管截面形状是圆形或方形对透射率没有明显影响,证明了作为无量纲管长的合理性。本文和文献[3]的模拟结果吻合很好,验证了本文模拟程序的可靠性。

图5 透射率与无量纲管长的关系Fig.5 Transmission probabilities of different LA
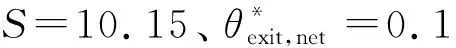

图6 理论模型和数值模拟的捕集率对比Fig.6 Transmission probabilities calculated by theoretical models and numerical simulation

图取不同值时透射率和无量纲管长的关系Fig.7 Influence of on transmission probabilities
2 捕集系统设计
2.1 设计方法

真实的大气环境可能包括多种组分,在相同来流速度下每种组分的无量纲速度并不相同,因此各组分的最优无量纲管长也不相等。实际设计中可以先计算出各组分捕集率随的变化规律,然后根据各组分的分子量和摩尔分数确定来流气体的质量捕集率随的变化规律并确定最优的。
实际飞行中还需要考虑进气道侧壁面给卫星带来的额外阻力。实际设计中可以采用多孔准直器缩短进气道长度(如图8),即将单个直管替换为相同无量纲管长下的一簇直管。但准直器内部隔板额外占用的入口面积会降低捕集率,因此需要合理地确定准直器的分割层数,以获得最佳的推进性能。
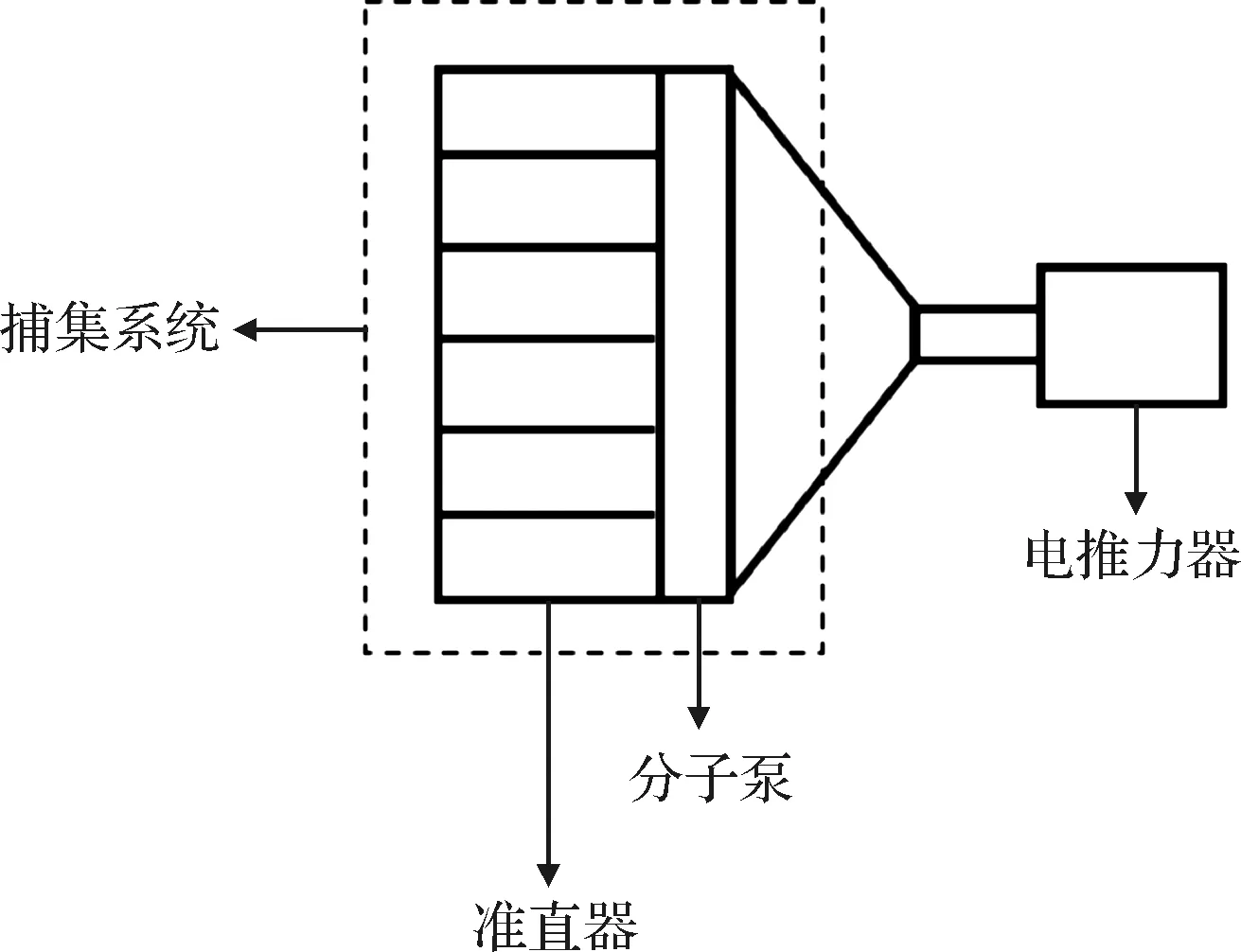
图8 捕集系统示意图Fig.8 Scheme of the air intake system
基于上述讨论,捕集系统的优化设计步骤为:
1)选定实际飞行轨道,根据大气模型确定来流条件;
2)选择合适的涡轮分子泵,通过体积抽速换算出来流气体各组分对应的分子泵正透射率;
3)通过非平衡模型计算各组分捕集率,再结合各组分的分子量和摩尔分数确定来流气体的质量捕集率,最后确定最优的无量纲管长;
4)保证无量纲管长不变的前提下,以最大推阻比为目标,确定合适的准直器分割层数。
2.2 参数优化
本节选择150 km的近地轨道为实际飞行轨道,根据2.1节的优化设计步骤,开展捕集系统的参数优化。
第一步,确定150 km高度下的来流条件。由NMLMSISE-00模型给出的中等太阳活动强度下(F10.7=140)的大气温度为691 K,O,N和O的摩尔分数分别为37.5%、58.6%、3.9%。设来流速度为7800 m/s,则O,N,O的无量纲速度分别为9.23、12.21、13.05。
第二步,确定涡轮分子泵的正向透射率。已知分子泵的体积抽速和之间满足如下关系
=
(14)
式中:为分子泵的入口面积,为通量速度。本文选择了PFEIFFER公司生产的ATH3200M型涡轮分子泵,表1为产品说明书中给出的N,He,H,Ar四种气体的体积抽速。为了得到该分子泵对空气各组分的正向透射率,首先建立透射率与气体分子量之间的关系。图9为换算得到的和分子量的关系。从图中可以看出,与ln存在近似线性关系。然后通过线性插值,得到O,N和O的正透射率分别为23.7%、29.2%和30.8%。该型产品在涡轮分子泵之后还有一个牵引分子泵,使得它具有10以上的压缩比,远大于吸气式电推进1000~10000倍压缩比的需求,因此可以忽略下游回流对透射率的影响。此外,该型分子泵的直径为320 mm,因此将进气道直径也设为320 mm。
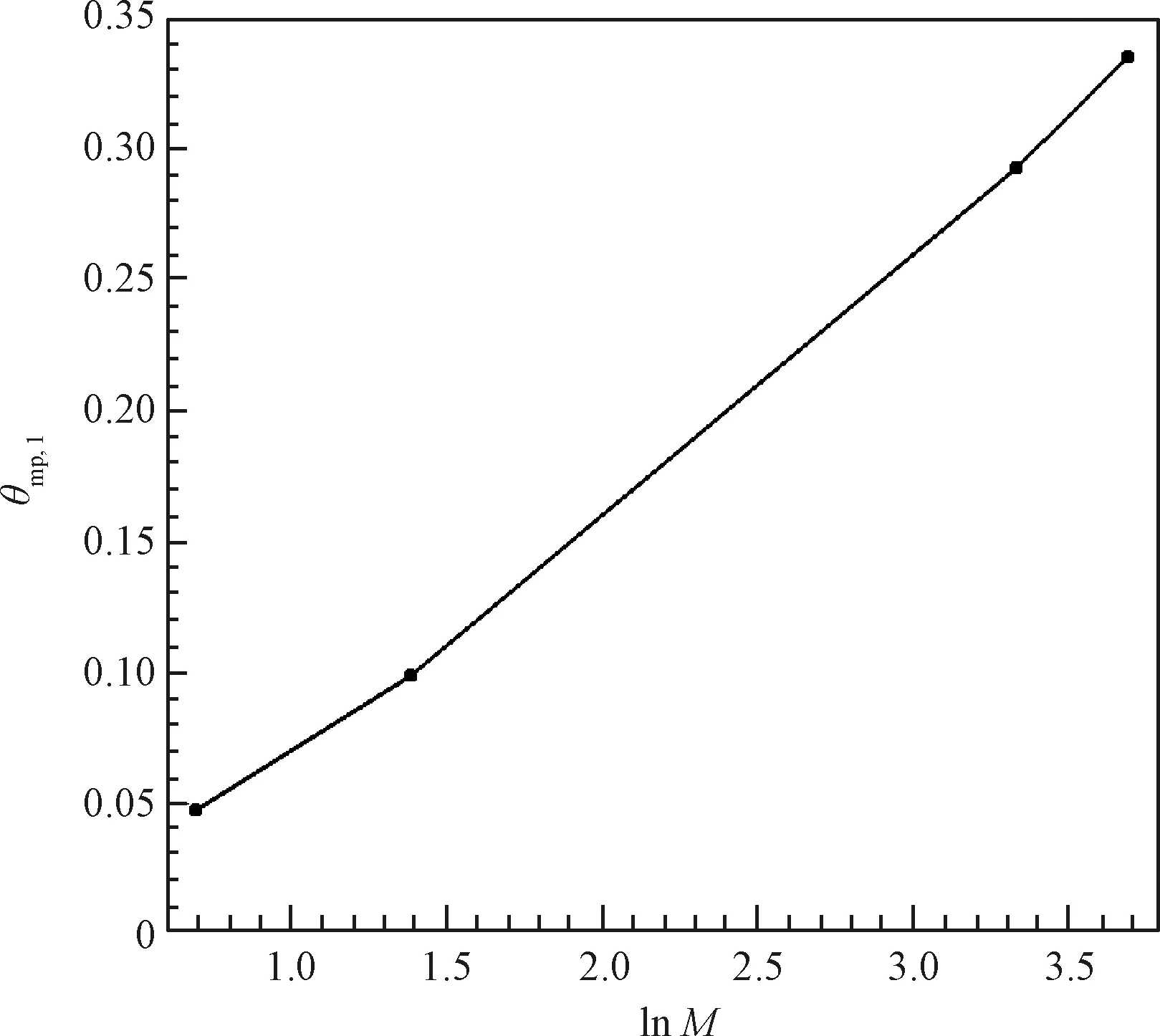
图9 分子泵正透射率和分子量的关系Fig.9 The forward transmission probabilities of molecular pump for different molecular weights

表1 ATH3200M分子泵的体积抽速Table 1 Pumping speed of ATH3200M
第三步,对无量纲管长进行优化。首先,对于各组分,分别通过TPMC模拟得到相应无量纲来流速度下的直管透射率,再结合涡轮分子泵正向透射率,通过非平衡模型计算出捕集率,结果如图10所示。可以看出,O的透射率最大、N次之、O最小,即分子量越小捕集率越低。根据各组分的分子量和摩尔浓度,最终得到空气的质量捕集率,结果表明最大捕集率为50.8%,对应的无量纲管长为4.28。
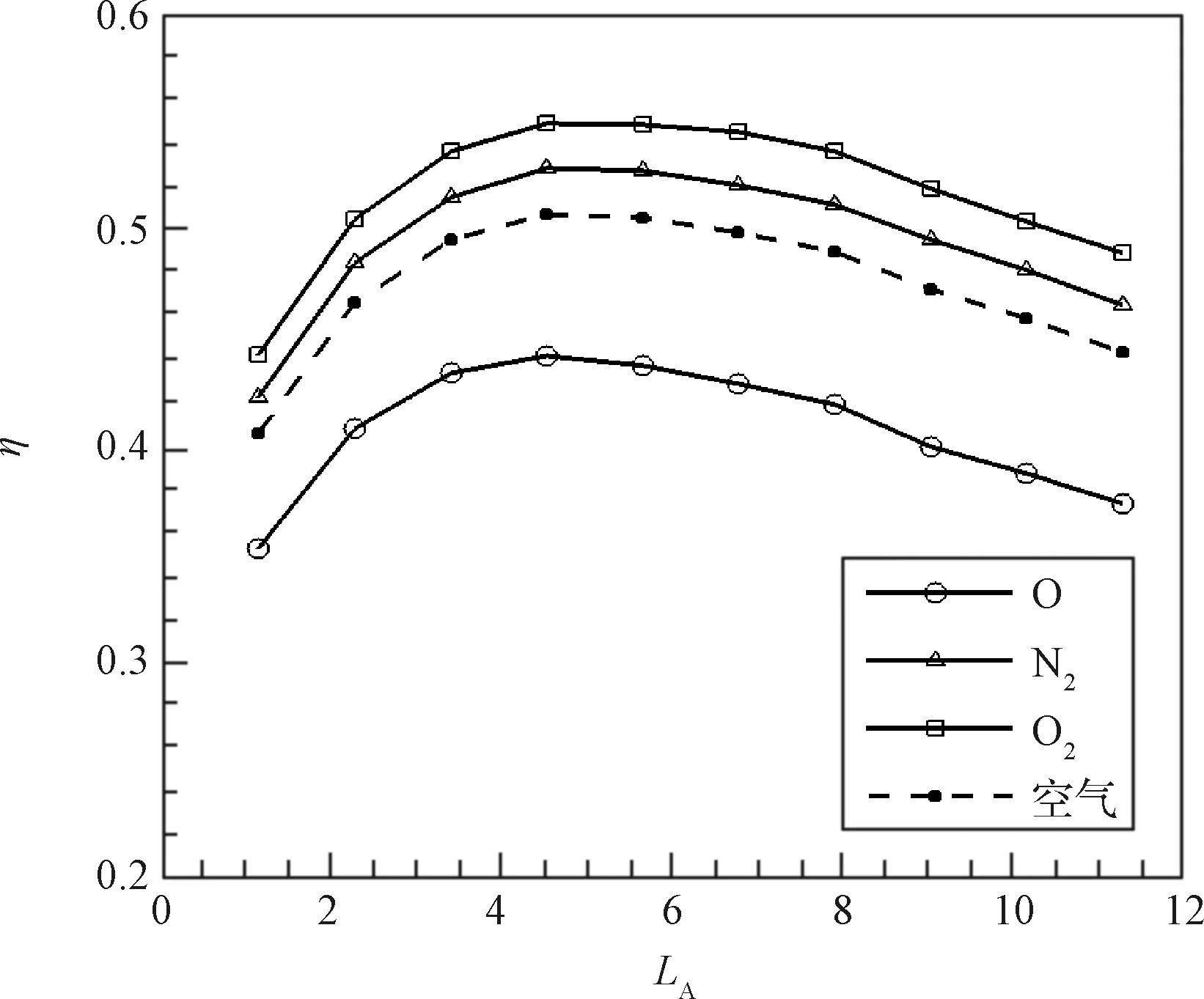
图10 捕集率和无量纲管长的关系(150 km高度)Fig.10 Collection efficiencies of different LA at 150 km

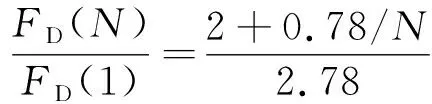
(15)

(16)
式中:为准直器内部隔板厚度。因此,推阻比()可以写为

(17)
图11为Δ=1 mm的计算结果,可以看出,=4时推阻比可以获得最大提升(提升幅度为17.2%),对应的准直器长度变为0.343 m。由于圆形截面分割更为复杂,因此实际分割层数不一定为4,但可以将0.343 m作为设计准直器的参考长度。

图11 推阻比和准直器分割层数的关系Fig.11 Thrust-drag-ratio of different dividing layers
2.3 讨 论
本节进一步对当前方案中的一些不足和改进方向进行讨论。
目前方案中假设所有分子沿正向穿透分子泵的概率均为,但这种假设会一定程度上高估气体捕集率。原因是来流分子穿越进气道的过程中一部分未与侧壁面发生碰撞(称为直接透射分子),另一部分至少与侧壁面发生一次碰撞(称为间接透射分子),而直接透射分子由于保留了来流的宏观速度,因此其正向穿透涡轮分子泵的概率会因为无量纲转速的降低而显著下降。图12为TPMC模拟得到的=10.15时来流分子以直接和间接的方式穿透直管进气道的概率(称为直接透射率和间接透射率,二者之和为)。可以看出,当<10时>20%,因此需要对直接透射分子的影响予以重视。一方面可以通过分子模拟对分子泵进行精细建模以获取更为准确的捕集率,另一方面应考虑优化分子泵参数以提升直接透射分子的透射率。
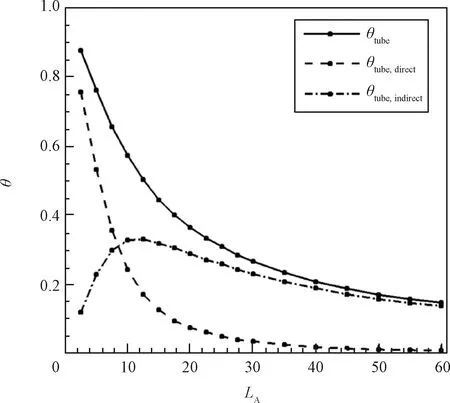
图12 直接透射率θtube,direct、间接透射率θtube,indirect和无量纲管长的关系Fig.12 Direct and indirect transmission probabilities of different LA
目前的理论分析和方案设计主要是基于完全漫反射模型,但实际情况中分子与壁面首次发生碰撞时,入射速度很大且入射角很小,其散射规律可能和完全漫反射模型有较大差异。可以考虑使用更贴近实际的CLL模型或者分子动力学(MD)的模拟数据来研究气固相互作用规律对捕集率的影响。
3 结 论
本文对吸气式电推进的气体捕集系统开展了理论分析和设计优化。通过对文献中系统的简化抽象,分析获得了影响捕集率的关键参数,在此基础上给出了准确的捕集率理论模型(非平衡模型)。采用捕集率的非平衡模型,分析了直管构型捕集系统的捕集率变化规律,结果表明:对于给定的出口净透射率,存在使捕集率达到最大值的最优无量纲管长,且最优无量纲管长随出口净透射率降低而减小。
利用理论模型,以150 km的绕地轨道为例,对捕集系统开展了设计和优化。基础方案采用直管构型加等管径涡轮分子泵的组合。通过参数优化,确定了系统的无量纲管长(4.28)以及最大捕集率(50.8%),并以最大推阻比为优化目标确定了准直器的长度参考值0.343 m。
后续研究中需要对涡轮分子泵透射率和气固相互作用规律开展更精细的研究,以获得更为准确的捕集率影响规律。

