新能源示范城市建设对城市土地利用效率的影响及其空间溢出效应

王梦成，卢新海，，马宇翔，匡 兵，唐一峰

（1.华中科技大学公共管理学院，湖北 武汉 430074；2.华中师范大学公共管理学院，湖北 武汉 430079）

1 引言

城市土地利用效率（Urban Land Use Efficiency,ULUE）是城市系统与土地利用系统间耦合水平的直接体现，也是高质量发展背景下衡量生产要素合理配置、高效利用的关键指标[1]。在工业化快速发展阶段，中国城市经济发展过度依赖传统化石能源，城市环境污染严重，ULUE较为低下。为解决城市经济高质量发展和土地低效率利用的矛盾困境，2014年国家能源局确定建设81个新能源示范城市和产业园区。新能源示范城市建设（以下简称“示范城市建设”）通过促进城市系统的物质循环和能量流动[2]最终影响到土地利用系统的ULUE。因此，探索新能源示范城市建设对ULUE的影响不仅有助于科学评价新能源示范城市建设的政策效应，也为有效提高ULUE提供了新的思路。

土地利用效率的概念最早来源于农业土地利用效率，随着城市化的发展，学者们开始关注ULUE[3]。目前，学界主要围绕ULUE指标体系构建[4]、测算方法[5-6]等对不同尺度下ULUE的时空特征[7]、区域差异[8]及其收敛性[1]等方面展开了系统研究。同时，ULUE的增长也受到区域一体化水平[9]、交通基础设施[10]、土地市场化水平[11-12]、产业结构[13]等多种因素的影响。在新发展阶段，为调控城市经济的可持续发展，中国政府先后提出低碳城市[14-16]、智慧城市[17]、创新型城市[18]等一系列试点政策，对区域土地利用系统产生了较大影响。那么，同样作为国家重大战略安排的新能源示范城市建设试点政策对ULUE提升是否具有类似的作用机制和政策效应？较多学者对新能源示范城市建设的发展前景与动力[19-20]、影响因素[21-22]及试点政策效应评价[23-26]等方面进行了深入的探讨。与本文密切相关的文献主要体现在政策效应的评价上，学者们以示范城市建设为政策冲击，探讨其对能源使用结构[23]、产业结构[24]、区域经济发展[26]以及污染治理[25]的影响效应，为本文探讨新能源示范城市建设对ULUE的影响提供了理论依据。

同时，随着区域经济一体化进程的加快，区域间合作与竞争日益频繁，本地区土地开发利用在空间上会产生一定的外部性，从而对相邻区域ULUE产生显著影响[27-28]。LESAGE[29]将这种“外部性”引入空间计量经济学中并将其定义为“空间溢出效应”。已有研究表明，经济发展水平[28]、交通基础设施[10]、财政支出[27]等因素对ULUE增长具有显著的空间溢出效应，而在空间效应角度探究政策变迁与制度安排对ULUE影响的相关文献相对较少。如果忽略了试点政策的空间溢出效应，容易导致评估结果产生偏误从而低估试点政策的政策效应[30]。基于此，本文以中国2014年设立新能源示范城市作为准自然实验，通过构建PSMDID和空间计量模型，探究新能源示范城市建设对ULUE的影响及其空间溢出效应，以期为科学评估新能源示范城市建设对ULUE增长的净效应提供参考。

2 理论分析

新能源示范城市建设作为实现中国经济高质量发展的一项重要政策安排，受到中央和地方的“双重关照”[31]。城市土地是新能源示范城市建设的“直接承载者”与“主要参与者”，示范城市建设通过畅通人流、物流、信息流等流通渠道，影响到城市土地利用变化状况，进而影响ULUE。通过梳理已有研究[25-26]发现，新能源示范城市建设通常以结构效应、集聚效应和技术效应等路径影响ULUE（图1）。

图1 新能源示范城市建设对ULUE的影响机制Fig.1 Impact mechanism of new energy demonstration city construction on ULUE

一是结构效应。主要包括土地结构和产业结构两个方面的内容：一方面，示范城市建设通过促进人力、资本、技术等生产要素跨区域流动，强化了区域间的空间联系。不同区域的生产格局会通过扩散边际效应[4]加剧不同区域之间的竞争，而市场竞争使得产业结构不断升级，土地利用进入结构性调整阶段。结构决定功能，地方政府会根据不同区位土地的资源禀赋与竞争优势，实施差异化、精细化的土地管控政策和产业发展政策，进一步促进土地利用效率提升。另一方面，示范城市建设的推进过程会使高新技术产业在市场选择下脱颖而出，产业结构的高级化有利于土地利用结构的不断优化和城市土地的高效利用。同时，示范城市建设能够畅通要素流通渠道，降低企业的生产和贸易成本，在这一过程中优质生产要素不断流向新能源相关高新产业，传统弱竞争力产业被逐渐置换，产业机构合理化趋势更加明显，最终影响城市土地的集约利用状况。

二是集聚效应。主要包括土地要素集聚和非土地要素集聚两个方面的内容：一方面，随着新能源产业的不断发展，产业的规模化、专业化和合作化生产的需求要求城市土地要素不断集聚以提高土地资源承载量和市场潜力，从而发挥城市土地利用的规模效应[4]。另一方面，由于土地的资源稀缺性和位置固定性，土地要素的空间集聚使得城市土地所承载的产业也高度集聚，进一步提升了土地的区位优势，从而吸引更多的人力、资本、技术等非土地要素向具有比较优势的集聚空间集中，在这一过程中，示范城市建设投入资本通过结构效应产生较为广泛的产业关联效应和投资乘数效应，扩大了对城市土地产出效益的带动作用[32]，进一步刺激城市土地向投资回报高的产业进行分配和重组。此外，不同城市的非土地要素集聚格局会产生经济生产效率的空间溢出，反过来促进城市土地利用结构的重组，形成效率循环递增的能级传递机制[2]。

三是技术效应。主要体现在创新技术人才和创新技术水平两个方面：一方面，示范城市建设通过吸引高技能人才集聚，能够加速人力资本的积累，形成高技能人才“蓄水池”，减少了企业的人才搜索和培训成本[33]，为企业进行技术创新提供了良好动力。另一方面，创新技术人才流动产生知识溢出，通过技术关联效应带动相邻区域创新技术水平的提升。示范城市建设对产业发展的促进作用能够对相邻区域形成良好的示范效应，有利于相邻区域通过模仿学习提升自身创新技术水平。并且，示范城市建设改善了城市技术创新环境，创新要素能够进行充分碰撞交流，有利于提高创新技术效率。创新技术人才和创新技术水平两方面因素的相互叠加在一定程度上影响区域土地的投入—产出效率。WANG等[24]的研究为示范城市建设的技术效应提供了实证证据。

3 研究方法与数据说明

3.1 PSM-DID模型

倾向得分匹配（Propensity Score Matching, PSM）能够在满足DID的共同趋势假设的同时消除样本选择偏差，双重差分（Difference-In-Difference, DID）能够很好地解决城市经济发展过程中由发展惯性或其他因素引起的“时间效应”并得出政策处理效应[34]。本文以新能源示范城市建设作为一项准自然实验，通过构建PSM-DID模型，将2014年设立的示范城市定义为实验组，非示范城市定义为控制组，实证检验新能源示范城市建设对ULUE的影响效应。首先，本文通过logit模型计算出样本城市获批新能源示范城市的概率，按照一对一、有放回的“K阶近邻匹配”找到各项特征与实验组最接近的控制组进行倾向得分匹配；其次，利用匹配后的实验组和控制组进行DID回归分析。本文设定政策冲击变量Treated、政策时间虚拟变量Period以及两者的交互项DID = Treated×Period。PSM-DID模型设定如下：

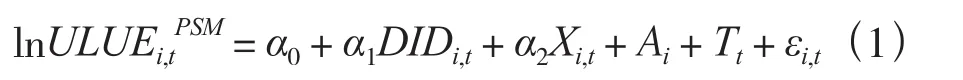
式（1）中：i表示城市；t表示年份；ULUEi,tPSM为被解释变量，表示城市土地利用效率，结合已有研究[3]，本文被解释变量选取了二三产业产值增加值与城市建设用地面积的比值来予以衡量；DIDi.t为核心解释变量，即政策冲击变量Treated与政策时间虚拟变量Period的交互项（DID = Treated×Period），如果某一城市为新能源示范城市，则Treated=1，否则Treated=0，考虑到政策文件发布时间在2014年上半年，故将2014年作为政策冲击年份，即2014年之后的年份Period=1，2014年之前的年份Period=0；α1为核心解释变量的系数，表示新能源示范城市建设对ULUE的净影响；Xi.t为一系列控制变量。同时，本文采用双向固定效应的方法，即控制了城市个体效应Ai和年份效应Tt，εi.t为随机扰动项。

本文选取以下指标作为控制变量：人力资本水平（EDU）[31],以普通高等学校在校学生数与年末总人口的比重来衡量；研发投入水平（R&D）[25]，以科学支出占地方财政一般预算内支出的比重来衡量；政府干预水平（GOV）[26]，以地方财政一般预算内支出占地区生产总值的比重来衡量；产业结构高级化（ISA）[35]，用产业结构层次系数来表征产业结构高级化程度，计算公式如下：

式（2）中：ISA表示产业结构高级化指数，ISA值越大，表示该城市产业结构高级化程度越高；m为三次产业的权重，第一、二、三产业依次赋值为1、2、3；Yi,m,t表示i城市在t年第m产业占该地区总产值的比重。

3.2 空间计量模型

从空间计量角度来看，新能源示范城市的建立不仅对本地区的土地利用产生影响，对邻近地区ULUE也可能产生影响。如果忽略新能源示范城市建设的空间溢出效应，可能会低估其政策效应[30]。鉴于此，本文构建空间计量模型来刻画新能源示范城市建设的空间效应，一般包括空间滞后模型、空间误差模型和空间杜宾模型。根据ELHORST[36]与LESAGE等[29]的研究，本文以DID作为主要解释变量，构建如下空间计量模型：

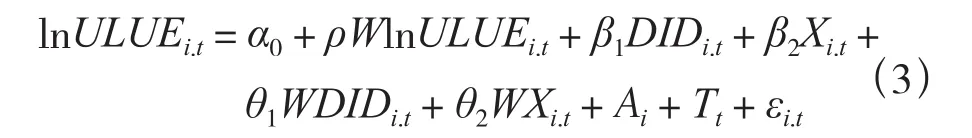
式（3）中：W为二进制邻接空间权重矩阵；WlnULUEi.t和WXi.t分别表示被解释变量和解释变量的空间依赖；ρ和θ分别为WlnULUEi.t和WXi.t的回归系数；β为Xi.t的回归系数；ρWlnULUEi.t为被解释变量的空间滞后项，表示邻近区域的被解释变量对本区域被解释变量的影响；θ2WXi.t为邻近区域平均观测值的空间滞后变量，表示邻近区域的解释变量对被解释变量的影响，其他变量含义同式（1）。此时，式（2）表示空间杜宾模型。当ρ = 0时，式（2）表示空间误差模型；当θ + ρβ = 0时，式（2）表示为空间滞后模型。

由于在空间计量模型中引入了空间滞后项，所以在进一步解释空间计量模型的回归参数时需要考虑解释变量的边际影响。LESAGE等[29]指出自变量矩阵WXi.t的系数θ并不能完全衡量解释变量对被解释变量的影响，需要将空间模型的总效应分解为直接效应和空间溢出效应，其表达式为：

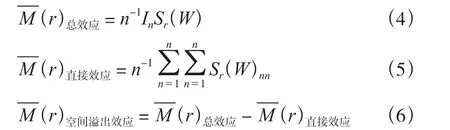
3.3 数据说明

基于数据的完整性和可得性，本文共选取2003—2019年中国285个地级及以上城市的面板数据。本文使用地级市层面的数据样本，为确保研究结论的稳健性，本文从2014年中国新能源示范城市名单中剔除了县级市、区（自治州）和产业园区的样本，进而生成本文的实验组，共56个，控制组城市共229个。新能源示范城市空间分布如图2所示。

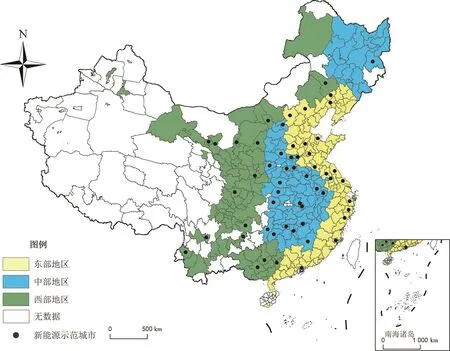
图2 新能源示范城市空间分布Fig.2 Spatial distribution of new energy demonstration cities

本文所用指标数据均来源于《中国统计年鉴》（2004—2020年）、《中国城市统计年鉴》（2004—2020年）、各地级市的统计年鉴（2004—2020年）及其社会经济发展统计公报。缺失值统一采用插值法补齐。同时为了减少价格因素的影响，本文以2003年为基期对所有价格均进行了平减调整。表1为各个变量的描述性统计结果。

表1 主要变量描述性统计Tab.1 Descriptive statistics

4 实证结果与讨论

4.1 基准回归结果

本文利用Stata 15.2软件，通过PSM为每一个新能源示范城市寻求条件相类似的控制组样本，图3为匹配前后的倾向得分核密度分布图，可以发现匹配前控制组分布较为分散，与实验组的倾向得分值存在显著差异，经过匹配后，两组之间的差异显著缩小，甚至匹配后出现了样本覆盖的情况，说明匹配后实验组和控制组各方面特征较为接近，匹配效果较好，下文使用PSM-DID进行估计较为合理。

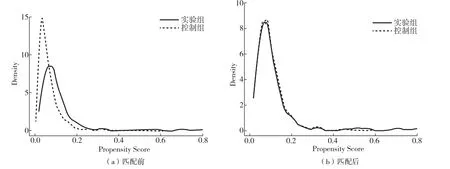
图3 匹配前后的倾向得分核密度分布图Fig.3 The kernel density distribution of propensity scores before and after matching

本文利用Stata 15.2软件检验新能源示范城市建设的净效应，并在基准回归的基础上依次加入控制变量，所有回归均采用了以地区为聚类变量的聚类稳健标准误。回归结果见表2所示，模型（1）是没有加入控制变量时的估计结果，模型（2）—模型（5）是加入控制变量的结果。可以发现，核心解释变量的回归系数均显著为正，这表明新能源示范城市建设对地区ULUE有着显著的促进作用。

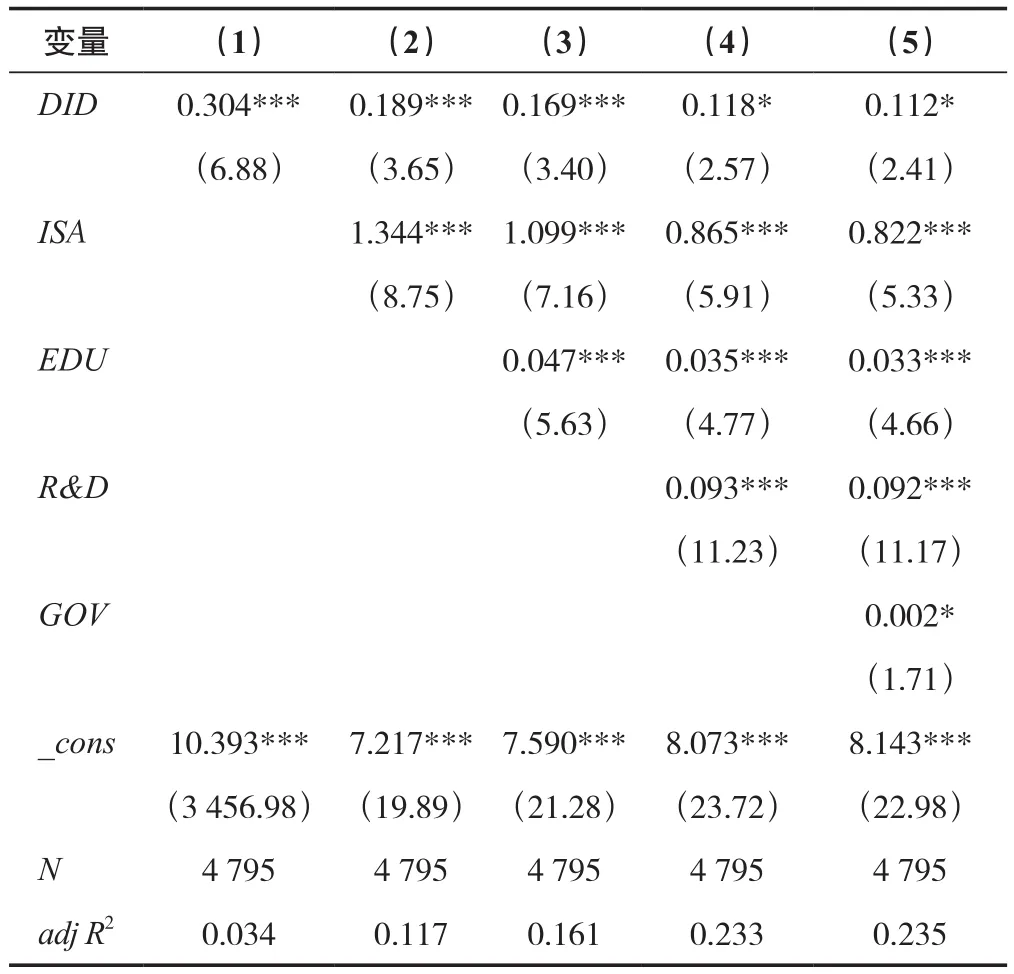
表2 PSM-DID基准回归结果Tab.2 Results of benchmark regression of PSM-DID

4.2 空间溢出效应分析

为进一步分析新能源示范城市建设的对邻近地区ULUE的空间溢出效应，需要使用空间计量模型对示范城市建设的影响效应进行分解。在使用空间计量模型之前，需要对被解释变量进行空间自相关检验。本文采用常用的Moran’sI对城市土地利用效率（lnULUE）进行空间自相关检验，权重矩阵采用二进制邻接空间权重矩阵。计算结果（限于文章篇幅，本文并未报告，备索）显示，Moran’sI均大于零，且在1%的显著性水平上通过检验，表明中国城市土地利用效率的空间溢出性较强，且呈现空间正相关性[10]。因此，本文可以采用空间计量模型考察示范城市建设对ULUE的影响。

根据前文所构建的空间杜宾模型，采用Matlab R 2017b软件以最大似然估计方法估计了2003—2019年中国新能源示范城市建设对ULUE的影响，估计结果如表3模型（4）所示。为了对比，表3（1）—（4）列还给出了OLS模型、空间滞后模型、空间误差模型和空间杜宾模型的估计结果。由表3可知，核心解释变量DID仅在OLS模型与空间滞后模型中分别通过了1%和5%的显著性检验，并且根据以下4个模型的调整R2值和自然对数似然函数值（logL）的大小，以及解释变量估计系数的经济学含义，同时结合Hausman检验结果，选择时空固定效应下的空间滞后模型进行实证检验更为合理。故下文主要针对时空固定效应的空间滞后模型结果进行分析。

表3 新能源示范城市建设与ULUE的实证检验结果Tab.3 Empirical test results of new energy demonstration cities on ULUE

当存在空间溢出效应时，前文的估计系数仅仅在作用方向和显著性上是有效的，不能直接反映解释变量对被解释变量的边际效应[37]。因此，根据ELHORST[36]与LESAGE等[29]的理论，本文进一步将各因素对ULUE的影响分解为直接效应和空间溢出效应，结果如表4所示，核心解释变量新能源示范城市建设（DID）对本市ULUE的直接效应为正且通过了1%的显著性检验，表明示范城市建设对本地区ULUE提升具有促进作用。这与徐换歌等[26]得出的结论一致。示范城市建设使得城市土地等生产要素在空间配置上进一步趋于合理化，促进城市土地等要素向具有比较优势的产业流动，产业合理化趋势愈加明显，最终影响到城市土地的集约利用状况，从而提升ULUE。同时，示范城市建设的空间溢出效应为正且通过了1%的显著性检验，这表明示范城市建设不仅提高了本地区的ULUE，同时也有利于邻近地区ULUE的提升，可能的原因是示范城市建设通过发挥技术效应和结构效应，促进了区域间优质要素的相互流动，以知识溢出和技术扩散等形式，对邻近地区形成了具有良好的示范效应和空间辐射效应，加强了邻近地区的“看齐意识”，邻近地区通过模仿和学习提升自身的创新技术水平，促进区域ULUE的共同提升。

表4 各因素对ULUE的空间效应分解结果Tab.4 The decomposition results of the spatial effects of various factors on ULUE

其他控制变量中，产业结构高级化（ISA）、人力资本（EDU）、研发投入（R&D）的直接效应和空间溢出效应均通过了1%的显著性检验，而政府干预（GOV）并不显著。产业结构从第一产业向第二、三产业的顺向演进体现了示范城市建设的结构效应，通过畅通各类优质生产要素在产业间和区域间的快速流动渠道，要素产业间的配置效率大大提高，促进了本地和邻近地区ULUE的提升，表现为区域协同发展态势。人力资本和研发投入基于地理空间的集聚同样能够产生集聚效应，使新能源城市建设投资能够充分发挥投资乘数效应和规模效应，进而拉动本地区ULUE的提升，而知识外溢和创新扩散的存在推动了区域技术进步和经济发展[38]，对邻近地区ULUE存在正向空间溢出效应。

4.3 区域异质性分析

中国幅员辽阔，区域之间发展不均衡，东部地区、中部地区和西部地区的ULUE存在较大差距，因此分析示范城市建设对ULUE的空间效应有必要考察地理区位的差异性。本文通过构建东、中、西部地区虚拟变量进行了异质性回归分析，表5分别给出了基于空间滞后模型的估计结果。

表5结果显示，核心解释变量新能源示范城市建设（DID）在模型（1）—模型（3）中均为正，这表明示范城市建设对东、中、西部地区的ULUE提升均具有促进作用，这也再次检验了基准模型的稳健性。但值得注意的是，模型（1）中的回归系数并不显著，而模型（2）和模型（3）均通过了1%的显著性检验，且回归系数远大于模型（1），这表明示范城市建设对中西部地区的ULUE提升存在更大的促进作用，而对于东部地区经济相对发达城市的促进作用并不明显，总体上呈现出“边际效应递减”的规律。这一结论与刘瑞明等[39]的研究结论相一致。本文对此的解释是东部经济发达地区在新能源开发利用技术、城市土地集约利用、环境保护意识等方面本身就相对完善，同样的示范城市建设政策对于这些地区的作用更多的是“锦上添花”；而对于中西部地区经济发展较为落后的城市，示范城市建设所带来的政策优惠和财税补贴则能起到“雪中送炭”的作用，对ULUE提升所产生的边际效应更大。

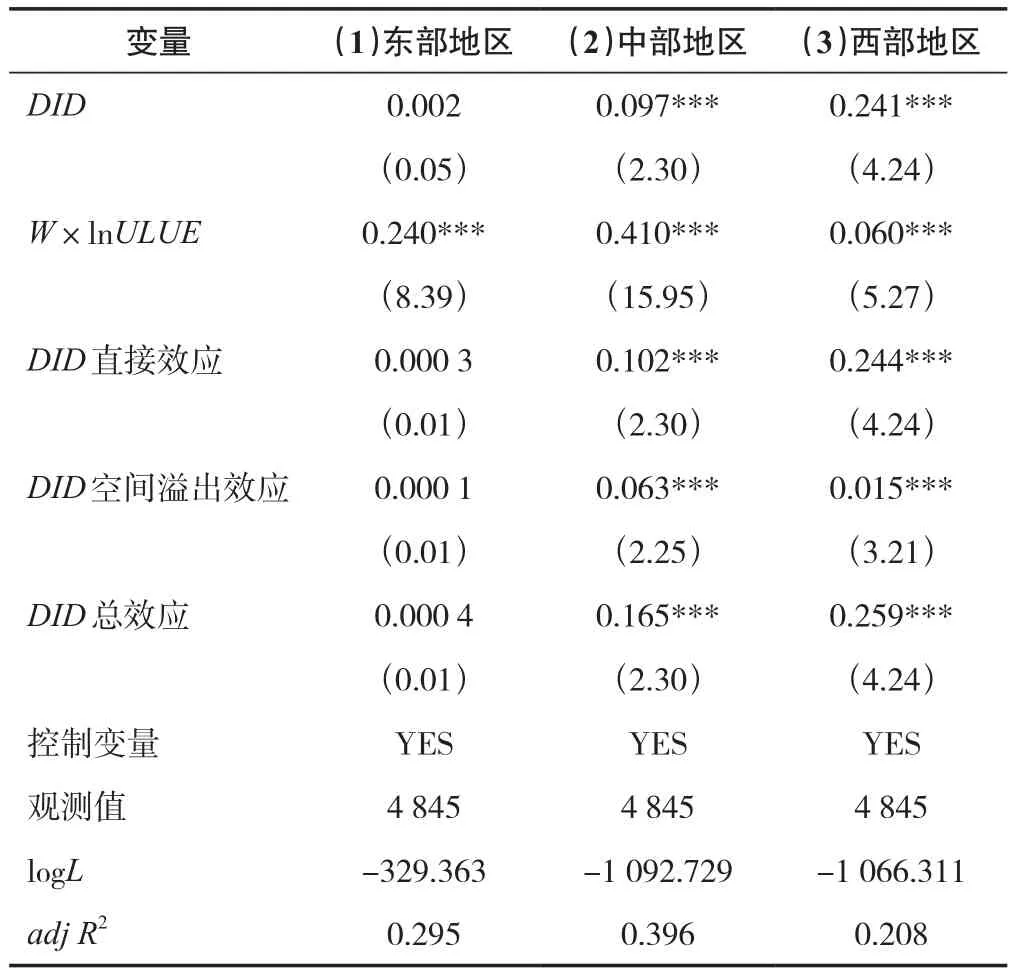
表5 区域异质性回归结果及空间效应分解Tab.5 Regression results of regional heterogeneity and decomposition of spatial effects

进一步对比中西部地区示范城市建设的空间溢出效应，可以发现，在西部地区，示范城市建设对ULUE的提升更多表现为直接效应，空间溢出效应只占总效应的5.9%，而在中部地区，空间溢出效应所占比例提升至38.4%。可能的原因是东部地区由于其本身经济发展基础较好，示范城市建设所带来的边际效应较小，并不会产生较为明显的直接效应和空间溢出效应；而西部地区社会经济发展相对滞后，示范城市建设能够对本地区城市土地等资源的优化配置产生较为明显的促进作用，从而提升ULUE，表现为直接效应占统治地位而空间溢出效应占比较低；中部地区社会经济发展处于东部和西部地区之间，较之西部地区，中部城市之间具有相对流畅的要素流通渠道，从而在空间上更易形成区域联动、相互协同的发展态势。

4.4 稳健性再检验

为了确保回归模型结果的稳健性，本文在PSM—DID的基础上再次进行了两项稳健性检验。第一，替换被解释变量。借鉴已有做法[40]，采用以产出导向的规模报酬不变的超效率SBM模型测算得出的城市土地利用效率（ULUESBM），回归结果如表6模型（1）所示。第二，改变样本范围。考虑到政府在规划新能源示范城市时，会侧重于发挥行政级别较高的直辖市、省会城市及副省级城市的风向标作用，由此导致处理组与控制组受政策冲击存在异质性[35]，本文对285个样本城市中的直辖市、省会城市及副省级城市共33个城市进行了剔除，回归结果如表6模型（2）所示。在替换被解释变量和剔除重点城市后，示范城市建设依然显著影响ULUE，且直接效应、空间溢出效应和总效应均通过显著性检验，再一次证实了前述结论具有稳健性。

表6 稳健性检验结果Tab.6 Results of robustness tests

5 结论与政策建议

5.1 结论

本文以中国新能源示范城市建设试点政策作为一项准自然实验，利用2003—2019年中国285个地级及以上城市的面板数据构建了PSM-DID模型和空间计量模型，实证检验了新能源示范城市建设对ULUE的影响，得到如下结论：（1）新能源示范城市建设显著影响着ULUE。新能源示范城市建设通过结构效应、集聚效应及技术效应等路径转换区域间生产要素流动方向与频率，影响着城市土地利用方式与程度。基准回归分析表明，相较于非试点城市，示范城市建设使ULUE提高11.2%。意味着新能源示范城市建设有利于ULUE的提升。（2）新能源示范城市建设不仅有利于本地区ULUE提升，而且对邻近地区的ULUE同样具有促进作用。空间溢出效应分析表明，示范城市建设具有显著的空间溢出效应，且空间溢出效应占总效应的40.4%。（3）新能源示范城市建设对ULUE的空间溢出效应在城市地理区位上存在显著差异。异质性分析表明，示范城市建设对ULUE的空间溢出效应呈现出从东部到中部再到西部城市依次增强的趋势，且相较于东部地区城市，中西部地区能够通过示范城市建立获得ULUE的显著提高。

5.2 政策建议

（1）促进新能源示范城市建设的有序扩散，提高政策供给质量。中央政府应进一步扩大新能源示范城市的试点范围，持续完善新能源示范城市遴选标准，构建覆盖内容更加科学的评选体系，有序增加示范城市数量。同时，应充分考虑到城市的区位异质性，为不同区域的新能源示范城市建设提供“量身定做”的标准和优惠政策，支持地方新能源城市建设“百花齐放”。（2）发挥新能源示范城市建设的结构效应与技术效应，激发城市土地活力。地方政府应利用示范城市建设对ULUE增长的助推作用，帮助中西部经济发展较为落后的城市进行“产学研”一体化建设，强化新能源科技成果转化，盘活中西部地区闲置土地，在高质量发展阶段实现“迎头赶上”和“弯道超车”。（3）把握新能源示范城市建设的正向空间溢出效应，积极进行跨区域合作与发展。应进一步发挥新能源示范城市建设的空间溢出效应，加强城市群的联动发展，助力区域ULUE的稳步提升。