基于融合相似原理的天然气压缩机性能曲线研究

刘贺宇 刘金虎 张凯灵 肖大伟 徐亚男 梁昌晶

（1.中国石油集团渤海石油装备制造有限公司钻采装备销售公司；2.中油龙慧自动化工程有限公司；3.中国石油西南油气田公司输气管理处；4.国家管网集团西部管道有限责任公司塔里木输油气分公司；5.国家管网集团北方管道有限责任公司廊坊输油气分公司）

离心式压缩机被广泛用于天然气长输管道工艺。其在出厂和投产使用前需进行性能试验，在进气状态和转速确定的条件下，测试各种参数随进气量变化的曲线，用于确定最优运行状态，指导现场人员操作[1-2]。但由于进口条件（主要为入口压力和入口温度）和试验气体性质的不同，厂家提供的性能曲线与实际工况下的性能曲线差异较大[3]。压缩机性能曲线的正确与否直接关系到压缩机的能耗水平，因此需将试验工况下的性能曲线换算为实际工况下的性能曲线。在此，全面分析两种近似相似原理的不同，指出引起性能参数计算结果误差的原因，提出基于融合相似原理的性能曲线预测方法，提高性能换算精度，以期更好地指导压缩机的运行和维护，降低压缩机能耗。

1 相似原理

对于离心式压缩机，如果模型机与原型机满足几何相似、运动相似、动力相似，则两者对应的热力参数和流动参数之比相等，对应的多变效率和损失系数也相等[4-6]。当两台压缩机满足几何相似、进口速度三角形相似、特征马赫数相似和气体绝热指数相等四个条件时，则认为两台压缩机的流动过程完全相似。但在实际工况中，完全相似的情况较少，大多数试验工况与实际工况相比属于第一类或第二类近似相似，即只能满足其中部分相似条件，此时可从部分相似中找出某种联系，再适当补充适当条件，使两机保持近似相似[7-8]。

1.1 第一类近似相似

第一类近似相似是指两种工况条件下，压缩机的绝热指数相等而特征马赫数不相等，即工作介质相同而进口条件不同。特征马赫数不等，说明气体在流道内的参数变化不同，对应的体积比不等，此时无法由进口速度三角形相似推导出叶轮出口速度三角形相似。但如果两者的------M2u相差不大，或------M2u远小于1，则工程上近似认为两者的气体压缩性比较接近，特征马赫数的不等对于气体参数的变化和摩擦阻力系数的影响不大。在满足几何相似、绝热指数相似的前提下，可近似认为叶轮的出口速度三角形也相似。根据相似条件对流量、能头和压比进行换算，公式如下：

式中：Q为体积流量，m3/h；D2为压缩机叶轮出口处的直径，mm；n为压缩机转速，r/min；ε′为压比；m为多变指数；Hpol为多变能头，kJ/kg；Ptot为压缩机轴功率，kW；Rg为气体常数，J/(kg·K)；Ts为入口气体温度，K；ps为入口气体压力，MPa。上标“'”代表实际工况，不带“'”代表厂家的试验工况。公式（1）适用于压比小于2.5的情况，对于压比较高的压缩机，可采用半温升平均比体积法计算。

1.2 第二类近似相似

第二类近似相似是指实际工况与试验工况的气体介质不同，即绝热指数不同。为了使设计条件与实际条件相符，假设压缩机的进、出口体积比保持相等，据此对性能参数进行换算：

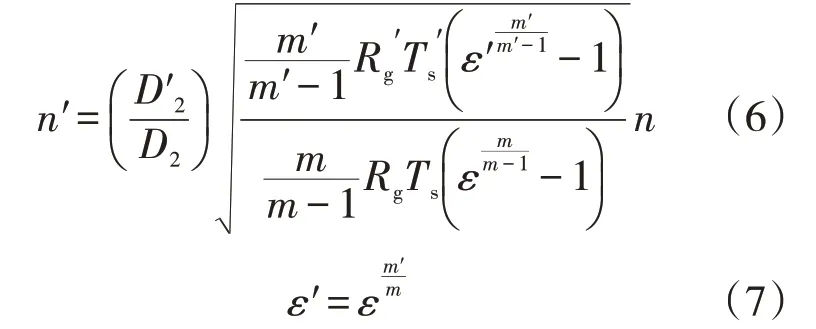
其中，流量、多变能头、轴功率的计算公式与第一类近似相似算法相同，故不进行罗列。

2 基于融合相似原理的压缩机性能曲线研究

应用上述近似原理，可将试验工况和实际工况之间互相转换，但由于是近似相似，故与实际结果之间存在一定误差。为了更好地指导现场操作，将误差控制在较小范围内，首先对两种近似相似算法进行分析，分析影响性能参数计算结果的主要因素。在生产操作中，一般重点关注压缩机出口温度、出口压力和多变能头的变化，其中以上三个性能参数的计算公式均包含压比，说明压比计算结果的准确与否直接关系到压缩机性能参数的换算结果。

对比两类近似相似算法，在求解压比上有明显的不同。对于第一类近似相似，首先假设转速相等，即试验工况与实际工况的转速相等，再根据多变过程推导出式（2）计算压比；而第二类近似相似则完全相反，首先根据压缩机的进出口比体积比保持相等这一条件推导式（7）计算压比，属于等比体积换算，随后根据式（6）确定转速。前者适用于不同绝热指数下的气体和不带冷却系统的压缩机压比换算，而后者适用于两种气体的绝热指数差距不大。前者算法的理论基础更符合热力学过程，而后者算法更符合动力学过程[9-10]，因此前者对于出口温度准确性较高，而后者对于出口压力准确性较高。为了发挥两种算法的优势，将两种算法进行深度融合，提高压比的计算精度，以提高性能曲线的预测精度。

采用改进欧拉法，解决隐式方程在迭代过程中初始值选择不当带来的计算量大的问题。融合相似原理预测流程见图1。

图1 融合相似原理预测流程

利用BWRS方程计算气体的压缩因子、密度、绝热指数等；根据步骤（1）的计算结果，比较两种工况下气体的绝热值，如相等，采用第一类近似相似换算，如不等，采用第二类近似相似换算；利用式（7）计算压比初值，即给定压比的预估值εp-1；利用式（6）确定转速n′，再用式（2）给定压比的校正值εp；将校正值εp与预估值εp-1进行对比，设置两者的误差项δ，如满足＜δ后校正结束，并计算其余性能参数，不满足则重复上述步骤。

3 实例验证

对某输气管道压力站内的离心式压缩机进行实例验证，试验时压缩机的入口气体温度43℃，入口压力6.5MPa，试验气体与实际工况气体组分差异见表1。采用Getdata软件获取不同转速条件下的离散点，分别用第一类近似相似、第二类近似相似和基于融合相似原理的换算方法对压缩机实际性能曲线进行预测，取30组数据与现场传感器的监测值进行对比，不同算法与实际值的绝对误差见图2。

图2 不同算法与实际值的绝对误差（出口温度和出口压力）

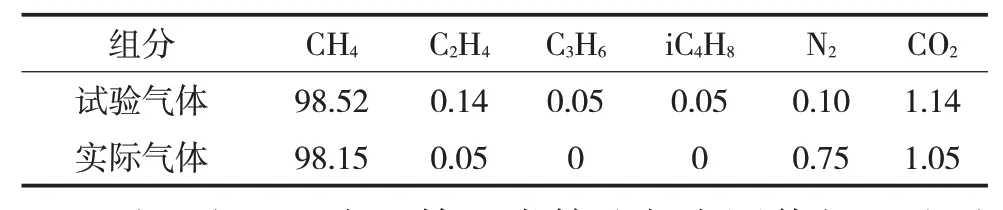
表1 试验气体与实际气体组分差异

对于出口温度，第二类算法与实际值相比绝对误差为3.1～6.7℃，而第一类算法的绝对误差为0.3～2.5℃，可见第一类算法在出口温度的换算上准确性较高，与之前的分析结果相符。基于融合相似原理的换算方法准确度最高，与实际值相比绝对误差仅为0.1～1.8℃，平均相对误差3.32%，满足现场操作的要求。

对于出口压力，第一类算法与实际值相比绝对误差为0.13～0.56MPa，而第二类算法的绝对误差为0.14～0.43MPa，可见第二类算法在出口压力的换算上准确性较高，与之前的分析结果相符。基于融合相似原理的换算方法的准确度最高，与实际值相比绝对误差均在0.11MPa以下，平均相对误差5.17%。

4 应用效果

将修正后的性能曲线代入压气站运行优化方案后，单位距离内天然气的管输单耗及生产能耗进一步下降，在无需其余措施干预的条件下，连续监测20天，压气站运行的整体能耗率平均下降3%～5%，功率下降150～410kW，平均降低功率300kW，性能曲线修正前后的能耗对比见图3，按照目前自用电0.5元/kWh（压缩机组用电）计算，单台压缩机每年可节约成本131.4万元。以一条100km的输气管道为例，在三级地区的管段间隔不超过16km，共设置3～4个压气站，每个压气站设置4台压缩机（基本上为三用一备，或四用无备），则每年可节约成本约1500～2000万元。

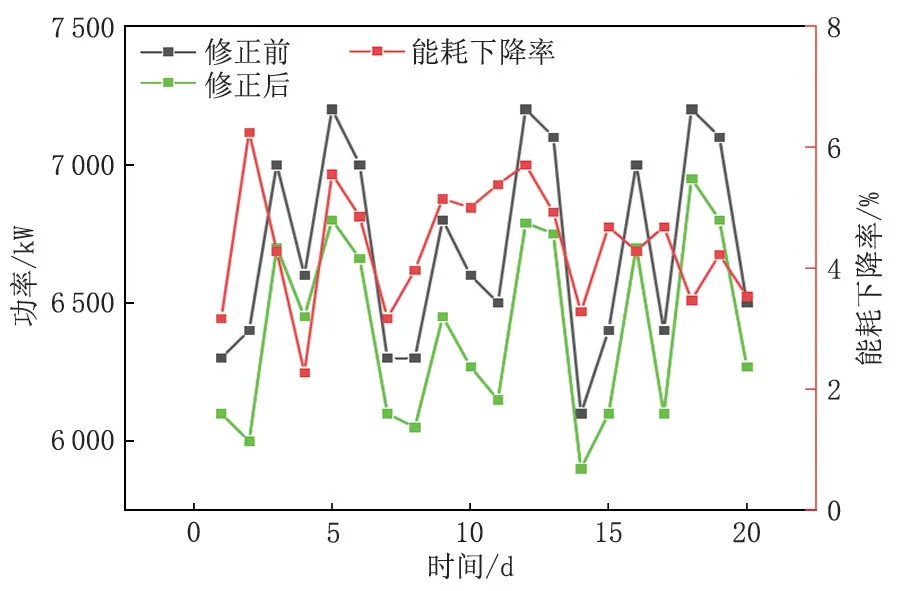
图3 性能曲线修正前后的能耗对比

5 结束语

针对压缩机厂家提供的性能曲线与实际工况下的性能曲线差异较大的问题，通过全面分析和对比两种近似相似原理的不同，在此基础上提出基于融合相似原理的性能参数换算方法，通过实例验证，出口温度和出口压力的平均相对误差分别为3.32%、5.17%，计算精度满足工程需求。