自平衡试桩Q-s曲线理论解析方法研究
欧孝夺,白露,吕政凡,江杰,黄中正
(1. 广西大学土木建筑工程学院,广西 南宁 530004;2. 工程防灾与结构安全教育部重点实验室,广西 南宁 530004;3. 广西金属尾矿安全防控工程技术研究中心,广西 南宁 530004)
自平衡试桩法作为一种新的基桩承载力测试方法,与传统的堆载法、锚桩法相比而言,无需压重平台或锚桩反力装置,可在测试过程节省大量时间、人力及费用,近年来广泛应用于实际工程中确定单桩极限承载力[1−3]。国内外学者对自平衡试桩静载荷试验及应用进行了大量的研究,美国学者OSTERBERG[4]于1989年首先采用自平衡试桩试验对单桩承载力进行测试,而后在欧洲及日本等国得到广泛应用。在我国,最早由李广信教授把该技术引进国内,后由东南大学龚维明团队将此法在国内开始推广与实际应用,并制定相应规范[5−6]。目前,工程中将自平衡试桩测试结果转换为传统静压试验Q-s曲线的方法主要为简化转换法和精确转换法。对于简化转换法行业规范[7]并未对特殊土质或多层地基的转换系数有准确的取值,且相关理论并不完善;而精确转换法需要布置传感器实测桩身加载的各微段内力和位移,增加了试桩的工作量[8−9]。奚笑舟等[10−11]假定桩侧荷载传递规律符合三折线模型,同时桩端桩土作用也符合三折线模型,分别推导出上、下段桩在均质土层和多层地基中的荷载−位移函数解析解,对每层土桩侧摩阻力弹塑性发展规律的多个参数进行拟合,代入解析公式中并结合各土层的连续条件和边界条件得到转换曲线,该法在多层地基中需要拟合各层土的相关参数,造成较大的拟合误差。SEOL等[12−13]在Mindlin 解的基础上,提出一种考虑耦合摩阻力与桩端位移的影响的荷载传递方法;NIAZI等[14]提出一种用于预测自平衡荷载-位移曲线刚度折减模型;王金淑等[15]利用Mindlin 解求出桩侧摩阻力在桩周土体引起的附加应力,建立地下深度基底沉降量的双曲线切线模量法,得到自平衡试桩一种沉降计算理论。上述学者的研究成果集中于试桩荷载传递函数分布规律,但对自平衡法转换过程及方法并未深入研究。综上所述,国内外对自平衡试桩理论研究仍有待进一步完善,对自平衡试桩法的荷载传递机理进行深入研究,求解一种理论转换方法用于自平衡测试确定单桩承载力具有重要意义。本文根据荷载箱对上、下段桩加载的模型,在剪切位移法的基础上,采用理想弹塑性模型分析桩土相互作用,考虑了上段桩自重的影响,利用荷载传递法推导上、下段桩侧理想弹塑性发展规律的轴向荷载传递因子[16],使用MATLAB 编程求得上、下段桩身各微段的侧摩阻力和变位量,代入精确转换公式中,再根据等荷载法将整个试桩转换为传统静压试验荷载-位移曲线,得到单桩极限承载力。最后通过一个工程案例,设置传统静载静压和自平衡试桩两组对比试验,将本文转换方法与传统静压试验结果、简化转换法结果对比,对本文理论方法进行验证,并对该法实用性进行分析。
1 荷载传递函数基本微分方程
根据罗宁[17]对抗拔桩负摩阻力特性的研究,认为桩侧负摩阻力特性也可采用理想弹塑性模型表达,尽管自平衡上段桩侧为负摩阻力,但桩土相互作用与正摩阻力情况是相同的,因此假定上、下段桩土相互作用都为理想弹塑性模型。
根据剪切位移法以及RANDOLPH 等[18]提出的桩土的相互作用机理可假设桩周土的位移为:
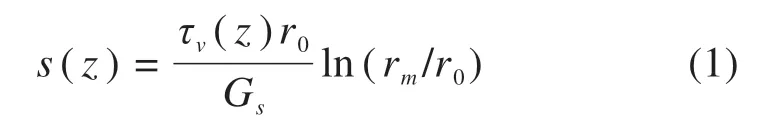
式中:s(z)表示桩身相对位移;τ(z)为z位置处的桩侧摩阻力;r0为桩半径;rm为桩体影响半径,即桩侧土剪切变形可忽略的范围,rm=2.5L(1−vs);L为桩长;Gs为桩侧土剪切模量,Gs=Es/2(1+vs),可根据各层土的弹性模量和泊松比换算关系计算得到;Es和vs分别为各层土体弹性模量和泊松比。对微分单元静力平衡分析:


2 层状地基中自平衡上、下段桩计算方法
2.1 层状地基中上段桩弹性分析方法
由于自平衡试验上段桩身自重一定程度上抵抗桩端加载,因此对试桩微元平衡推导时应计入重力的影响,可得上段桩侧荷载传递基本微分方程:

将试桩按地基土层划分单元,单元厚度为hi,则该土层内试桩单元底部的内力和位移为:

其中:zt=zb+hi,由上式可得试桩单元顶部与底部的内力和位移关系为:

取荷载箱对上段桩加载s1(z)|z=0= 1,则上段桩底加载力可以表示为Q1(z)|z=0=K1s1(z)|z=0=K1,其中K1为上段桩底刚度;此外由于上段桩顶自由端,即加载力Q1(z)|z=L1= 0,根据式(15)及上述边界条件可得上段桩底刚度K1。
所以,对于当给定荷载箱加载值Q1(0),上段桩任一层的桩段位移、轴力可以表示为:

同时,荷载箱安装时预埋的位移杆可测试得到上段桩底的位移,并与上文对桩底位移Q1(0)/K1理论计算值进行对比,可初步检验上述方法其准确性。
2.2 层状地基中上段桩塑性分析方法
当荷载箱加载到一定水平时,上段桩侧土体出现部分塑性区,桩土之间的作用呈现非线性特征。随着荷载箱继续加载,第i桩单元侧摩阻力达到土体抗剪强度τfu(可根据各土层工程勘测结果进行取值)后,假定该单元进入塑性状态后摩阻力保持稳定状态,增加的荷载将转移到上部弹性区的桩单元承担,桩单元i微分方程为:

求解上式可得试桩单元底部与顶部的位移和内力的关系式,将其写成增量的形式为:

2.3 层状地基中自平衡下段桩计算方法
对于下段桩,荷载箱对下段桩加载时,桩侧摩阻力为正摩阻力,加载时不需要克服桩体自重,其受力特征与传统受压桩相同,同理可得桩体微分方程为
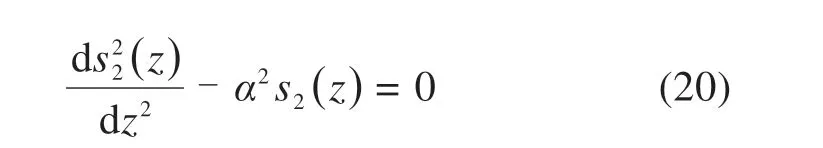
式中:s2(z)和Q2(z)分别表示下段桩身z位置处的位移和轴力。将下段试桩按地基土层划分单元,单元厚度为hi,则该土层内试桩单元顶部与底部的内力和位移关系为:

考虑到桩体各单元内力和位移的连续性可得下段桩顶位移、荷载与桩端位移、荷载的关系为:
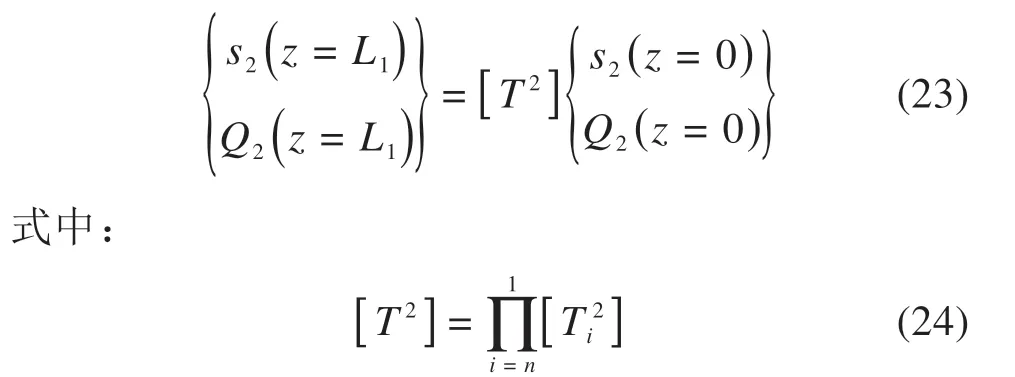
若取荷载箱对下段桩加载位移s2(z)|z=0= 1,同时假定K2为下段桩顶刚度,则下段桩顶荷载箱加载力可以表示为Q2(z)|z=0=K2s2(z)|z=0=K2。而对于下段桩端边界条件,可看作一刚性压块作用于土有P(L) =kbs2(L),其中kb为下段桩端土初始刚度,其值根据Boussinesq公式求得:
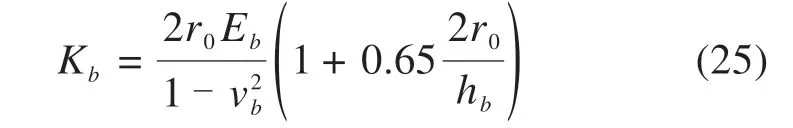
式中:Eb和vb表示下段桩端土体的弹性模量和泊松比;hb表示桩端到基岩的深度。根据式(23)及下段桩上述边界条件可得下段桩顶刚度K2。
因此,对于当给定荷载箱加载值Q2(0)的试桩,任一层的桩段位移、轴力可以表示为:
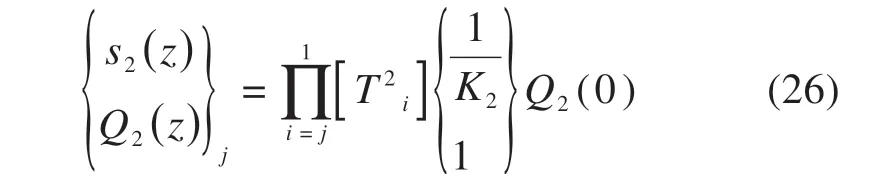
下段桩非线性分析方法与上段桩塑性阶段解析相同,且不用考虑重力的影响,此处将不再详细介绍。
3 转换方法
3.1 精确转换法原理
以荷载箱处为起点,将上段桩分割为n个单元,桩身任意一点i的内力Q(i)和变位量s(i)可用下式计算:

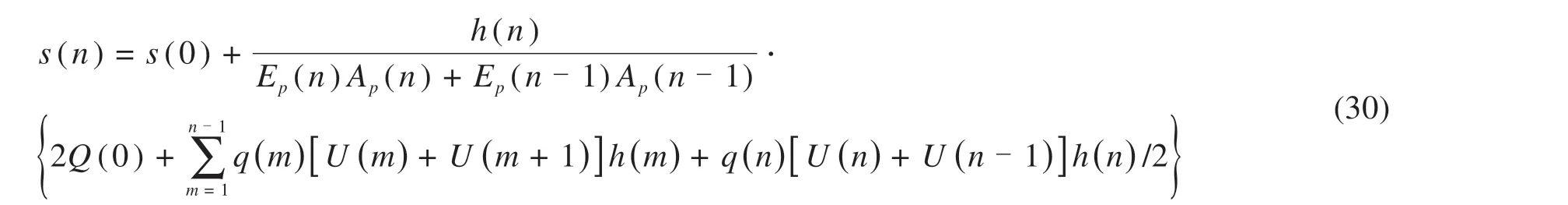
3.2 理论解析转换方法
精确转换法是通过在桩身均匀布置钢筋应变计测试不同深度处的轴力及位移,再代入精确转换公式中将自平衡试桩转换为传统静压荷载的测试结果,而桩身均匀布置应变计这项工作过于复杂,经济性较差,且布置间距相对较大,使得精度降低。而应用上节中自平衡试桩加载的荷载传递模型,采用MATLAB 编程可容易得到多层地基中上、下段试桩沿桩身各处的轴力、位移的数值大小。根据3.1 中自平衡精确转换法原理将自平衡上段桩测试结果进行转换,再利用等荷载法将试桩转换为传统静压试桩对应的Q-s曲线,并求解试桩的极限承载力。


4 实际工程应用与验证
4.1 工程概况
青岛胶州湾大桥位于山东青岛黄海潮州湾[19−20],拟建桥墩桩基在50.00 m 勘察深度范围内,主要由杂填土、黏土、风化角砾岩、弱风化角砾岩等组成。考虑到桥梁桩基需要承受较大的竖向荷载,采用锚桩法和自平衡试桩法来准确测试基桩的承载力,潮州湾地区桥墩桩基位置工程地质条件如表1所示,锚桩法和自平衡试桩法桩体参数如表2所示。

表1 基桩所在土层物理力学参数Table 1 Physical and mechanical parameters of soil layer where foundation pile is located

表2 桩体参数Table 2 Pile testing parameters
4.2 测试方法
使用锚桩法对zh1 试桩进行承载力测试时,采用四锚一的加载系统,6 台液压千斤顶并联加载。使用自平衡法测试试桩zh2 时,各试验装置、荷载箱平衡点位置及土层分布示意如图1所示。沿桩身每隔5 m 均匀布置钢筋应变计和位移传感器,测试各级荷载状态下沿桩身各点轴力及位移的数值。试验加载时采用慢速法逐级加载,每级加载为预估极限荷载的1/10,每级荷载持续1 h,在此期间每隔5,5,10,10,15 和15 min 读取一次数据,而后进行下一级加载。根据《建筑桩基技术规范》[7]当荷载或位移达到规定值时终止加载。
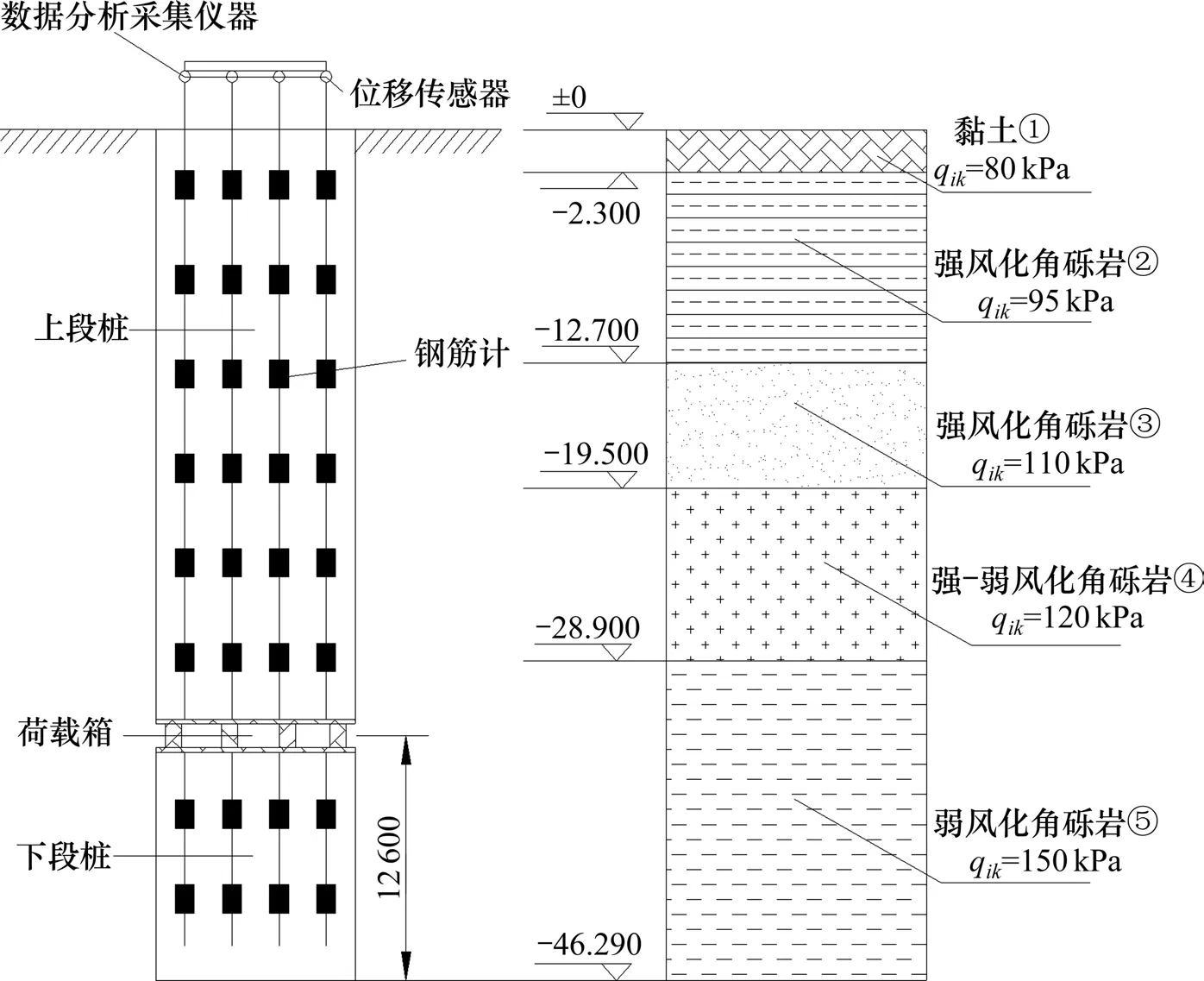
图1 自平衡法测试及土层示意图Fig.1 Self-balanced test and soil layer distribution diagram
4.3 试验结果
4.3.1 试桩Q-s曲线
锚桩法得到传统静压桩顶荷载-沉降曲线如图2。锚桩法加载时,根据桩的极限承载力估算值38 000 kN,将荷载分为13个等级,每级3 000 kN。桩顶累计位移15.30 mm,加载前期位移随着荷载缓慢增加,当荷载加载到33 000 kN 时桩顶位移为6.93 mm,且有明显增大趋势,继续加载至36 000 kN时桩顶位移已达到9.42 mm,其增加量已大于前一级加载作用下位移增量的2倍,可判定试桩已发生破坏,取34 055 kN 为锚桩法静载试桩极限承载力。
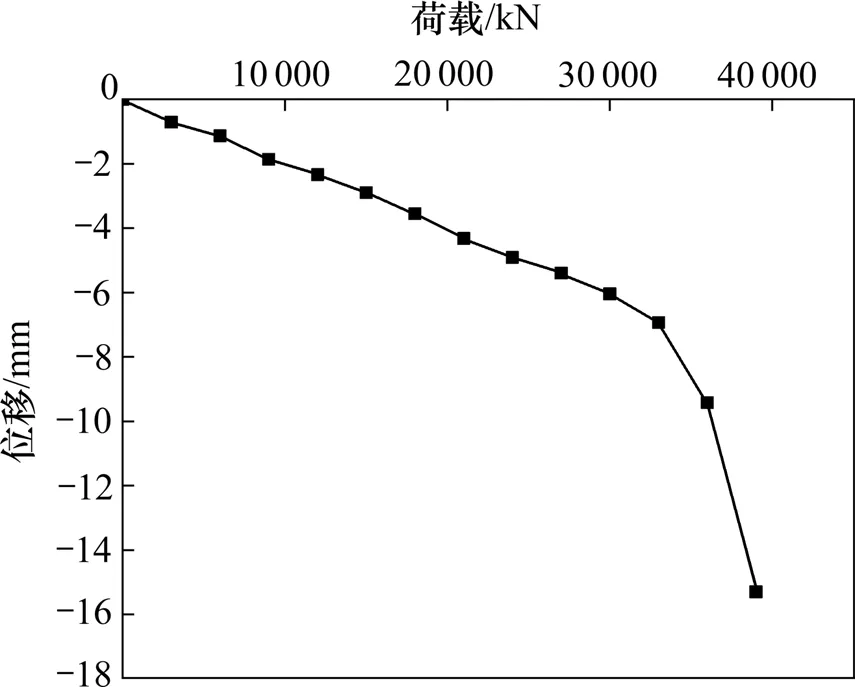
图2 传统静压桩Q-s曲线Fig.2 Q-s curve of traditional static pile
利用自平衡法测试得到上、下段桩荷载-沉降曲线如图3所示。在自平衡法试验中,上段桩顶与桩底Q-s曲线发展趋势基本相同,加载分为15个等级,每级加载1 500 kN,荷载箱逐级加载直至破坏,负荷情况正常。加载至2×16 500 kN(上、下段桩同时加载)时,向上位移约9.91 mm,向下位移约8.84 mm,二者均较小,继续加载为2×18 000 kN时,向下位移13.22 mm,可见下段桩位移已达到增加量已大于前一级加载的2倍,可判定下段桩桩已发生破坏,当继续加载至2×19 500 kN,上段桩桩底位移15.68 mm,可判定上段桩加载已达到极限载荷,即停止加载。取上、下段桩极限承载力分别为18 771 kN和16 436 kN。
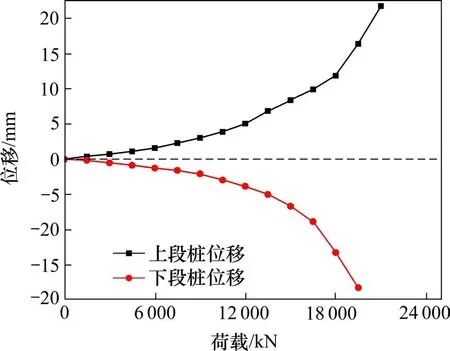
图3 自平衡试桩Q-s曲线Fig.3 Q-s curve of self-balanced pile test
4.3.2 桩身轴力分析

式中:Nij第i级荷载第j段桩身轴力;εij第i级荷载第j段桩身应变值;Ep为桩身弹性模量;Ap为第j段桩体截面面积。
在上述自平衡加载工况下,对荷载箱加载值理论解析计算出对应桩身各点处的轴力,同时在桩身布置应变计测得桩身不同埋置深度应变值,并通过式(32)计算得出桩身不同深度处轴力,分别取加载值为4 500,9 000,13 500,16 436 kN(下段桩承载力)和18 771 kN(上段桩承载力),且离加载点位置向上为正距离,向下为负距离,各级加载下桩身各点轴力计算值与实测值对比如表3 所示,绘制出轴力分布对比如图4所示。可以看出各级荷载的理论计算结果与实测结果均比较吻合,对于下段桩,加载力身下部轴力衰减较大,表明当荷载较小时,所施加荷载主要由桩身下部土层承担,随着荷载增加,上部土层逐渐发挥作用。从线形疏密程度来看,曲线越疏轴力衰减越大,上段桩从加载点0~15 m 长度范围曲线较疏,衰减量为46.67%~60.85%,表明该部分土层承担的荷载较大。另外,上段桩与下段桩在离加载位置相同处的轴力曲线基本重合,轴力随荷载变化与加载方向无关。

表3 每级加载下桩身各点轴力计算值与实测值对比Table 3 Comparison of calculated and measured values of axial force at every point of pile under each stage
4.3.3 桩身侧摩阻力分析
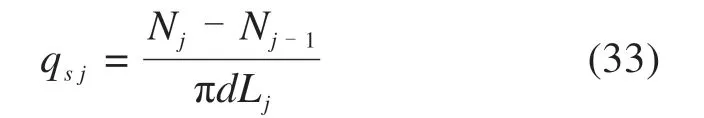
式中:qsj为第j段侧摩阻力;Nj,Nj-1为第j,j-1 段轴力;d为桩直径;Lj为第j段桩身长度。
整理图4 中的轴力计算数据,根据式(33)通过相邻测点的轴力之差除以相应的侧面积得到的平均侧摩阻力,并把这个平均侧摩阻力作为2个测点中点处的侧摩阻力值,依次连接各中点得到平滑的曲线作出桩身侧摩阻力分布曲线如图5所示。可以看出,各级加载作用下的理论计算结果与实测结果均比较吻合。此外,自平衡上段桩侧摩阻分布呈下大上小特征,随荷载增加,桩身各位置侧摩阻均增大,摩阻力增量从桩身下部往上逐渐减小。在加载位置附近,侧摩阻最先开始发挥,达到一定应力水平后,桩顶侧摩阻接近极限值,并出现弱化,随着荷载增加,桩身中下部土层摩阻力逐渐发挥。上段桩曲线类似双曲线形,上段桩桩侧摩阻力在桩端(2.0 m)处出现峰值,并出现软化,只有在桩底附近桩侧摩阻力呈缓慢增长趋势。

图4 自平衡试桩各级荷载下试桩轴力分布图Fig.4 Axial force distribution of self balanced test pile under different loads

图5 自平衡试桩各级荷载下桩侧摩阻力分布图Fig.5 Distribution diagram of lateral friction resistance of self-balanced pile under various loads
4.3.4 等效转换结果
将上述理论求得极限荷载下桩身各点侧摩阻力和变位量代入式(29),并将其和下段桩加载数值代入式(31),利用等荷载法求得上、下段自平衡测试等效转换Q-s曲线,同时锚桩法求得传统静压桩实验结果以及自平衡试桩精确转换法、简化转换法(转化系数为0.87计算)对比结果如图6所示。

图6 不同转换方法与锚桩法Q-s曲线对比图Fig.6 Comparison of Q-s curves between different conversion methods and anchor pile method
从图6可以看出,针对多层地基中自平衡静载试验解析转换法与简化转换法而言,本文解析转换法Q-s曲线吻合效果更优于简化转换法。利用本文理论解析方法求得极限承载力为34 265 kN,而使用简化转换时,分别取上、下段桩的极限荷载,可得承载力为35 534 kN。可见与多层地基中自平衡静载试验解析转换法与简化转换法相比,本文转换法Q-s曲线吻合效果更优于简化转换法。对单桩承载力而言,本文方法所求解的单桩承载力更接近与传统静压试验和精确转换法解得承载力,而简化转换结果偏大,相较于简化转换法,其精度提高12.3%。
5 结论
1) 通过青岛胶州湾大桥工程基桩承载力锚桩法和自平衡法测试实例,对本文理论解析方法进行验证,与传统静压静载荷试验以及简化转换法对比表明,本文理论解析方法与锚桩法实测传统静压试验的Q-s曲线结果吻合效果较好,可见本文方法有一定的可行性与适用性,同时相比简化转换法精度有很大的提高,证实了本文解析转换法的准确性。
2) 本文转换法与工程中精确转换法相比,无需布置传感器,具有完整的理论基础,通过实际工程验证表明,推导的解析公式能较好地反映自平衡试桩上、下段桩的荷载沉降特性以及桩侧摩阻力和桩身轴力分布规律,因此本文转换方法具有一定的经济性和高效性,可在自平衡试桩确定基桩承载力工程中得到不断的应用。
3) 本文对多层地基中自平衡试桩荷载传递理论解析进行了分析,该法亦适用特殊地层和变截面扩底桩承载力测试,同时需设置更多的室内对比试验及工程案例来分析验证自平衡试桩单桩承载特性,这是下一步需要深入研究的内容。

