基于小闪烁室测氡仪快速定值方法研究

王政霞， 李志强， 李彦秋， 张书燕， 徐 勇， 李 磊

(衡阳师范学院， 衡阳 421002)

氡是公众所受天然辐射最主要的来源之一，约占总剂量的55%[1]. 氡浓度的可靠测量可为辐射防护和环境保护提供参考依据[2].高探测效率且受湿度影响小的闪烁室测氡法是氡测量的主要方法[3]. 此方法为了保证氡的总活度变化不超过1%，取样结束后需要静置3 h使氡及其子体达到平衡才可测量[4-7]. 这不利于快速跟踪氡浓度变化的测量[8]. 为了缩短测量时间, 可在氡及其子体建立平衡前计数. 本文通过积分计数法根据氡及其子体原子数的衰变关系，建立了不同测量周期的氡浓度刻度因子计算方法，实现闪烁室氡浓度的快速定值; 在Rn-222、Po-218和Bi-214的探测效率相同的条件下，利用54 mL的小闪烁室在氡浓度为20 Bq/mL的条件下对闪烁室测氡仪开展快速定值研究.

2 快速定值原理

闪烁室内氡及其子体的原子数变化满足递次衰减规律. 根据氡及其子体简化衰变链规律, 可依次得到Rn-222、Po-218和Bi-214的放射性活度. Po-218、Bi-214的半衰期远远短于Rn-222的半衰期，在取样过程中视闪烁室内氡浓度不变，且在T=0时闪烁室内氡气是均匀分布的. 图1为氡及其子体简化衰变链.

图1 氡及其子体简化衰变链Fig.1 Simplified decay chains of radon and its daughters

设在时刻T内Rn-222、Po-218和Bi-214的原子核数分别为NR、NP和NB，在初始时刻T=0时测量腔内无子体，即取样完成后只有氡. 设测量周期为T，取样时间为Ts，依据被收集的α粒子数与不同测量周期的刻度因子关系式来确定氡浓度. 小闪烁室测氡仪Rn-222浓度测量公式为[7]

CR=KΔNA(T)

(1)

式中CR为被测环境氡浓度；K为小闪烁室刻度因子；△NA(T)为不同测量周期的Rn-222、Po-218和Bi-214进一步衰变产生的总α粒子计数. 小闪烁室收集到的α粒子数与Rn-222、Po-218和Bi-214的关系如下.

NA=NR+NP+NB

(2)

式中NA为小闪烁室的净计数率，NR、NP、NB分别代表Rn-222、Po-218和Bi-214衰变产生的α粒子数. Rn-222、Po-218和Bi-214的放射性活度AR、AP、AB随时间的变化满足下列方程[9].

AR(t)=CRVe-λRt

(3)

(4)

AB(t)=CRV[h1e-λRt+h2e-λPt+h3e-λbt+

h4e-λBt]

(5)

其中

式中λR、λP、λb、λB是Rn-222、Po-218、Pb-214和Bi-214的放射性半衰期(min-1)；CR是闪烁室中初始氡浓度(Bq/m3)；V是闪烁室体积(L). 在Ts～T+Ts时间段内小闪烁室测得的α粒子数为

(6)

式中ηR=ηP=ηB[10]；Ts为采样时间.将上式简化并积分为

(7)

令

(8)

已知T0时刻与不同测量周期Tx的氡浓度相等，K0与Kx关系式应满足如下关系

CR=K0NA(T0)=KxNA(Tx)

(9)

式中Tx为不同周期的测量时间；Kx为不同测量周期Tx的刻度因子；K0为60 min的测量周期刻度因子. 将式(9)转换则得到不同测量周期的刻度因子与60 min的测量周期刻度因子的关系为

(10)

根据图1已知λR=0.000 126，λP=0.227 261，λb=0.025 864，λB=0.035 185[3]，将其代入式(10)中，得到不同测量周期的刻度因子公式.

(11)

将Kx代入式(1)中即可得到氡浓度计算公式为

(12)

式(12)为不同测量周期对应平衡时的氡浓度计算公式. 由不同测量周期的总α粒子数和刻度因子的乘积即可得到平衡时的氡浓度. 为了确定刻度因子公式的正确性，采用固定氡浓度对60 min、30 min和15 min的刻度因子进行计算，再利用小闪烁室对其进行验证.

3 定值实验方案

实验装置主要由小闪烁室、FD125氡钍分析仪和定标器组成，实验验证装置如图2所示.

图2 实验验证装置图Fig.2 Experimental verification device diagram

根据氡及其子体的衰变关系, 运用积分计数法计算不同测量周期的刻度因子时必须满足两个条件：(1) 用给定样品在给定计数瓶中进行实验时，效率必须保持恒定；(2) 样品在进入计数室时必须不含子代[11]. 为减少计数误差，满足小闪烁室对氡及其子体衰变产生的α粒子的探测效率近似达到100%，即“ηR=ηP=ηB”，将容积为54 mL的小闪烁室分为八等分圆柱体，且满足两个条件：(1) 小闪烁室内任意两点间的距离小于Rn-222及其子体衰变释放的α粒子的射程；(2) 小闪烁室内表面及有机玻璃隔板需全部均匀涂上ZnS(Ag)[9，12].

本文选取浓度为20 Bq/mL的氡源作为标准氡浓度，小闪烁室的体积为54 mL，实验环境温度12～21 ℃，标准大气压. 为减少计数误差，需保证氡及其子体衰变释放的α粒子产生的光电信号均能被记录. FD125氡钍分析仪工作高压设置为-539 V. 首先用泵抽取真空清洗小闪烁室内上次测量残留的氡及其子体，使室内本底降低后再利用FD125氡钍分析仪测得其值. 然后选用容积为1 mL的针管抽取1 mL氡源过滤完再注入真空小闪烁室中. 松开橡皮管上的夹子使小闪烁室内的氡在空间内平衡再夹住，此时小闪烁室内氡浓度变为3.7×105Bq/m3.

采样结束后将小闪烁室放入FD125氡钍分析仪中，设置定标器的采集时间和次数，测量不同周期的氡及其子体衰变产生的总α粒子数NA. 将T0=60 min时的总α粒子数代入式(1)即可计算得到刻度因子K0值. 根据K0值和式(11)可计算得到不同周期的刻度因子.

用FD125氡钍分析仪测量T0=60 min时小闪烁室内氡及其子体衰变产生的总α粒子数，重复测量10次再求平均值. 将氡源标准浓度代入式(1)得到刻度因子K0值, 再依据式(11)得到K30和K15的值. 将用定标器得到的NA值代入式(12)，验证快速定值的结果.

小闪烁室标准浓度为3.7×105Bq/m3. 为了满足积分计数法的两个必要条件, 利用真空泵清洗小闪烁室后测量其本底, 以免对实验结果产生影响. 氡源经过滤后再注入测量腔中，将小闪烁室对准FD125氡钍分析仪的光电倍增管上端, 记录氡及氡子体衰变产生的总α粒子计数，连续测量10次周期为60 min的总α粒子计数[13]. 将氡标准浓度作为参考浓度, 代入式(1)得到刻度因子K0值, 结果如表1所示.

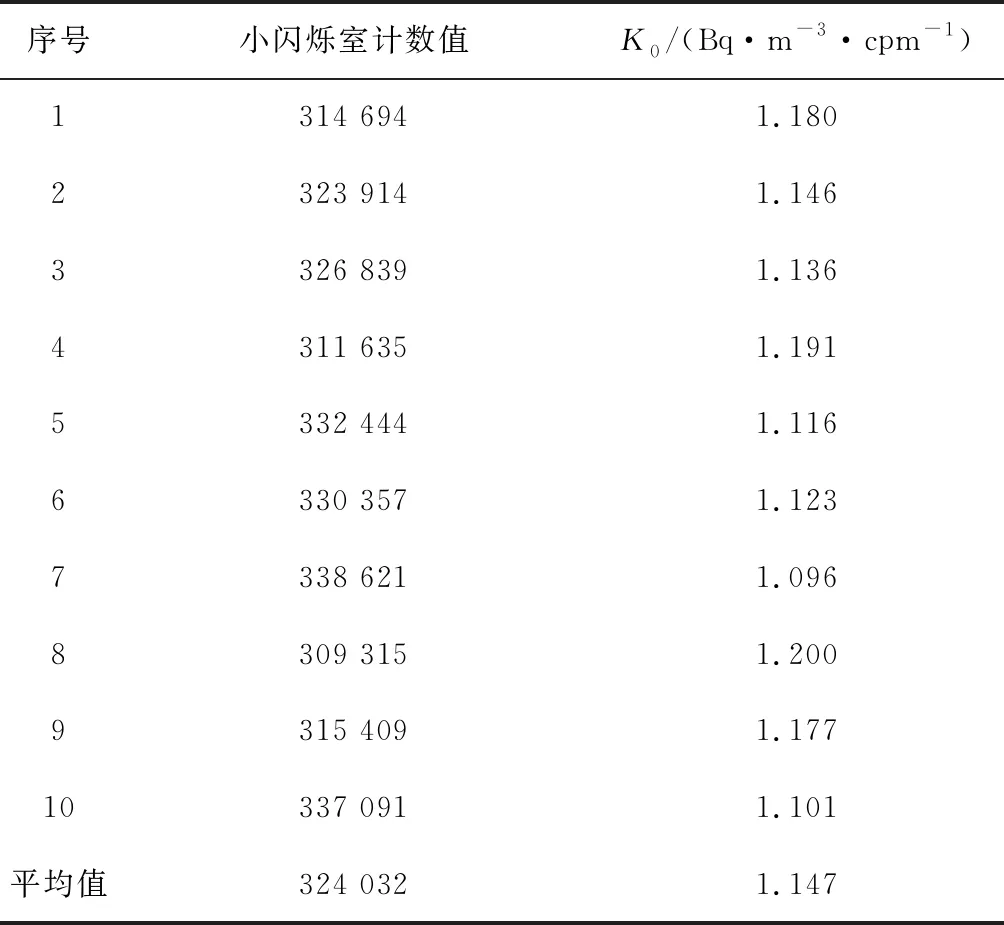
表1 K0的测试结果

10次测量的数据存在差异，这是因为闪烁室内本底波动、人工采样的不准确性、温度波动较大和α衰变的随机性导致的. 但是总的来看波动较小，这是统计涨落的结果，表明数据符合放射性规律. 为减少温度等因素带来的计数误差，采取平均值计算结果. 在计算时需要修正上一次测量残留的氡子体衰变产生的计数，其本底平均计数为17 cpm. 由表1可知, 在周期为60 min的条件下, 10次的总α粒子计数平均值为324 032，小闪烁室修正后的相对标准误差RSD为3.3%. 由式(1)计算可得平均K0值为1.147 Bq·m-3·cpm-1.

设置测量周期为30 min和15 min，根据上述得到的K0值和式(11)即可计算不同周期的刻度因子，分别为K30=2.481 Bq·m-3·cpm-1，K15=5.226 Bq·m-3·cpm-1.

将20 Bq/mL标准氡源抽样1 mL至小闪烁室中，用FD125氡钍分析仪记录氡及其子体衰变产生的总α粒子计数，连续测量10次周期为30和15 min的计数. 利用式(12)计算不同测量周期的氡浓度值. 表2和表3是周期为30和15 min的测量结果. 其中K30ex和K15ex为实验所得刻度因子，将α粒子计数代入式(1)即可得到K30ex和K15ex.

表2 30 min周期的测量结果

由表2可知，在测量周期为30 min时经过修正后小闪烁室的总α粒子计数平均值为150 523，其相对标准误差RSD为2.42%.依据式(1)得到其平均刻度因子K30ex为2.464 Bq·m-3·cpm-1，相对标准误差为2.42%，且与理论刻度因子K30的误差在4%以内，表明在30 min时理论刻度因子计算公式是可行的.

由表3可知，测量周期为15 min时经过修正后小闪烁室的总α粒子计数平均值为71 193，由式(1)得到其平均刻度因子K15ex为5.217 Bq·m-3·cpm-1.由于环境温度、气压和人为等因素引起计数落差，但总α粒子计数相对标准误差RSD为1.84%，实验刻度因子K15ex的RSD也为1.84%.

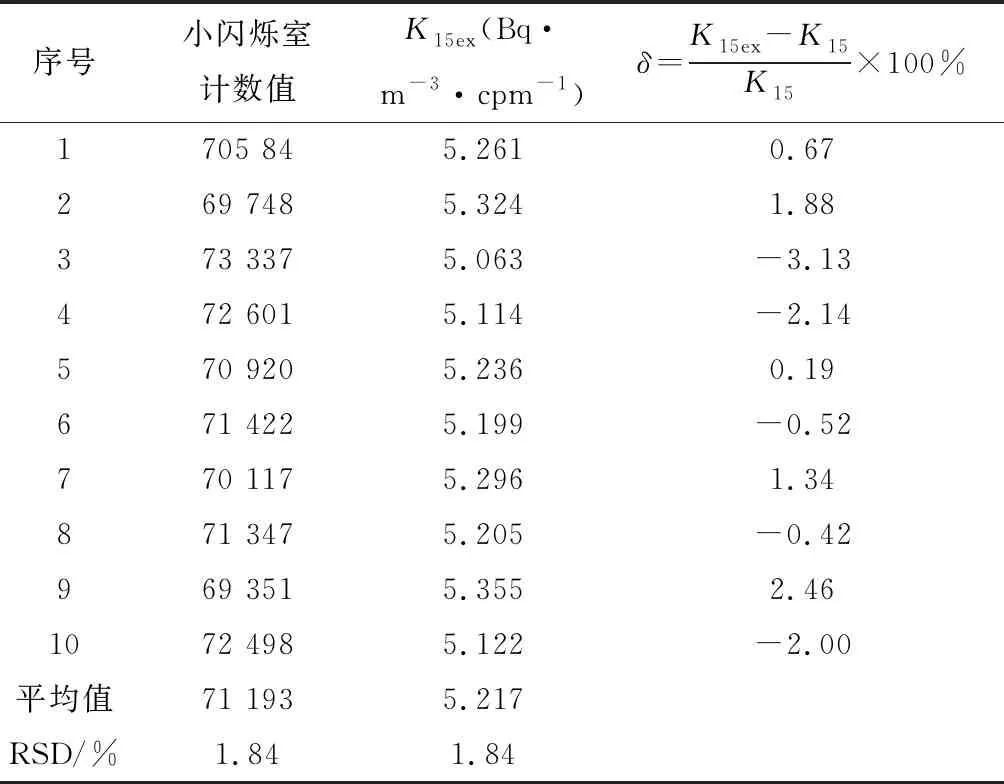
表3 15 min周期的测量结果

从上述实验数据来看，对于氡浓度为3.7×105Bq/m3时理论K值与实验K值误差在4%以内，证明在高氡浓度条件下利用快速定值方案缩短测量时间是可行的.

5 结 论

本文用积分计数法研究小闪烁室的快速定值方法对氡浓度进行快速测量，理论刻度因子K30和K15的值分别为2.481和5.226 Bq·m-3·cpm-1；利用小闪烁室对浓度为3.7×105Bq/m3的氡源进行探测，根据测得的α粒子计算实验刻度因子，理论计算值与实验验证值误差在5%以内，表明小闪烁室快速定值方法是可行的. 上述定值方法对于容积为500 mL的大闪烁室，在确定其探测效率后也同样适用.