基于区域失衡子空间的领先NSGAII算法
甘翔宇, 周新志, 杨秀清, 向 勇, 叶 毅
(四川大学电子信息学院, 成都 610065)
1 引 言
现实生活中的很多工程和科学问题,在决策过程中都涉及到多目标优化问题(Multi objective Optimization Problem, MOP),例如多机器人任务分配(Multi Robot Task Allocation, MRTA)问题[1]、资源受限的项目调度优化问题(Resource Constrained Project Scheduling Optimization Problem,RCPSP)、基于多目标路径规划的资源配置问题等. 在这些问题中,目标函数之间经常是冲突的、相互制约的. 传统多目标优化问题求解方法有加权法[2]、约束法和目标规划法等,这些方法的基本思想大多是把多目标问题中的子目标函数,经过处理转换为单目标问题,通过对单目标问题求解达到对多目标函数的求解. 而现实中MOP的目标函数、约束函数大多是非线性、不连续的,传统的优化方法效率低,因此对有效的进化优化算法的研究是十分必要的.
在众多多目标优化算法中,Deb在2002年提出的NSGAII算法[3]是影响最大和应用范围最广的,该算法具有较低的计算复杂性且在相同时间内能获得较优的求解性能. 但NSGAII算法作为一种类随机搜索算法,存在收敛速度慢和解分布特性差的问题. 针对NSGAII算法收敛性不足的缺陷,陈辅斌等[4]引入了免疫平衡原理,改进NSGAII算法的选择策略和精英保留策略,避免了局部收敛问题. Mithilesh等[5]将涉及最佳染色体组的初始随机种群的改进库纳入多目标优化算法的框架,以最小的世代数提高了收敛到全局Pareto最优前沿的速度. Ahmadi等[6]研究了MAP在NSGAII算法中的集成,实现了收敛性的提高. 为解决NSGAII拥挤度距离机制无法有效区分多样性个体的缺陷,崔志华等[7]提出了基于平均距离聚类的NSGAII. 文献[8,9]将动态拥挤距离(DCD)和受控精英(CE)引入NSGAII,提出的算法在维持多样性方面表现优于NSGAII. 王明昭等[10]基于均匀聚集区间和基尼权重构造了一种均匀聚集距离算子,使所求解集更好、更均匀地收敛于Pareto最优边界. 为进一步提升算法的性能,还有许多研究者尝试把局部搜索思想融入到NSGAII算法中. Lara等[11]提出一种用于多目标模因算法的新的局部搜索策略. Harada等[12]提出将梯度信息用于局部搜索过程,根据梯度信息找到向Pareto最优前沿收敛的方向,从而提高收敛速度和精度.
基于收敛性和多样性这两个多目标优化问题中的关键性能指标,本文提出一种基于区域失衡子空间的领先NSGAII算法(Leading NSGAII Algorithm based on Regional Unbalanced Subspace),实现种群快速接近Pareto前沿并有良好分布性. 种群进化前期优先在领先解个体周围搜索,可避免随机搜索过程计算量大的问题,提高算法运行效率,使种群快速收敛;由于迭代过程中种群分布不均会导致多样性变差,容易陷入局部最优,因此该算法提出区域失衡子空间概念,通过均匀划分目标空间,改善失衡区域来减少局部搜索计算量,提高解的质量,使解的分布更符合真实前沿的形状. 最后通过基准多目标优化实验验证算法的有效性.
2 基本定义
本文主要针对多目标优化问题,其中相关定义解释如下.
定义1多目标优化问题MOP. 具有n个决策变量,m个目标函数的多目标优化问题通常可以描述为
minimizeF(x)={f1(x),f2(x),...,fm(x)},
x=(x1,x2,...,xn)T∈D⊂Rn,
li≤xi≤ui,i=1,2,...,n
(1)
式中,x表示n维决策变量;F(x)⊂Rm为m维目标向量;D⊂Rn表示n维决策空间;fj(x)(j=1,2,...,m)为第j个目标函数;li和ui分别为第i个决策变量xi的下界和上界. 在不失一般性的前提下,假设f1(x),...,fm(x)将被最小化,因为最大化问题也可通过对偶原理转化为最小化问题.
定义2Pareto支配. 对于任意决策向量,若满足以下条件.
(2)
则称xu支配xυ,或称xu相较于xυ占优,记xuxυ.
定义3Pareto最优解. 多目标优化问题中优先考虑的一组折中解决方案,无法比较各个目标函数的优劣性,即不能保证在改进一个目标函数的同时不削弱至少一个其他的目标函数,即Pareto最优解.
定义4Pareto最优解集. 决策空间中Pareto最优解的集合构成了Pareto最优解集(PS).
PS={xu∈D|∃xυ∈D,xυxu}
(3)
定义5Pareto最优前沿. Pareto最优解集对应于目标空间中的像集称为Pareto最优前沿(PF).
PF={F(Xu)=f1(xu),...,fm(xu)|xu∈PS}
(4)
3 NSGAII-URS算法
NSGAII是一种带有精英保留策略的快速非支配多目标优化算法. 该算法降低了非劣排序遗传算法的复杂性,但NSGAII算法仍然存在搜索随机性偏大、收敛速度慢和解分布均匀性较差的问题. 因此本文提出在NSGAII算法基础上,在种群进化前期,根据解的优劣性求得当前非支配解中的领先解,并加入到领先解解集,通过在领先解周围局部搜索来加快算法收敛速度. 同时为了避免算法陷入局部最优,本文提出将目标空间均匀划分为一系列子空间,结合基于稀疏度的局部搜索策略来分别优化不同的失衡区域,从而改善种群分布不均现象. 下面对NSGAII-URS算法其中涉及的优化方法和策略进行详细的描述.
3.1 算法框架
算法1描述了NSGAII-URS算法的主要框架,首先,初始化种群PI,种群数量为N,从中选择优秀个体进入交配池;然后,采用模拟二进制交叉和多样式变异产生子代PM; 再通过对领先解进行局部搜索得到领先局部解PL,再对失衡子空间进行优化获得失衡局部解PB,将领先局部解和失衡局部解统称为局部解PN,将子代和父代以及局部解合并得到新父代PO;最后,通过环境选择机制从新父代中选择最优N个个体进入下一代,重复以上步骤直到满足终止条件.
在NSGAII-URS算法中最大进化代数的2/3被作为种群进化中使用两种不同策略的分割点.这是因为整个进化过程共分为进化前期、中期和后期三段,每一个进化段长度为1/3总迭代数. 由于对领先解集进行局部搜索操作偏向于强调解的收敛性,容易忽略多样性和分布均匀性,而且种群进化到后期收敛性已经基本得到优化,因此本算法在后期将不再对领先解集进行处理.
3.2 领先解集
NSAGII算法通过个体之间的支配关系对种群中的个体进行排序,下一代种群选择时,先从最高级别的非支配解(FrontNo=1)中进行选择,以此加快算法的快速收敛. 由于非支配解也会存在明显Pareto前沿倾向的个体,因此本文在文献[13]提出的超平面辅助思想的基础上,定义了当前非支配解中的领先解集.该集合中的领先个体将作为每轮迭代过程中的重点搜索对象,引导种群更快收敛至Pareto真实前沿.
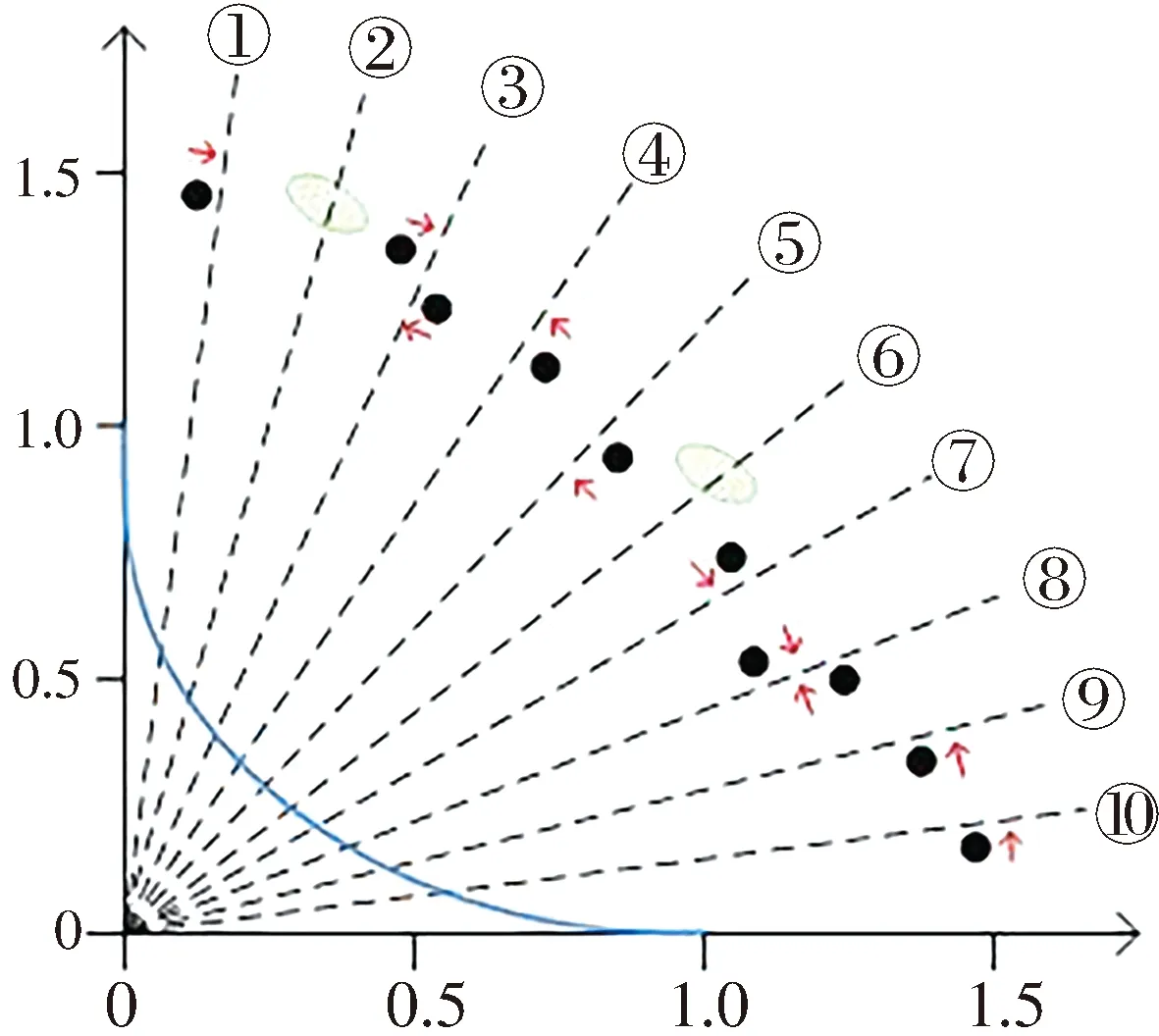
超平面辅助思想是用个体周围的相邻解构成的超平面,在非支配解中区分出对Pareto最优前沿有明显倾向的个体. 对于具有m个目标的个体,其相邻解决方案集定义为B(xi)={xi1,xi2,...,xim},当fm(xi) 算法1 Framework of NSGAII-URS InputN(种群规模),IMAX(最大进化代数) OutputPOMAX(最终种群) 1) Initialize the populationPwithNrandom individuals 2) while NotTerminate(Population) do 3) MatingPool= T-Select(PI) 4)PM=GA(Population(MatingPool)) 5) ifi<(2/3)*evaluationthen 6)PN= LocalSelection1(PI(F=1)) 7)PO=PI+PM+PN 8)PO+1= E-Select1(PO) 9)O= O+ 1 10) else 11)PU= LocalSelection2(PI(F=1)) 12)PO=PI+PM+PU 13)PO+1= E-Select2(PO) 14)O=O+ 1 15) end 16) end 17) returnPO+1 虽然对领先解的操作可促进种群收敛,但只关注领先解可能会导致种群陷入局部最优,还需重点优化解的分布均匀问题. 传统NSGAII算法提出的拥挤距离和拥挤度比较算子不能有效保持种群多样性,因此有研究者提出将局部搜索策略与NSGAII算法结合,但局部搜索过程会产生大量局部解,使计算量成倍增加. 因此,本文提出基于每轮迭代非支配解区域失衡概念,在每次遗传过程中对目标空间中的不均匀解进行局部搜索,从而有效减少遗传过程中的计算量,保持种群多样性和均匀性. 图1 领先解示意图 3.3.1 失衡子空间 文献[14]将当前非支配解中稀疏度最小的作为稀疏解,通过在稀疏解周围搜索以减少局部搜索过程的计算量. 该思想的优点在于当解分布不均匀时,在稀疏解周围局部搜索,当解分布均匀时,最边缘的解稀疏度最小,从边缘开始向外搜索,可以增加解集的广泛性. 但在一次迭代过程中仅对一个稀疏解进行局部搜索操作并不能有效改善解的均匀性.因此本文将重点关注目标空间中的非支配解所在区域,在每次求解过程中将目标空间均匀分区,在各子空间中划分当前非支配解,当存在失衡子空间时,采用不同的策略来改善局部子空间失衡情况. 失衡子空间的优化过程如算法2所示,首先使用一组单位向量将目标空间划分为一系列子空间,如下所示. U=(u1,...ui,...,uk) (5) V={v1,v2,...,vk} (6) H={H1,H2,...,Hk} (7) Hj=(ue,...,uw) (8) 其中,U为每轮迭代非支配解的集合;k为非支配解的个体数量;V为一组单位向量,将作为参考向量来划分失衡区域;H为均匀划分的子空间;Hj为第j个子空间内所包含的个体,ue、uw∈U. 判断失衡子空间的方法如下.对于每个非支配解ui,首先需要将其与各子空间关联,计算其与各参考向量vi之间的夹角余弦距离,通过排序比较,得到与之最近的参考向量的序号,即分别划分给不同的子空间,依靠划分结果可以判断失衡子空间. 如图2所示,虚线所对应的参考向量将目标空间均匀划分,以此为基准可将这片区域抽象为子空间集{Hr1,…,Hr10},如图2箭头所示,根据计算结果,每个解都求得与之对应的参考向量,即分别与子空间建立了联络. 通过区域划分确定了失衡子空间,分为以下两种情况. 情况1某些子空间可能没有解,例如Hr2、Hr6,定义该类空间为空闲子空间. 情况2某些子空间可能有多个解,例如阴影区域所示的Hr3和Hr8. 其余子空间相较于Hr3和Hr8具有更少的解,定义该类空间为稀疏子空间. 根据以上划分,判断本次遗传过程中种群分布并不均匀,子空间存在失衡现象. 根据子空间的状况分别采取不同的处理方法. 对于稀疏子空间,可以在下一轮迭代中对该空间内的个体进行局部搜索;对于空闲子空间,可以分别选取离该区最近的个体通过极限变异策略得到非均匀解. 局部搜索策略将在下节中进行详细的描述. 算法2 LocalSelect1 InputPI(F=1),I(进化代数) OutputPN(局部解) 1) Initialize a set of unit vectorsV={v1,…,vk} 2) Normalize the current non-dominated solutionPI(FN=1), denote the normalized matrix as Objs Objs=(Objs-Zmin)/(Zmax-Zmin) 3) Ang=ACDis(Objs,V) 4)nn=unique(min(Ang)) 5)l1=[1:len(PI(F=1))] 6) fori=1 len(nn) do 7) mm=(l1-nn(i))==0 8)l1(mm)=[] 9) end 10)l2=l1calculate the subspace that’s not allocated to the individual 11) fori=1-length(l2) do 12) execute extreme optimization mutation strategy 13) end 14) returnPN 图2 失衡区域示意图 3.3.2 基于稀疏度的局部搜索策略 (1) 稀疏子空间.对于该类子空间,选取该区域内稀疏度最大的个体,通过在该个体周围局部搜索来增强该区域的多样性.其中稀疏度的计算公式如下. 设第i个解的目标向量为(f1(Xi),…,fm(Xi)),对函数值进行归一化处理. (9) 其中,fjmax和fjmin分别是当前所有解对应的第j个目标函数值得最大和最小值. 归一化后第i个解Xi的稀疏度计算公式为 (10) 其中,ni为目标空间中与目标向量F(Xi)欧氏距离小于r的其他目标向量的个数;r的取值范围为0 (2) 空闲子空间.由于本次迭代中该区域内未分配到个体,因此对距离该区域最近的两个个体采用极限优化变异策略[15]. 该方法在产生局部解时,每个局部解变动选中解的一个决策变量. 极限优化策略的公式为 (11) (12) (13) βmax(xi)=max[xi-li,ui-xi],0 (14) 其中,xi为决策变量;h为0~1之间的随机数;q为正实数,称为形状参数,根据文献[15]将q设为11;βmax(xi)为当前决策变量xi可变动的最大值. 由于极限优化变异方法每次只改变一个决策变量,搜索范围较小. 因此对两个个体中的稀疏度较大的个体采用第2种变异策略[16],扩大搜索范围,该策略的计算公式如下.设当前稀疏解为x=(x1,x2,...,xn),n为决策变量个数,若种群总数为N,设置产生局部解个数为0.2N. (15) k=1,2,...,[0.2N] (16) (17) 为进一步验证NSGAII-URS的性能,选取NSGAII-DLS、GrEA[17]、MOEADD[18]、HypE[19]、RVEA[20]等5个典型的多目标优化算法进行对比实验. 其中NSGAII-DLS是一种基于密度的局部搜索NSGAII算法,GrEA引入网格排序、网格拥挤度和网格坐标距离等机制,以此来维持解的均匀性.MOEADD是一种基于支配和分解的进化多目标优化算法,HypE是一种用于多目标优化的超量估计算法,RVEA是一种用于多目标优化的参考矢量制导进化算法. 对于每个算法,都设置相同的种群规模和存档大小,重组、变异、采样等运算符都保持相同. 在同一个运行环境、相同参数设置下将不同的算法运行多次获得最终结果. 实验环境为Intel(R)Core(TM)i7-8550U CPU,内存8 GB,Windows 10操作系统,MatlabR2016b版本. 实验操作平台为通用的基于Matlab的多目标优化工具PlatEMO[21],版本v2.8. 由于双目标ZDT系列函数和三目标DTLZ系列函数被广泛地用于验证多目标优化算法,本实验分别采用 (ZDT1~ZDT4,ZDT6) 函数和(DTLZ4~DTLZ7) 函数来验证算法的性能.函数的特征、维度和种群规模如表1和表2所示. 表1 ZDT基准测试函数的特征、维度、种群模式 表2 DTLZ基准测试函数的特征、维度、种群模式 图3和图4分别是NSGAII-URS在ZDT系列和DTLZ系列函数上的优化效果图,可以看出对于凹、凸和非连续的多目标函数,该算法都能很好地逼近Pareto前端且分布比较均匀. 其中,对于ZDT系列的双目标问题和DTLZ系列中的真实Pareto连续问题取得了相对显著的优化效果,对于DTLZ系列中的多峰且非连续问题也达到了良好的快速收敛和均匀分布效果. 在实验对比部分,函数调用次数均为10 000次、指标结果分别是算法独立运行30次得到的平均值和标准差,表格中加粗部分为同一测试函数中获得的最优值. 在结果比较中,采用了Wilcoxon秩和检验比较算法性能差异性,置信度为95%,其中“+”、“-”、“=”分别表示显著优、显著劣、无差异于NSGAII-URS算法. (a) (b) (c) (d) (e) 为了比较不同算法性能,采用以下两个广泛使用的综合性能评价指标对算法进行验证. (1) 反世代距离(IGD).IGD通过度量真实Pareto前沿和算法所获得的Pareto前沿之间的接近程度来评价算法的收敛性和多样性,IGD的定义如下. (18) 表3是6个算法分别在ZDT系列测试函数上关于IGD指标的运行结果,可见 NSGAII-URS算法得到的IGD值的平均值和标准差均小于对比算法,且平均IGD值比对比算法的结果都要小1到2个数量级. 表4是在DTLZ系列测试函数上关于IGD指标的运行结果,可见本文算法在DTLZ6、DTLZ7上得到的IGD值是优异于其他5种算法的,在DTLZ4和DTLZ5上略差于NSGAII-DLS,但总体上还是比另外4种算法运行效果好. (a) DTLZ4优化效果 (b) DTLZ5优化效果 (c) DTLZ6优化效果 (d) DTLZ7优化效果 表3 ZDT系列测试函数上IGD的平均值和标准差 (2) 超体积(HV).HV衡量算法所获得的Pareto最优解集在目标空间所覆盖的范围大小,该指标可以同时衡量收敛性和多样性,计算公式如下. (19) 式中,PFt是t时刻算法所获得的Pareto前沿,是由参考点和个体形成的超体积. HV越大说明算法所得到的 Pareto前沿收敛性越好,分布越均匀. 表5是6个算法分别在ZDT系列测试函数上关于HV指标的运行结果,可见 NSGAII-URS算法在ZDT1~ZDT2、ZDT4、ZDT6上得到的HV值的平均值和标准差均小于对比算法,在ZDT3上略差于算法HypE,但相较于另外4种算法还是有明显优势的. 表6是在DTLZ系列测试函数上关于HV指标的运行结果,可见在DTLZ6~DTLZ7上本文算法得到的IGD值都是具有优势的,在DTLZ4上略差于算法MOEADD,在DTLZ5上略差于算法NSGAII-DLS,在后续的工作中可就这些问题进行更深入的研究. 由以上实验和分析可以得出,在实验指标设置相同的情况下,针对双目标和三目标优化问题,本文提出的NSGAII-URS算法可以获得更明显的优化效果. 表4 DTLZ系列测试函数上IGD的平均值和标准差 表5 ZDT系列测试函数上HV的平均值和标准差 表6 DTLZ系列测试函数上IGD的平均值和标准差 在多目标优化问题中,进化算法的环境选择上,在收敛性和均匀性中形成合理的平衡是一项艰巨的任务. NSGAII-URS算法在寻找最优解时,以NSGAII为搜索引擎,以领先解解集中的个体为基础进行局部搜索,为下一代优选解,增强了种群向Pareto最优前沿的选择压力.由于均匀性也是考核算法优越性的重要标准之一,本文提出在每次遗传过程中面向非支配解划分区域、定位失衡子空间,调整获得的Pareto前沿,使其在保持快速收敛的同时也具有良好分布性. 综合分析本文提出的算法与其他多目标算法在ZDT和DTLZ系列基准测试函数上的结果,显示NSGAII-URS在保持收敛和分布均匀之间的良好平衡方面是有效且具有竞争力的.3.3 区域失衡

4 实验仿真
4.1 实验环境和参数设置
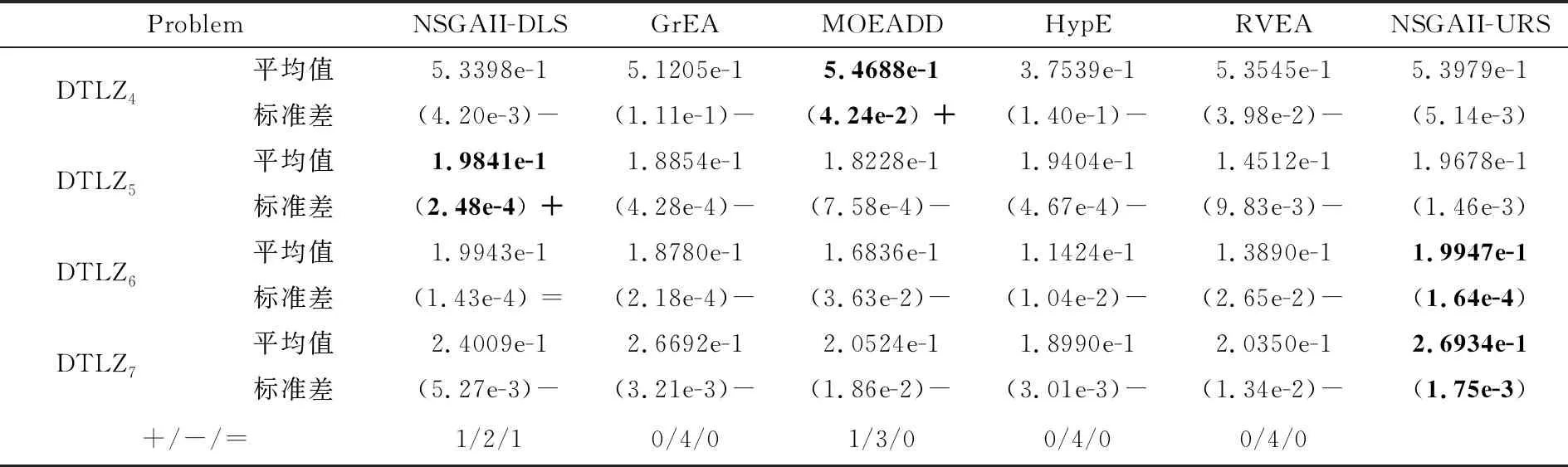
4.2 实验结果与分析