在位势对二维双原子正方晶格色散关系的影响研究

吕岿,杨建荣

(上饶师范学院 物理与电子信息学院,江西 上饶 334001)

晶格振动色散关系是联系微观结构和宏观性质的桥梁,确定了色散关系,原则上就确定了粒子的性质和系统的动力学行为及热力学行为,与实验结果互相验证,有助于理解晶体的宏观性质和微观机理,因此研究色散关系具有重要的理论和实际意义。对二维复式晶格振动色散关系的研究,人们已经做了很多工作[1-3],这些工作考虑了原子间的互作用势,但未涉及原子可能存在与邻近原子无关的在位势(on-site)的情形。研究表明,一定条件下,在位势可从根本上改变一维原子链声学支格波的性质[4-5],对二维单原子晶格的色散关系也有显著影响[6],对二维复式晶格色散关系的作用和影响如何,尚值得进一步探讨。本文以具有在位势的二维双原子正方晶格为例,建立和求解其晶格振动方程,讨论在位势对二维复式晶格色散关系及振动极化的影响特点。

1 振动方程组的建立和求解

设二维双原子晶格含有N个原胞,原胞中两个原子的质量分别为M1和M2,晶格周期为2a。将第l个原胞中的第n个原子在α(＝x,y)方向离开平衡位置的位移表示为uα(n,l),与第l＇个原胞中第m个原子之间的互作用力常数表示为,各原子的在位势力常数表示为η。在简谐近似下,具有在位势的二维双原子晶格振动的拉格朗日函数为:

将(1)式代入拉格朗日方程,可得到其晶格振动方程为:

在位势的存在不影响晶体的平移对称性,因此可设(2)式的解为:

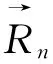
将(3)式代入(2)式可得:

其中Dαβ(m,n,)为含在位势动力学矩阵:

由(5)式可得久期方程为:

其中eα(m)、eβ(m)表示沿R m(l＇)-R n(l)方向的单位矢量在各坐标轴上的分量,γm表示第l个原胞中的第n个原子和第l＇个原胞中第m个原子之间的弹性耦合系数。显然,平移不变性要求各原子的互力之和为零:

将各原胞中质量为M1的原子均记为1,质量为M2的原子均记为2,并设M1、M2的最近邻弹性耦合系数为γ0,M1之间的次近邻弹性耦合系数为γ1,M2之间的次近邻弹性耦合系数为γ2。引入相对弹性耦合常数,相对在位势力常数,相对质量系数和特征频率(只考虑最近邻互作用时第一布里渊区中心的光学支最大频率[2])。由(5)(7)(8)式可得到具有在位势的二维正方晶格的动力学矩阵元素为:

将以上各动力学矩阵元素代入(4)式和(6)式,即可求得晶格振动的极化向量和振动频率。

2 色散关系及讨论

在研究晶格的振动色散关系时,选择波矢在第一布里渊区(如图1所示),即可得到全部振动特征。为简单起见,本文仅讨论两原子质量M1＝M2＝M即相对质量系数μ＝1时,二维正方晶格第一布里渊区沿ΓΧ、Γ-M 和X-M 三种对称方向的色散关系和极化情况。),可求得振动频率为:

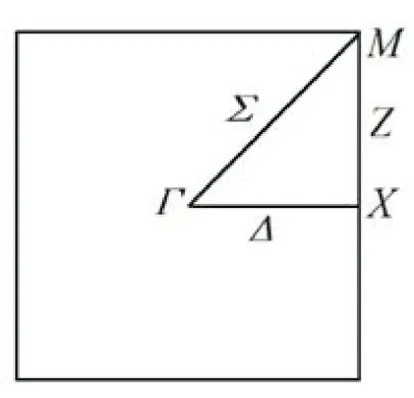
图1 二维双原子正方晶格的第一布里渊区

沿Δ≡(Γ-X) 方向(ky＝0,kx＝k∈),可求得振动频率为:

相应极化向量是一常矢,与互作用势和在位势无关:

只考虑最近邻互作用时(g＝0),相应极化向量为一常矢:

计入次近邻互作用(g≠0)时,相应极化向量亦为一常矢,但方向不同:

沿Z≡(X-M) 方向,可求得振动频率为:

只考虑最近邻互作用时(g＝0),相应极化向量为一常矢:

计入次近邻互作用(g≠0)时,相应极化向量不再为常矢,与原子间互作用γ0及γ有关,但仍与在位势无关:

以下分别取a＝1,g＝0或0．1,ψ＝0或0．3,得到只考虑最近邻互作用或同时考虑次近邻互作用时,沿Γ-Χ、Γ- M 和X- M 方向的色散关系分别如图2(a)、图2(b)所示。图中实线表示无在位势时的情况,虚线表示在位势存在时的情况。

从图2(a)、图2(b)可以看出,两种原子质量相同时,无论是否计入次近邻互作用,在位势η的存在均使Γ、X、M 各点及沿三种对称方向的声学支、光学支频率向上平移,平移幅度与特征频率有关,即与最近邻互作用耦合系数成正比,与原子质量成反比,但不改变这些对称点及对称方向上格波的简并度;布里渊区中心Γ点的频率不为零,出现了所谓频隙,这与在位势对一维原子链、二维单原子晶格色散关系的影响相同[4-6],是在位势影响色散关系的显著特征。需要指出的是,随着在位势的增大,两声学支的频率将逐渐上升,但即使接近或高于在位势为零时的低频光学支频率,因原子的极化向量不受在位势影响,声学支中两原子保持同向运动,故其声学模特征不变[7]。

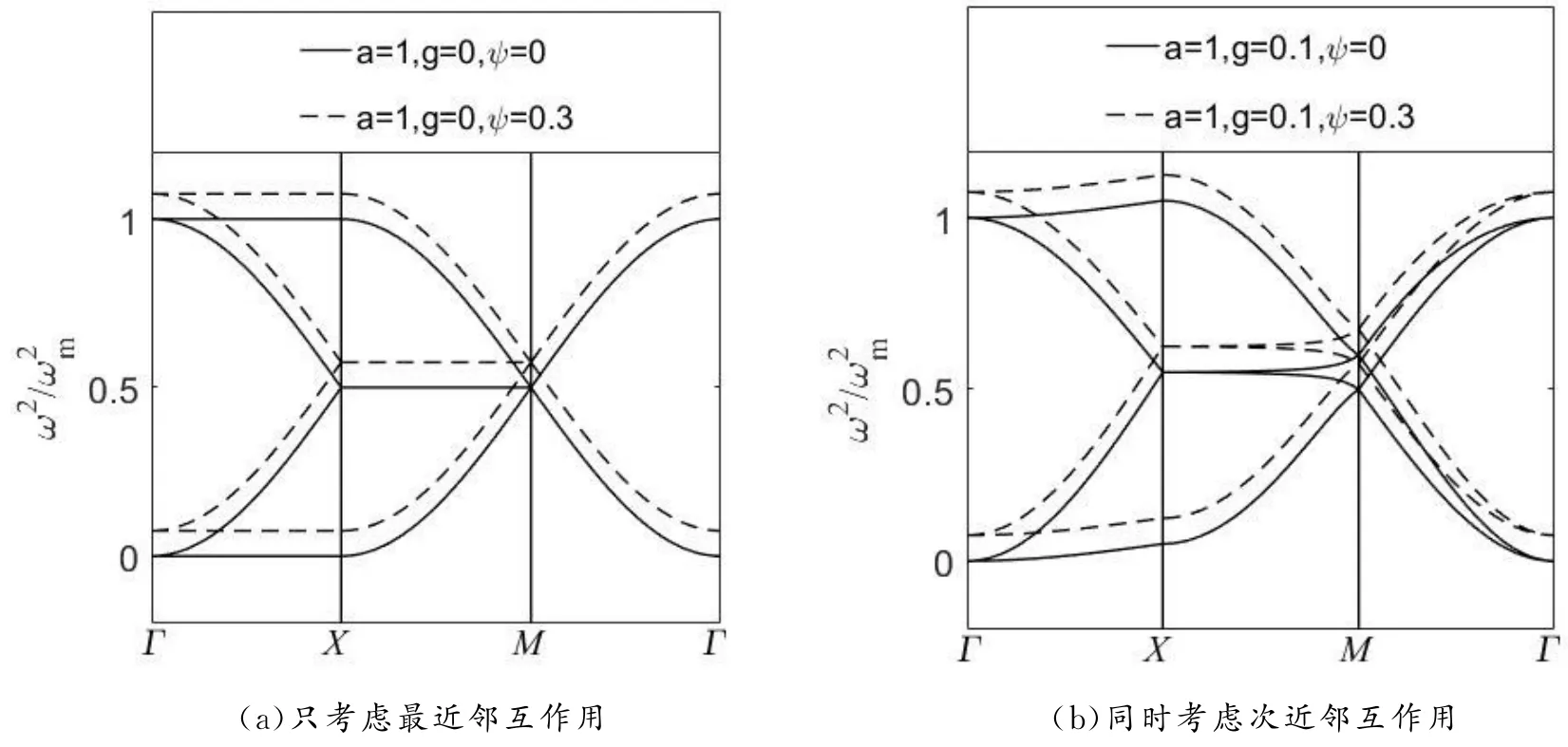
图2 具有在位势的双原子正方晶格的色散关系曲线

a、g、ψ取其他值时,情况与上述讨论类似,在此不再赘述。

3 结论

当原子存在与邻近原子无关的在位势时,若两种原子质量相同,二维双原子正方晶格第一布里渊区中Γ、X、M 各点及沿Γ-Χ、Γ- M 和X- M 方向的各格波频率均向上平移,平移幅度与原子质量成反比,与在位势和最近邻互作用成正比,与次近邻互作用无关;各格波的简并度及极化方向不受在位势影响;各低频支频率虽随在位势增大而上升,但保持声学模特征不变。当在位势为零时,本文的研究结果与文献[2]一致,表明我们使用的模型是正确可靠的。本文是对相关理论的一些基础知识的拓展[8],有望为固体材料微观机理的研究和相关的实验提供一定的理论参考和依据。