水下光场的迭代求解

何大华，李阳阳，周少杰

（华中光电技术研究所—武汉光电国家研究中心, 湖北 武汉 430223）

1 引 言

水下光电成像是利用可见光对水下目标进行成像的技术[1-12]，在国民经济乃至军事上有广泛的应用前景。由于水体对光线存在散射，无论是人工光源还是自然光源照射到水体时，都会在整个水域中形成水下光场[13-14]，其中处于目标和水下光电成像系统之间的水体散射将在成像系统靶面上形成背景干扰，降低目标对比度和成像质量。水下光电成像可分为主动和被动两种成像方式，水下主动光电成像利用系统自带的人工光源对水下目标进行照明，可以是卤素灯、LED灯或者蓝绿激光器等，水下被动光电成像利用自然光进行水下照明，包括太阳或者天空背景光等。可见光在水下传输时由于受到水体的强烈吸收和散射，其能量随距离增大按指数规律衰减，使得无论是被动还是主动方式，甚至近年来取得重要进展的水下激光成像技术[2-5]，其水下作用距离最多不过几十米。在另一个重要的水下应用领域，水下激光通信[15-16]中，水体的吸收和散射现象对通信距离和误码率同样会产生严重影响。

对水体散射等光学现象的研究可追溯到20世纪60年代，Duntley深入研究了光线被海水吸收和散射的基本性质[17]；GROSSO在理论建模和实验对比的基础上给出了体散射函数（VSF）与调制传递函数（MTF）的关系[18]；MERTENS给出水体点扩展函数（PSF）和光束扩展函数（BSF）的定义，并研究了二者与水体的固有光学参数（IOP）之间的关系[19]；JAFFE建立了水下成像的最优模型，发现调整光源和成像系统的相对位置能提升图像对比度[20]；HOU建立了简单的水下成像模型，并研究了PSF在自然水体中成像的有效性，利用PSF对图像进行去卷积复原，获得了较好效果[21-22]；VOSS给出了一个估算海水PSF的经验公式，可以用来预测任意长度水体的PSF[23]。国内方面，陈养渭对水下激光散射场进行了实验研究，并建立了散射椭球模型[24]；闫旭光利用Monte Carlo方法分析了激光前向散射的时间和空间特性[25]；宋庆君等研究了黄海、东海海区水体的后向散射系数与总悬浮物浓度的关系，为水色遥感提供了支撑[26]；李彩等对水体体散射函数的测量技术进展进行了综述[27]；许廷发等利用连续帧图像信息估算PSF，结合凸集投影法进行超分辨率成像重建[28]；褚金奎等引入偏振技术，提出了一种抑制水下图像后向散射的方法[29]。

本文以水体吸收和散射的基本过程为基础，在稳定光源照射以及体散射函数为球形对称的情况下，定量求解光线经水体多次散射后形成的水下光场分布。求解水下光场的过程阐明了水体对光线吸收和散射的微观机制，精确的水下光场数据为严格推导水体PSF和MTF提供了关键信息。

2 水下光场计算模型

2.1 基本概念

一般认为，准直窄光束在水下传输时能量衰减遵循朗伯-比尔定律[13]，即

其中P0为准直窄光束的初始功率，P为准直窄光束在水下传输距离r之后的功率，c为水体衰减系数，其倒数1/c称为衰减长度（Attenuation Length，AL），a为吸收系数，b为散射系数。

对于水下点光源，设光强为I0，则在水下传输距离r后未被吸收和散射的能量形成的径向照度为

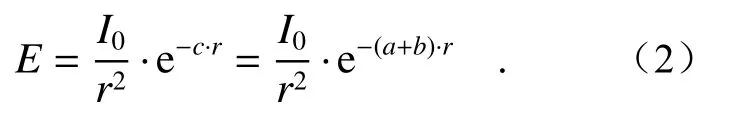
多次散射：光束或光子在水下传输过程中被水分子或水中杂质散射从而多次改变传输方向的现象。

球面照度：空间中某点的球面照度为全空间范围内入射到该点处一个小球内的光通量总和与该小球的表面积之比，可表示为4π立体角范围内对亮度的积分。球面照度也称为标量照度。

水下初始光场：在指定的水域中，光源发射的光能量进入水体传输过程中未被水体吸收和散射的部分在水下形成的球面照度分布。

水下散射光场：在指定的水域中，水体散射光形成的球面照度分布。

水下光场：在指定的水域中，水下初始光场与水下散射光场之和。

2.2 水下光场的形成过程

暂不考虑水气界面、水下物体等边界条件以及瞬态光源或光源功率波动的影响。假定在三维直角坐标系oxyz中充满了水体，衰减系数、吸收系数与散射系数分别为c、a和b，其中b=4πβ，式中 β为体散射函数[13]。下面以单点光源为例说明水下光场的形成过程，设在(x0,y0,z0)处有光强为I0的稳恒点光源S，则水下光场按如下步骤形成：

Ⅰ.点光源发出的光线经扩散和水体衰减后形成水下初始光场Et0。

Ⅱ.水下初始光场Et0使整个水域产生散射，形成一次水下散射光场Es1，叠加在Et0上形成一次水下光场Et1=Et0+Es1。

Ⅲ.一次水下光场Et1使整个水域产生散射，形成二次水下散射光场Es2，叠加在Et0上形成二次水下光场Et2=Et0+Es2。

Ⅳ.i次水下光场Eti使整个水域产生散射，形成i+1次水下散射光场Es(i+1)，叠加在Et0上形成i+1次水下光场Et(i+1)=Et0+Es(i+1)。

Ⅴ.以此类推，将形成水下初始光场Et0及水下光场序列Eti,i=1,2,3,······。

Ⅵ.Eti将收敛于水下光场Et。

根据以上思路，下面给出一般意义上的水下光场求解方程式。

如图1，点光源S发出的光在水下传输过程中会进行球面扩散，还会被水体吸收、散射，一部分光线继续沿原来的路径传播，在P点处形成的水下初始光场为

由于受到光源照射，水体也成为散射光源，M点处体积元dudvdw的散射会在P点处产生球面照度，对所有体积元散射产生的球面照度进行叠加可得到P点处的水下散射光场Es(x,y,z)。

图1 水下光场示意图Fig.1 Diagram of the underwater light field

设水下光场为Et(x,y,z)，则有

P点处的水下光场等于水下初始光场与水下散射光场之和，因而有

式（5）即为水下光场Et(x,y,z)的求解方程式，它属于第二类Fredholm积分方程，且未知函数有3个变量。在满足一定条件时，可利用行列式求解得到近似解析解[30]。本文从工程应用出发，给出该类方程的数值迭代解法，具体计算方法在3.1节中给出，仅考虑水下光场含一个变量的情形，对多个变量的情形可依此类推。

3 典型水下光场的计算方法

3.1 太阳照射下水下光场的计算方法

2.2节给出了理想情况下水下光场的计算方法，实际中总会存在一些边界条件，下面给出太阳照射下足够大平静水面下的水下光场。

仅考虑太阳照度，忽略天空背景亮度的影响，太阳光以一定角度平行入射进入水中，并发生反射和折射。折射光线经吸收和散射后，剩下部分继续向前传播，随深度增加能量越来越小。散射光线同样会被吸收、散射或者继续传播，在水下形成多次散射，进而形成稳定的水下光场。

如图2所示，从对称性考虑，太阳照射下的水下光场的数值仅仅与深度有关，而与水平坐标无关，因此，水下光场函数可用深度h为自变量的一元函数Et(h)表示。

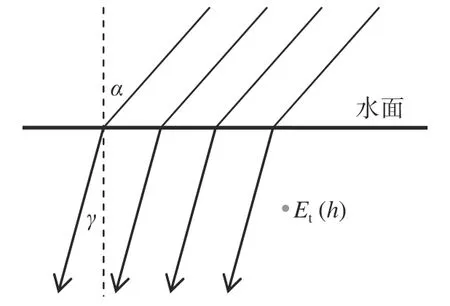
图2 太阳照射下的水下光场Fig.2 Underwater light field from the sun

设太阳光的入射角为α，水体的折射率为nw，由折射定律可求出折射角γ，再由Fresnel公式[31]可求出入水时的反射率Rα和透射率Tα。

设与入射太阳光垂直方向上的照度为Esun，则水下深度h处的水下初始光场为

以图3来说明水下深度h处P点的水下光场Et(h)的形成过程，Et(h)=Ed(h)+Es(h)，Ed(h)为水下初始光场，表达式为式（6），Es(h)为水下散射光场，在数值上等于水下所有微体积元散射在P点形成的球面照度之和。为此，建立直角坐标系，以P点正上方与水面相交点O为坐标原点，水平向右为x轴正向，垂直于纸面向外为y轴正向，竖直向下为z轴正向，则P点的坐标为P(0,0,h)。

图3 水下球面照度形成原理Fig.3 Formation of underwater spherical illuminance

PO与深度为z的水平面相交于C，以C为圆心在水平面内画半径为r的圆C，MN为直径，其中M与M'、N与N'分别关于水面对称，PM'交水面于A点，PN'交水面于B点，以M'N'为直径的水平圆的圆心为D，由图3可知，在xOy平面内，以MN为直径的圆周上所有点到P点距离相等，记为。

圆C上的微体积元dV=2πr·drdz，体积元dV在P点形成的球面照度dEs1为

还应考虑圆C上的微体积元散射光经水面下表面反射后对P点形成的球面照度。M点发出的光线经A点反射可到达P，可等效为从M'发出的光线直接到达P。同理，N点发出的光线经B点反射也可到达P，可等效为从N'发出的光线直接到达P，故这组反射光线可等效从圆D发出，并经过了长度为PM'的水程到达P点，记为。

注意到光线MA在A点反射时有能量损失，由入射角α根据Fresnel公式可计算出反射率Rα。由此可知圆C上的微体积元经水面下表面反射在P点形成的球面照度dEs2为

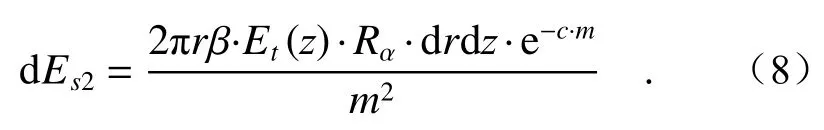
综合以上结果，圆C上的微体积元在P点形成的球面照度dEs为

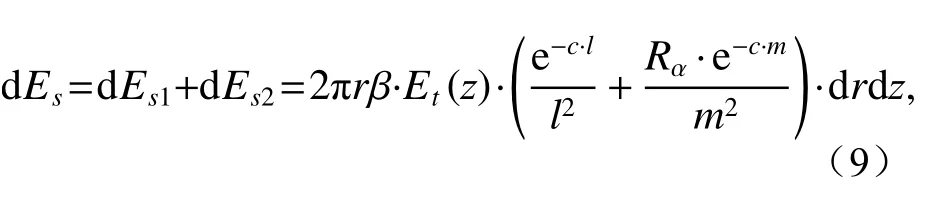
其中Rα、l、m均为h、r和z的函数。

由此可知P点的水下散射光场Es(h)为

故水下光场Et(h)为

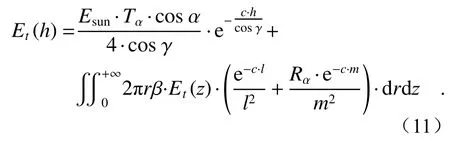
式（11）为第二类Fredholm积分方程，对式(11)进行代换简化得到

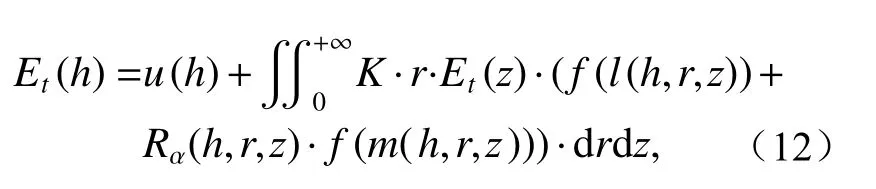
其中令深度h及积分变量r和z的细分间隔均为Δ，并对式（12）进行数值化得

其中，k=1,2,3,······。

由于水体对光线的衰减严重，水体散射对距离超过10AL的区域影响可以忽略，因此在计算时，可适当限定计算范围，基本不影响计算精度，例如计算10AL深度内的水下光场时，可令k=1,2,3,···,N，并满足NΔ＞20AL。据此，将式（14）改为以下迭代形式

式（15）的迭代求解流程图如图4所示。

图4 水下光场迭代求解流程图Fig.4 Iterative solution flow chart of the underwater light field

迭代6次后Et(kΔ)已基本收敛，可输出结果。下面利用Matlab仿真程序迭代计算太阳照射下的水下光场，选取晴朗天气、洁净海水条件下的水下光场进行计算，可以从仿真曲线直观看出这一典型条件下的水下光场随深度的变化情况。

仿真程序的相关参数取值如下：太阳光照度：Esun=105lx；太阳光入射角：α=45°；水体折射率：nw=1.33；衰减系数：c=0.1/m；吸收系数：a=0.05/m；散射系数：b=0.05/m；体散射函数：β=1/80π/(m·sr)；Et(h)深度精度：Δ=0.2m；

Δ取值的依据是，当Δ=0.02 AL时，水下光场精度足够，此例中AL=10m，因而Δ=0.2m。

图5是水深100 m（10AL ）以内仿真程序输出的水下光场迭代曲线。

图5 太阳照射下水下光场迭代曲线Fig.5 Iteration curves of the underwater light field from the sun

由于Et(h)=Ed(h)+Es(h)，为了直观表达，不直接显示Et(h)，而显示分量Ed(h)和Es(h)，其中Ed(h)是定值，在i从0到5这6次迭代过程中保持不变，而Es(h)在迭代过程中逐渐收敛。图6最上面的曲线为Ed(h)，下面6条曲线为Es(h)的6次迭代变化（包括Es(h)=0），顺序为从下至上，从图6中可以看出6次迭代后已基本收敛。

3.2 均匀亮度天空背景下的水下初始光场

由3.1节对水下光场的求解过程可知，当光源选定为均匀亮度天空背景时，计算过程中唯一差别是求解水下初始光场Ed(h)，在不同的光源照射下，只要求出了Ed(h)，则可利用上述方法得到迭代方程式对水下光场Et(h)进行求解。下面推导均匀亮度天空背景下的Ed(h)表达式，并给出Matlab程序的仿真结果。

由于天空背景为大型面光源，各部分光线入水时的入射角 α各不相同，因此，求解Ed(h)时需对上半球天空背景进行积分。

如图6所示，天顶角为α的微球带对应的立体角为dΩ=2πsinαdα。

图6 天空背景在水面形成照度Fig.6 Illuminance on the surface with the sky as the background

设均匀天空的亮度为Lsky，对水下初始光场求解时，可将微球带发出的光线等效为入射角为α的一组平行光，而且垂直于入射方向上的照度为dE=2Lskyπsinαdα，则可得均匀亮度天空背景下水下初始光场为

编写Matlab仿真程序计算Et(h)，假设天空亮度为Lsky=5000cd/m2，水体光学参数及Et(h)的深度精度同3.1节，则Et(h)在深度10AL之内的迭代曲线如图7所示。其中各曲线的意义与图5相同。

图7 天空背景照射下水下光场迭代曲线Fig.7 Iteration curves of the underwater light field with the sky as the background

3.3 点光源形成的水下初始光场

3.3.1 点光源在水面以下

设水深h0处有均匀发光点光源S，光强为I0，水体衰减系数、吸收系数及散射系数同上，计算水面平静时光源S形成的水下初始光场。

如图8所示，由于对称性，仅分析通过S点的一个竖直平面内的情形，对于水下任意点P，设其深度为h，离S点的水平距离为x，则P点处的水下初始光场记为Ed(h,x)。

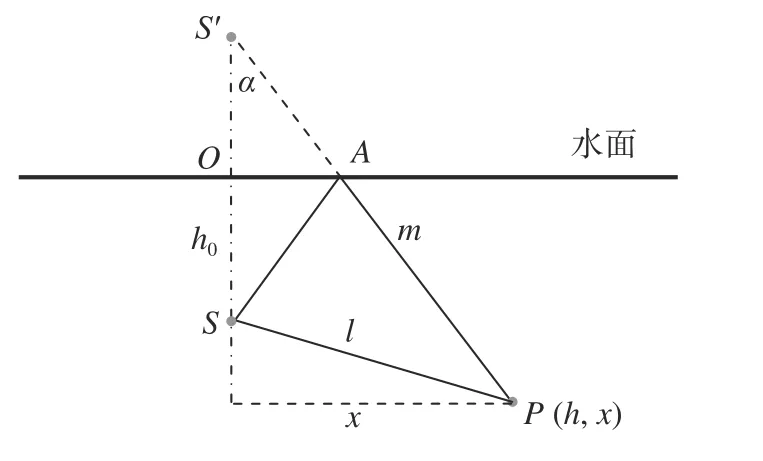
图8 水下点光源形成的水下初始光场Fig.8 Underwater initial light field by an underwater point light source

光源S直射到P点处的球面照度为Ed1(h,x)，光源S点发出的光线经水面下表面反射后照射到P点处的球面照度为Ed2(h,x)，则

S点发出的光线经水面下表面反射的光线可以等效为S点关于水面的对称点S′点发出，经过了水程S′P的衰减以及反射率Rα的修正，则

3.3.2 点光源在水面以上

设水面以上高h0处有均匀发光点光源S，光强为I0，水体衰减系数、吸收系数及散射系数同上，下面计算水面平静时光源S形成的水下初始光场。

如图9所示，通过S作竖直线与水面交于O点，显然，水下初始光场关于直线SO旋转对称，因此只分析通过S点的竖直平面内的情形。对于水下任意点P，设其深度为h，离O点的水平距离为x，则P点处的水下初始光场值记为Ed(h,x)。SO与深度为h的水平面交于M，则以M为圆心，x为半径的水平圆上的水下初始光场值均为Ed(h,x)。

光源S发出的光线中入射角为 α的光线形成一个锥角为2α的圆锥面，其水面入射点集合是圆，圆心为O，直径为AB，设折射角为γ，透射率为Tα。

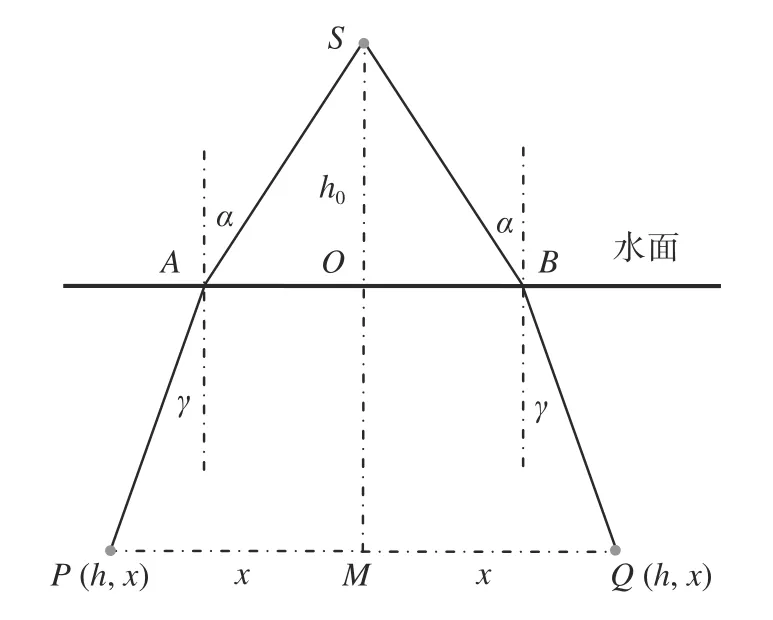
图9 水上点光源形成的水下初始光场Fig.9 Underwater initial light field by an overwater point light source

锥角为2α的圆锥立体角为2π(1-cosα)，考虑圆锥2(α+dα)与2α之间的光线折射入水能量传输情况，其入射角均为α，透射率均为Tα，立体角为2πsinα·dα，对应能量为Φ0=2πI0sinα·dα，该能量经水面反射和水体衰减后到达深度h处时变为

由图9可知x=h0·tanα+h·tanγ，在深度h处，折射光线是一个圆环，内半径为x，外半径为x+dx，其面积ds=2πx·dx。由于P处的球面照度为Ed(h,x)，则Φh又可表示为

比较式（20）和式（21）并化简得

3.4 小结

以上3小节分别给出了平行光、天球光、水下和水上点光源形成的水下光场的计算方法，并考虑到水面下表面反射的影响。假定光线的传输及散射现象具有独立性和叠加性，则在以上各类光源的任意组合下求解水下光场也是可行的。在复色光入射的情况下，也可以对各个波段分别计算然后进行积分得到结果。这些光源的选取具有一定的代表性，因此，利用该计算模型可解决一般意义上的水下光场分布问题。

在自带光源的主动水下光电成像应用中，为了提高功率密度和减小后向散射，光源的照明区域往往局限在有限的角度范围内，这时水下光场也可以通过上述方法求解，因此该计算模型可扩展应用到边界条件更为复杂一些的情形。

已知水下光场分布，则易求得水体的表观光学参数[13]，因此，该计算模型还可直接用于求解水体的表观光学参数（AOP）。

4 结 论

水下光电成像技术目前得到了广泛的关注，在未来具有可观的经济和军事价值。近年来军事方面的一个紧迫需求是水下对空跨介质成像[32]，由此水下航行器得以在安全深度下对空中威胁目标进行预警。其主要难点在于：一是海面波浪引起的图像碎化问题[33-34]；二是水体对光线的吸收和散射效应引起的图像模糊。这需要研究水下光场分布，改善图像质量，以提升水下航行器的预警深度。

从基本的吸收和散射模型出发，考虑到有无边界条件，从理论上严格推导了几种典型光源照射下的水下光场分布，这对于分析水体PSF以及MTF具有重要意义，也为研究水下光电图像的退化模型奠定了基础。虽然只给出了水体VSF为球形对称且水面平静情形下水下光场的求解方法，但对于VSF具有任意形式、水面波形具有一阶连续可导的情形也能求解，这为一般意义上水下光场问题的定量求解提供了借鉴。

然而，在实际问题中，光源特性并不稳定，水体散射特性在空间上也不均匀，且存在湍流时变扰动[35-37]，故水下光场是动态变化的，且水下各种噪声也对计算结果有较大影响。因此，在具体的水下光场求解过程中，需要结合估计、现场测量、大数据处理等经验方法进行分析，而将本文的方法作为必要的参考。