液压闸门增力式举升机构优化及有限元分析

李凯旋，耿晔晗，窦立玮，王 湛，闫永生

（中国水利水电科学研究院，北京 100048）

1 研究背景

目前，常见的液压闸门主要包括合页活动闸、液压升降坝、钢坝闸等[1]，但多采用直推式举升机构，该类闸门在建拦蓄高度多为1～5 m，目前，最高在建也仅为6 m，资料可查建于南洋河天镇县[2]和辽宁省海城市[3]。随着水利工程的发展，闸门也不仅仅局限于常规功能，需求也逐渐向景观性、生态性、控制性等多重功能方向发展[4-6]，闸门拦蓄高度从1～6 m的常规拦蓄高度逐渐向6～8 m的较高拦蓄高度发展，举升机构已不能完全满足当前水工闸门的需求，亟待解决寻找一种适合于4～8m较高拦蓄高度尤其是拦蓄高度大于6m的举升机构，促进液压闸门技术的发展与应用。

目前，对于闸门的工作特性已有一些研究基础。如谢良平[7]建立常见3 m、4 m、5 m坝高的直推式液压升降坝物理模型试验，研究分析其在不同开启方式下，正常泄水及挡水的泄流特性分析。陈业银等[8]介绍了直推式液压升降坝的结构、原理及特点，并采用弹性力学三维有限元法计算不同工况下面板及支承结构的应力和变形；周建方等[9]提出了钢闸门结构正常使用极限状态可靠度分析的3种计算模式，对钢闸门结构在设计规范正常使用极限状态可靠指标进行了校准计算和分析。

但是对于非直推式举升机构的工作特性研究相对来说几近空白，仅有刘明军等[10]介绍了一种非直推式新型液压拦河坝的优缺点，该种结构推力液压缸行程较直推式的短，且每个支撑点都是三角形支撑，稳定性更高，但也仅仅适用于6 m闸以下。俞昊捷等[11]介绍了一种非直推式折叠液压坝支撑结构在升降过程中的工作特性及有限元分析，并分析了该结构在不同面板闭合角度下应力的变化规律及坝前泥沙淤积对该种结构的影响。

而本文的增力式举升机构是在直推式举升机构的基础上进行发展的新型机构，该举升机构在升降过程中，受力不断发生变化，举升机构的强度和稳定性都需要进行深入分析及计算。本文结合其运动原理计算其在较高拦蓄高度4～8 m情况下，液压缸缸径、行程、稳定安全系数随启闭角度的变化规律及关系，确定其在运行时的工作状态情况，通过分析其安全稳定性，判断其适用的拦蓄高度工况条件。并以6 m宽、4 m高增力式举升机构为模型案例，建立三维有限元模型，开展静力学仿真分析计算，模拟超高溢流30 cm工况下的各关键结构应力、应变及变形情况，提出需要改进的部件及改进措施，为液压闸门增力式举升机构在较高拦蓄高度下的设计、改进和应用提供理论依据。

2 结构模型建立及计算

2.1 三维模型及计算参数建立首先建立液压闸门直推式、增力式举升机构三维可视化实体模型，能够保证这两种举升机构的正常运行，且都可以实现闸门启闭角度0°～75°任意角度挡水及泄水。直推式举升机构包括液压缸、底铰支座、铰轴等。由液压缸旋转伸缩直推门叶，门叶绕底轴旋转，实现升闸挡水，降闸泄水功能。直推式举升机构结构简单，液压缸小角度直推和支撑，不仅安全可靠，也具有一定景观性[12-13]；增力式举升机构包括门叶、上折叠杆组合、下折叠杆组合、底轴铰链总成、综合支架等。其中，上折叠杆与下折叠杆和液压缸连接于连接轴，在连接轴处发生折叠，液压缸伸缩旋转推动连接轴，上下折叠杆发生旋转转动，推动门叶绕底轴旋转，升闸挡水、降闸泄水。该举升机构与直推式相比，缩短了液压缸的行程，也节省了折叠连杆下放后的空间[14]。具体液压举升机构三维结构见图1，计算结构见图2，计算参数见表1。

图1 举升机构三维详图

图2 举升机构计算结构

表1 举升机构参数 （单位：mm）

2.2 计算公式模拟工程条件，当闸门倒伏时，坝面水平，即启闭角度为0°；当闸门立闸时，门叶有一定角度倾立，即启闭角度为75°。工况为闸前超高溢流30 cm，闸后无水，参考文献[15]，启闭角度为0°、15°、30°时，按动水压力计算；当启闭角度大于40°、60°、75°时，按静水压力计算。

对于直推式结构，将门叶OO′与液压缸AB看作平衡力系，建立对O点弯矩为0的静力平衡方程，推导出液压缸受力，即：

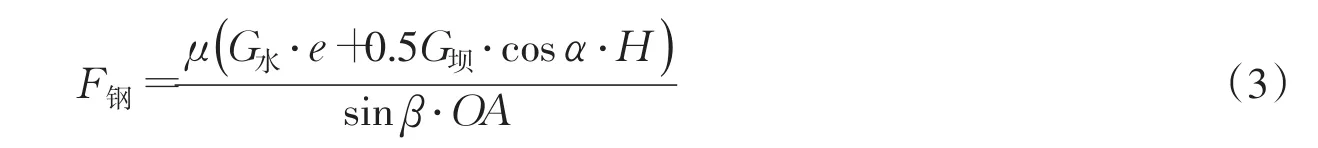
对于增力式结构，首先将门叶OO′、上折叠杆AB作为一平衡力系，该力系中考虑闸门所受水压力，闸门自重，建立对O点弯矩为0的静力平衡方程，得到上折叠杆所有推力；然后将上折叠杆AB、下折叠杆BD、液压缸CE整体作为一平衡力系，该力系中考虑上折叠杆，液压缸，下折叠杆受力，建立对D点弯矩为0的静力平衡方程，推导出液压缸受力公式，即：

液压缸的液压杆直径采用公式

液压缸稳定安全系数根据文献[16]计算。式中：G水为坝面所受水压力；G坝为坝重；e为水压力中心离底部距离；μ为安全系数，取1.2；b为单支液压缸所承受坝面长度，取3 m；H为坝面长度；h为拦蓄高度；γ为水的容重，取10 kN/m3；g为重力加速度，取10 m/s2；h1为超高溢流，取30 cm；h2为坝面底点距水面的垂直距离；α为启闭角度；β为液压缸与坝面夹角；OA为坝面底轴距上折叠杆与门叶交点的距离；P为工作压力。

液压缸稳定安全计算，采用欧拉公式[17]计算：

式中：k为液压缸稳定安全系数；Fcr为液压缸受压临界压力；F为液压缸所受轴向压力；E为活塞杆材料纵向弹性模量，取2.06×105MPa；Id为活塞杆的截面惯性矩；μ0为长度折减系数；μ为长度系数，两端铰接μ=1；Lz为活塞杆全行程外伸状态支点间距。

2.3 液压缸缸径随启闭角度的变化规律如图3所示，两种举升机构在闸门开启过程中，缸径随着启闭角度的变化有很大的差别。直推式举升机构，起推时即启闭角度为0°时候液压缸受力大，随着闸门的起升，液压缸受力逐渐减小，减小到闸门升起启闭角度45°左右，液压缸受力逐渐增大至完全升起即启闭角度为75°时停止，当闸门完全升起时，液压缸受力接近起推时的受力情况，由此可以看出，直推式举升机构在起推时，液压缸受力最大，启闭角度为75°时，受力与起推时接近，相对来说也比较大。而增力式举升机构，起推时，液压缸受力很小，随着启闭角度的增加，受力逐渐增大，增大到启闭角度30°时，达到最大，然后液压缸受力逐渐减小，直到闸门完全升起，液压缸受力最小，由此可以看出，该结构在起推时和完全升起时，液压缸受力最小，可以有效减小液压缸的损坏，增长闸门的使用寿命。

图3 液压缸缸径随启闭角度的变化规律

2.4 液压缸缸径及行程随拦蓄高度的变化规律通过2.3节确定最大允许缸径值，选取液压缸参数，揭示液压缸缸径及行程随拦蓄高度的变化规律。如图4所示，两种举升机构的液压缸缸径和行程都随着拦蓄高度的增加而增大，并存在一定线性关系，直推式举升机构的缸径随着拦蓄高度的增加递增最慢，增力式举升机构的液压缸缸径随着拦蓄高度的增加递增最快，说明在同等较高拦蓄高度情况下，直推式的缸径较小，且随着拦蓄高度的增加，缸径增速较慢，存在一定的优势。相反，直推式举升机构的液压缸行程随着拦蓄高度的增加递增最快，增力式举升机构的液压缸缸径随着拦蓄高度的增加递增最慢，说明在同等较高拦蓄高度情况下，增力式举升机构中液压缸行程较小，且随着拦蓄高度的增加，行程增长较慢，存在一定的优势。

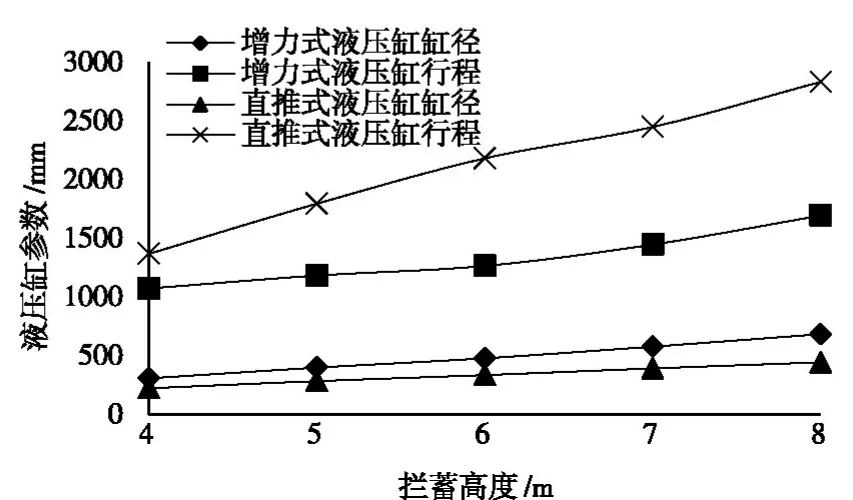
图4 液压缸缸径及行程随拦蓄高度的变化规律

2.5 液压缸稳定安全性随拦蓄高度的变化规律闸门在升降过程中，液压缸整体承受轴向压力，且活塞杆全行程外伸状态支点间距Lz与液压杆杆径d之比大于10，可能就存在风险，需要进行安全稳定性计算。直推式举升机构中细长比在13～14范围内，已经超过10，安全稳定性较差，需要进行安全稳定性的校核计算，而增力式的细长比在5～6范围内，安全稳定性较高。液压缸所受轴向压力F与临界力Fcr比为液压缸的稳定安全系数，且该系数不应小于3.5[16]。由图5可知，随着拦蓄高度增加，该系数变化存在一定的趋势。增力式举升机构的稳定安全系数随着拦蓄高度的增加而增大，非常安全稳定。但是直推式举升机构的稳定安全系数随着拦蓄高度的增加而减少，且在拦蓄高度大于6 m时，该系数已基本小于3.5，存在一定安全隐患。由此可知，增力式举升机构适合于4～6 m较高拦蓄高度，尤其适合于拦蓄高度大于6 m的情况下，直推式举升机构已经不能应用于拦蓄高度大于6 m的钢构闸门。

图5 液压缸稳定安全性随拦蓄高度的变化规律

3 有限元分析计算

采用有限元方法对增力式举升机构开展静力学仿真分析计算，以模拟设定工况下结构受力及变形情况。结构整体单元采用solid186实体单元，边界条件设置按项目实际情况简化设置，闸体模型宽度6000 mm，高度4000 mm，坝面可在0°～75°间转动，选取计算角度为（0°、30°、45°、60°、75°），闸体主体材料采用Q235B钢，其他材料如轴、套等转动部件为45#钢，闸体厚度为10mm，预埋件厚度为20 mm，底部钢板通过地锚螺栓与基础锁紧固定，坝底基础为钢筋混凝土，施加荷载为拟承受坝顶溢流300 mm时，闸门承受静水压力载荷模拟计算，各部件旋转部位设置为No Separation（不分离接触），滑移部位（液压缸）设置为bonded（绑定接触）。网格划分采用自动网格划分，设置整体网格划分最大尺寸100 mm，上折叠杆、下折叠杆、底轴铰链总成及综合支架细化网格，最大网格尺寸设置为20 mm，模型总节点数量为1 029 677个，网格数量为541 915个。

在农村地区，这种情况可以逆转。在自然状态下的木材存活和生长时释放VOCs;林地和森林中的空气可以比许多室内环境具有更高的浓度。

三维有限元网格划分模型如图6所示，具体分析主要部件的应力、应变及整体位移情况，主要部件包括闸门整体、门叶、底轴铰链总成、综合支架、上折叠杆组合、下折叠杆组合及铰链轴、套等，计算所用材料特性详见表2。

图6 三维有限元网格划分模型

表2 材料特性

3.1 各部件应力最大值随启闭角度的变化规律主要部件的应力最大值随闸门启闭角度的变化详见图7，可知：（1）门叶所受应力随着启闭角度的增大而增大，并且在60°～75°的过程有明显增大趋势；（2）除门叶以外的其他主要部件受应力情况与闸门整体受力趋势一样，随着启闭角度的增大而增大，但是在60°～75°的过程却逐渐减小；（3）以材料屈服强度为判断依据，分析该举升机构在不同启闭角度下超过材料屈服强度的情况。对闸门整体进行应力计算，可知在60°情况下，位于该举升机构关键部位即上折叠杆与下折叠杆的连接轴位置所受应力最大，高达358.2 MPa，如图8（a）；在75°情况下，门叶所受最大应力高达336.54 MPa，位置处于门叶底轴液压缸驱动连接处，如图8（b）；（4）在30°～60°情况下，底轴铰链总成中底轴铰链座立板位置高达330.83 MPa，如图8（c）；综合支架立板高达265.12 MPa，如图8（d）；上折叠杆组合中上折叠杆结构板高达358.2 MPa，如图8（e）；下折叠杆结构板所受应力较小，仅为156.04 MPa没有超过屈服强度，如图8（f）。

图7 各部件应力最大值随启闭角度的变化规律

图8 应力超过屈服强度应力云图

3.2 各部件应变最大值随启闭角度的变化规律主要关键部位的应变最大值随闸门启闭角度的变化详见图9，可知：闸门整体及门叶等效应变随着启闭角度的增大而增大，并且在60°～75°的过程有明显增大趋势；除闸门整体及门叶以外的其他主要部件等效应变情况随着启闭角度的增大而增大，但是在60°～75°的过程逐渐减小；在75°情况下，闸门整体及门叶应变的值最大，为2.66×10-3mm/mm。

图9 各部件等效应变最大值随启闭角度的变化规律曲线图

3.3 闸门整体随启闭角度的变形情况由图10可知：闸门整体变形最大值在随着启闭角度的增大先增大后减小，如图10（a）；启闭角度为30°时，变形量最大，达到26.511 mm；选取启闭角度为30°的三维云图为例说明，闸门主要变形的位置位于门叶前端，需要加强该处强度，如图 10（b）。

图10 整体变形随启闭角度的变化情况

4 结论

（1）液压闸门增力式举升机构能够实现闸门启闭角度0°～75°任意角度挡水及泄水，当闸门开启0°～30°时，增力式举升机构的液压缸受力逐渐增大，而后在30°～75°，受力逐渐减小，尤其当立闸挡水（即开启角度为75°）时，液压缸受力最小，这在一定程度上，可以大大减少液压缸的损耗，延长闸门的使用寿命。

（2）随着闸门拦蓄高度的增大，增力式举升机构与传统直推式举升机构相比稳定性更强。传统直推式举升机构随着拦蓄高度的增加，液压缸安全稳定性越来越差，更适用于拦蓄高度小于6 m的工况条件；而增力式举升机构随着拦蓄高度的增加，液压缸安全稳定性越来越好，说明增力式举升机构更适用于较高拦蓄高度4～8m的工况条件。

（3）除在垂直作用于闸面的集中载荷作用下施力区域出现高应力外，增力式举升机构在各工况下应力水平均不超过材料抗拉强度，局部应力集中处应力水平小幅超过了材料屈服强度；在垂直作用于闸面的集中载荷作用下，施力区域出现高应力，建议要尽可能加大作用面面积，分散集中载荷，提高闸门的稳定性；底轴铰链总成、铰链轴套区域及综合支架存在应力集中，建议加强焊接质量检测，防止疲劳开裂等失效；增力式举升机构关键部件即上折叠杆与下折叠杆的连接轴部位、上折叠杆结构板结构突变处所受应力最大，高达358.2 MPa，小幅度超过了材料屈服强度，建议增加连接轴轴径、结构板厚度或者增加过渡圆弧等结构消除应力集中，保证关键部件安全。

（4）闸门整体及门叶应变最大值随闸门启闭角度的增大而增大，其他主要部件等效应变情况随着启闭角度在0°～60°时增大而增大，在60°～75°的过程逐渐减小，75°时闸门整体及门叶应变的值最大，为2.66×10-3mm/mm。

（5）闸门整体变形最大值在随着启闭角度的增大先增大后减小，在启闭角度为30°时，变形量最大，达到26.511 mm，主要变形的位置位于门叶前端，建议加强该处门板厚度或添加增强构件等，减少门叶变形量。