基于MIF的正弦调谐模态试验频率误差分析与仿真
祝明昊 孔凡平
(北京强度环境研究所,北京 100076)
0 引言
结构的模态参数是表征结构动力学特性的关键。在航天领域,飞行器结构的模态参数至关重要,是建立、修改和优化动力学模型,动强度设计,以及控制系统稳定型设计的重要参数。对于大型航天运载器,如运载火箭、导弹武器等,主要采用多点稳态正弦调谐模态试验来辨识模态参数。
多点稳态正弦调谐模态试验,美国称为地面振动试验(GVT),欧洲称为地面共振试验,其精度高,误差小,已经成为大型复杂航空航天结构模态试验的常用方法之一,美国的Ares I-X运载火箭[1]、Galileo号木星探测器[2]等航天器的模态试验均采用了此方法。二十世纪,Kennedy和Pancu首先阐明了振动响应向量的实虚部概念并应用于振动试验,模态物理分离技术初步发展。R.C.Lewis和D.I.Wrisley提出了用多点激振的相位一致性判别进行模态分离,建立了多点稳态正弦调谐模态试验的基础[3],在选定的模态频率下,通过调节激振力来补偿结构的阻尼力,集中正弦激振的能量激出单一的模态,使结构在多个激振器同时激励下达到相位共振状态,得到结构的无阻尼纯模态[4]。目前主要的调节激振力的方法可分为经典调力法、最佳力分布计算法和指示函数法三大类。指示函数法发展迅速,此方法依据相位共振原理,将结构总体响应的某一函数作为目标函数来指导调节激振力[5]。模态参数辨识方法主要有导纳圆拟合法、复功率法、半功率法和对数衰减法等。
在调谐试验中,由于实际结构无法完全达到相位共振,导致模态纯度不够,实测的模态参数存在一定的误差。针对模态纯度的表示方法,法国曾在多点激振系统中采用总体相位角的方法[6],对每一测点响应的相位角进行总体加权,以此来表示模态纯度;西德的宇航模态试验中采用模态指示函数(MIF),以测点响应的实部加权求和与幅值之比最小的原理来描述模态纯度;美国航天飞机的地面垂直振动试验中采用了模态纯度比(MAP)的概念[7]。在我国的航天行业标准中[8],规定了以MIF作为参考的误差评估标准(认为MIF值大于0.9为纯共振,0.7~0.9为共振较好,小于0.7为共振较差),相位散布图法(加速度、位移、应变测点落在虚轴上,速度测点落在实轴上),以及在同样试验条件下进行重复试验,对试验获得的模态参数的一致性进行评定。但在目前的研究中尚未找到对实测模态参数具体误差值的量化评估方法。
1 频率误差分析的理论基础
1.1 多点稳态正弦调谐模态试验
辨识火箭/导弹的模态参数需要进行全箭/弹模态试验[9],主要采用多点稳态正弦调谐模态试验。试验一般在全箭振动塔内进行,采用弹簧绳悬吊的支撑方式模拟自由边界,要求支撑系统的固有频率尽可能小于被测结构的第一阶模态频率。试验中多台激振器同时激振,并根据激振器的位置控制激振力的相位为同相或反相,控制激振频率在特定的某阶模态频率附近,小幅度调节激振频率,尽可能达到相位共振状态。试验中当MIF值达到极大值时,此时的激振频率即认为是该阶模态频率。
对于弹性阻尼n自由度系统,其运动微分方程为
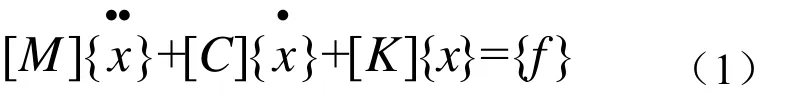
因此,向量{x}可以表示为代入式(1)可得
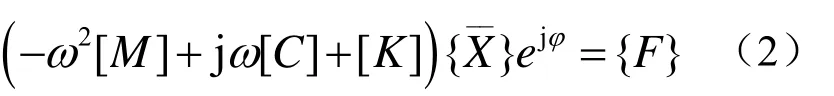
由实部虚部分别相等,可得
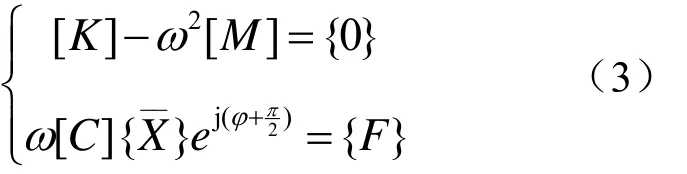
满足 [K] -ω2[M]= {0}的ωr为第r阶模态频率值,代入可得第r阶模态振型为{φr} ,进而得到满足第r阶模态相位共振条件的激振力为
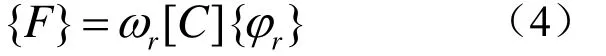
试验中通常用模态指示函数(MIF)作为所激励模态纯度的参考
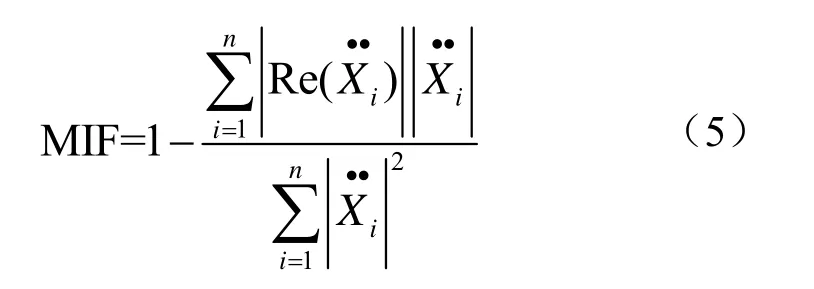
MIF值是由加速度响应的幅值和相位决定的。当某测点加速度响应超前参考激振力90度时,该测点达到相位共振。若结构上所有的测点皆满足上述条件时,结构以纯模态形式振动,此时的MIF值为1,这是一种理想情况。在试验中,MIF值总是小于1的,也就是无法完全达到相位共振,这是由多方面因素造成的,主要包括激振力无法完全平衡阻尼力,结构的非线性影响等等。MIF值也作为模态参数精确程度的一个参考标准[12]。
1.2 频率误差的分析原理
对于线弹性结构系统,加速度响应计算公式如下[13]
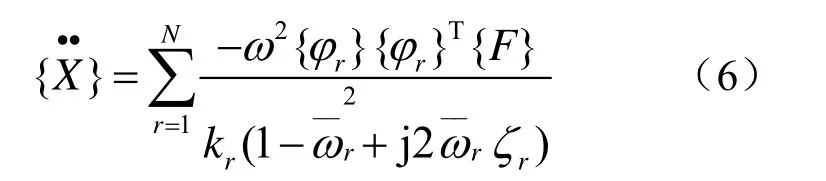
其中,ω为实测结构振动频率,ωr为第r阶模
结构的振动响应表现为结构各阶模态的叠加,各阶模态的贡献不同。在多点稳态正弦调谐模态试验中,调谐第r阶模态,结构的振动响应为第r阶模态和剩余模态(第1~r-1阶模态和第r+ 1 ~N阶模态)的叠加。当调谐满足要求时,MIF达到一个较高值,此时响应中第r阶模态占据主导地位,剩余模态的贡献为一个小量,忽略剩余模态的影响,得到加速度响应计算公式为:
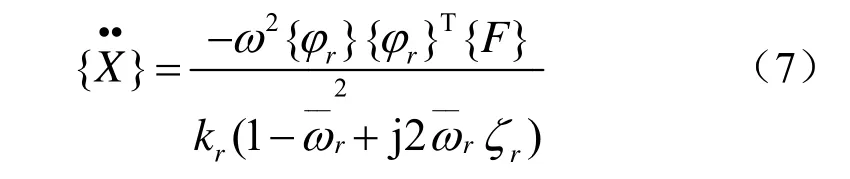
代入MIF 表达式,并化简得 第i点的加速度响应可以表示为
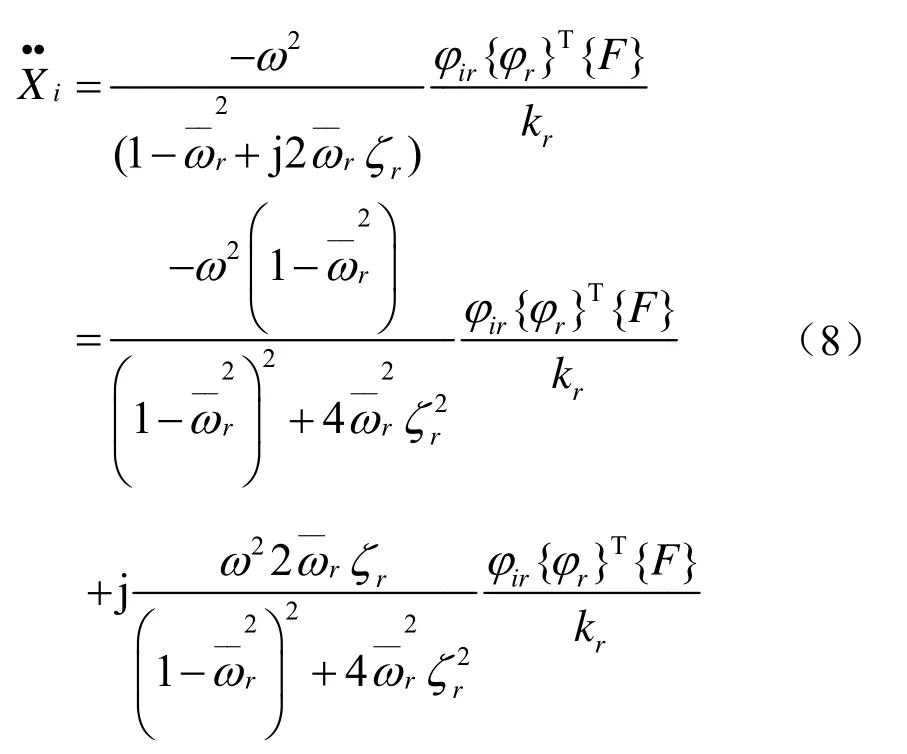
定义频率相对误差(以下简称为频率误差)为
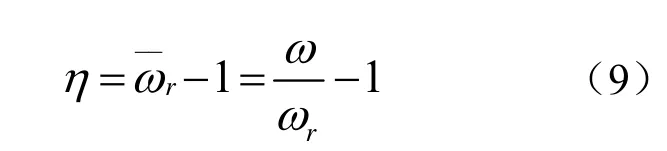
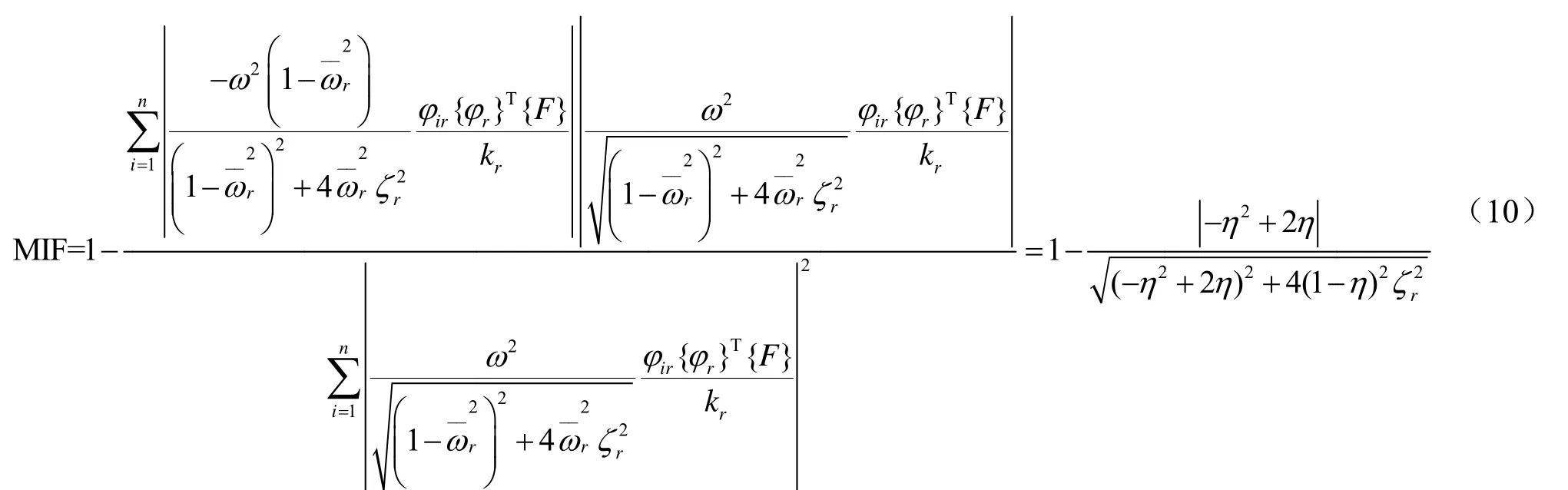
得到MIF与频率误差和阻尼比的显式解析关系式,也可表示为,即频率误差只与MIF值和第r阶模态模态阻尼比有关。
2 频率误差的分析方法
2.1 剩余模态影响小的情况
剩余模态影响小的情况如图1所示。
图1 剩余模态影响较小的频响曲线 Fig. 1 Residual modes have less effect on the frequency response curve
调谐第r阶模态,当MIF值足够高时,在分析第r阶模态时可以忽略剩余模态的影响,频率误差满足上述的MIF值解析关系式。
将MIF值随频率误差和阻尼比的变化关系绘成曲面图如图2所示。
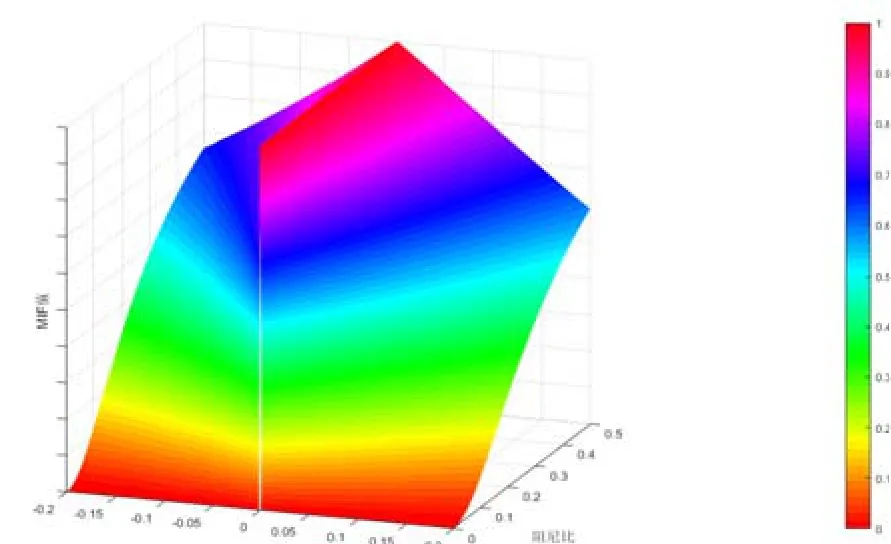
图2 “MIF—频率误差、阻尼比”曲面 Fig. 2 "MIF - Frequency error, Damping ratio" surface
分别取不同阻尼比,得到MIF—η曲线,如图3所示(从内到外,,阻尼比分别为0.005、0.008、0.01、0.03、0.065、0.1、0.5)。
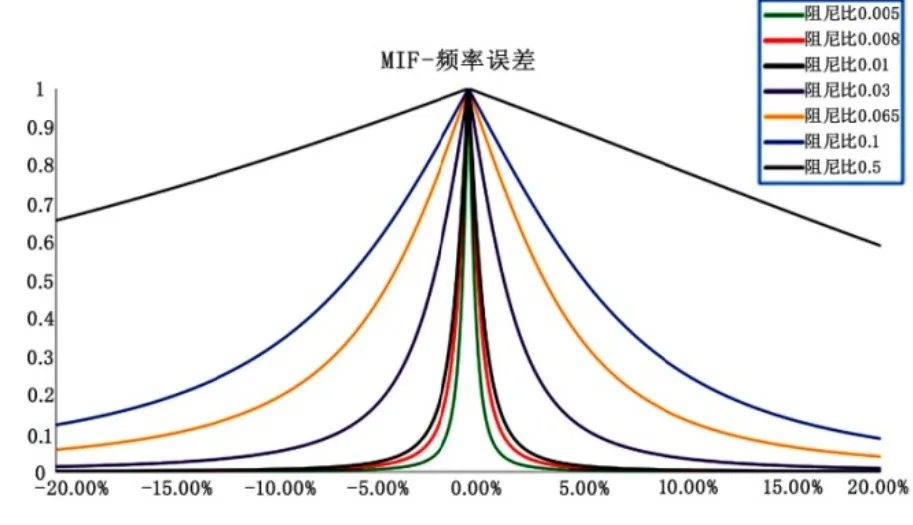
图3 “MIF—频率误差”曲线 Fig..3 "MIF-Frequency Error" curve
分别取不同的频率误差,观察MIF值随阻尼比的变化规律。在同一个频率误差下,阻尼比越大,MIF值越大,如图4所示(从左至右,频率误差分别为0.5%,1%,2%,3%,5%,10%)。在其中取部分点写入表1。
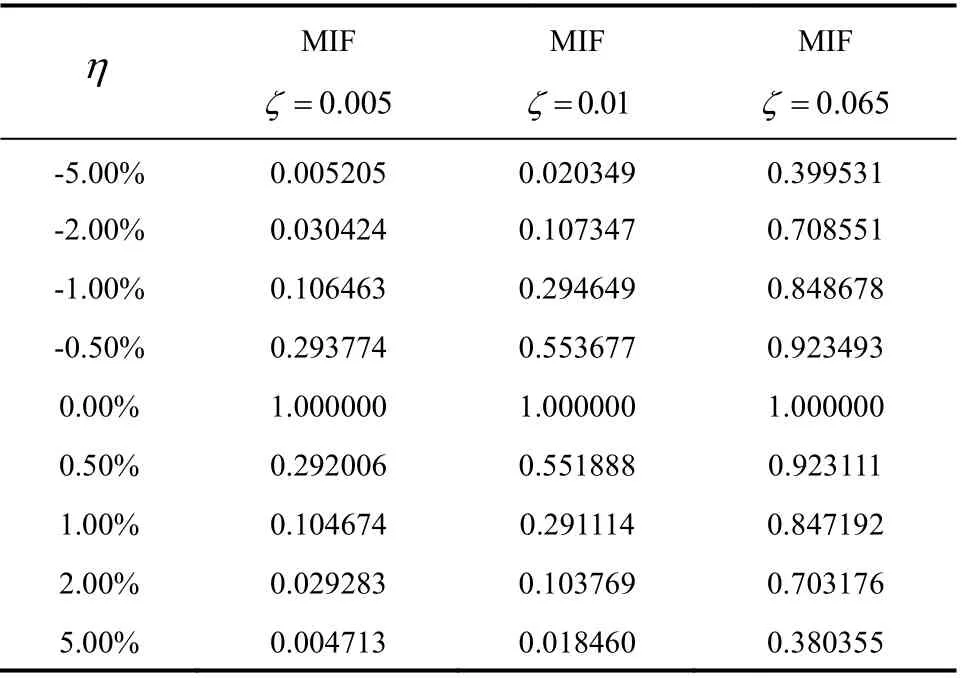
表1 各阻尼比下,各误差点的MIF理论值 Table 1 MIF theoretical value of each error point at each damping ratio

图4 “MIF—阻尼比”曲线 Fig.4 "MIF - damping ratio" curve
2.2 剩余模态影响大的情况
图5所示是剩余模态影响大的情况的频响曲线。此时,剩余模态的的贡献产生影响,第i点的加速度响应,如式(11)所示。
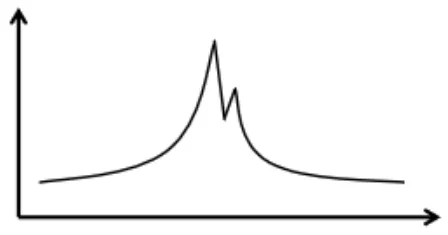
图5 剩余模态影响较大的频响曲线 Fig.5 Residual modal influences the frequency response curve
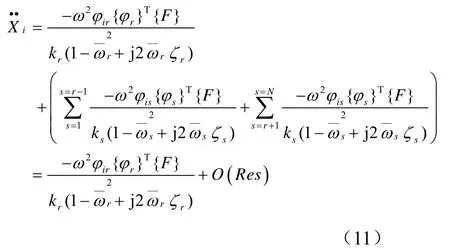
式中, O( Res)为剩余模态的影响,实际的MIF值应包含剩余模态的影响
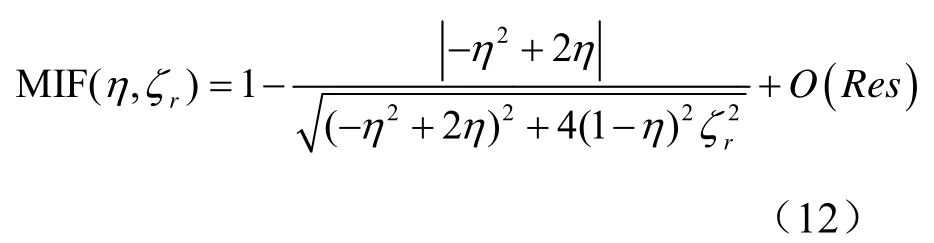
针对不同剩余模态的截断影响,需要建立不同阻尼比下的频率误差与MIF值之间的关系。
3 八自由度系统频率误差的仿真分析
考虑8自由度离散“质量—阻尼—弹簧”系统,两端固定,对其第一阶模态进行仿真。质量块的质量为m,弹簧的的刚度为k,阻尼系数为c。如图6所示

图6 8自由度系统模型 Fig.6 eight degrees of freedom system model
振动微分方程为
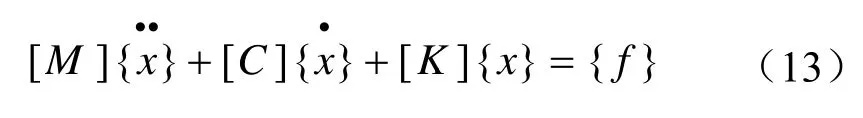

运用状态空间法,设状态量
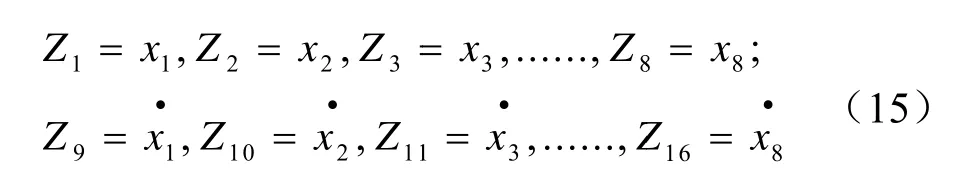
代入状态方程,输出量为加速度响应
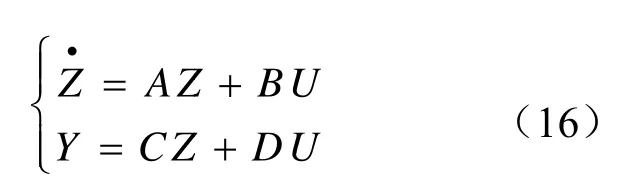
式中,A、B 、C、D矩阵分别为
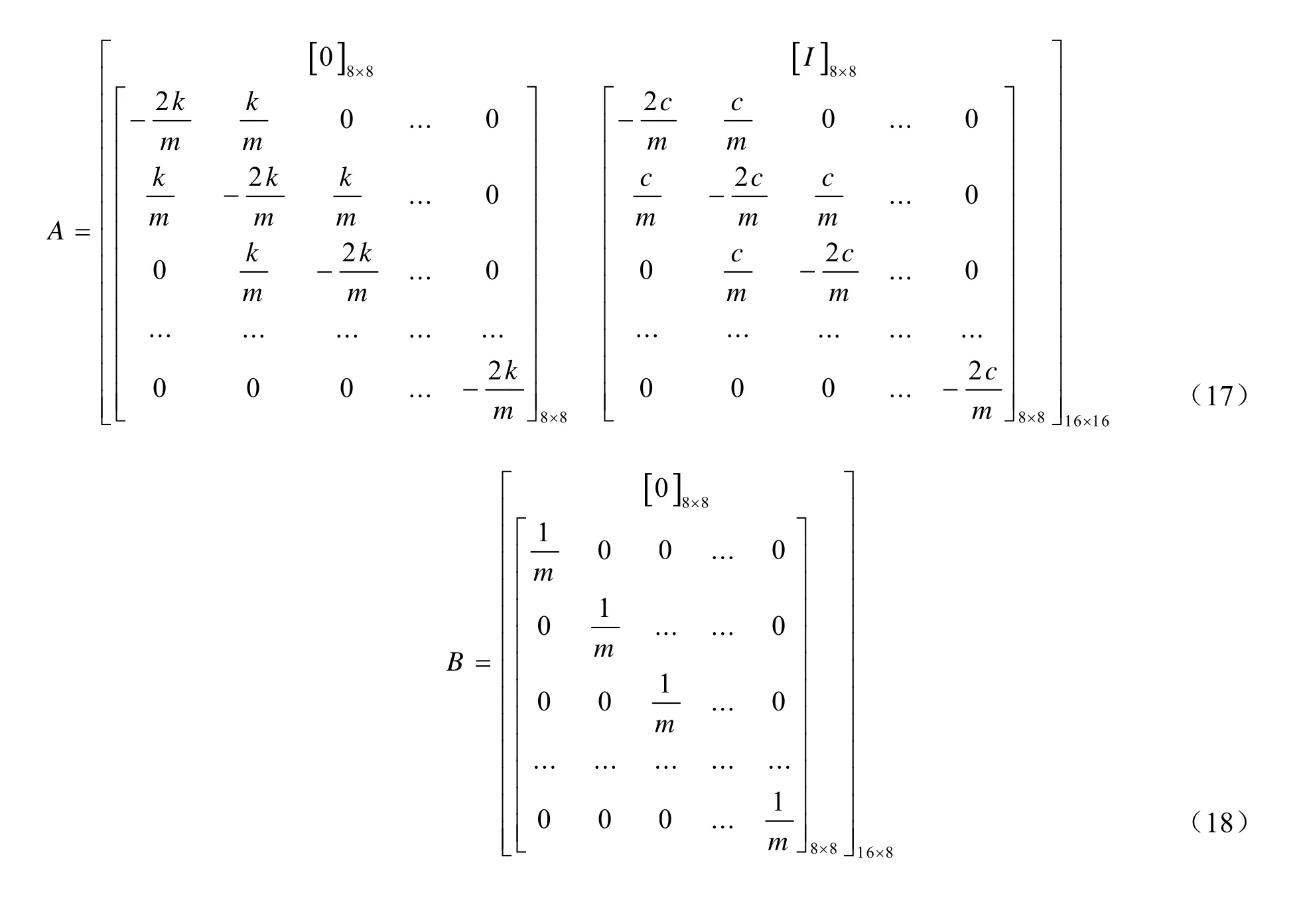
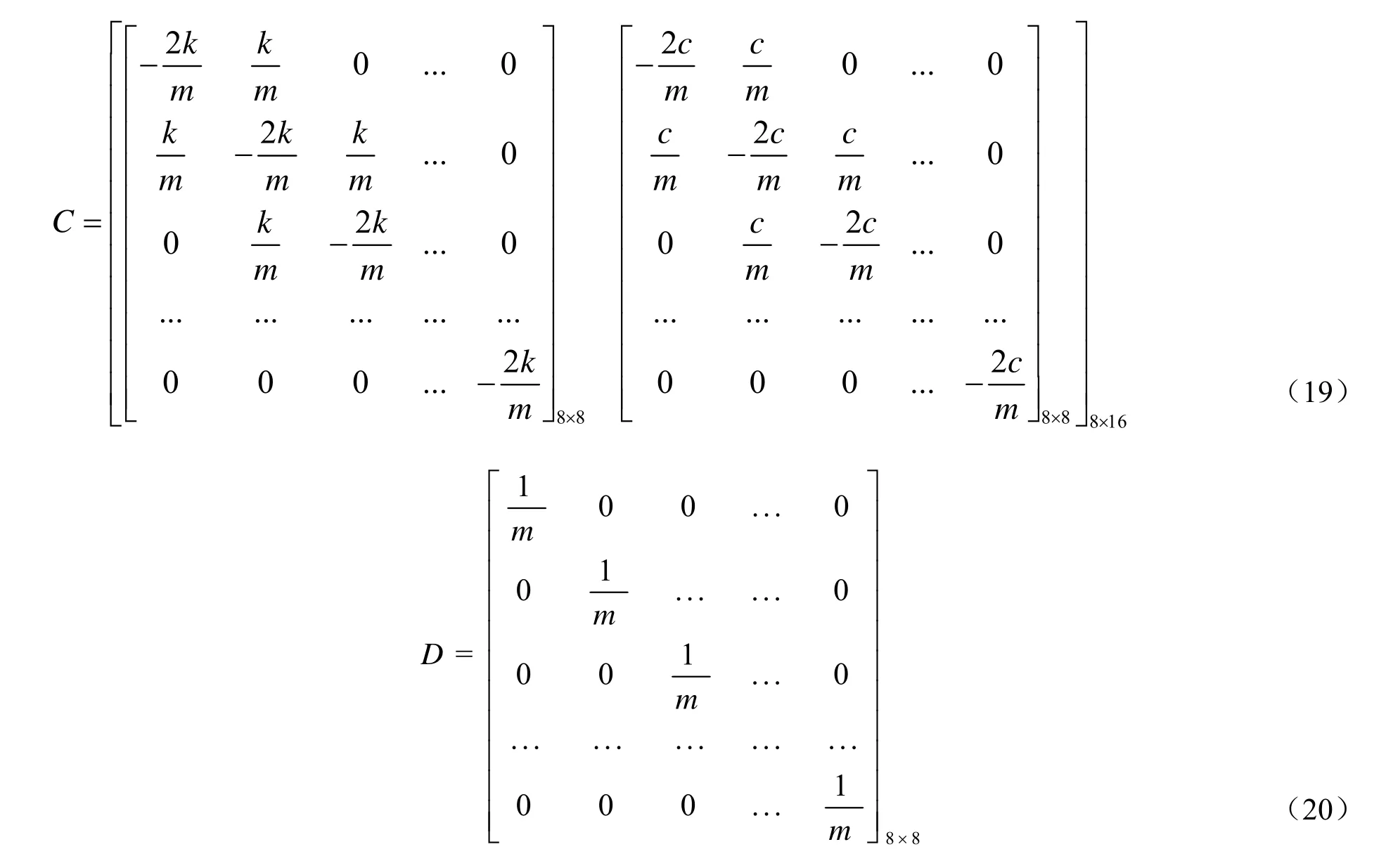
设置质量m=1,刚度k=100,则系统的第一阶模态频率为ω1=3.4729635(rad/s),第一阶模态振型为
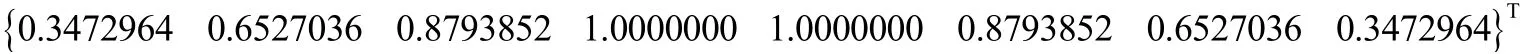
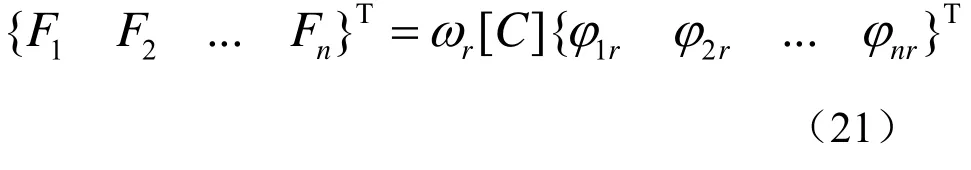
激振力的频率以第一阶模态频率 1ω为参考,引入适量误差,分析在不同频率误差下MIF值的变化规律。取不同的阻尼比,计算得到对应的阻尼系数代入阻尼矩阵。仿真得到8个测点的加速度响应的时域曲线,分别取各测点的稳态段数据,用正弦曲线进行曲线拟合,得到各个测点的幅值和相位数据,代入MIF值表达式,计算MIF值,如表2~表4所示。
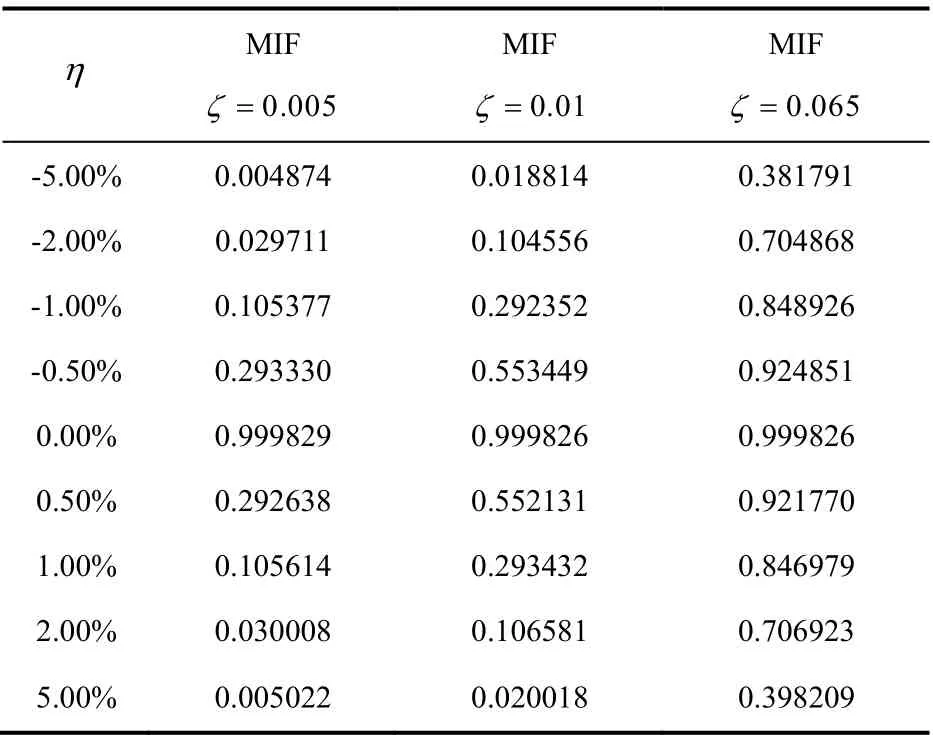
表2 各误差点的MIF仿真值(8点激振) Table 2 MIF simulation value of each error point (8-point excitation)
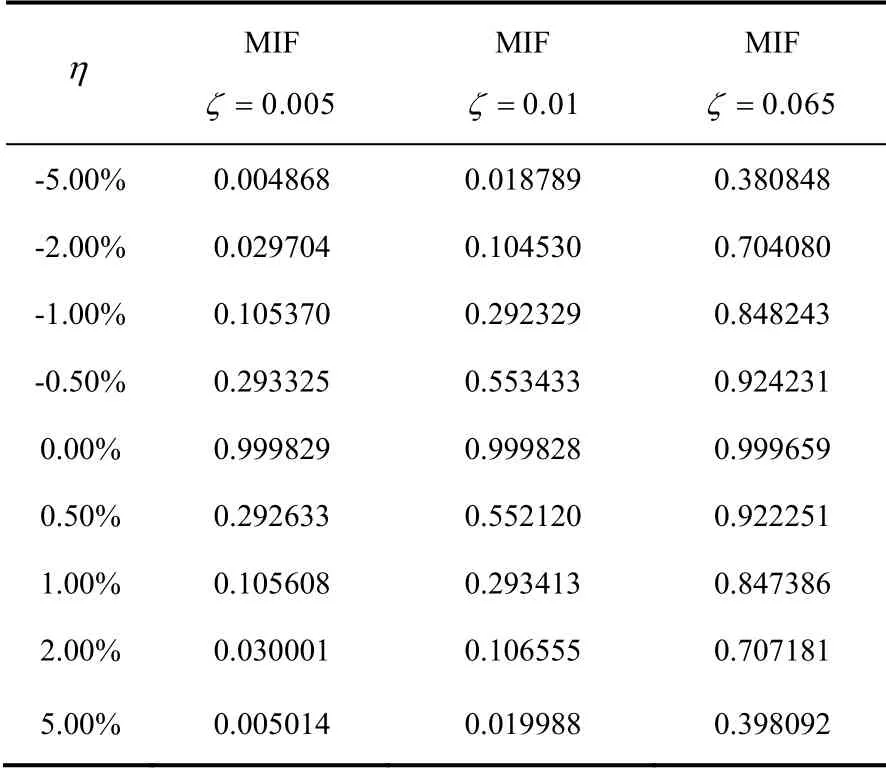
表4 各误差点的MIF仿真值(2点激振) Table 4 MIF simulation value of each error point)
针对第一阶模态,分别取阻尼比为0.005、0.01和0.065,激振频率 Tω分别取为 1(15%)ω- 、(1- 2%)ω1、 (1- 1 %)ω1、 (1- 0.5%)ω1、ω1、(1+ 0.5%)ω1、(1 +1 %)ω1、(1 + 2%)ω1、(1 + 5%)ω1,根据激励点数量和位置的不同,分为以下三种情况:1)在8个点全部施加激励;2)在4个点(1、3、5、7)施加激励;3)在2个点(1、8)施加激励。
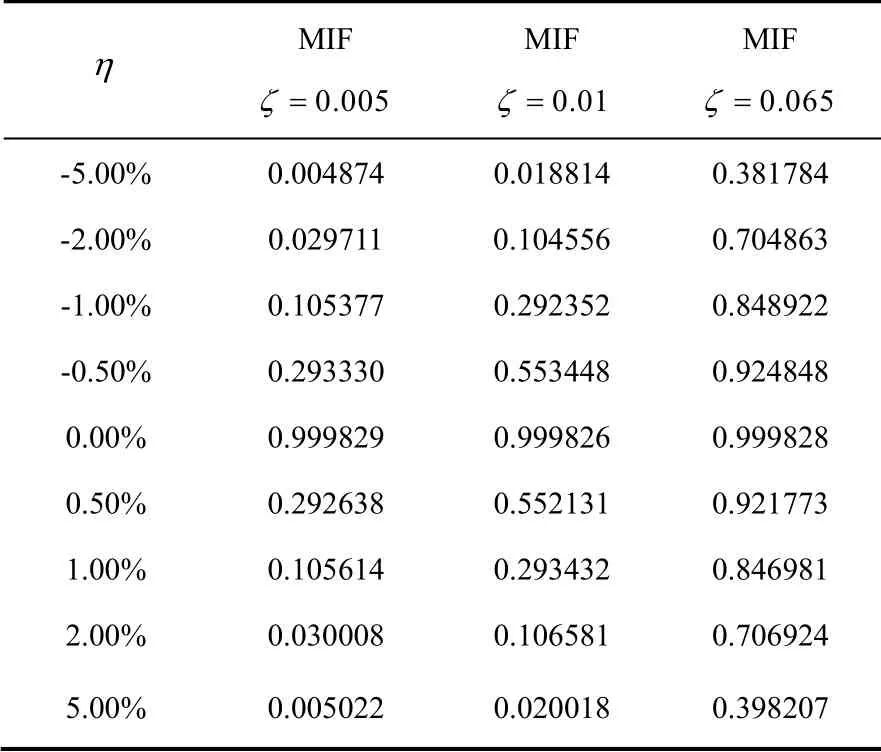
表3 各误差点的MIF仿真值(4点激振) Table 3 MIF simulation value of each error point
对比仿真值与理论曲线,如图7、图8和图9所示。
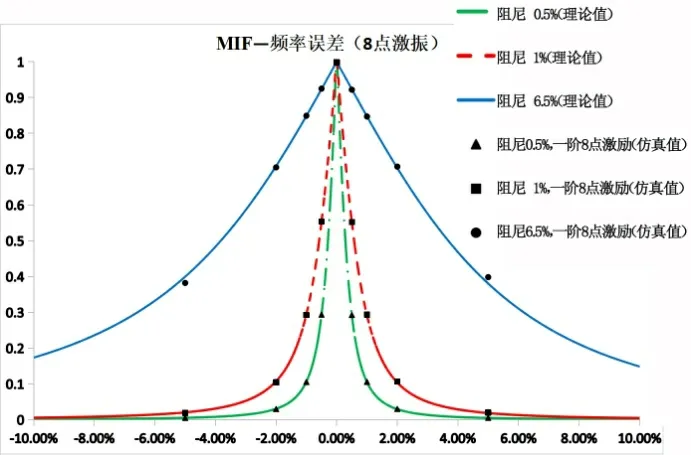
图7 MIF仿真值与理论值对比(8点激振) Fig.7 Comparison between MIF simulation value and theoretical value (8-point excitation)
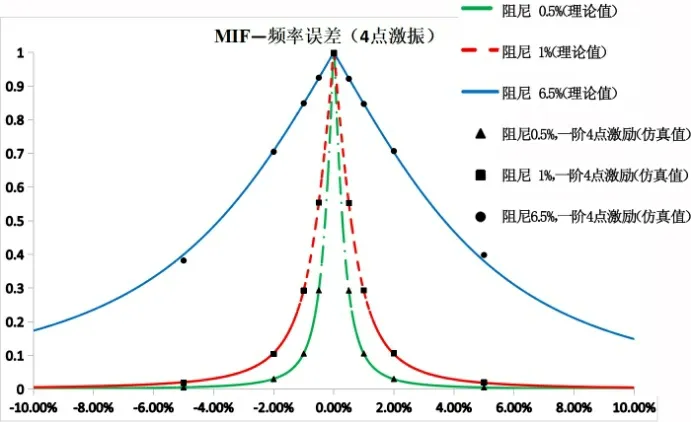
图8 MIF仿真值与理论值对比(4点激振) Fig.8 Comparison between MIF simulation value and theoretical value (4-point excitation)
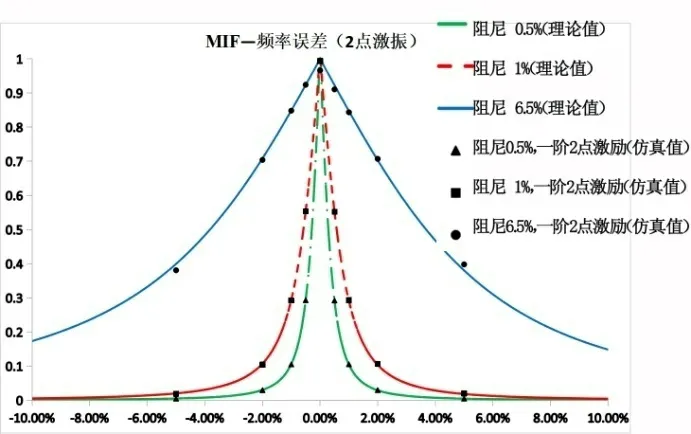
图9 MIF仿真值与理论值对比(2点激振) Fig.9 Comparison between MIF simulation value and theoretical value (two-point excitation)
在图10中,横坐标为频率误差,纵坐标为MIF仿真值(包含剩余模态的影响)与MIF理论值(不包含剩余模态的影响)的偏差。由图10可知,仿真值与理论值基本吻合。在频率误差较小时,模态纯度较高,剩余模态影响较小,仿真值与理论值吻合程度很好。在频率误差增大时,剩余模态的影响也随之增大,在大阻尼比情况下更容易看出这个微小影响。
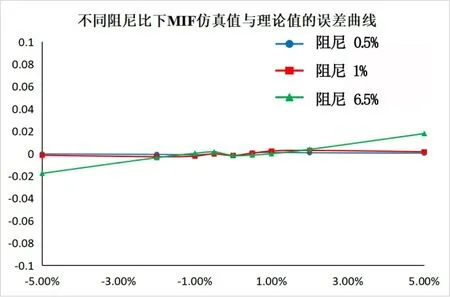
图10 三种阻尼比下MIF的仿真值与理论值的误差曲线 Fig.10 Under three damping ratios, simulation values of MIF and the theoretical values of MIF
4 结论与展望
本文以多点稳态正弦调谐模态试验和模态纯度指示函数为基础,建立了频率误差分析原理,提出了频率误差分析方法。运用状态空间法仿真八自由度系统,频率误差的仿真值与理论曲线一致,表明了频率误差分析方法的可行性。下一步开展针对连续弹性系统的研究,进行频率误差的分析与仿真,并进行实验验证。

