基于线控电子液压制动系统的车辆减速度控制
唐派,熊璐,李军,舒强,冷搏
(1.重庆交通大学机电与车辆工程学院, 重庆 400074;2.上海同驭汽车科技有限公司, 上海 201800;3.同济大学汽车学院,上海 201804)
0 引言
随着当前车辆的电动化、智能化发展不断加深,毫无疑问对车辆行业提出了更高的要求。对于我国汽车行业而言机遇和挑战并存,在众多难点中制动系统的电动化转变至关重要。
传统车辆使用真空助力器提供制动助力,但是新能源车型没有能够直接提供真空度的发动机,所以需要额外的真空泵、储气罐等设备,此方案存在工作噪声大的问题影响整车舒适性。并且在制动能量回收方案设计上,真空助力器方案只能在液压制动上叠加电助力,降低了制动能量回收率,同时存在着影响驾驶员制动踏板感的问题。
此外,自动紧急制动(autonomous emergency braking,AEB)、自适应巡航控制(automatic cruise control,ACC)等各类高级驾驶辅助功能(advanced driver assistant system,ADAS)也对车辆纵横向控制性能提出了更高的要求。传统制动系统采用真空源提供制动助力的方案存在连续建压能力不足的缺点。同时线控建压响应较难满足紧急制动的响应时间要求。
基于传统执行器开展的减速度控制研究较少,多数利用高压蓄能器的主动建压能力实现AEB功能。马国成等基于ESC执行机构,以减速度作为控制目标,对液压力进行控制。根据电磁阀开闭的非线性特性,基于分段设计的思想在不同特性下采用不同的PID参数以期实现对压力的准确控制。但重点在压力控制部分,车辆减速度控制并未过多体现。
当前也有部分学者基于线控制动系统开展减速度控制研究。张东利用相关执行器,根据行车过程中自车与前车安全距离作为控制目标,设计AEB触发时机。但是仅设计了紧急制动工况的减速度控制,缺乏对减速度控制精度、超调特性、响应时间的研究,也没有考虑道路坡度因素对减速度控制的影响。
为了尽量消除道路纵向坡度对于车辆动力学控制的扰动,雍文亮等利用车辆动力学和加速度传感器两个信息源,采用基于Kalman滤波器的融合算法对道路坡度进行估计。
综上所述,当前学者对于新型制动系统的研究重点集中于压力控制。此外,在设计用于整车减速度控制的动力学模型时,并未考虑坡度因素对减速度控制的影响。鉴于此,文中基于EHB优异的液压控制性能,设计考虑道路坡度因素的减速度控制模型,并采用模糊PID控制方法提升了减速度控制鲁棒性。
1 线控电子液压制动系统介绍
线控电子液压制动(electro-hydraulic braking,EHB)系统由电机、控制器、减速机构、制动主缸等部件组成,如图1所示。电机扭矩经过蜗轮蜗杆、齿轮齿条传动副实现减速增扭,并且将电机的转动转化为齿条的平动,从而推动主缸活塞完成建压。

图1 EHB总成
EHB使用机械解耦的方案,驾驶员通过制动踏板输入-液压力输出关系解耦,可以实现更高自由度的制动能力回收的同时保持整车减速度。同时,利用踏板感觉模拟器使得驾驶员制动脚感与传统真空助力器制动脚感保持一致。
当前量产车型的各类高级驾驶辅助系统功能多使用车身稳定控制系统作为线控液压执行器。由于ESP主动建压依靠柱塞泵,而EHB通过永磁同步电机建压,在建压速度、最大建压能力、最大保压时间、循环使用寿命等方面的关键指标均优于ESP。EHB与ESP建压性能对比见表1。
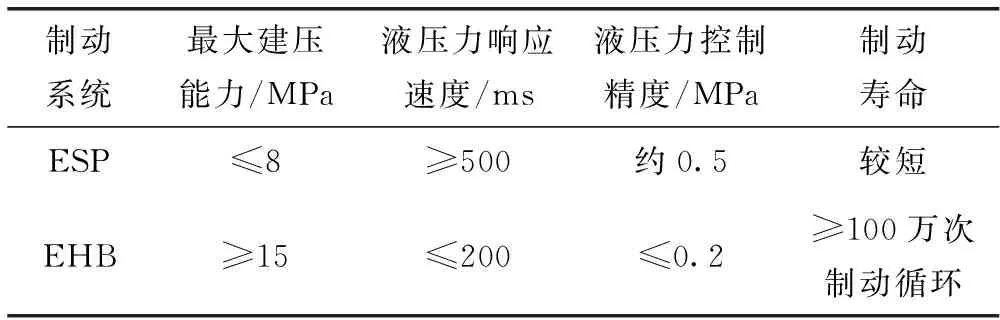
表1 EHB与ESP建压性能对比
2 车辆动力学建模
本文所建立的车辆纵向制动减速度控制策略如图2所示。

图2 减速度控制策略
图中:为坡度阻力;为空气阻力;为滚动阻力;为加速阻力;为目标减速度;为实际加速度;为目标液压力。
汽车行驶驱动力-阻力平衡方程为:
=+++;
(1)

(2)
式中:为驱动力;为发动机输出扭矩;为变速器传动比;为减速器传动比;为机械效率;为重力;为道路坡度;为空气阻力系数;为迎风面积;为车速;为旋转质量等效系数;为车辆质量。
以下对道路阻力、制动器模型以及EHB建压特性进行分析。
2.1 车辆道路阻力求解
实车测试中,空气阻力和滚动阻力可以通过实测空挡滑行测试直接求解。使用表示此两项的值,则=+。通过在不同初始车速下挂入N挡滑行,得到道路阻力MAP,如图3所示。

图3 道路阻力MAP
拟合方程为:

(3)
2.2 制动器建模
试验车辆基础制动器部分参数见表2。

表2 制动器部分参数
根据以上参数利用式(3)可以计算出制动扭矩
=2π4。
(4)
式中:为制动力矩;为摩擦因数;为系统液压力;为轮缸直径;为轮缸数量;为制动半径。
通过计算,同时采用实际测试的方法进行验证:以60 km/h初速度建压,施加固定液压制动到车速为零,从0.5 MPa开始每间隔0.5 MPa测试1次,每组测试3次。减去所求解的道路阻力产生的减速度,求解得到液压力-减速度的对应关系,如图4所示。

图4 液压力-减速度的对应关系
由图4可知,实际测试结果和理论计算结果是一致的,验证了试验结果的可靠性。
2.3 EHB液压力控制性能分析
在各种液压力控制工况中,阶跃响应是对EHB液压力控制性能要求最为严格的工况,在要求响应时间的同时,不允许系统存在过大超调。但图5中高液压阶跃响应下存在的“超调”是由于管路节流特性所决定,并非真实系统超调。
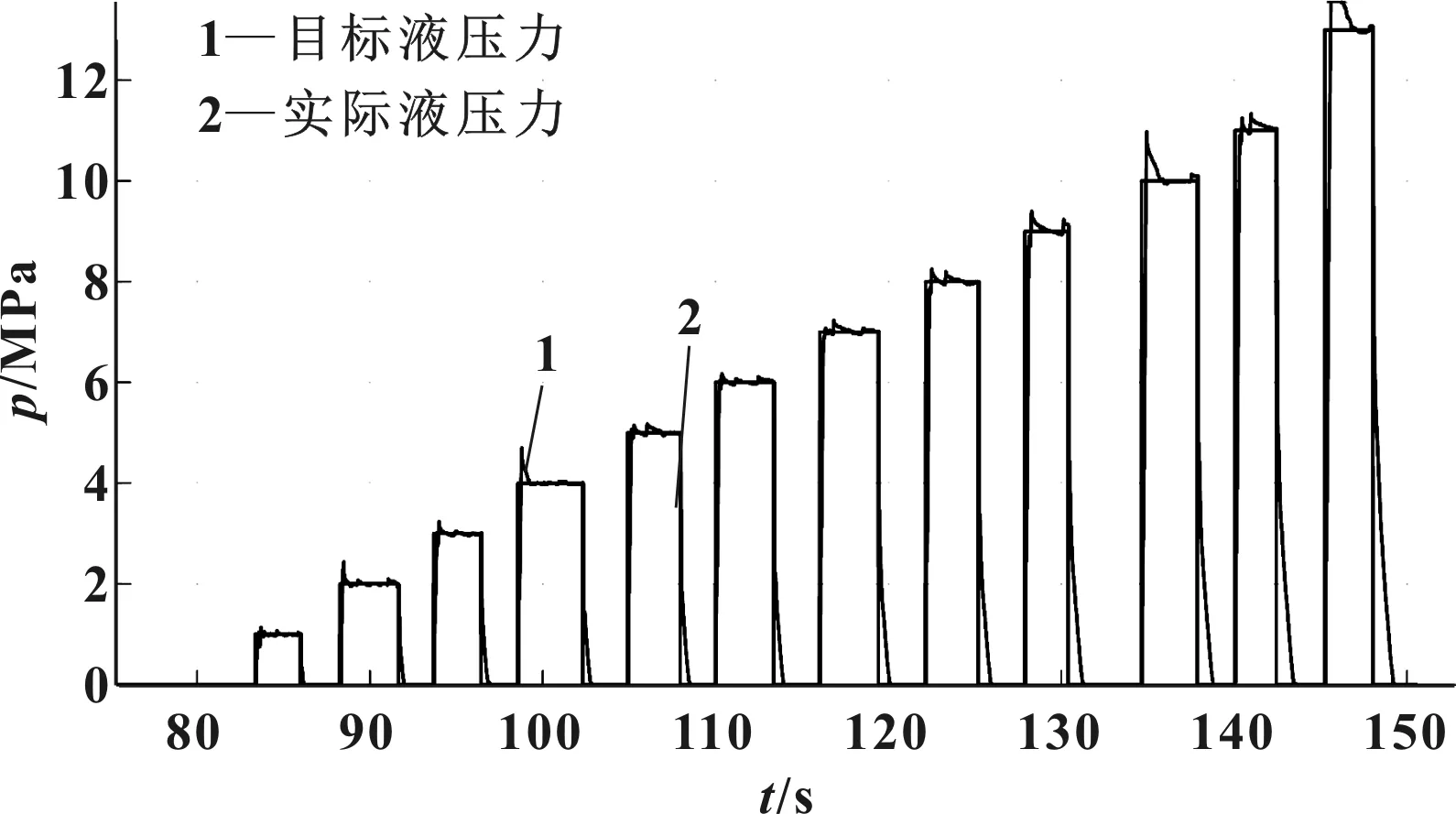
图5 EHB线控阶跃液压测试
测试结果表明,EHB阶跃液压力10 MPa下响应时间小于200 ms。在阶跃测试下通过参数辨识将液压力控制系统认为是二阶系统,求得EHB建压性能传递函数为:

(5)
2.4 仿真与实测结果对比
采用液压力开环测试,给定单位阶跃目标液压,测试整车减速度响应。实际测试中记录加速度传感器信号,并且使用轮速信号差分求解轮减速度,利用Garsim得到仿真和实际测试对比结果,如图6所示。
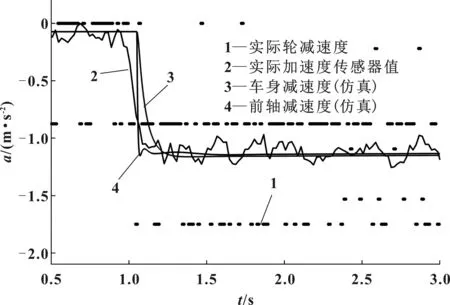
图6 阶跃减速度仿真实测对比
由图6可知,受总线通信速率以及传感器精度影响,实际计算的轮减速度误差较大,在稳态情况下存在1 m/s的误差。通过对比Carsim模型仿真结果和真实测试结果,可以确认所建立的车辆动力学模型的准确性。
3 基于Kalman的坡度估计
坡度会在很大程度上影响减速度控制精度,有必要对此进行估计。当系统为线性系统,并且噪声具有独立性时,可以使用Kalman进行参数估计。
离散Kalman公式如下:

(6)
式中:(|-1)为先验估计值;为状态转移矩阵;(-1|-1)为上一时刻最优估计;为控制矩阵;()为系统控制参数;(|-1)为协方差矩阵;(-1|-1)为协方差矩阵更新;为系统建模误差;为观测误差;()为Kalman增益;()为系统观测参数;为系统观测矩阵。
利用加速度传感器信号原理可知,得到车辆实际加速度后便可以获得坡度信息:
=+sin。
(7)
由此建立Kalman过程方程(8)和观测方程(9):
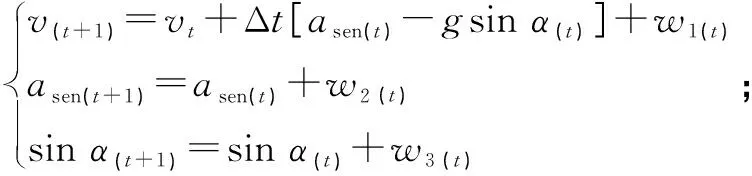
(8)

(9)
根据真实传感器模型构建和矩阵分别为:
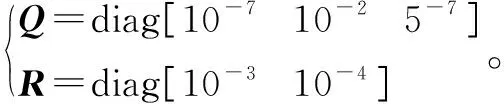
(10)
与一阶低通滤波器进行坡度计算的结果进行对比,低通滤波器计算公式为:

(11)
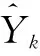
图7为坡度估计结果对比,其中Raw值为原始数据直接求得的结果。为方便观测,选取纵坐标为gsin,即重力在坡道方向的分量,表示坡度。

图7 坡度估计结果对比
由图7可以看出,使用基于Kalman的坡度估计方法在保证坡度估计准确性的情况下,相比于采用一阶滤波方法,可以提高响应速度。由曲线1可以看出,采用传统一阶滤波方法,必须采取极高的截止频率才能过滤掉此类噪声,但会引入较大的延迟。
4 减速度闭环控制方法
传统PID控制方法计算公式为:
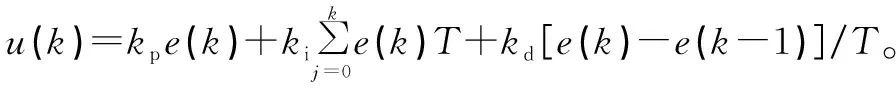
(12)
式中:为比例系数;为微分系数;为积分系数;为采样周期;()为误差;为积分周期值。
采用传统控制方法无法满足车辆在不同目标减速度下响应的一致性要求,由此文中采用模糊PID控制方法。模糊控制将输入量模糊化,通过已知特性得到的经验规则计算得到模糊化的输出量,最终通过求解模糊方程得到精确的控制输出量。
使用减速度控制量()=-和减速度变化率Δ()=()Δ作为模糊控制器的输入,求解目标液压力。
根据实车标定测试,确定()为:
[-0.2 -0.5 -1 -2 -3 -4 -5]。
Δ()范围为:
[-15 -10 -5 -3 0 3 5 10 15]。
两者的模糊域都设置为[],构建模糊控制规则,最终转化为MAP图,如图8所示。

图8 模糊PID MAP图
仿真试验验证采用阶跃减速度测试,结果如图9和图10所示。

图9 PID-模糊PID减速度控制对比
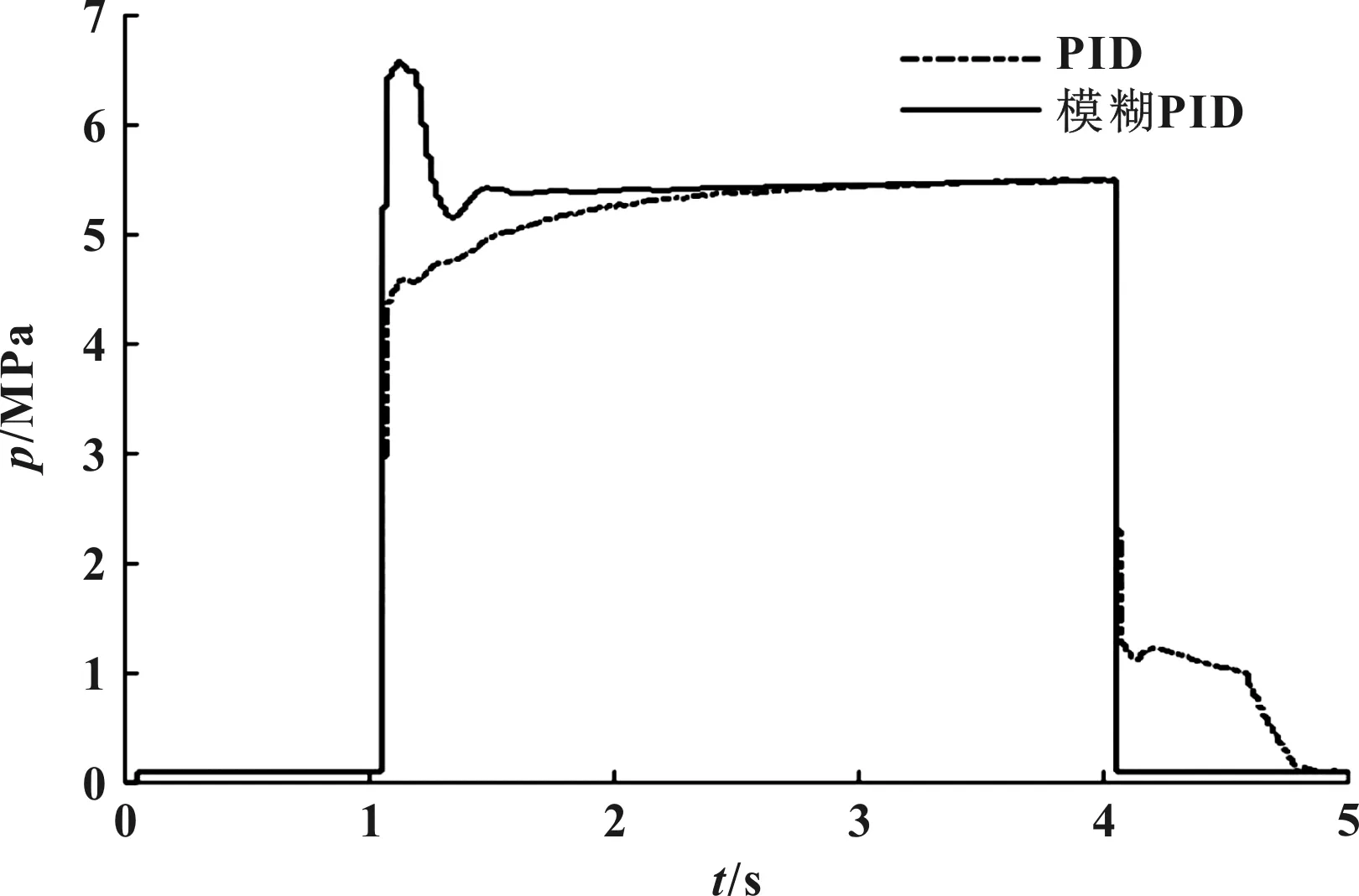
图10 PID-模糊PID液压控制对比
由图可以看出采用模糊PID后,在对于响应要求更为严苛的阶跃减速度测试下,由于模糊PID能够有效利用反馈信息,所以使得减速度响应时间得到有效提升。PID-模糊PID性能对比结果见表3。

表3 PID-模糊PID性能对比
5 结语
文中基于EHB优异的液压力控制性能,设计了用于车辆减速度控制的车辆动力学模型。并且在PID控制基础上,设计了适用不同减速度控制工况下的模糊PID控制器,得出了以下结论:
(1)基于理论和实际测试互相参考,对车辆行驶过程中的道路阻力进行了精确的计算,并通过了试验验证。
(2)利用Kalman进行道路坡度估计降低了坡度估计的延迟。
(3)采用模糊PID的控制方法,相比于传统PID控制方法,提高了减速度控制的响应时间。

