基于加权关联规则的数据共享效果跟踪方法设计

刘 亚 男

(安徽工商职业学院，安徽 合肥 231131)

0 引 言

数据共享是指通过数据分析，根据数据规律使数据在不同服务器间交互的过程，是知识发现领域的重要应用技术。数据共享过程包括数据采集、统计、分类、上传等[1-2]。利用数据共享跟踪算法，有效获取相关数据，可以减少人力、物力资源的消耗，提高决策效率。随着数据量不断扩增，研究提高数据共享跟踪效果的运行效率与跟踪结果的精准度的算法具有重要现实意义[3-4]。

当前已经有很多专家和学者提出了较好的数据共享算法[5]。如：高峰提出了一种大数据分析的数据交互共享平台，通过对数据的自适应调度优化，对共享数据库进行设计[6]，但该方法对数据的分类不够精细，导致共享效果跟踪准确度较低。李云飞提出利用自适应调度加权系数对数据进行模糊聚类控制，以完成数据的共享存取[7]，但该方法的模型构建过程复杂，降低了算法的跟踪效率。杨蕴睿提出分析数据的特征，通过正交加权约束均衡比改进蚁群算法，结合蛙跳算法得到数据最优共享[8]，但该算法所需的跟踪时间较长，且汇总分析过程复杂。

针对上述方法存在的问题，提出一种基于加权关联规则的数据共享效果跟踪算法。应用模糊关联规则来改善数据分类的分区界限过硬问题，通过数据空间映射关系与数据跟踪因子的结合，获取在相同维度与不同维度内数据空间的数据跟踪算法。

1 基于加权关联规则的数据共享效果跟踪方法

1.1 基于模糊理论的数据共享效果加权关联规则

一般情况下，各类信息数据共享效果之间或多或少地存在某种内在或外在关联，在进行数据共享效果跟踪前，须要对获取的数据进行关联规则分析，分区处理获得的数据，并进行转换，变换为二值型。为不使分区的数据之间的边界过于硬化，用融合模糊理论来软化数据划分的边界[9]。

模糊理论的运算过程是以模糊集合为基础将数据信息进行严密量化，并将量化后的数据元素划分为模糊数据集合，设定义域为U，对于U内的某一属性模糊集合A都有一个与之对应的实值函数。当u∈U，函数值μA(u)可表示u隶属于属性集合A的程度，函数μA为属性模糊集合A的隶属函数。通过隶属函数值来衡量元素隶属于集合A的程度，隶属函数值越趋近于1，说明元素对于集合的隶属度越高；隶属函数值越趋近于0，说明元素对于集合的隶属度越低；当隶属函数值为0时，则可认为该元素与集合间不存在关联，即元素完全不属于集合。

模糊加权关联规则的描述形式为X-A⟹Y-B，其中，集合X表示加权关联规则的前导，集合Y表示加权关联规则的后续，X,Y⊆I且X∩Y=φ，I为数据库不可再分割的项集。属性模糊区间集合A、B分别为A={a1,a2,…,ap}⊆R、B={b1,b2,…,bq}⊆R，R={r1,r2,…,rh}为包含h个差异化模糊区间的集合。A、B中的区间ai、bj分别为集合X与Y中元素xi、yj所对应的模糊区间。

设UA(X)=Λμai(xi)为集合X对于模糊区间集合A的隶属函数值，每一个元素xi在模糊区间集合A中都仅有一个模糊区间ai与之对应，μai(xi)为元素xi隶属于模糊区间ai的程度。通过上述分析，得到数据共享效果的数据集模糊加权关联支持度ES(X-A⟹Y-B)的计算式为

(1)

其中，|D|为数据库的数据值，UB(Y)=Λμbj(yj)为集合Y对于模糊区间集合B的隶属函数值。数据集模糊关联置信度FC(X-A⟹Y-B)的计算式为

(2)

利用公式(1)、公式(2)计算数据共享效果分类间的模糊加权关联支持度与置信度，并根据计算结果对数据分类进行调整，为数据共享效果的跟踪奠定基础。

1.2 基于加权关联规则映射的数据共享效果跟踪算法

将数据共享效果的数据看作分布在多维子空间不同维度内的点，对于不同子空间维度内的数据，仅考虑数据对应维度之间的关联性即可；对于子空间同一维度内的数据，需要根据加权关联规则来计算数据间的关联程度，对数据进行归类划分，完成数据共享效果跟踪。

设d′表示数据的子空间维度，先对分布在多维子空间不同维度内的共享效果数据集进行数据挖掘，数据分布的多维子空间描述矩阵M为

(3)

设分布于不同子空间维度内的2个数据集分别为Vk1和Vk2，对应的子空间维度分别为Mk1和Mk2(k1,k2≤d′)，子空间维度Mk1和Mk2之间欧式距离[10]为D(k1,k2)，数据集Vk1和Vk2之间的欧式距离为d(k1,k2)，通过下式对分布在不同空间维度内的数据集进行挖掘：

(4)

其中，M为多维子空间矩阵，δ为多维子空间的数据跟踪算子，P(Vk1)为数据集Vk1的数据跟踪频率，P(Vk2)为数据集Vk2的数据跟踪频率,ES、FC分别表示数据集的模糊加权关联支持度与置信度。

根据关联状况划分不同的数据集，则多维子空间中，一个维度内的数据集Vl1和Vl2之间的相关因子g(l1,l2)的计算式为

(5)

(6)

其中，P(Vl1)为数据集Vl1的数据跟踪频率，P(Vl2)为数据集Vl2的数据跟踪频率，eg(l1,l2)表示数据相关因子为g(l1,l2)时对应的跟踪算子。

设同一空间维度Mk内各数据集间的相关程度的设置阈值为T(V)，则

当g(l1,l2)>T(V)时，说明2个数据集之间的关联程度较强，2个集合的区分公式为

(7)

(8)

其中，n为同一维度内的数据集总量，Vls表示该维度内的第s个数据集，P(Vls)为数据集Vls的数据跟踪频率。

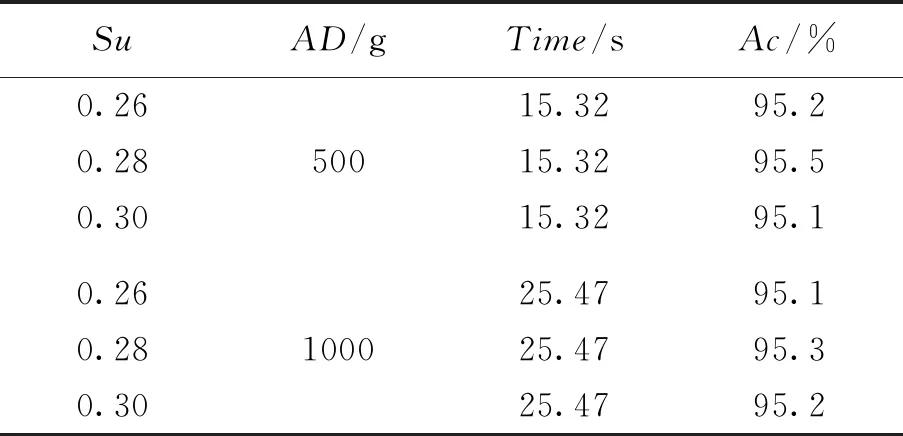
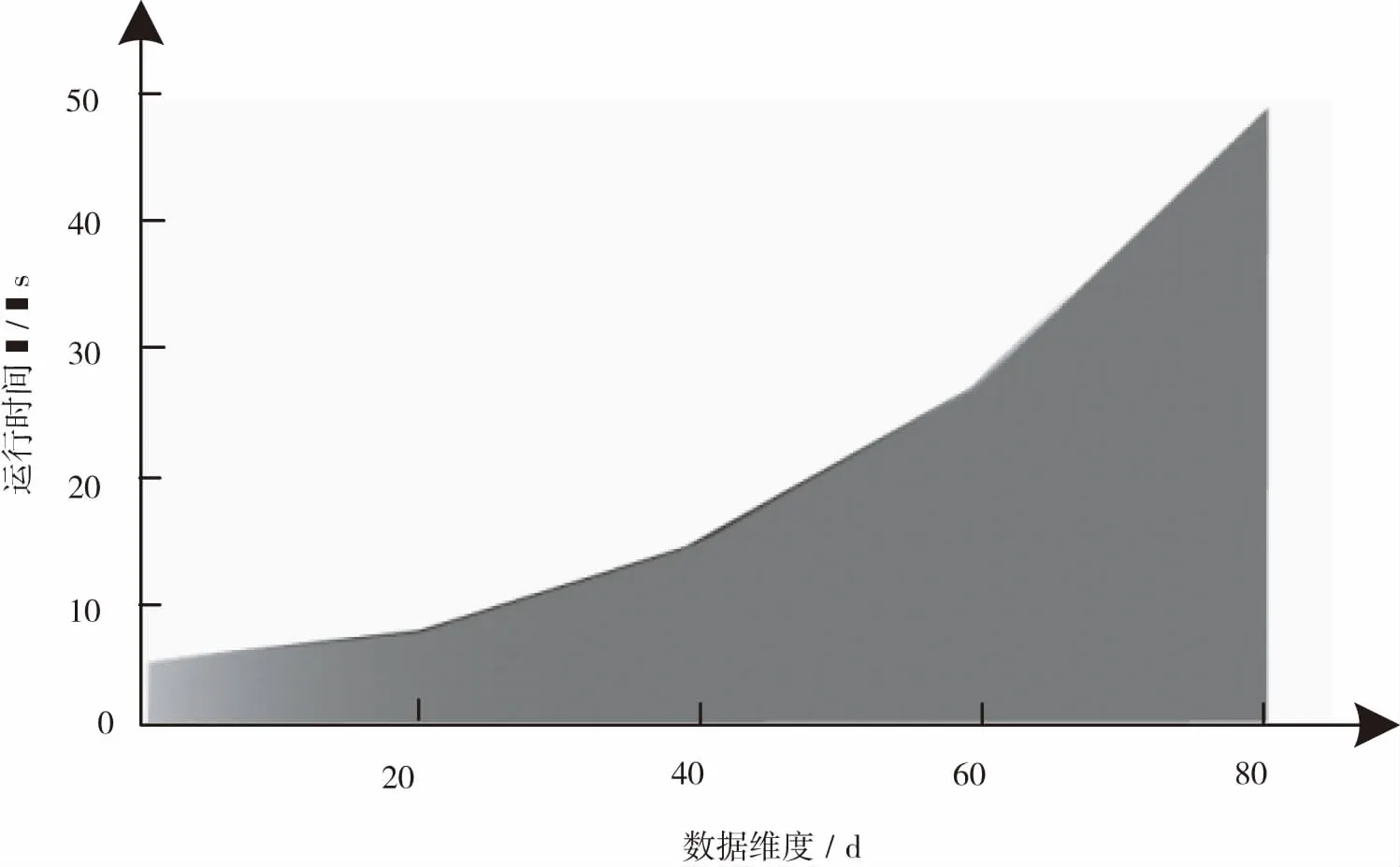
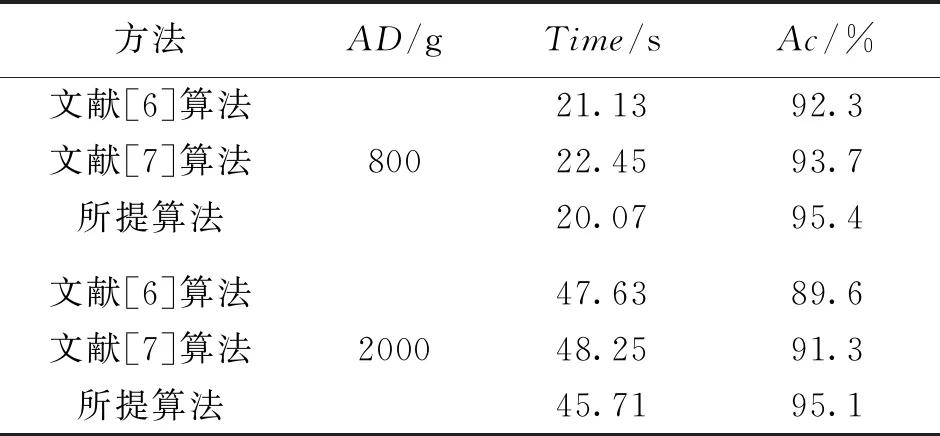
当g(l1,l2)

(9)

(10)

其中，e为2个数据集间的区分误差。

以模糊加权关联分析为基础，结合数据空间映射关系和数据跟踪因子，得到数据共享效果跟踪算法的计算公式。利用公式(4)实现空间不同维度内数据跟踪，利用公式(6)实现同一维度内的数据跟踪，并通过公式(7)～(10)来区分同一维度内不同关联强度的数据集，实现不同数据集的有效共享效果跟踪。

2 实验结果与分析

为了验证所提基于加权关联规则的数据共享效果跟踪方法的综合有效性，通过MATLAB仿真平台进行对比实验。实验操作环境为PC机(Windows 7系统)，CPU(Intel core i5)，主频(2.26 GHz)，ROM存储(6 GB)，存储(32 GB)，数据库(SQL Server 2008)，算法通过C++Builder实现。

采用所提基于加权关联规则的数据共享效果跟踪方法进行实验，对比加权关联规则的支持度变化对算法数据跟踪性能的影响，实验数据量为1 000个，实验结果见表1。表1中，Su表示加权关联规则的支持度，AD表示实验数据量，单位为个，用g表示；Time表示数据跟踪运行时间，单位为秒，用s表示；Ac表示数据跟踪结果的准确度，单位为%。

表1 加权关联规则支持度与算法性能

分析表1数据可知，当数据量一定时，算法运行时间不随加权关联规则支持度的变化而变化，说明加权关联规则的支持度对算法的数据跟踪效率无影响；对比数据量相同时所得数据跟踪结果的准确度，准确度随着加权关联规则支持度的变化而变化，数据量为500个和1 000个时，跟踪结果的准确度都大于95%，且在加权关联规则支持度为0.28时，跟踪结果的准确度最高，说明加权关联规则的支持度对跟踪结果的准确度存在一定影响。根据实验结果，以下实验中，选取加权关联规则置信度为0.28进行实验。

数据共享效果跟踪结果的准确度与数据维度划分为正相关关系，采用所提方法进行实验，实验中将数据共享效果数据分为不同数量的数据维度，观察该方法的运行时间与数据空间维度之间的关系，对比结果如下图1。图1中，横坐标为数据维度，设其单位为d；纵坐标为算法运行耗费的时间，单位为s。

图1 算法运行时间与数据维度的关系

由图1可知，随着数据的量和维度的增长，算法的运行时间也呈现线性增长。数据维度为20 d时，运行时间为8 s；数据维度为40 d时，运行时间为15 s；数据维度为60 d与80 d时，运行时间分别为28 s和50 s。分析以上数据可得到以下结论：数据维度越大，算法运行时间越长，且时间增长幅度也随之增大。根据这一结论，进行数据跟踪时，应结合实际需求对数据进行适当的维度划分，保证算法的跟踪效率与准确性。

随机选择数据量为800、2 000的数据集作为实验数据，分别采用文献[6]、文献[7]算法与所提算法进行实验，对比四种算法的数据挖掘性能，实验结果见表2。AD表示实验数据量，单位为个，用g表示；Time表示数据挖掘运行时间，单位为秒，用s表示；Ac表示数据挖掘结果的准确度，单位为%。

表2 三种算法的跟踪性能对比

分析表2数据，当数据量为800个时，3种数据跟踪算法中，文献[6]算法为21.13 s，跟踪结果的准确度为92.3%；文献[7]算法的数据跟踪时间为22.45 s，准确度为93.7%；所提算法所需时间为20.07 s，准确度为95.4%。所提算法的反馈时间最短，准确度最高，对比数据量为2 000个时的实验数据，可以验证以上结论。数据量增加时，所提算法的挖掘时间增加量与挖掘结果准确度降低量更小，由此表明，所提方法的性能更优越，且数据挖掘更稳定。

3 结 论

对数据共享效果的跟踪在各领域的应用日益广泛，针对当前数据跟踪算法存在的问题，提出基于加权关联规则的数据共享效果跟踪算法。利用模糊加权关联规则解决了原有数据挖掘算法中的数据硬分类问题，使数据划分更加合理。基于数据分类之间的关联映射关系，加入跟踪因子，得到数据跟踪算法，完成了对同一维度数据对不同维度数据的有效跟踪，仿真实验证明了该算法的数据跟踪性能，当数据量为800个时，该算法的跟踪时间为20.07 s，精度为95.4%，当数据量为2 000个时，该算法的跟踪时间为45.71 s，精度为95.1%，优于其他算法。未来阶段，将深入研究数据间的复杂关系，并研究学习相关专家、学者所提算法，进一步提高数据跟踪的效率与精准度，增强算法的适用性。