图博弈下具有未知动态的供应链系统变更设计
范佳慧,李庆奎
(北京信息科技大学 自动化学院,北京 100192)
0 引言
供应链系统是由不同节点企业如供应商、制造商、销售商等集成,涉及资金流、物料流、信息流的复杂网络系统。一般来说,不同形式的供需网络皆可视为供应链系统[1]。供应链系统是一个复杂的动态系统,动态复杂性最明显的特征是在供应链系统运行中表现出来的不确定性动态行为,包括子系统之间的切换和不确定扰动引起的需求变异放大即牛鞭效应,这种不确定性使得供应链管理更加困难[2]。
近些年随着我国经济的高速发展以及科技的日益进步,对供应链系统的稳定性分析成为各学者研究的热点[3]。文献[4]提出了一种基于过程仿真的方法,为每一次供应链内产品设计变更选择最经济的路径,以减少复杂产品开发过程中发生变更的总过程时间,并开发了基于蒙特卡罗方法的模拟算法,用于寻找可行的输出路径和计算输入变化对任务的影响。文献[5]通过考虑供应商、公司的仓库和公司生产设施中断的影响,分析了供应链系统中不同的变更案例,建立了Wagner-Whitin模型求解每种类型干扰的最优排序策略,并找到使公司预期成本最小化的订单策略。值得注意的是,目前的研究多从管理学角度,很少有学者从系统动力学角度兼顾切换拓扑结构研究供应链系统的变更设计。本文将供应链系统变更的一致性问题主要放在多智能体的动态图博弈框架中考虑,主要任务是分析供应链系统在发生变更时的状态演化机制,并保证系统的稳定状态。
博弈论为研究多智能体最优控制问题提供了一个合适的思路。在该框架下,每个智能体都试图优化自己的性能,得到最优控制策略。由于实际系统中外界干扰的存在,在博弈问题中,求解最优控制策略即需要求解耦合的Hamilton-Jacobi-Isaacs(HJI)方程。针对HJI方程直接求解困难的问题,文献[6]提出了一种基于模型的离线策略迭代算法,仅利用在线测量的状态/输出信息对某一控制策略进行评估,并找到更新后的控制策略。随着强化学习和神经网络的发展,与之结合的在线算法[7-10]逐渐受到关注。文献[11]提出了一种多智能体强化学习算法来求解耦合HJI方程,并证明了该算法收敛于最优解。文献[12]利用自适应动态规划和零和微分图博弈理论,提出在线算法,降低计算复杂度。不同于现有研究结果,本文提出一种自适应最优分布式(heuristic dynamic programming,HDP)算法,无需系统动力学知识即可求解耦合的HJI方程。
1 供应链系统建模
将供应链链主视为领导者,子供应链建模为跟随者,子链需要对链主的库存状态进行追踪并达到理想库存水平。本文考虑系统出现变更,假设变更前供应链系统稳定运行,且能与链主达到一致性,发生变更后,变更后的系统依然需要与原链主保持一致性,即达到理想库存水平。
假设非线性供应链系统由N个节点设备组成,每一个设备将自身采集的原料或生产物品提供给下一个设备。在k时刻第i个设备的库存状态和不确定需求分别用xi(k)∈ni和ωi(k)∈qi(i=1,2,…,N)表示。对末端设备而言,由于其与市场直接进行交互会受到不确定需求ωi(k)的影响,当末端设备不能抑制市场需求带来的波动时,会产生牛鞭效应。根据供应链系统上各节点设备之间的物料传输关系,将非线性供应链中第i个设备的动力学方程建模为
xi(k+1)=fi(xi(k))+gi(xi(k))ui(k)+
hi(xi(k))ωi(k)
(1)
式中xi=[x1,x2,…,xi]T∈ni为库存状态矢量;ui(k)∈mi为系统的控制输入,控制输入不但代表了第i个设备的生产率,也包含了对上一设备产品部件产出数量的需求;fi(xi)∈ni,gi(xi)∈ni×mi和hi(xi)∈ni×qi分别是第i个子链未知的状态、输入和扰动动力学形式;从实际情况出发,本文考虑异构多智能体系统,即供应链的每个子链的动力学是不同的,ωi(k)∈L2[0,∞)为不确定需求,视为外界干扰。
考虑供应链系统存在一个链主,子供应链需要根据链主和邻居供应链的库存状态变化调整其自身库存状态,假设链主的动力学方程为
x0(k+1)=f0(x0(k))
(2)
式中x0(k)∈n0。将式(1)和式(2)结合,得到如下基于多智能体的非线性供应链系统:
(3)
假设1非线性供应链系统中第i个设备的最大库存水平是ci且非线性供应链系统上的每个设备的库存状态都满足
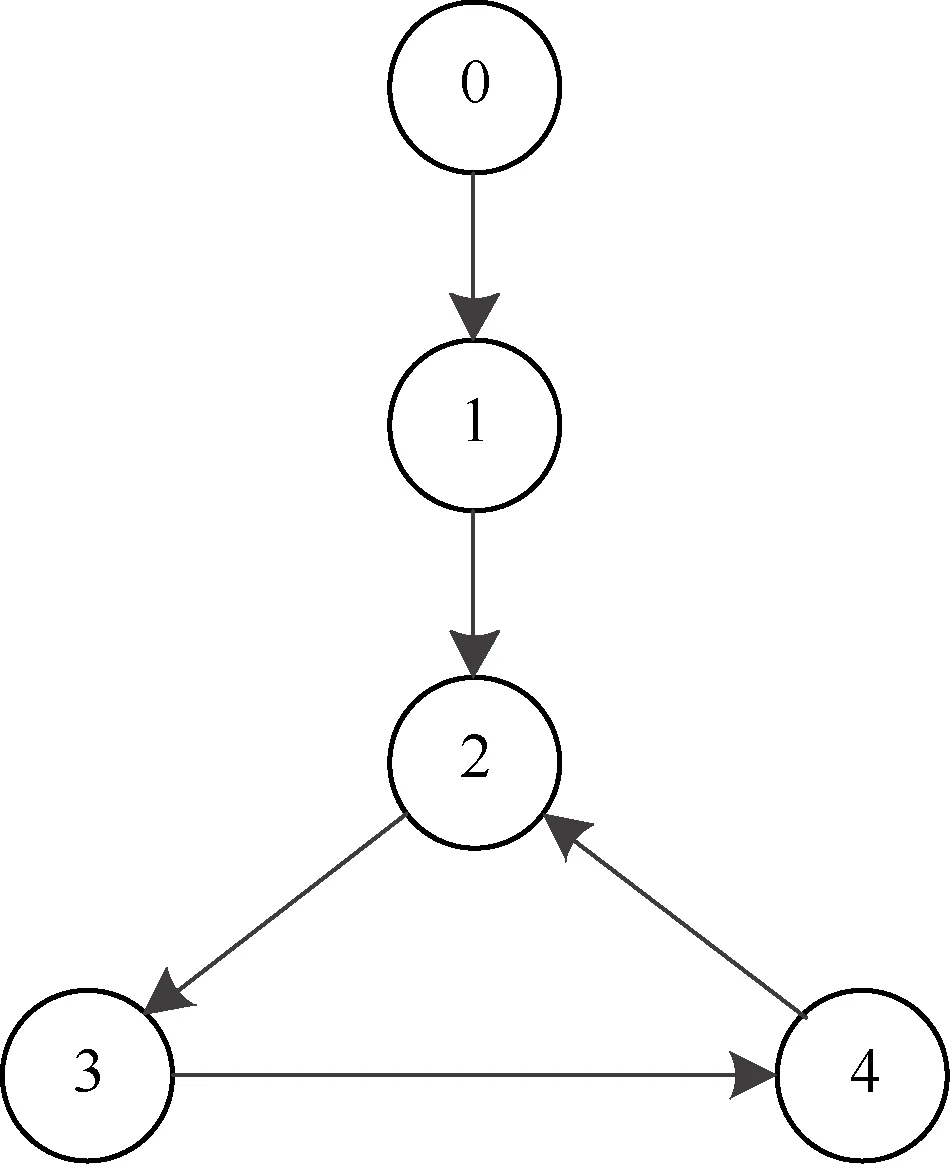
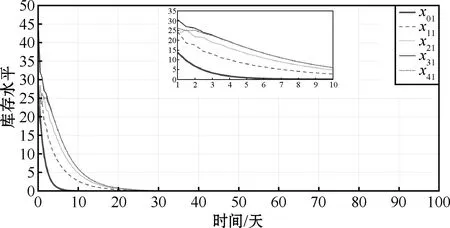
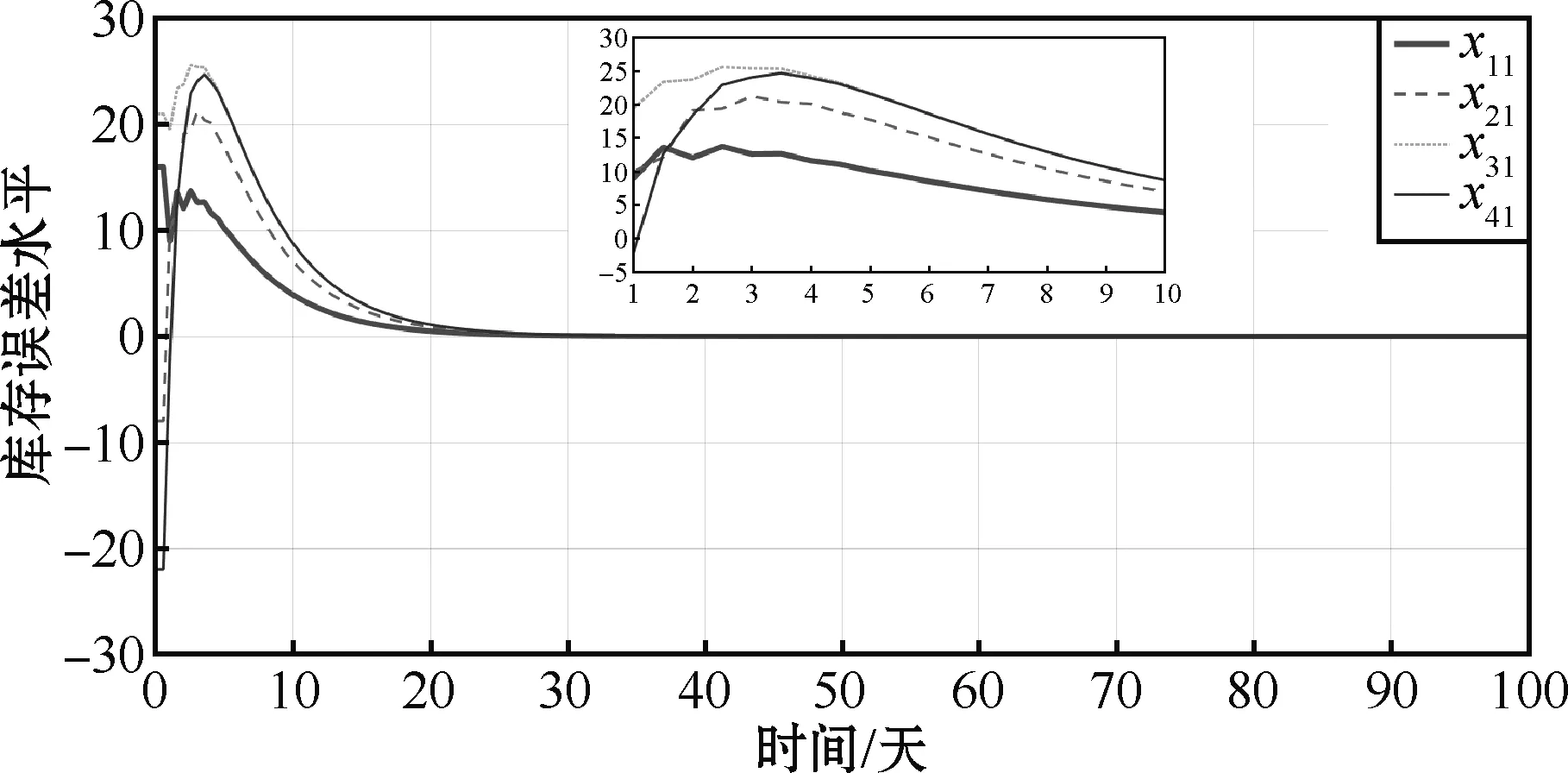
0 定义每条子供应链的局部库存误差εi(k)∈ni: (4) ε(k)=-((L+B)⊗In)η(k) (5) 式中B代表牵引矩阵,它表明链主与各个子供应链的拓扑连接情况,且有B=diag(bi)N×N。根据同步库存误差的定义可得供应链系统同步库存误差的全局动力学方程: ε(k)=-((L+B)⊗In)x(k)+ (6) 引理1如果L+B是非奇异矩阵,则同步库存误差向量满足: (7) 式中σmin(·)为矩阵的最小奇异值。为了简单起见,xi(k)从现在起写成xik。 注1假设供应链系统拓扑结构中存在生成树,并且任一子链的bi≠0,则L+B非奇异。 根据式(3)和式(4),供应链系统第i个子链的局部邻域跟踪误差的动力学方程为 (8) 神经网络用于识别供应链子系统式(1)的未知动态。根据神经网络的通用逼近特性,可以将子系统式(1)近似为 (9) 式中:φi(·)为激活函数;εis(k)为神经网络估计误差;zi(·)为神经网络的输入;vis和Wis分别表示输入层和隐藏层、隐藏层和输出层之间的理想权重矩阵。 系统辨识的近似误差可定义为 (10) 平方近似误差定义如下: (11) 采用梯度下降规则用于最小化式(11)并更新神经网络权重: (12) 存在链主时的供应链系统跟踪一致问题可通过零和博弈方法进行分析求解,首先针对供应链同步库存误差系统式(8)定义一个性能指标函数: Ji=({εik,uik,u-ik,ωik,ω-ik}k≥0)= (13) 式中:Qii>0∈ni×ni;Pii>0∈qi×qi;Pij>0∈qj×qj;W(·)>0;γ>0为一个给定的常数;u-i={uj:j∈Ni}和ω-i={ωj:j∈Ni}分别是相邻子链的控制输入和干扰。为考虑控制输入约束,每个子链使用如下非二次泛函如下: (14) 式中:R>0为正定对角阵;π∈mi;φ(·)∈mi;φ-1(ui)=[φ-1(ui(1))φ-1(ui(2))…φ-1(ui(m)]T;φ(·)为单调奇有界函数,满足|φ(·)|≤1,且其一阶导数是有界的;是执行器的界。 生产率的目标是最小化性能指标函数,而不确定市场需求的目标是最大化性能指标函数。 当ωi(k)=0时,解决零和动态图博弈的同步问题即要找到一个约束控制输入ui(k),当ωi(k)≠0时,对于给定的γ>γ*,应满足如下有界L2增益条件: (15) 式中:β为有界函数,且β(0)=0;γ*为满足上述有界L2增益条件的最小γ值。 定义1对于系统输入uik,∀i可以稳定系统式(8),并保证相应的值函数是有限的,则i被定义为可容许的。 给定供应链系统的容许控制策略,每个子系统i的值函数定义为 (16) 由式(16),每个子链的Bellman方程为 Vi(εik)=Ui(εik,uik,u-ik,ωik,ω-ik)+ Vi(εi(k+1)) (17) 式中初始条件Vi(0)=0。 (18) 式中:u-i={uj:j∈Ni};ω-i={ωj:j∈Ni}。 因此,每个子链的有界最优控制策略和最坏扰动如下: (19) (20) (21) 基于误差动力学式(8)和性能指标式(13),每个子链i的哈密顿函数定义为: bi(f0(x0)-fi(xik))-(dj+bj)(gi(xik)uik+ (22) ω-ik))= (23) (24) 将式(23)和式(24)代入式(22),得到以下的耦合DTHJI方程: (25) 式中,初始条件Vi(0)=0。耦合Bellman最优方程式(21)和DTHJI方程式(25)是等价的[14]。求解耦合的DTHJI方程很困难。因此,采用值迭代算法来近似求解。 为了求解供应链系统的离散时间图博弈,需要找到耦合离散时间HJI方程的纳什均衡解。定义纳什均衡条件为: 定义2对于供应链的所有子链,N人博弈都有一个全局纳什均衡解: (26) 定理1给出了局部邻域跟踪误差渐近稳定以及供应链所有子链与链主保持一致性的条件。 定理2说明耦合HJI方程的解为博弈问题提供了纳什均衡解,并可以求解零和动态图博弈。相关证明可以参考文献[13],此处不赘述。 在这一部分中,提出了一种基于Bellman方程式(17)的在线值迭代HDP算法来求解零和动态图博弈。该算法求解耦合的Bellman最优方程式(21),得到控制策略和干扰策略的最优值。与策略迭代不同,值迭代不需要初始容许控制。具体算法步骤如下: 算法步骤:初始化:给定所有子链的任意初始控制、干扰策略和相应值。for l=0,1,…,迭代l次:1.策略评估:用以下公式求解Vl+1i:Vl+1i(εik)=Ui(εik,ulik,ul-ik,ωlik,ωl-ik)+Vli(εi(k+1))(27)2.策略改进:通过以下方程式更新控制和干扰策略:ul+1ik= Uφ( UR)-1(di+bi)gTiΔVi(εi(k+1))l+1(28)ωl+1ik=-1γ2(di+bi)P-1iihTiΔVi(εi(k+1))l+1(29)until满足Vl+1i(εik)-Vli(εik)≤εEnd (30) (31) (32) 执行神经网络对控制输入的逼近误差可以定义为 (33) 控制输入uik为 (34) 由式(32),式(34)可以写成 (35) 式中,Oi=2×[0…[i]ii…0]∈ni×niNij。 控制输入的执行神经网络的平方逼近误差定义如下: (36) 采用梯度下降规则来更新控制输入的执行神经网络权重: (37) 类似地,执行神经网络对扰动的逼近误差可以定义为 (38) 扰动ωik可以由评价神经网络定义为 (39) 由式(44),式(51)可以写为 (40) 为了更新扰动的执行神经网络权重,采用如下梯度下降规则: (41) 目标值函数Vik由下式给出: (42) 采用梯度下降法来更新评价神经网络的权重: (43) 针对未知动态图博弈中的执行—评价神经网络权重在线调整问题,提出了算法2,该算法仅使用系统轨迹的可测量数据。具体算法步骤如下: 算法步骤:初始化:随机初始化执行神经网络辨识器权重,并将评价神经网络权重设为零。for l=0,1,…,迭代l次: 1.计算系统轨迹上的局部跟踪误差εi0。 2.通过式(30)和式(31)计算控制策略u^lik和扰动策略ω^lik。 3.通过式(10)计算估计状态x^li(k+1)。 4.使用估计的状态计算局部跟踪误差εli(k+1)。 5.通过式(32)计算值函数V^li(k+1)。 6.更新评价神经网络权重 W^(1+l)Tic=W^lTic-μ^ic(Vik-ZTikW^lTicZik)ZikZTik式中Vik由式(42)给出。 7.更新执行神经网络权重 W^(1+l)Tia=W^lTia-μ^ia(W^lTiaZik-ulik)ZTik、 W^(1+l)Tid=W^lTid-μ^id(W^lTidZik-ulik)ZTik。 8.更新辨识器权重 W^(1+l)Tis=W^lTis-μ^isφi(W^lTisφi-xik)T。 until满足Vl+1i(εik)-Vli(εik)≤εEnd 为了验证所提方法有效性,考虑一个包含4条子供应链、一个链主的供应链系统,其中每条子供应链包含2个设备,分别负责产品的生产环节和销售环节,4条子链和链主分别通过图1所示的通信拓扑进行信息交互。图中0表示链主,1、2、3、4表示4条子链。 图1 供应链系统的拓扑结构 每个子供应链的状态、输入和干扰矩阵如下[14]: 链主的状态为: 供应链系统变更后库存变化曲线如图2~5所示。 图2 供应链系统库存状态xi1变化曲线 图2和图3展示了变更后子供应链和供应链链主的库存状态变化,变更后供应链系统中的4条子供应链在第25天左右实现与供应链链主的库存状态一致。图4和图5展示了变更后各个子供应链与供应链链主之间的库存误差变化,库存误差值在第25天左右趋于0,这也表示子链与链主之间的库存状态趋于一致,即变更后的系统仍能稳定运行。 图3 供应链系统库存状态xi2变化曲线 图4 供应链系统库存误差ηi1变化曲线 图5 供应链系统库存误差ηi2变化曲线 本文研究了零和图博弈下具有未知动态的供应链系统变更一致性问题,针对存在外部扰动的供应链变更系统,提出了一种新的自适应分布式优化算法,求解存在未知动力学的系统耦合HJI方程。神经网络用于辨识供应链系统每个子链的未知动态,并采用执行—评价神经网络逼近最优值函数、最优控制和最坏情况下的干扰策略。仿真结果表明,所提方法可以保证供应链变更系统的稳定性与一致性。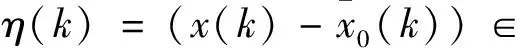
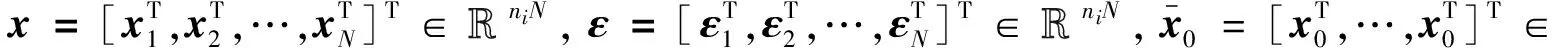

2 未知非线性动力系统的辨识
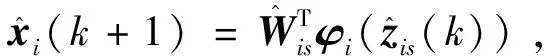
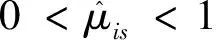
3 供应链系统零和动态图博弈
3.1 零和图博弈
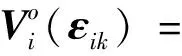
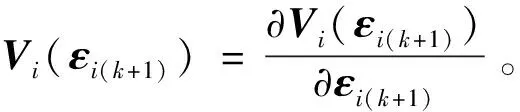
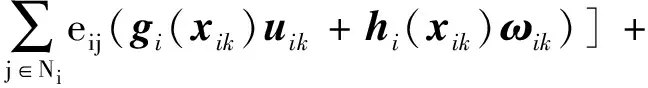
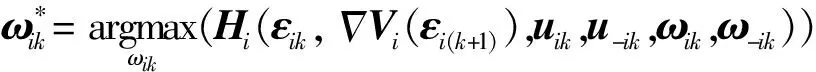
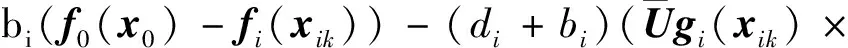
3.2 纳什均衡
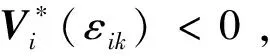
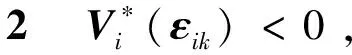
3.3 值迭代算法

3.4 求解未知动态图博弈对策值迭代HDP算法
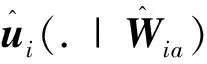
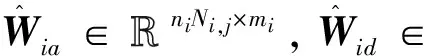

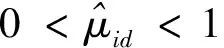
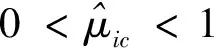

4 仿真分析
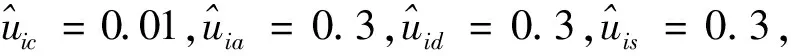


5 结束语

