考虑随机扰动的高速铁路弓网系统滑模控制研究

刘 涛 鲁小兵 张佳怡

考虑随机扰动的高速铁路弓网系统滑模控制研究

刘 涛 鲁小兵 张佳怡

（中铁二院工程集团有限责任公司，成都 610031）

受电弓与接触网的滑动接触是目前高速铁路电力机车的主要取流方式。为保证受电弓-接触网（弓网）系统的接触稳定性，对高速受电弓实施有效的主动控制是提高弓网受流质量的一种潜在措施。本文建立具有刚度、质量参数时变特征的非线性接触网模型，以准确模拟高速列车运行过程中的随机扰动。在模型基础上，采用滑模控制算法进行高速受电弓的主动控制，并引入扰动补偿策略以降低弓网接触力在随机扰动影响下的波动程度。仿真结果显示，所提基于滑模控制的高速受电弓主动控制方法可有效降低接触力波动，减少弓网离线率。

高速铁路；接触网；受电弓；滑模控制；接触力

0 引言

当前，我国高速铁路电力机车主要依赖安装在机车顶部的受电弓与架空接触网滑动接触实现持续取流，高速铁路弓网系统示意图如图1所示。受电弓与接触网的接触稳定性直接影响电力机车的供电安全：一方面，弓网接触力过大会造成受电弓滑板、接触线磨耗加剧，导致高速铁路运营成本上升，并引起安全隐患；另一方面，弓网接触力过小则会造成弓网接触不良，引起电弧击穿，产生拉弧现象，引起电力机车供电质量不稳定，严重时可导致机车供电中断。因此，研究如何保证高速铁路弓网系统接触力稳定十分必要。

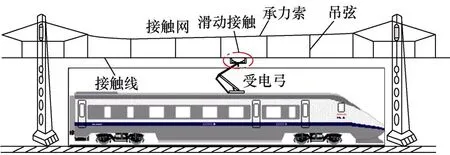
图1 高速铁路弓网系统示意图

高速铁路受电弓与接触网的结构参数不匹配是引起弓网接触力不稳定的重要原因之一[1]。因此，国内外大量学者均对优化接触网、受电弓结构参数以提高不同运行速度下的弓网系统参数匹配性，改善受流质量进行了研究[2-7]。张卫华等[8]基于弓网系统有限元模型对弓网系统参数优化对于弓网接触力的改善效果进行研究。Y. H. Cho[9]对影响弓网接触力的关键结构参数进行研究，并提出增加接触网张力以改善受流质量的方法。此外，W. Wang等[10]提出一种基于非线性阻尼器的受电弓优化设计方案，并在模型仿真中研究了此种设计方案对于受电弓动态性能的改善效果，为高速铁路弓网系统受流质量优化提供了新的思路。

除了上述高速铁路弓网系统结构参数优化研究，受电弓主动控制也是改善高速铁路弓网系统受流质量的一种重要措施[11]。受电弓主动控制是指基于现代控制理论，结合自动化技术对受电弓实施外加激励，从而有效降低弓网接触力的波动幅度，保证弓网之间的持续、良好的接触。其中，控制算法的选择直接决定了受电弓主动控制效果的优劣[12]。目前，高速受电弓主动控制主要通过对安装在受电弓底部的作动器进行调节以实现对滑板处接触力的控制，高速受电弓主动控制示意图如图2所示。由于高速铁路受电弓是一种复杂的开放式机械结构，因此在实际运行过程中往往面临各种随机扰动的影响，如环境风[13-14]、轨道激励[15]、自身结构导致的非稳态载荷传递[16-17]等。如何有效降低随机扰动的影响，是研究高速铁路受电弓主动控制必须要面对的问题。

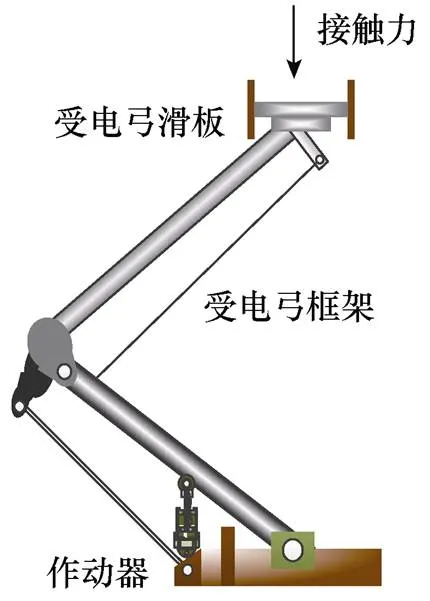
图2 高速受电弓主动控制示意图

本文为解决高速受电弓运行过程中随机扰动所造成的弓网接触力失稳问题，构建考虑随机扰动的弓网模型。在模型基础上，提出基于滑模控制理论的高速受电弓主动控制策略，并结合离散扰动控制器降低随机扰动对弓网接触力的影响。所提控制策略可有效降低高速铁路弓网接触力的波动幅度和离线率，对于保障动车组供电安全具有十分积极的作用。

1 高速铁路非线性弓网模型

模型仿真是当前应用最为广泛的高速铁路弓网系统动态行为研究方法，本节采用有限元方法建立高速铁路接触网非线性模型和高速受电弓二元归算质量模型，并采用罚函数法实现受电弓与接触网之间的动态耦合。

1.1 接触网非线性有限元模型

高速铁路接触网系统主要由接触线、承力索、吊弦和定位支撑装置组成，既是牵引供电网的电流通道，同时也是受电弓的机械滑道，具有大跨度、高柔性特征。同时由于吊弦的非线性收缩行为，接触网具有较强的非线性特征。本文采用柔性索单元、非线性杆单元建立接触网模型[18]，以反映接触网的非线性变形，高速铁路接触网有限元模型单元如图3所示。

图3 高速铁路接触网有限元模型单元

1.2 受电弓模型

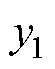
式中，即为弓网离线。

1.3 弓网模型验证

本文采用欧标EN 50318[19]对所建立高速铁路弓网模型的有效性进行验证，结果见表1。由表1数据可知，本文所建立高速铁路弓网模型符合相关标准要求，可用于高速铁路弓网系统动态行为研究。

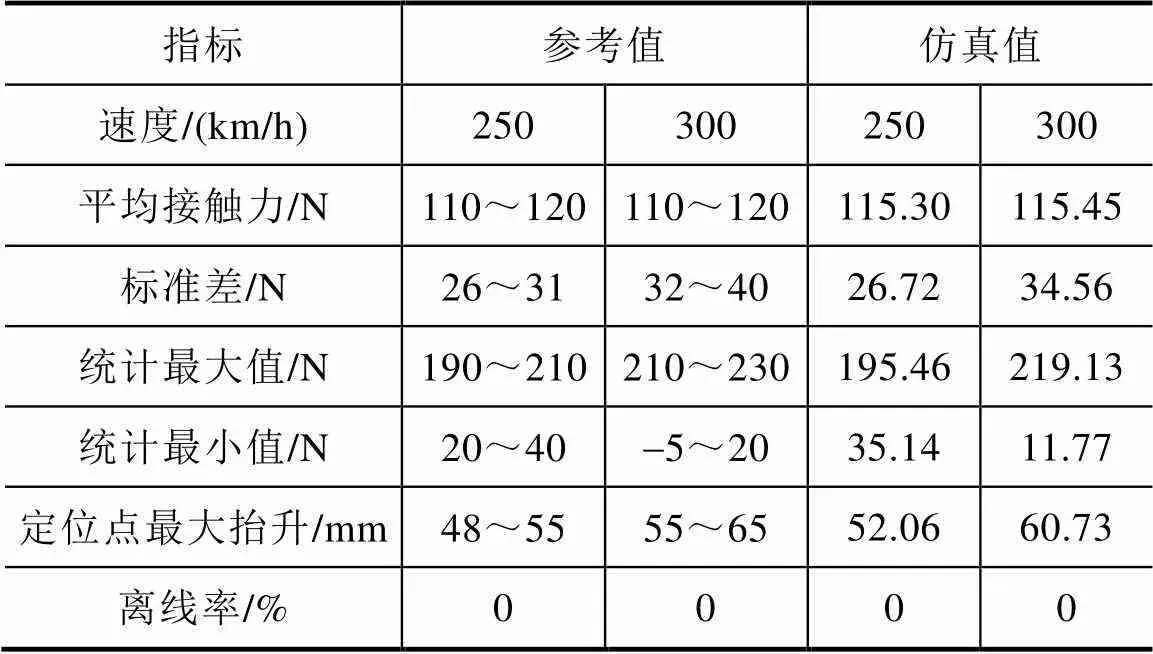
表1 模型验证结果（EN 50318）

2 高速受电弓滑模控制器设计

由于高速铁路接触网系统非线性较强，在设计高速受电弓主动控制器时，无法直接采用上文所建立的弓网系统有限元模型进行受电弓滑模控制器设计[20-21]，需对模型进行简化处理以满足控制器的设计需求[22-23]。

2.1 考虑随机扰动的接触网时变参数模型

随机扰动是高速铁路弓网系统运行过程中所必须考虑的因素，对于图5所示简化的弓网系统，其

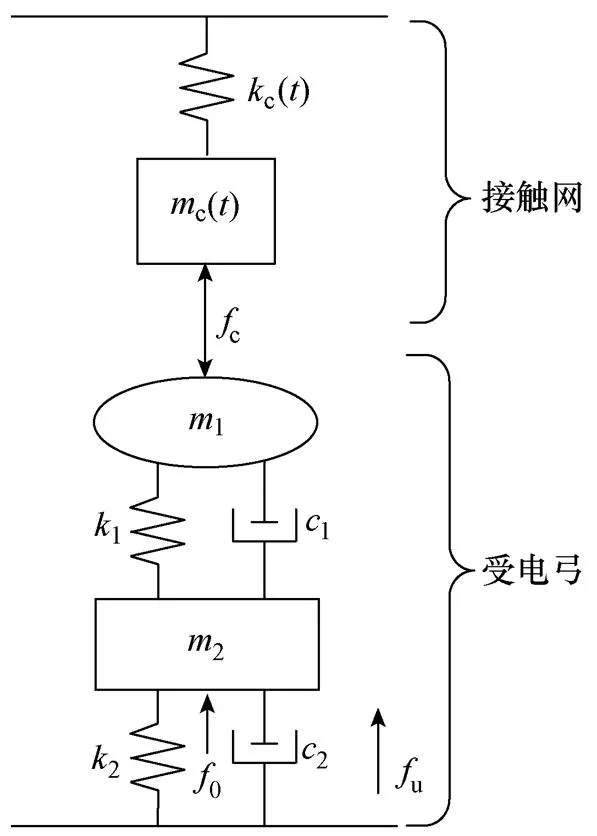
图5 高速铁路接触网参数时变模型

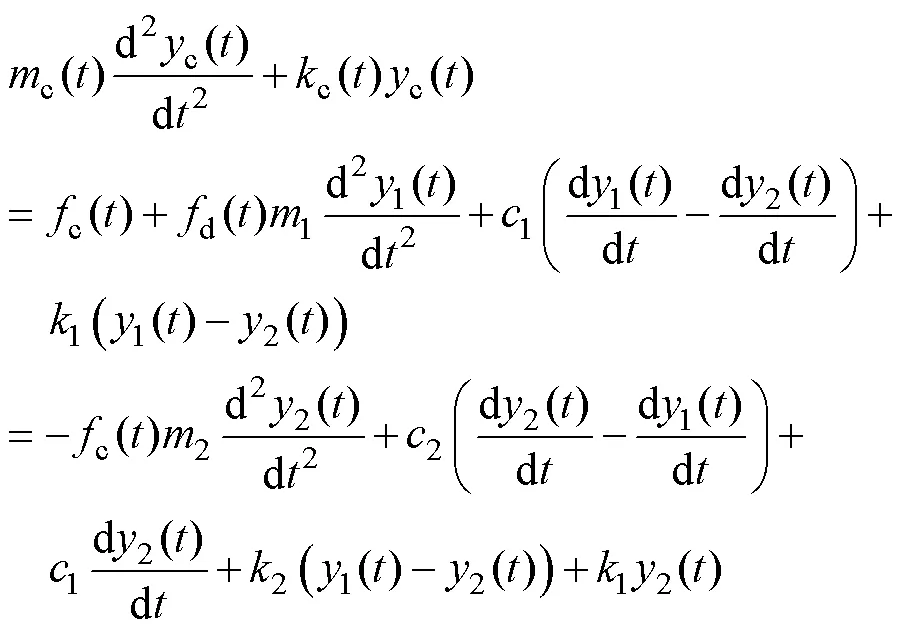
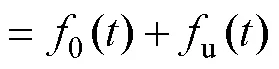
2.2 高速受电弓滑模控制器设计

在弓网系统实际运行过程中，仅有接触力、受电弓弓头、框架位移可被直接测量。根据式（1），弓网接触位置处的接触线位移可表示为接触力、弓头位移相关的因变量，即

将式（3）两侧对时间变量求导可得

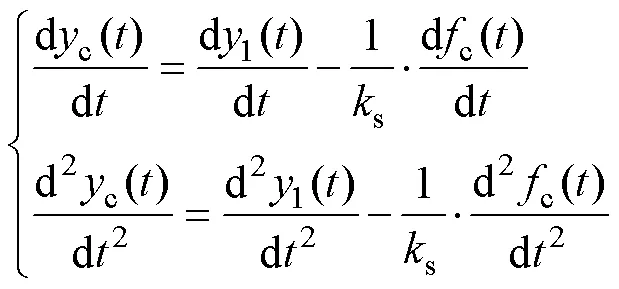
将式（3）、式（4）代入式（2），即可得到无接触线位移的弓网系统动力学归一化方程为

式中：

式（5）的状态空间方程可表示为

式中：

将式（6）所示弓网系统的连续状态空间方程进行离散化处理，即

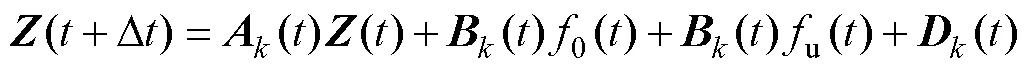
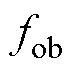
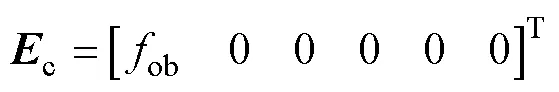
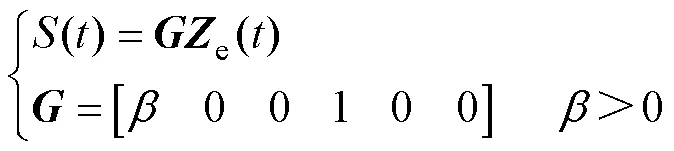
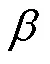
为了保证控制效果，本文在高速受电弓滑模控制器中引入持续控制策略，其离散化形式可表示为

式中，为高速受电弓滑模控制器的趋近律因子。一般地，值越大，则滑模控制器的响应越快，但其波动会更加剧烈。因此，可根据主动控制稳定性原则对的取值进行确定，即

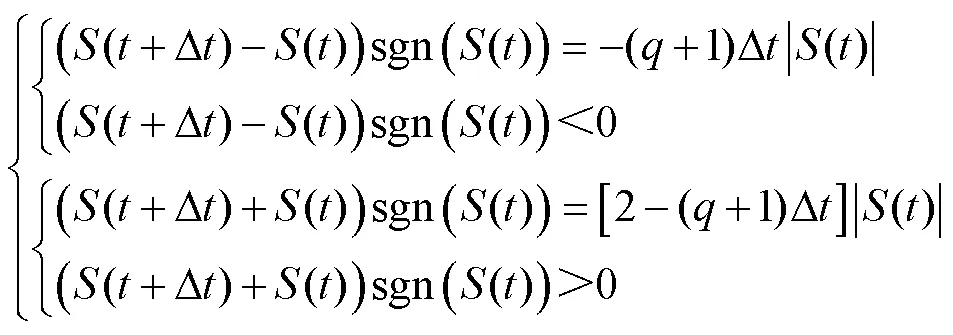
式中：

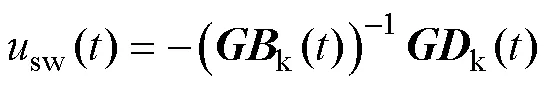
2.3 高速受电弓主动控制扰动补偿器设计

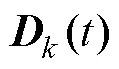
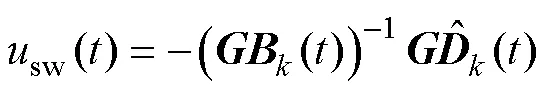
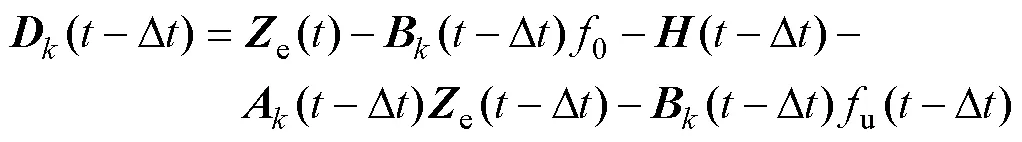
则时刻弓网扰动量估计值可表示为

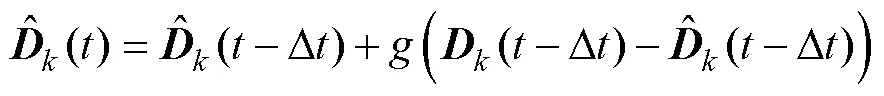
且

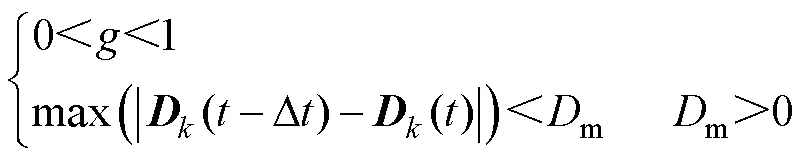
2.4 高速受电弓滑模控制器控制力修正

3 高速受电弓滑模控制效果评估

本文采用模型仿真手段对所设计高速受电弓滑模控制器的应用效果进行评估，包括考虑接触网非线性特征的模型验证与考虑接触线不平顺的受电弓主动控制效果验证。

3.1 考虑接触网非线性的高速受电弓主动控制效果

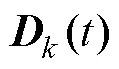
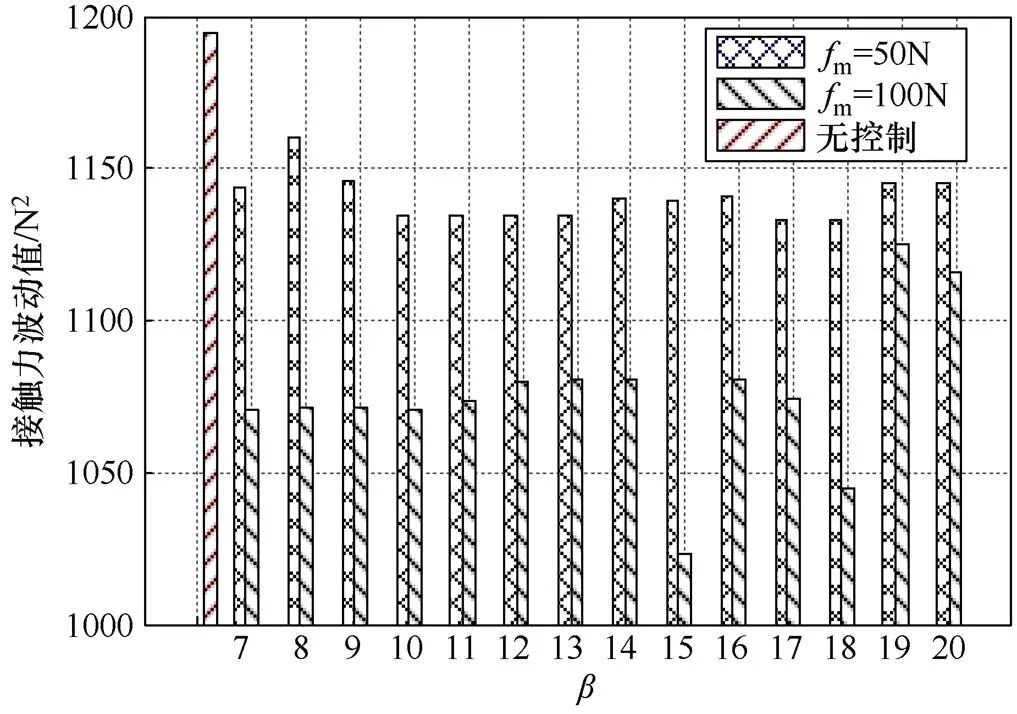
图6 高速受电弓滑模控制效果

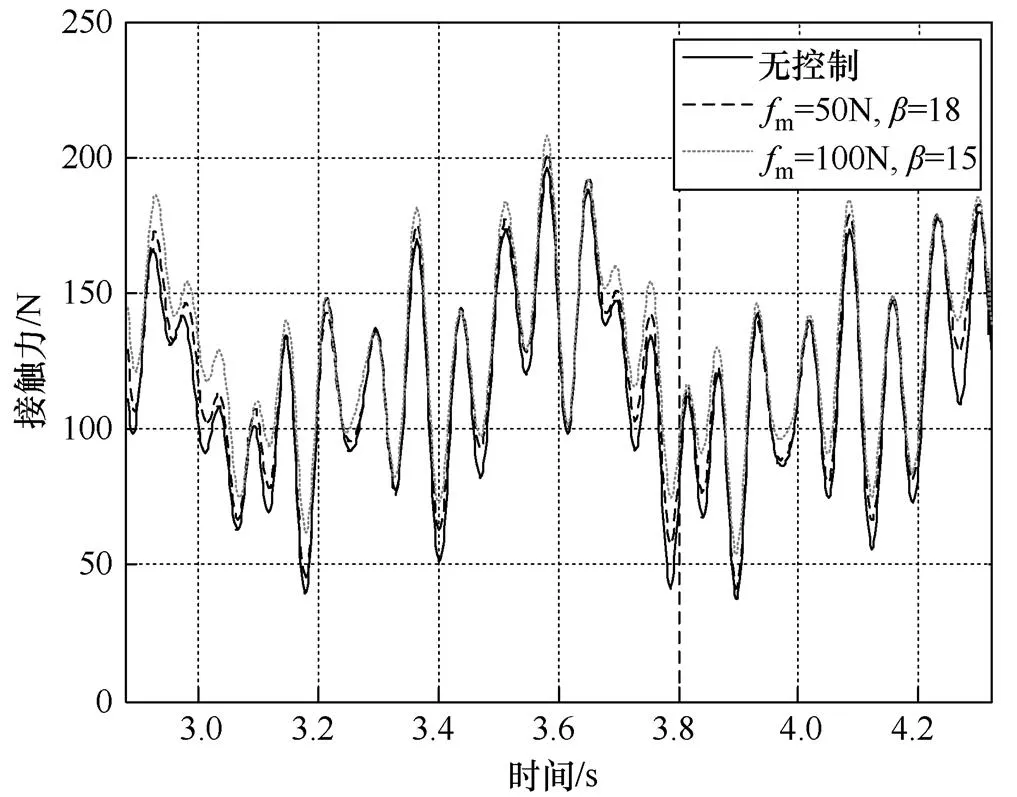
图7 弓网接触力对比

3.2 考虑接触线不平顺的高速受电弓主动控制效果

接触线不平顺是高速铁路受电弓运行过程中随机扰动产生的重要原因之一。对于高速铁路接触网，接触线不平顺可表示为

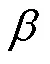
表2为不同接触线不平顺波幅下的高速受电弓主动控制效果。由表2数据可知，尽管随着接触线不平顺波幅的增大，弓网接触力波动值、离线率均逐渐增加，但本文所设计高速受电弓滑模控制器较无控制工况仍可降低弓网接触力波动值，并显著降低离线率。

4 结论

本文针对高速铁路运行过程中受电弓受到随机扰动影响引起弓网接触失稳的现象，提出了采用考虑随机扰动的滑模控制策略对高速受电弓进行主动控制，以保证受电弓与接触网之间的稳定接触。仿真结果显示，本文所提出的考虑随机扰动的高速受电弓主动控制器可在不同工况下取得较好的弓网控制效果，特别是在考虑高斯白噪声与接触线不平顺所造成的受电弓随机扰动时，弓网接触力均可保持较小的波动与较低的离线率，对于保障高速铁路动车组供电安全与稳定具有十分重要的作用。

[1] 张宗芳, 刘文正, 张坚, 等. 基于响应面法的高速铁路接触网参数优化研究[J]. 铁道标准设计, 2019, 63(9): 130-137.

[2] XU Zhao, SONG Yang, LIU Zhigang. Effective measures to improve current collection quality for double pantographs and catenary based on wave propagation analysis[J]. IEEE Transactions on Vehicular Technology, 2020, 69(6): 6299-6309.

[3] 关金发, 田志军, 吴积钦. 受电弓与接触网系统方案设计方法及其应用[J]. 铁道标准设计, 2020, 64(2): 162-167.

[4] 唐周林. 基于正交试验法的高铁弓网动态性能优化研究[D]. 成都: 西南交通大学, 2017.

[5] ZHANG Jian, LIU Wenzheng, LIU Zongfang. Sensitivity analysis and research on optimization methods of design parameters of hig-speed railway catenary[J]. IET Electrical Systems in Transportation, 2019, 9(3): 150-156.

[6] 刘方林. 不同张力等级下电气化铁路弓网电能传输特性研究[J]. 电气技术, 2017, 18(12): 86-89.

[7] CHU Wenping, SONG Yang, DUAN Fuchuan, et al. Development of steady arm damper for electrified railway overhead contact line with double pantographs based on numerical and experimental analysis[J]. IET Electrical Systems in Transportation, 2021, 11(3): 269-277.

[8] ZHOU Ning, ZHANG Weihua. Investigation on dynamic performance and parameter optimization design of pantograph and catenary system[J]. Finite Elements in Analysis and Design, 2011, 47(3): 288- 295.

[9] CHO Y H. Analysis of the major design parameters of a pantograph-railway catenary system for improving the current collection quality[J]. Journal of the Korean Society for Railway, 2014, 17(1): 7-13.

[10] WANG Wenlin, LIANG Yuwen, ZHANG Weihua, et al. Effect of the nonlinear displacement-dependent characteristics of a hydraulic damper on high-speed rail pantograph dynamics[J]. Nonlinear Dynamics, 2019, 95(4): 3439-3464.

[11] 罗维, 陈明国, 刘海波. 中国标准动车组受电弓主动控制单元设计[J]. 电力机车与城轨车辆, 2019(2): 42-44.

[12] 鲁小兵, 刘志刚, 宋洋, 等. 受电弓主动控制综述[J]. 交通运输工程学报, 2014(2): 53-65.

[13] 赵萌, 刘晓禹, 贾彦, 等. 横风作用下高速列车受电弓滑板的气动特性分析[J]. 内蒙古工业大学学报 (自然科学版), 2018, 37(5): 374-381.

[14] 牛纪强, 梁习锋, 周丹. 高速列车过车站受电弓气动冲击载荷研究[J]. 振动工程学报, 2017, 30(2): 333-340.

[15] 杨晶, 朴明伟, 高文斌, 等. 基于轮轨弓网双耦合的高速受电弓横向减振技术对策[J]. 计算机集成制造系统, 2019, 25(8): 1908-1919.

[16] 林光华, 邓磊, 王潇, 等. 受电弓升弓控制回路测试与分析[J]. 电器与能效管理技术, 2020(11): 46-51.

[17] 王江文, 梅桂明, 李瑞平, 等. 弓网相互作用时受电弓关键部件动载荷研究[J]. 铁道学报, 2018, 40(3): 68-75.

[18] 鲁小兵. 基于状态估计的高速铁路受电弓主动控制方法研究[D]. 成都: 西南交通大学, 2018.

[19] Railway applications. Current collection systems. Validation of simulation of the dynamic interaction between pantograph and overhead contact line: BS EN 50318—2018[S]. UK: BSI Standards Limited, 2018.

[20] 孙宜标, 仲原, 刘春芳. 基于LMI的直线伺服滑模位移跟踪控制[J]. 电工技术学报, 2019, 34(1): 33-40.

[21] 王江彬, 刘凌, 刘崇新. 基于扩张状态观测器七阶混沌振荡电力系统的滑模变结构控制[J]. 电工技术学报, 2020, 35(21): 4524-4531.

[22] 何亚华, 王丽梅. 基于双层交叉耦合的直驱H型平台滑模轮廓控制[J]. 电气技术, 2021, 22(8): 10-14.

[23] 杨杰, 黄晨, 石恒. 径向基函数神经网络补偿的悬浮球悬浮高度自适应滑模控制[J]. 电气技术, 2020, 21(2): 31-35.

[24] SANCHEZ-REBOLLO C, JIMENEZ-OCTAVIO J R, CARNICERO A. Active control strategy on a catenary- pantograph validated model[J]. Vehicle System Dynamics, 2013, 51(4): 554-569.

Study on the pantograph active control based on the slide mode control method considering the stochastic disturbance

LIU Tao LU Xiaobing ZHANG Jiayi

(China Railway Eryuan Engineering Group Co., Ltd, Chengdu 610031)

The sliding contact between the pantograph and the overhead catenary is the only way for the electric vehicle to collect current, which is easily influenced by the stochastic disturbances. In this paper, a catenary model with time-varying mass and stiffness is established and the pantograph is considered a 2-degree of freedom (DOF) model. And the uncertain disturbance is included to compensate the perturbations of nonlinear effect from catenary to pantograph. A sliding mode surface is properly defined to reduce the variation of contact force. In order to decrease the effect of other uncertain disturbance, a disturbance compensator is included to estimate the disturbance in each discrete time step. Several numerical examples indicate that the proposed controller can effectively reduce the contact force fluctuation, as well as eliminate the contact loss.

high-speed railway; catenary; pantograph; slide mode control; contact force

2021-09-29

2021-11-29

刘 涛（1982—），男，河南驻马店人，硕士，高级工程师，主要从事铁路电气化设计与研究工作。

中铁二院工程集团有限责任公司科研项目（KDNQ212002）