基于两体碰撞的冲击放大机理研究

闫 明， 顾西平， 金映丽， 孔祥希

(沈阳工业大学 机械工程学院，沈阳 110870)

随着导弹、火箭等武器发射速度的提升，其中使用的微电子设备的加速度负荷急剧增加[1]。以我国军事领域应用为例，火箭、导弹的引信、电子元器件在发射阶段所承受的加速度值已经超过数千g，部分元器件所承受的加速度值已高达上万g[2-3]，例如导弹在侵彻建筑物时引信所承受的加速度为103～105g[4]。为了保证产品质量，要求产品在投入市场前要进行冲击可靠性测试。现有高加速度冲击试验方法包括真实爆炸现场模拟、空气炮、各种类型的冲击试验机[5-8]、Hopkinson 压杆装置[9]等。除冲击实验机操作相对简单外，其余试验技术相对较难，不易实现多次、重复性试验。受多项技术瓶颈限制，现有冲击试验机的峰值加速度一般不大于600g[10-11]。为了满足微电子设备的冲击试验要求，就必须提高冲击试验机的加速度峰值。双质量冲击放大器(以下简称冲击放大器)作为一种辅助装置，配合冲击试验机使用，利用碰撞产生高加速度冲击，能够解决该问题。

研究表明，实现冲击放大的方法有3种：①基于频率耦合；②基于共振；③基于多体碰撞。王怀文等[12]基于频率耦合原则设计了一款冲击放大装置，使加速度放大2倍～3倍。如果需要获得更高的加速度冲击，就必须对冲击台面施加更强的冲击，过大的冲击可能会超过冲击台面和各连接件机械强度极限，对台面和连接件造成损伤，致使该类型冲击试验设备可靠性严重下降。Sisemore等[13]基于共振原则设计了一款冲击放大装置。通过调节共振梁的固有频率使其与激励频率保持一致，利用共振来实现冲击放大。研究表明，该装置只能放大中、低频段的冲击响应，所产生的加速度放大倍数最大为4倍左右，不能放大高频段的冲击。Zhang基于多体碰撞设计了一款冲击放大器，研究了在理想条件下跌落高度、放大台质量对峰值加速度的影响，未考虑碰撞过程中的能量损失。Douglas等[14]借助有限元分析软件研究了冲击放大器的结构参数和接触参数对峰值加速度的影响，并对基于多体碰撞的冲击放大理论进行了简单描述。对于碰撞问题的研究，古典碰撞理论忽略了碰撞过程中的接触时间和接触变形。假设接触力为无穷大，仅用碰撞恢复系数来表示碰撞前后的速度跳跃关系[15-16]。而动态接触理论要求把碰撞过程微观化，充分考虑碰撞过程中的接触时间，接触力和接触变形[17-19]。此外，动态接触理论不仅可以从微观角度计算碰撞力，而且不需要求解额外的代数方程(速度跳跃关系)，因此在工程领域中得到了广泛的应用[20]。动态接触理论的关键是选择合适的接触力模型，并确定模型参数的取值，其本质是从微观上描述碰撞过程，故又称作碰撞过程模拟。本文从经典碰撞理论出发，结合动态接触理论，建立了冲击放大器运动学模型，推导出了加速度、加速度放大倍数理论计算公式，研究了碰撞持续时间比、质量比、波形发生器刚度比、对加速度放大倍数的影响，最后通过试验对两体碰撞理论进行了验证。

1 结构特征

冲击放大器结构如图1所示，主要由底座、波形发生器、放大台、导向柱、横梁、弹力绳以及其他附属部件组成。作为辅助装置需要配合冲击试验机才可以发挥作用，其工作过程如图2所示。

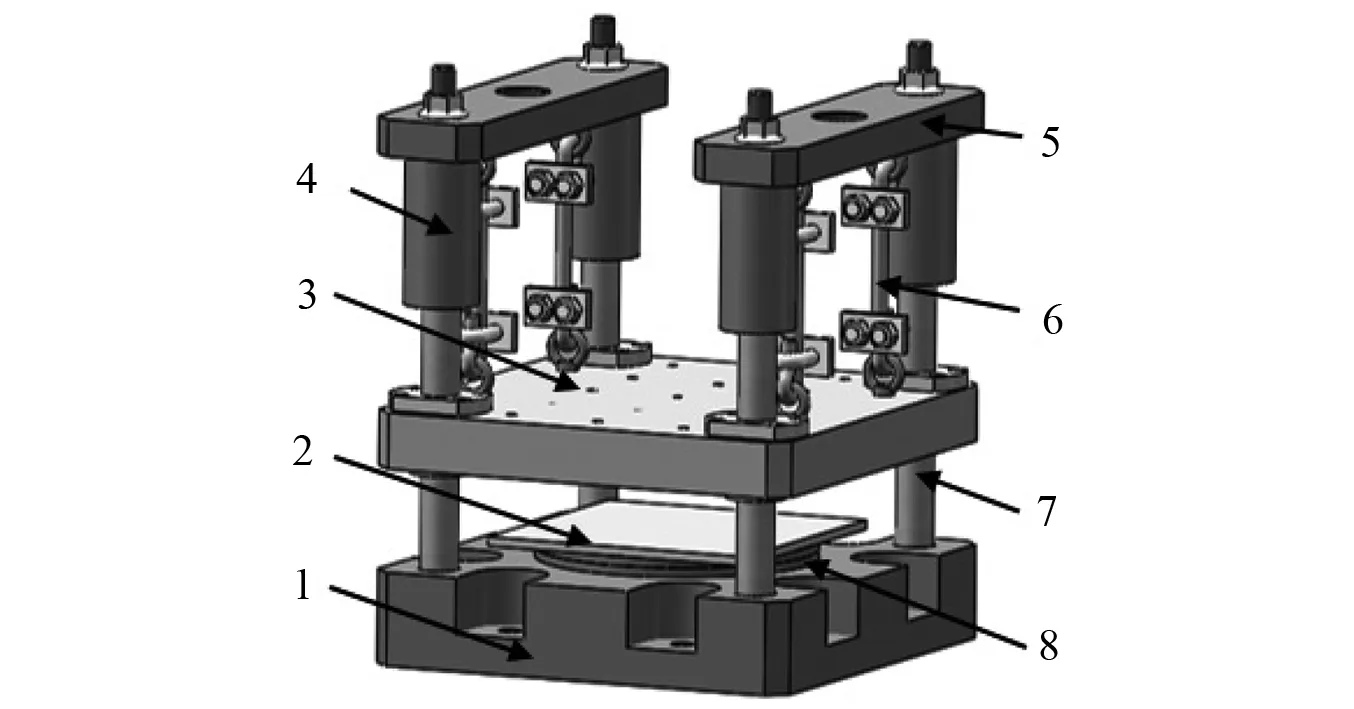
1.底座；2.波形发生器；3.放大台；4.缓冲圈；5.横梁；6.弹力绳；7.导向柱；8.间隙调整垫块。

图2 冲击放大器工作过程

冲击放大器的底座固定在跌落台上，将跌落台提升到一定高度然后释放做自由落体运动。当跌落台与基座上的波形发生器碰撞(第一次碰撞)后反弹向上运动。此时放大台由于惯性在支撑弹力绳的作用下继续向下运动，与迎面而来的跌落台发生第二次碰撞。由于放大台的质量远小于跌落台的质量，使放大台产生了很大的速度改变，又因为第二次碰撞时间极其短暂，所以就产生了比第一次碰撞高很多的加速度峰值。

2 运动学模型分析

安装有冲击放大器的跌落台从高度h处开始做自由落体运动，与基座上的波形发生器发生第一次碰撞，该过程运动学方程满足

(1)

(2)

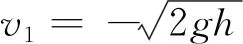
假设碰撞产生的波形为理想半正弦，则此次碰撞产生的加速度峰值满足

(3)

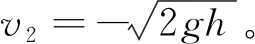
(4)

由式(4)可得

(5)

(6)

由于冲击放大器所使用的橡胶波形发生器非常薄，所产生的波形介于半正弦和三角波之间。假设碰撞产生的波形为理想三角波，该过程放大台所产生的加速度峰值可以表示为

(7)

加速度放大倍数n2满足

(8)

式中：Δt2为跌落台与放大台碰撞过程中的碰撞持续时间，由于m1≫m2，即m2/m1≈0，所以式(7)、式(8)可以简化为

(9)

(10)

由式(10)可知，当质量比满足m1≫m2时，加速度放大倍数主要有碰撞持续时间比和碰撞恢复系数决定，如图3所示。

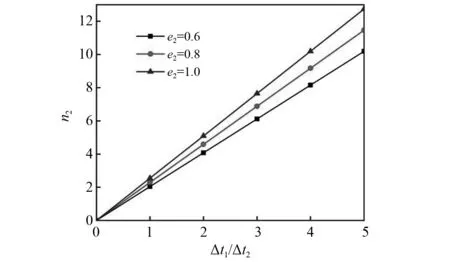
图3 碰撞持续时间比对加速度放大倍数的影响

从图3可以看出，当碰撞恢复系数一定时，随着碰撞持续时间比的增加，加速度放大倍数逐渐增加；当碰撞持续时间比一定时，随着碰撞恢复系数的增加，加速度放大倍数也随之增加。若碰撞恢复系数e2=1，加速度放大倍数趋近于8Δt1/(πΔt2)。所以增加Δt1或者是减小Δt2可以获得较高的加速度放大倍数。

由动态接触理论可知，跌落台与基座的碰撞过程可以简化为单自由度弹簧质量系统，跌落台与放大台的碰撞过程可以简化为双自由度弹簧质量系统。因此Δt1，Δt2满足

(11)

式中,k1，k2分别为基座和冲击放大器底座上橡胶波形发生器的刚度，所以

(12)

由式(12)可知，加速度放大倍数由波形发生器刚度比、碰撞恢复系数、质量比共同决定。如图4所示，研究了在碰撞恢复系数e2=1时，不同波形发生器刚度比下加速度放大倍数与质量比的关系。

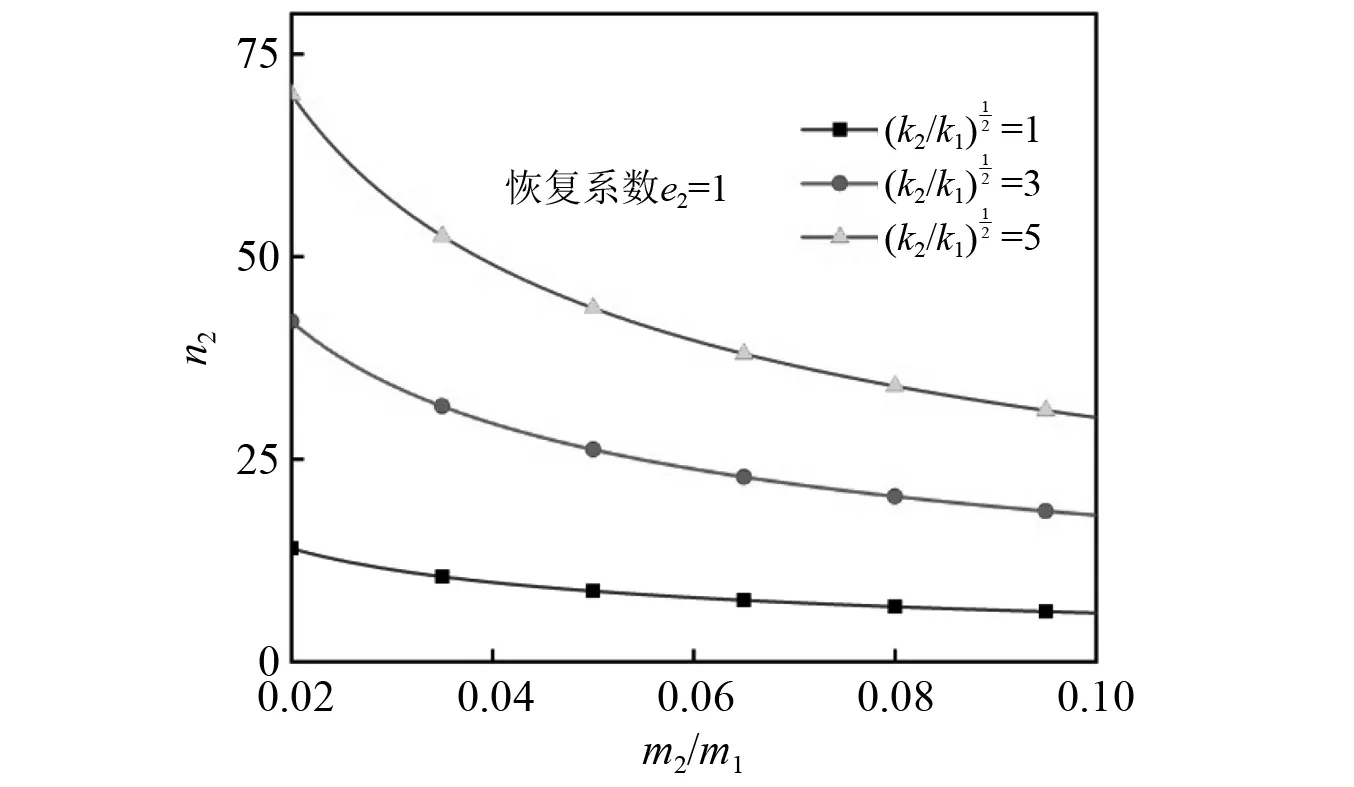
图4 不同刚度比下质量比对加速度放大倍数的影响

从图4可以看出，当波形发生器刚度比一定时，随着质量比的增加，加速度放大倍数逐渐减小，当质量比足够大时，加速度放大倍数趋近于0。为了获得更高的加速度放大倍数，可以取较小的质量比，即满足m1≫m2。当质量比一定时，随着波形发生器刚度比的增加，加速度放大倍数迅速增大，为了获得更高的加速度放大倍数，可以增大波形发生器刚度比。结合图4和式(12)可以看出，相比于减小质量比，增大波形发生器刚度比可以获得更高的加速度放大倍数。

3 两体碰撞理论试验验证

为了验证两体碰撞理论的正确性，搭建了如图5所示的冲击放大器工作平台，开展冲击试验，试验过程中跌落台与放大台加速度变化曲线如图6所示。

图5 冲击放大器工作平台

图6 h=300 mm时加速度变化曲线

试验中跌落台总质量为410 kg，放大台总质量为6 kg。由于跌落冲击试验机底座倾斜以及导杆与跌落台之间的摩擦增大，导致跌落台自由落体时加速度变小。由SY10-500跌落冲击试验系统显示面板读得跌落台自由落体时实际加速度为0.53g，然后结合试验测得e1=0.4，e2=0.72。

从图6可以看出当跌落高度为300 mm时，试验测得跌落台的加速度波形与理想半正弦波形较为接近，放大台的加速度波形与理想三角波较为接近。试验测得跌落台加速度约为78g，放大台加速度约为1 065g，加速度放大倍数约为13.63倍。

将试验测量数据与理论计算结果进行对比分析，可以得到试验测量的放大台加速度峰值与理论计算的放大台加速度峰值误差分析如表1所示。试验测量的碰撞持续时间比、质量比，波形发生器刚度比对加速度放大倍数的影响与理论计算的加速度放大倍数误差分析如表2～表4所示。

表1 加速度峰值试验与理论计算误差分析

表2 加速度放大倍数试验与理论计算误差分析

表3 加速度放大倍数试验与理论计算误差分析

表4 加速度放大倍数试验与理论计算误差分析

由表1可知，随着跌落高度的增加，加速度峰值逐渐增加，放大台加速度误差最大为7.13%，主要原因是试验产生的波形并非理想三角波形，而是一种尖峰瘦腰类波形，如图6所示，导致加速度峰值比理论计算偏大。由表2可知，随着碰撞持续时间比的增加，加速度放大倍数逐渐增加，加速度放大倍数误差最大为4.88%，试验测量与理论计算较为符合。

由表3可知，当波形发生器刚度比一定时，随着质量比的增加，加速度放大倍数逐渐减小，加速度放大倍数误差最大为4.24%，试验测量与理论计算较为符合；由表4可知，当质量比一定时，随着波形发生器刚度比的增加，加速度放大倍数迅速增加，加速度放大倍数最大为4.62%，试验测量与理论计算较为符合。

4 结 论

(1) 当碰撞恢复系数一定时，随着碰撞持续时间比的增加，加速度放大倍数逐渐增加；当碰撞持续时间比一定时，随着碰撞恢复系数的增加，加速度放大倍数也随之增加。为了获得更高的加速度放大倍数，可以取较高的碰撞恢复系数或较大的碰撞持续时间比。

(2) 当碰撞恢复系数、波形发生器刚度比一定时，随着质量比的增加，加速度放大倍数逐渐减小，当质量比足够大时，加速度放大倍数趋近于0。当碰撞恢复系数、质量比一定时，随着波形发生器刚度比的增加，加速度放大倍数迅速增加。为了获得更高的加速度放大倍数，可以选择较小的质量比或采用较高的波形发生器刚度比。

(3) 加速度放大倍数试验测量与理论计算较为符合，放大台加速度峰值误差相对较大，主要原因是实际碰撞产生的波形并非理想三角波形，而是一种尖峰瘦腰类波形，导致试验测量的加速度峰值偏大。