重采样参数优化CEEMD行星齿轮箱故障诊断方法∗

宋生建，张旭龙，申 勇

(1.新疆维吾尔自治区科技项目服务中心，新疆 乌鲁木齐 830011；2.新疆大学 机械工程学院，新疆 乌鲁木齐 830017)

0 引言

由于行星齿轮箱体积小、传动比大、承载能力强和效率高等优点，被广泛应用于直升机、风力发电等大型机械设备中[1].但行星齿轮箱工况复杂，其关键零部件如太阳轮、行星轮极易发生故障，导致大型设备停工停产.既给操控人员带来极大的安全危害，也会产生巨大的经济损失[2].所以对行星齿轮箱的运行状态进行监测和诊断，是设备高效运行的必然要求，对工作人员安全保护和经济效益提高具有重大意义.

当行星齿轮箱内部发生局部故障时，引发非平稳动态响应，同时受时变路径调制及其他部件响应耦合的影响，传感器采集到的信号既非平稳又非线性，对于这类信号常使用时频域方法进行故障分析.比较成熟的有短时傅里叶变换、Wigner-Ville分布等.但短时傅立叶变换对频率分辨率固定，Wigner-Ville分布用于多分量信号时存在严重的交叉干扰项[3].在实际使用过程中无法取得满意效果，寻找最佳分析方法一直是难点和热点.经验模态分解（EMD）是一种自适应的分解方法，将原始信号局部尺度特征分解成一组有效分量之和，以便多尺度的展现信号的本质.但EMD存在过包络、欠包络、端点效应和模态混叠现象，这些缺陷的存在将直接影响分析结果[4].为了解决模态混叠的问题，Wu和Huang[5]提出了一种集合经验模态分解（EEMD），在原始信号中添加白噪声降低模态混叠，但无法消除，并且对于添加白噪声的幅值以及集合次数这两个关键参数没有一个特定的选取标准，整个分解算法也变得更加耗时.YEH等[6]提出了一种互补集合经验模态分解（CEEMD），通过添加成对的正负白噪声，在不增加计算量的前提下消除了重构信号中的残余噪声.

CEEMD方法的提出，引起了众多学者关注，添加白噪声幅值和集合次数是两个关键的参数，对整个算法分解结果影响较大.添加白噪音是为了使极值点能够更加均匀的分布，但是其幅值又不能太大，否则将增加集成次数使得计算量变大，太小则不能达到降低模态混叠的目的.在信号当中单位长度内平均极值点个数代表着信号的频率，如果信号的频率增加，极值密度则增加，极值点也将越均匀.通过增加信号频率，即使幅值较小的噪声也能引起极值足够的变化，从而使极值点分布更加均匀.综合以上分析，本文提出重采样参数优化CEEMD行星齿轮箱故障诊断方法，仿真分析和行星齿轮箱故障试验数据结果表明，该方法能够有效提取行星齿轮箱故障特征信息.

1 CEEMD方法

CEEMD分解算法是对传统EMD、EEMD方法的进一步改进，对原始信号添加成对的正负白噪声，从而消除残留噪声、提高计算效率[7]，采集原始信号，对其添加成对正负白噪声如公式（1）.

式中:ni(t)为第i次添加的白噪声；Pi为第i次加上白噪声得到的信号；Ni为第i次减去白噪声得到的信号.对得到的信号(Pi,Ni)分别用EMD算法分解，得到有效分量：

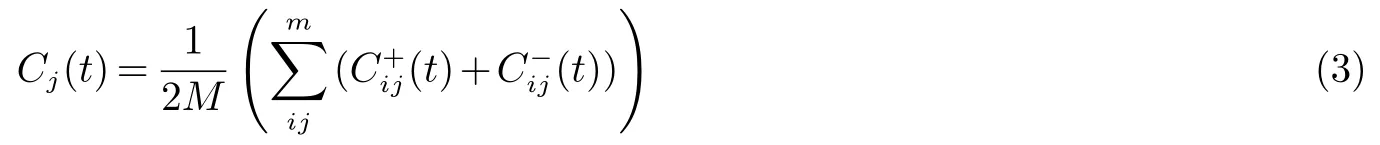
式中：Cj(t)为最终得到的第j个有效分量.

2 改进CEEMD方法

2.1 确定白噪声的幅值和集成次数

在CEEMD分解中，集成次数直接影响计算效率，因为向被处理原始信号当中添加白噪音是为了除去有效分量中残余噪声的影响[8]，所以总体平均次数必须为大于2的偶数.为了避免复杂的计算，将总体平均次数定为2最合适.根据总体平均与噪声幅值的关系A为所添加白噪声幅值；N为总体平均次数；ε为原始信号与有效分量之间的偏差).可见当偏差确定时，幅值和总体平均次数成正比.合理的选择参数将更好地消除噪声的干扰，为使分解后残留噪声的偏差小于1%，依据ε=，当N=2时，则A=0.014 SD.为使噪声残留更低，将幅值A取0.01 SD.通过如此的参数选择，信号分解效率将大大提高，并且将最大限度避免残余噪声影响.

2.2 最佳重采样频率的确定

原始信号中成份较为复杂，不仅包含行星齿轮箱系统固有耦合成份及噪音，当发生故障时响应呈现时变路径特性.采用皮尔逊相关系数表征各分量之间的线性相关性，信号经CEEMD分解后，获得有效分量IMFa和原始信号x(t)之间的相关系数如式(4)所示.

式中：Cov(IMFa,x(t))为IMFa与x(t)的协方差；V ar|IMFa|为IMFa的方差；V ar|x(t)|为x(t)的方差.

IMFa与x(t)相关系数越大，有效分量IMFa包含更多有效成份，将其作为故障特征提取对象，但IMFa中同样包含更多的干扰成份，如存在所添加白噪声的残留.已知当信号的频率增加，极值密度则增加，极值点也将越均匀，这有利于CEEMD分解消除模态混叠和噪音残留.不断插值对原始信号重采样，增加采样频率，并添加成对同采样频率的白噪声，进行CEEMD分解.随着采样频率的增加，最大相关系数将减小，但保持最大相关系数对应分量尺度不变.当相关系数最小时对应采样频率fsd（d为大于1的正整数）为最佳采样频率.通过最佳重采样频率的选择，进一步消除模态混叠，并保证故障成份不丢失.

2.3 改进CEEMD算法的提出

在改进CEEMD算法中，添加白噪声和总体平均次数振幅两个关键参数分别确定为0.01 SD和2，重采样频率根据2.2节确定，算法的流程图如1所示.

步骤一：采集故障信号x(t)，对其按2.2节方法选取最佳重采样频率.

步骤二：对故障信号x(t)进行三次样条插值按最佳采样频率重采样得到故障信号y(t).

步骤三：按2.1节确定添加白噪声幅值和总体平均次数，对其添加成对正负(+Ni(t),-Ni(t))的白噪声如式（5）所示：

式中：y(t)表示原始信号x(t)经三次样条插值后重采样信号；Ni(t)是与y(t)同频率，幅值为0.01 SD的白噪音；y1i(t)为重采样信号与白噪音相加所得信号；y2i(t)为重采样信号与白噪音相减所得信号.

步骤四：对得到的信号(y1i(t),y2i(t))分别用EMD算法分解，得到有效分量：

重复以上过程M=2次，然后对应分量组合求均值：

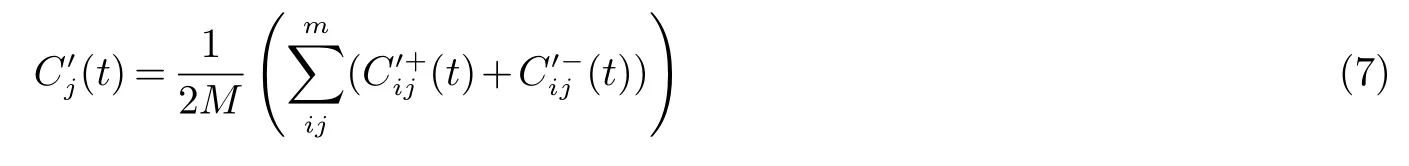
步骤五：对选取敏感的有效分量依次序抽取d个数据求和，使得分量与原始信号同长度.步骤六：对恢复原始长度的分量解调提取故障特征.

3 仿真信号验证

行星齿轮箱的正常运转有一定周期性，不同旋转部件存在高低频之分.并且啮合点产生的振动信号受到多路径的调制.当齿轮箱内部产生损伤点时将会引发高频衰减振动，并产生频率调制.所以依据以上分析建立由高频冲击信号x1、调制信号x2、高频正弦x3、低频正弦x4等4个成分构成的复杂信号x来模拟故障信号[9]：

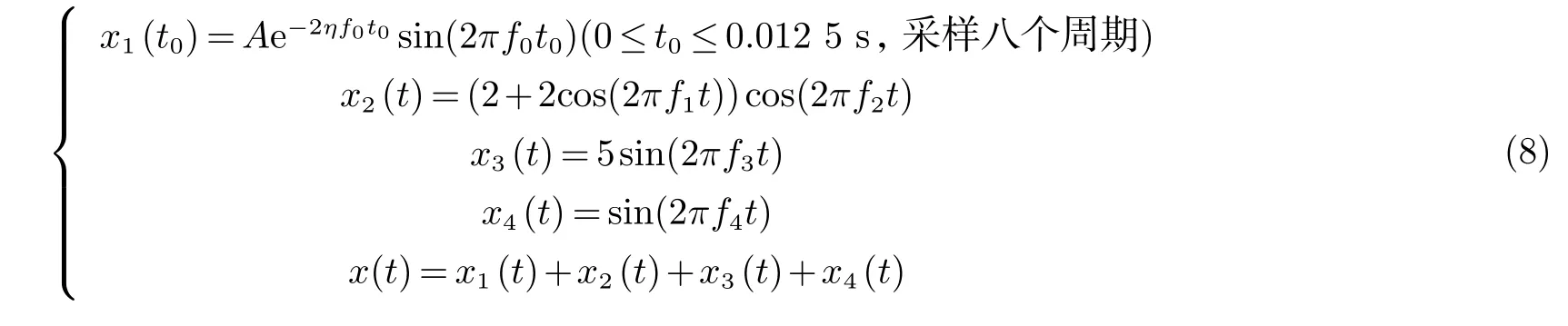
式中：η=0.04；f0=4 800 Hz；f1=150 Hz；f2=1 500 Hz；f3=500 Hz；f4=200 Hz；采样频率为fs=24 000 Hz；A=4；0≤t≤0.05 s；仿真信号及其组成部分如图2所示.

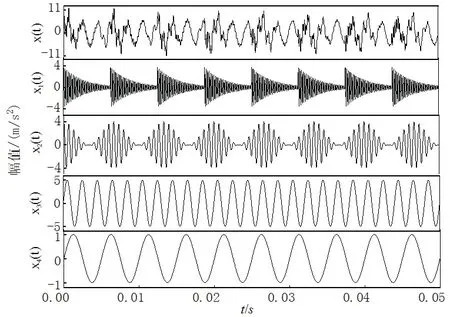
图2 仿真信号

采用本文改进CEEMD方法分解，添加白噪声的幅值为0.01 SD，总体平均次数为2.按照2.2节所提方法确定最佳重采样频率，图3（a）是随着重采样频率变化，CEEMD分解最大相关系数对应有效分量变化情况，当为原始采样频率时，最大相关系数对应分量为IMF3.选定IMF3为敏感分量，当重采样频率为3fs时，其相关系数仍为最大.若重采样频率继续增大，则最大相关系数对应分量为IMF4，按照本文选取要求确定最佳重采样频率为3fs，意在保留原始信号局部尺度特征.图3（b）是改进CEEMD分解的结果，可以清楚地看到各分量不存在噪音残留，模态混叠被消除.选取白噪声的幅值为0.01 SD，总体平均次数为200，用CEEMD方法分解结果如图3（c）所示，添加相同幅值的噪音，总体平均次数远大于2，所分解得到的有效分量存在较为严重的模态混叠现象.

图3 相关系数变化曲线及分解结果对比

通过图3（b）、图3（c）对比可知，在添加相同幅值噪音的情况下，通过重采样合理的增加信号的频率，即使在减少总体平均次数的情况下也能够有效地降低CEEMD分解所产生的模态混叠现象.作为再次对比选择EEMD，CEEMD的参数为A=0.2 SD，N=200.进行分解得到结果如图4（a）、图4（b）所示，分解结果中各分量均存在不同程度模态混叠，信号分解存在偏差.

图4 分解结果对比

为说明改进方法的有效性，对表1所示的三种分解方法进行了定量分析，通过对比分析不论是分解时间（时间由Matlab 2016b计算获得）还是分解之后各分量重构后与原始仿真函数之间的相关性，改进的CEEMD方法都更加稳妥高效.说明本文所提CEEMD的改进不仅很大程度上消除了模态混叠现象，而且信号分解更加高效精确.

表1 分解结果比较

4 实验信号验证

4.1 实验说明

为进一步验证本文所提方法对行星齿轮箱故障的有效性，用如图5所示的实验平台制造故障，采集信号进行验证.使用平台由电动机、变频器、平行轴齿轮箱、行星齿轮箱、磁粉制动器组成.通过线切割技术在行星轮的某个轮齿上沿着齿根且垂直于轮齿中心线的方向加工微小贯通裂纹作为故障，故障齿轮如图6所示.

图5 实验平台

图6 行星齿轮故障

采集信号的传感器布置在行星齿轮箱顶部，作为信号采集点.实验时，电机转速为2 100 r·min-1，设定采样频率为fs=12 800 Hz，取12 800个采样点进行分析.行星齿轮箱基本参数及计算各齿轮局部故障特征频率如表2所示.

表2 相关参数

4.2 实验数据分析

行星齿轮齿根裂纹原始故障信号时频域如图7所示.

图7 原始信号时频域图

行星轮故障振动信号及其频谱在行星齿轮故障信号频谱中，可以明显地找到其啮合频域的二倍频2fm，但其边频带多为行星架转频fc及其倍频[10]，与正常工况频谱相同，所以无法判断出故障.为了进一步分析，采用本文所提改进CEEMD方法分解，添加白噪声幅值A=0.2 SD，N=200，重采样频率按2.2节方法确定.如图8所示，当为原始采样频率时最大相关系数对应分量为IMF2.选定IMF2为敏感分量，当重采样频率为8fs时其相关系数仍为最大.若重采样频率继续增大则最大相关系数对应分量变为IMF3，按照本文选取要求确定最佳重采样频率为8fs.当重采样频率为8fs时，按照改进CEEMD分解结果如图9所示.

图8 相关系数变化曲线

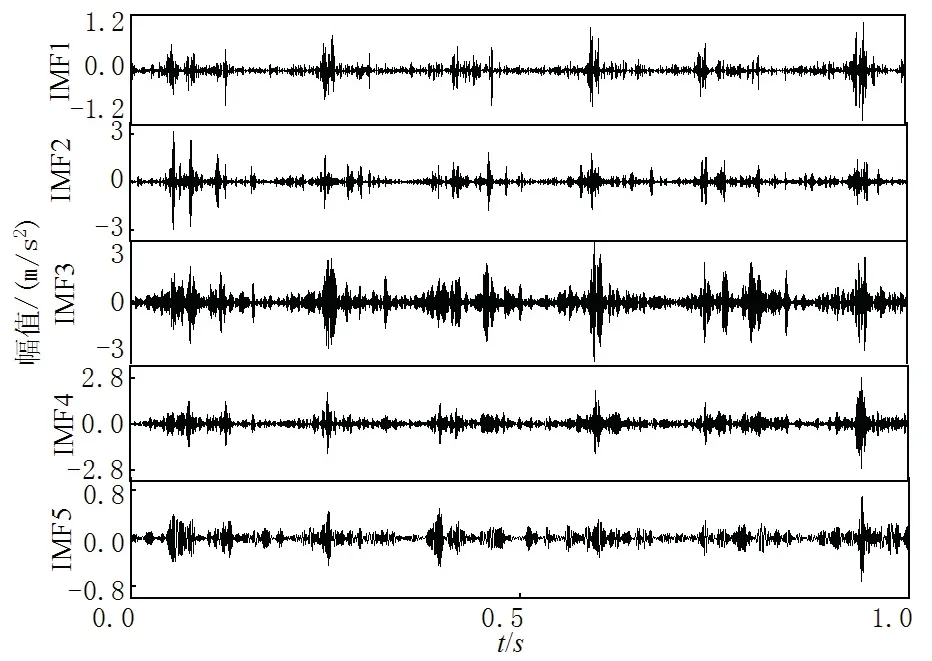
图9 改进CEEMD分解

敏感分量IMF2做进一步解调处理，幅值解调如图10(a)所示，频率解调如图10(b)所示.

图1 改进CEEMD算法流程图

在图10（a）中（红线），行星轮故障特征频率fp及其倍频nfp明显，2fp、3fp、6fp谱线凸出，其余谱线为nfp+fc，以上频谱特征完全符合行星齿轮故障特点.与改进CEEMD方法（红线）对比，CEEMD方法（黑线）敏感分量包络谱中并无有效分解出fp、3fp、4fp、6fp，并且调质成份nfp+fc较少.说明改进方法对此故障信号分解更为有效.

图10 特征提取结果

在图10（b）中（红线），行星轮故障特征频率fp及其倍频nfp明显，fp、3fp、5fp、6fp谱线凸出，其余谱线为nfp+fc，以上频谱特征完全符合行星齿轮故障特点.与改进CEEMD方法（红线）对比，CEEMD方法（黑线）敏感分量包络谱中并无有效分解出2fp、4fp、5fp，并且调质成份nfp+fc较少，说明改进方法对此故障信号分解更为有效.

5 结论

通过改进CEEMD对仿真信号与实验信号分析，可以得出以下结论：

（1）本文改进CEEMD方法比原CEEMD方法分解更加高效，分量中模态混叠基本被消除，更加适用行星齿轮故障诊断.

（2）重采样增加采样频率后，添加白噪声幅值确定为0.01 SD，总体平均次数定为2.解决了CEEMD中噪声参数选取困难、信号重构过程中残余噪声污染及运算量大的问题.

（3）改进CEEMD方法用于行星齿轮故障信号分析，更有利于故障成份的提取.对所选敏感分量进行频率解调和幅值解调，对于故障特征频率的表达更加充分，能够提取比较可靠的特征频率，成功诊断出行星轮故障.