融入平滑组稀疏化的脑部MRI图像分类

黄帅辉，王金凤

华南农业大学数学与信息学院, 广州 510642

0 引 言

阿尔茨海默症(Alzheimer’s disease，AD) (Mattson，2004)是一种由于大脑神经细胞死亡造成的不可逆的神经退行性疾病，在临床上主要体现为智能损害。针对受试者是否患病或病情程度的不同，主要分为认知正常(cognitive normal，CN)、轻度认知功能障碍(mild cognitive impairment，MCI)和AD 3种。患者在AD的治疗过程中使用的一些治疗AD的药物只能在某种程度上延缓病情的恶化。因此，实现AD早期诊断，对AD的诊断与预防都有着至关重要的作用。现阶段由于没有系统化的诊断方式，医生临床对AD诊断和后续治疗经常采用观察法，但受人为影响较大，不仅效率低下，还容易造成误判(Sakkalis，2011)。因此，智能化区分AD发展阶段是帮助临床医生预防和治疗AD的重要步骤。

核磁共振成像(magnetic resonance imaging，MRI)(Frisoni等，2010；Feng等，2021；Lee等，2019)是一种常见的生物标志物，具有无创性、可用性以及对疾病发作后大脑变化的高度敏感性,并具有高空间分辨率的脑形态可视化能力等一系列优点(Lin，2000)，是研究AD引起的各种脑结构和形态学变化的理想工具，通常用于诊断AD的标准临床评估(陈弘扬 等，2021)。MRI分为结构MRI(structural MRI, s-MRI)和功能MRI(functional MR, f-MRI),本文研究s-MRI,对MRI而言，能够获取的图像数量通常远小于图像的特征维度，并且图像中的许多特征与学习任务并不相关，即具有小样本高维度的特性。对此，如果先验知识不足，可以考虑对大脑全体结构(de Magalhães Oliveira等，2010；Liu等，2013)的特征进行分析，这种方法通过将每个结构的描述压缩成标量或低维表示，并忽略其结构内部的详细信息，从而获取关于整体的特征。此外如果可以结合一些标准的脑部模板进行配准，将每个受试者图像映射到同一标准空间中，再分别提取目标特征，将大幅提升结构内的相关性，以获取更为合理的特征分布。这些标准大脑模板通常将大脑分为若干个区域，如116个区域的自动解剖标准模板(anatomical automatic labeling，AAL)(Tzourio-Mazoyer等，2002)。

选择所有体素特征进行分类不是一个理想的选择。通过特征选择步骤(Fung和Stoeckel，2007)或稀疏诱导范数(时中荣 等，2017)降低特征数量和维度，不仅能够提高分类精度，还能产生更具临床意义的结果。

组级别上的范数针对特征进行分组，以特征组为单位进行操作，进行特征组间的稀疏和选取相关特征组。传统组稀疏正则化方法(group lasso，GL)是以组为级别的一种稀疏方法(Yuan和Lin，2006；Meier等，2008)，可以针对每个解剖组进行稀疏，排除一些冗余的组，但不能对组内特征进行稀疏，因此无法去除组内一些冗余特征。针对此问题，组L1/2稀疏正则化(group L1/2，GL1/2)(Liu等，2016)通过将GL中组内的非稀疏平方范数换成能实现稀疏效果的L1/2范数进行解决，组L1/2稀疏正则化不仅可以去除冗余的组，还可以对选取组的组内特征再次进行稀疏，从而选取更为准确的特征，以提升预测准确性。但这种方法仍有局限性，由于包含一个非平滑的绝对值函数，在数值计算中将会引起振荡，很难收敛。

本文使用平滑的组L1/2稀疏正则化(smooth groupL1/2，SGL1/2)(Li等，2018；Alemu等，2019；Fan等，2020)方法，将原先组L1/2方法中含有的非平滑的绝对值函数向平滑函数逼近，解决组L1/2方法中数值计算振荡和收敛难的缺点。在本研究中，组级别使用经过与标准模板配准过的AAL116模板的各结构区域作为分组模板，其配准流程如图1所示，然后提取每个结构区域的体素作为各自的组，在这种基础上实现对组级别上的正则化效果。本文将配准后的AAL模板分成的每个区域各当做一组，每组中含有该组中所有的体素特征。同时通过SGL1/2结合C-SVM对每组的特征进行选择和分类，将原先GL1/2方法中含有的非平滑的绝对值函数向平滑函数逼近，解决GL1/2方法中数值计算振荡和收敛难的缺点。

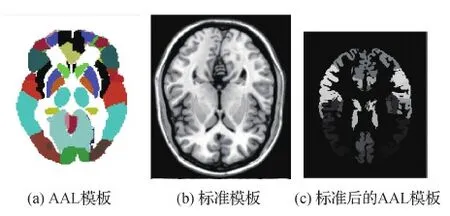
图1 AAL模板标准化过程图Fig.1 AAL template standardization process map((a) AAL template map; (b) standard template map; (c) standard AAL template map)

1 基于组稀疏方法的分类模型

本文对GL、GL1/2和SGL1/2这3种组级别上的正则化方法进行研究。

1.1 基于组稀疏化方法的特征提取

GL主要处理的是组间的稀疏关系，而对组内没有稀疏关系。GL可以用于去除一些不相关组，以达到减少数据特征维度、提升分类性能的目的。GL的函数定义为

(1)

式中，g表示第g个组，βg表示第g个组的组权重，xg表示第g个组的特征。可以看到GL可以用于对组间的稀疏，但不能对幸存组的组内特征进行稀疏。同时，它的导函数可以近似为

(2)

式中，λ是正则化参数，β是组权重，α为近似梯度的步长。

GL1/2范数有利于解决GL只能对组间进行稀疏而不能对组内特征稀疏的问题，它将GL中组间的结合方式从L1方法改变为一个L1/2方法，而组内从L2方法改变为一个L1方法。从而对组内特征能够进行稀疏选择且兼顾防止过拟合的效果。因此GL1/2既能去除冗余的特征组，又能够对幸存组的组内特征进行稀疏选择，以得到强相关组的强相关特征，最后经过分类模型训练，得到更好的分类精度。GL1/2的函数定义为

(3)

其导函数可近似为

(4)

式中，βg表示不同组之间的权重，用于权衡每个组对分类的影响, sign为符号函数。

SGL1/2范数是对GL1/2的一种平滑逼近，虽然GL1/2不仅能去除冗余的特征组，还能够对幸存组的组内特征进行稀疏选择，但它与L1/2正则化类似，其定义为

(5)

由此可见，GL1/2的缺点是涉及一个非光滑的绝对值函数，导致数值计算出现振荡，收敛分析困难。SGL1/2提出对GL1/2中非光滑的绝对值函数进行平滑逼近，使得能够更快收敛和计算平稳。SGL1/2的函数定义为

(6)

SGL1/2的导函数变为

(7)

式中，f′(xg)为f(xg)的导函数。SGL1/2提出将GL1/2中的|x|用一个平滑函数f(x)替代，其定义为

(8)

本文中特征提取均根据配准后AAL模板划分的脑区组进行提取，将获取各组的灰质密度体素作为各组的特征，如图2所示，受试者的大脑图像经过预处理后获得的灰质图像也与标准模板进行配准，以保证AAL分组模板和受试者大脑存在相同空间分布。将同样空间分布的AAL模板和受试者灰质图像进行定位，对所有受试者图像都在相同定位区域提取各脑区特征，这种方法可以很好地降低受试者个体的差异性，保证研究中提取的特征实用可靠。

图2 图像预处理和各脑区组特征提取过程图Fig.2 Image preprocessing and feature extraction of brain regions((a) original MRI map; (b) preprocessed gray matter map; (c) registered AAL template; (d) localization of AAL brain regions on gray matter map)

1.2 分类模型建立

支持向量机(support vector machine，SVM)(Cortes和Vapnik，1995)是一种通过监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面。支持向量机采用损失函数与最大边距项进行结合，通过求解最小化问题来计算最优权重wopt和偏置参数bopt，具体为

(9)

u=yi(〈w,xi〉+b)

(10)

采用基于一种校准hinge(calibrated hinge, Chinge)损失函数的SVM(calibrated SVM， C-SVM)作为终端分类器，在特征提取模块的基础上完成AD的分类识别。模型构建流程如图3所示。C-SVM采用Chinge作为损失函数，具体为

图3 主要分类流程图Fig.3 Main flow-process diagram

(11)

Chinge函数分布如图4所示。当u>0时，u越大，Chinge损失越小；当u≤0时，u越小，Chinge损失越大。因此这个校准损失函数可以给分类超平面处于预测正确的一侧更小的损失，给分类超平面处于预测错误的一侧更大的损失，它从侧面向分类平面输出更大的损失。从而确保靠近超平面的样本的预测结果倾向于分布在正确的一侧。

图4 Chinge损失函数分布图Fig.4 The distribution chart of Chinge loss function

此外，对于单纯SVM模型来说，权重是一个系数向量，其中大部分是非零项(Sun等，2018)。本研究选取的数据集是一个高维小样本数据，因此选择所有体素特征进行分类是一个不太理想的选择，特征数量过多、维度过大对程序运行有极大影响，而且对分类效果没有多大提升，甚至可能降低。因此,为了减少样本特征数量,降低运算成本，本文采用基于配准的AAL116模板作为分组模板，以大脑区域的灰质密度体素作为特征，结合SGL1/2正则化的C-SVM分类模型，这种模型的总代价函数定义为

(12)

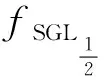
2 实现及分析

将AAL116模板作为分组模板，以大脑区域的灰质密度体素作为特征，结合SGL1/2正则化的C-SVM分类模型，对经过预处理的ADNI(Alzheimer’s disease neuroimaging initiative)数据集通过交叉验证进行训练和测试，获取测试的分类效果，并使用该分类模型对其他数据集进行重新训练与测试，对比分类效果以验证模型的泛化性能。

2.1 数据预处理

使用的数据均来自阿尔茨海默病神经成像计划(ADNI)数据集(http://adni.loni.usc.edu)。ADNI的研究对象来自美国和加拿大的50多个地点，主要目的是测试磁共振成像(MRI)、正电子发射断层扫描(positron emission tomography，PET)、其他生物标志物以及临床和神经心理学评估相结合是否可以应用于度量轻度认知损害(MCI)和早期阿尔茨海默病(AD)的识别。

实验选取ADNI中公开的ADNI1: Complete 2Yr 1.5 T的部分数据集(Wyman等，2013)，MRI图像为T1加权的1.5 T MR图像，共选择511例来自不同受试者的数据，包括AD 患者145名， MCI患者209名和正常对照(control normal，CN)组成员157名。在性别成分中，AD 男性65名，女性80名; MCI男性111名，女性98名；CN男性65名，女性92名。所选受试者详细情况如表1所示，其中MMSE表示简易精神状况检查(后同)。

表1 ADNI数据集的人员分布情况统计Table 1 Distribution of ADNI datasets

采用SPM(statistical parametric mapping)(骆姚星 等，2003)对MRI图像提取的灰质体素特征进行计算，全过程使用SPM的默认参数。

另外，本研究选取Cuingnet等人(2013)的Cuingnet数据集进行测试，以比较模型的泛化性能。在这个数据集中，509名受试者都来自ADNI，包括162例CN、137例AD、76例将在18个月内转为AD的MCI(MCIc)和134例保持稳定的MCI(MCIs)。Cuingnet数据集的特征描述如表2所示。

表2 Cuingnet数据集的人员分布情况统计Table 2 Distribution of Cuingnet dataset

由于测试的不同脑部结构大小不一，在对图像进行特征提取前需进行预处理。本研究使用SPM软件在MATLAB平台对受试者的sMRI图像数据进行标准的数据预处理操作，获得不同大脑区域的灰度体积作为训练模型的输入特征。对每个sMRI图像数据的预处理流程如图5所示。首先对图像进行AC-PC校准 (Talairach和Tournoux，1988)，AC-PC为前连合(anterior commissure，AC)后缘中点至后连合(posterior commissure，PC)前缘中点的连线，又称AC-PC线，在脑立体定位断层解剖研究中多以此线为基线。在这步操作中，先将图像的原点设置为中心，再将其注册到MNI (montreal neurological institute)空间中。之后对校正后的脑图进行去颅骨和分割处理，获取去除非脑组织的图像。然后对图像进行配准，配准使用的模板是剥离颅骨的Colin27模板(Aubert-Broche等，2006)，以获取更加清晰、高分辨率的空间模板。配准过后进行分割获取灰质图像，并对灰质图像结构进行归一化等一系列操作。

图5 图像预处理过程Fig.5 Image preprocessing process((a) original MRI map; (b) AC-PC calibration; (c) skull removal; (d) segmentation and registration)

2.2 实验设置

实验环境在单机系统搭建，处理器为Intel(R)Core(TM)i7-8750H CPU @ 2.20 GHz(2201 MHz)，32 GB内存，通过MATLAB2019a进行相关实验的运行。在实验中，将预处理过的ADNI数据集分成3个对比组，分别为AD与CN，AD与MCI以及CN与MCI。同时为了避免训练过程中的过拟合，使用K-折交叉验证法(Wu等，2010；James等，2013)，并在数值训练中选择K值为10，即10折交叉验证。采用准确度(accuracy，ACC)、接受者工作特征曲线(receiver operating characteristics curve，ROC)下的面积(area under curve，AUC)、灵敏度(sensitivity，SEN)、特异性(specificity，SPE)、精确率(precision)、召回率(recall)、几何平均值(geometric mean, Gmean)和F1分数(F1-score)等指标对分类性能进行评价。在实际AD分类中一般会出现4种情况：若一个样本是AD类(以下称为正类)且预测为正类，即为真正类(true positive, TP)；若一个实例是非AD类(以下称为负类)但预测为负类，即为假负类(false negative, FN)；若一个实例是负类但预测为正类，即为假正类(false positive, FP)；若一个实例是负类且预测为负类，即为真负类(true negative, TN)。根据这4种分类，使用的评价指标的具体定义为

(13)

(14)

式中，∑ranki表示所有正样本的序号值之和。

(15)

(16)

(17)

(18)

(19)

2.3 实施及结果分析

首先验证SVM算法采用不同损失函数对数据分类性能的影响，以获取对数据集分类效果较好的模型；之后对比在组级别上的GL、GL1/2范数和SGL1/2范数结合稀疏范数选择特征的分布和分类性能的效果；而后使用结合SGL1/2范数的校准支持向量机(C-SVM)模型，对更困难的对照组进行分类，并获取其分类效果；最后对Cuingnet数据集进行测试。

2.3.1 校准铰链损失函数对分类模型的性能影响

选取线性损失函数、逻辑损失函数、hinge损失函数和Chinge损失函数进行对比，验证基于不同损失函数的SVM 模型对测试数据的分类性能。在数据集中对AD与CN对照组进行比较，结果详见表3。可以看出，Chinge函数比其他损失函数具有更好的分类效果。C-SVM的准确率高达91.06%，与hinge作为损失函数的标准SVM相比，分类准确率提高了2.65%，同时高于线性分类的90.40%和逻辑回归的83.77%。依据此结果，本实验选择以Chinge为损失函数的C-SVM作为分类模型，在接下来的测试中结合其他模型进行训练和测试。

表3 不同模型的分类效果Table 3 Classification effect of different models

2.3.2 组级别的稀疏化方法比较

根据组稀疏范数的定义，在组级别的稀疏范数的分类模型中，由于组稀疏的约束作用，将倾向选择与AD分类相关性较大的部分脑部区域，使得选中的每个区域内的体素相对集中，从而更好地展示与AD疾病有关的大脑区域。为了验证组稀疏范数的分类效果，选取GL、GL1/2和SGL1/2 3种组稀疏范数进行对比。图6展示了基于AAL模板的GL和SGL1/2校准支持向量机模型在大脑区域选取的重要分类区域，其中λ2是用于控制组稀疏范数的超参数。可以看出，海马、海马旁回、舌回和梭状回等区域对于AD的分类非常重要，这些组方法基本上都选取了这些区域。不同的是，SGL1/2方法对选中区域内的一些体素进行了稀疏，去除了一些相关度较低的体素，选中的脑部区域如表4所示。图6(a)—(c)是C-SVM+SGL1/2模型，能够选取高相关脑区的高相关体素，在加大正则化项惩罚时，仅会去除相对相关度低的脑区和相关度高的脑区中相对相关度低的体素，因此红色标注区域会近似对称；图6(d)—(f)是C-SVM+Group Lasso(GL)模型，仅针对组间进行稀疏，一旦认为某些脑区相对较其他脑区相关性低时，将去除整个脑区中的所有体素。因此在加大正则化项惩罚时，会依次去除相对相关性低的完整脑区，导致惩罚较大时红色标注区域不完全对称的视觉效果。组级别范数的C-SVM在AD与CN上的分类性能如表5所示，图7是基于AAL模板的组方法模型的分类性能比较。结合表5和图7可以看出，以AAL为分组模板的SGL1/2校准支持向量机有一个更好的分类效果，平均运行时间最短，而GL1/2 + C-SVM平均运行时间最长，这是由于GL1/2的不稳定性引起的。GL的稀疏效果没有SGL1/2强，因此存在更慢的迭代求解速度。SGL1/2范数是对GL1/2的一种平滑逼近，二者的组稀疏效果大致相同，但是改进的平滑GL1/2范数SGL1/2能够使函数更快收敛，防止数据发生振荡。

图6 基于AAL模板分组的不同组稀疏模型选中的组特征区域Fig.6 AAL template grouping based group feature regions selected by different group sparsity models((a) SGL1/2 and λ2= 0.000 1; (b) SGL1/2 and λ2= 0.002; (c) SGL1/2 and λ2= 0.05; (d) GL and λ2= 0.001; (e) GL andλ2= 0.01; (f) GL and λ2= 0.1)

表4 基于SGL1/2的C-SVM模型(本文模型)在ADNI的数据集上选择的脑区Table 4 Selected brain regions of C-SVM model based on SGL1/2(proposed model) in ADNI dataset

表5 组级别范数的C-SVM在AD与CN上的分类性能Table 5 Classification performance of group level norm C-SVM on AD and CN

图7 基于AAL模板的组方法模型的分类性能比较Fig.7 Classification performance comparison of group method models based on AAL template

2.3.3 对较难分辨的对照组的分类效果测试

本文结果表明平滑稀疏化在组级别上是有效的，使得特征选择更加聚集，获取与疾病高度相关的局部区域，有更好的分类效果。前文比较了脑部形态差异最大的AD与CN组，在实际中，很多病患通常处在介于AD和CN之间的MCI状况，临床表现通常没有AD患者严重，这种状态与其他两种状态也更难进行区分，分类边界较为模糊。为了进一步验证模型性能，对AD 组与MCI组、CN组与MCI组进行分类测试，分组模板仍使用AAL模板，对比GL和SGL1/2两种组稀疏方法，结果如表6所示，表6中时间为平均求解时间。可以看出，在AD与MCI对照组中，SGL1/2模型的分类准确度为71.47%，高于GL模型的70.62%，平均运行时间较GL减少269.34 s，效率提升33.53%；在MCI与CN对照组中，SGL1/2模型准确率为78.81%，比GL模型高1.97%，时间效率比GL提高38.30%。

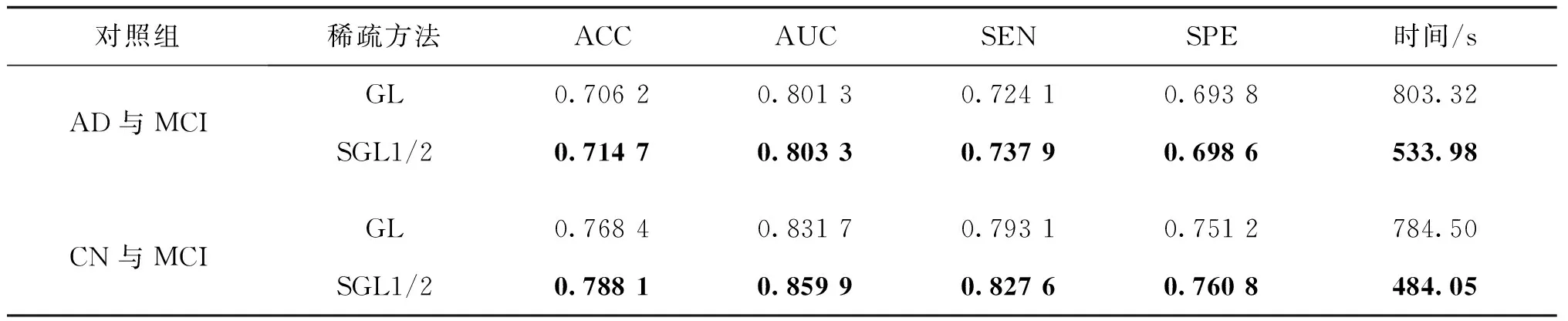
表6 基于SGL1/2的C-SVM模型在困难对照组上的分类结果Table 6 Classification performance of C-SVM model based on SGL1/2 in more difficult control group

AD与MCI、CN与MCI的分类效果分别如图8和图9所示。可以看出，基于SGL1/2范数的分类模型的分类性能都明显高于基于GL范数的分类模型。由此可见，基于SGL1/2的C-SVM模型在更困难的对照组中也能体现良好的分类效果，这对模型的可靠性是一个强有力的支持。

图8 基于SGL1/2的C-SVM模型在AD与MCI的分类效果Fig.8 Classification effect of C-SVM model based on SGL1/2 in AD and MCI

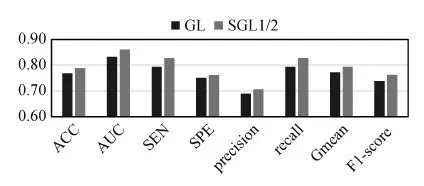
图9 基于SGL1/2的C-SVM模型在CN与MCI的分类效果Fig.9 Classification effect of C-SVM model based on SGL1/2 in CN and MCI

2.3.4 在Cuingnet数据集的分类性能

为了验证本文模型的泛化能力，使用Cuingnet数据集对本文模型进行训练和测试。根据不同疾病状态分为不同对照组，即CN与MCI、AD与MCI以及MCIc与MCIs。其中，MCI组由MCIc和MCIs合并而成。通过调整正则化项的超参数，在训练数据上进行重新优化，其他参数和其他模型一致，完成训练后再进行测试。本文模型与无稀疏操作和GL稀疏化两种方法的对比结果如表7所示，表7中时间为平均求解时间。可以看出，在所有对照组中，SGL1/2的分类性能在大部分情况都高于其他模型的分类性能，仅在CN与MCI组呈较为接近状态，求解时间均大幅降低，在AD与MCI组和CN与MCI组中，在保持高于或近乎持平的分类性能前提下，时间效率较GL方法提升了近60%，优势明显。同时，基于组范数的C-SVM的各项分类性能都优于无范数的C-SVM模型，同时SGL1/2略优于GL，基于SGL1/2的C-SVM模型在Cuingnet数据集上也能相较于其他正则化范数达到更好的效果，这充分说明了该模型应对其他数据集时具有较强的泛化能力。

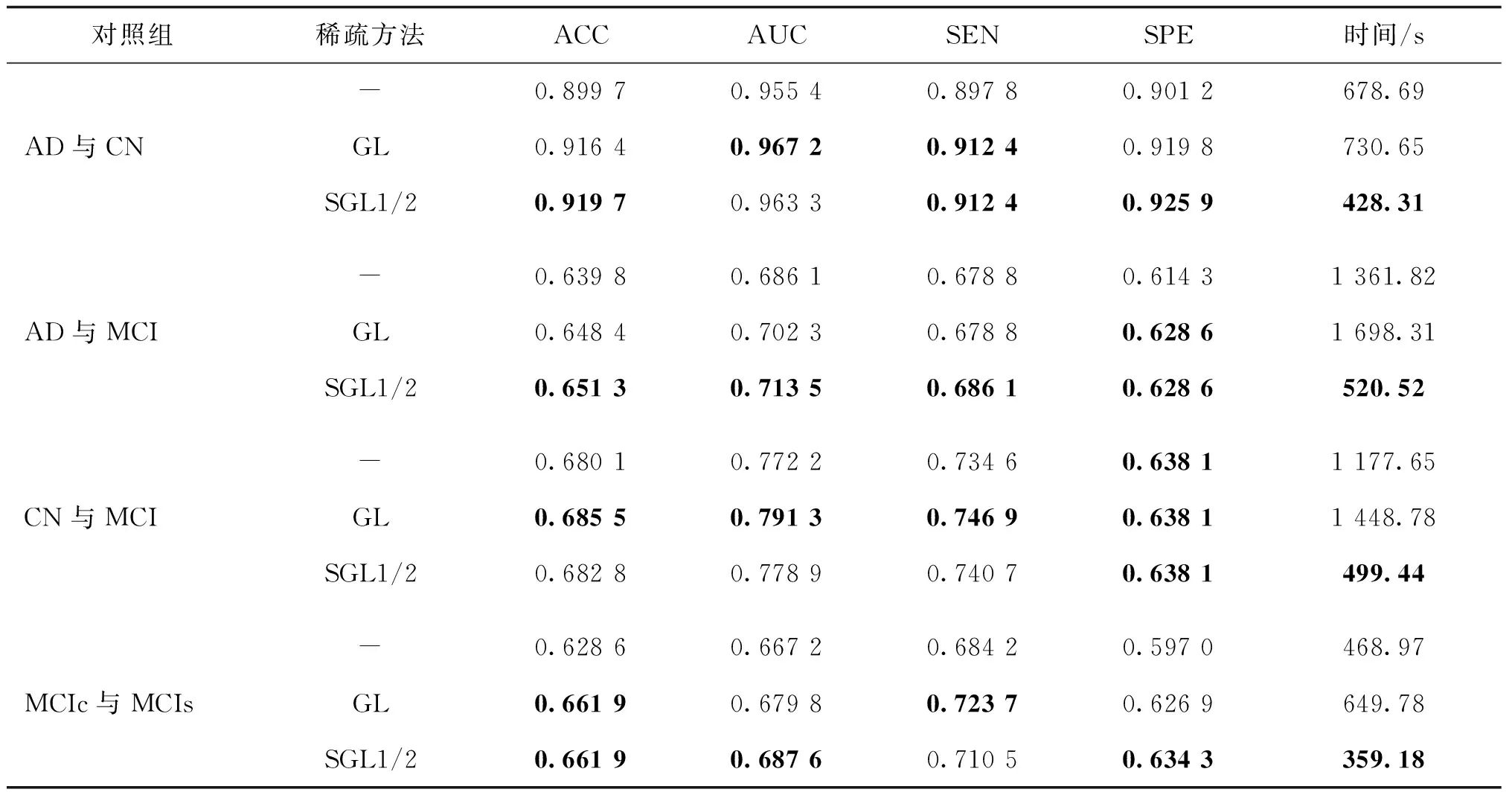
表7 基于SGL1/2的C-SVM模型在Cuingnet数据集上的分类性能Table 7 Classification performance of C-SVM model based on SGL1/2 on Cuingnet dataset

3 基于AAL模板的各特征组独立分类效果比较

为进一步了解与AD高度相关的单独脑部区域对区分AD的效果，以AAL分组模板对进行分组的各组特征使用单独分类函数进行分类，对左右脑平均分类排名前27的脑部各区域及同一区域左右脑区的分类效果进行对比，结果如图10所示。其中，分类效果最好的右舌回(Lingual_R)、右海马旁回(ParaHippocampal_R)、右海马(Hippocampus_R)、右梭状回(Fusiform_R)、左颞下回(Temporal_Inf_L)和左背外侧额上回(Frontal_Sup_L)6个脑区的具体分类效果如图11所示。

图10 单独分类模型在AAL模板中左右脑区域分类准确率比较Fig.10 Comparison of classification accuracy between left and right brain in AAL template

将高相关的单独组区域得到的最佳结果与基于SGL1/2正则化的C-SVM模型进行比较，如表4和图11所示，可以发现这种组稀疏方法也基本选中了本文模型获取的分类准确率排名前6的脑区，证明了该组方法的可靠性。同时，本文模型在基于AAL模板中获得的分类准确度为94.70%，比高相关单独组经过非组稀疏的最佳分类准确率高2.32%，这一结果同样很好地证明了多个脑区之间存在一定的相关性，它们共同影响AD的发病。

图11 分类准确率排名前6的脑区Fig.11 Brain regions with top 6 classification accuracy

4 与现有方法比较

为了进一步验证本文基于SGL1/2组稀疏方法的C-SVM分类模型性能优越性，与多核学习方法(multiple kernel learning，MKL)(Ben Ahmed等，2017)、3维卷积神经网络(3D convolutional neural networks，3D-CNN)(khvostikov等，2018)、SVM+GL+SAR(spatial anatomical regularization)(Sun等，2018)、deep CNNs(convolutional neural networks)(Aderghal等，2018)、3维卷积神经网络与长短期记忆网络(3D convolutional neural networks—long short-term memory，C3d-LSTM)(Li等，2020)和SVM+ROICSE(ROI-based contourlet subband energy(Feng等，2021)等AD诊断方法在ADNI数据库上进行对比，以诊断准确率(ACC)为评判指标，结果如表8所示。可以看出，本文模型具有更好的分类效果。

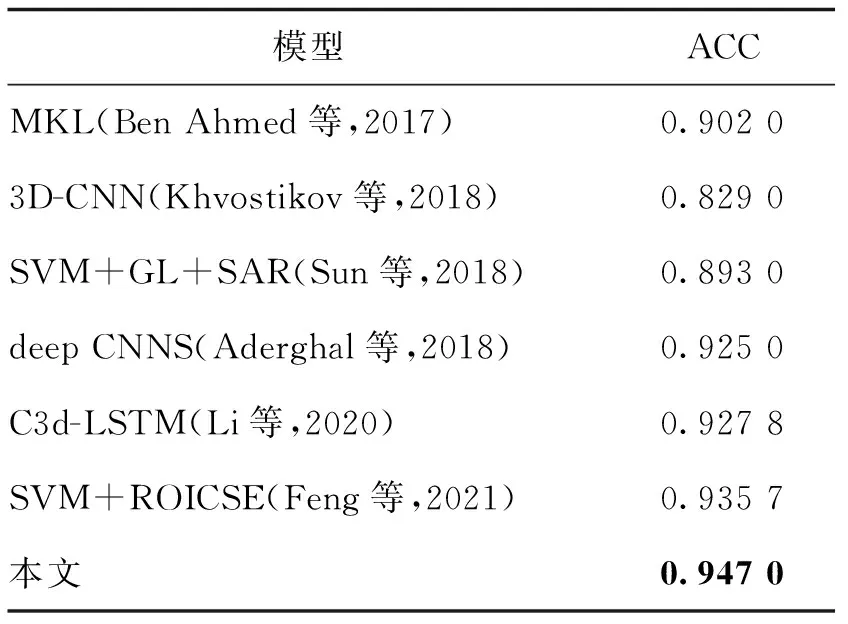
表8 不同方法分类性能比较Table 8 Comparison of classification performance of different methods

5 结 论

本研究提出基于解剖平滑分组的L1/2正则化方法，并结合校准支持向量机组合成分类框架，实现对阿尔茨海默症(AD)的分类。这种平滑解剖分组稀疏的方法以流行的Group Lasso为原型，针对性地解决了Group Lasso不能对每个解剖组内的特征进行稀疏的缺点，达到可以同时去除冗余组和相关组内一些冗余特征的效果。此外，针对组级别上的正则化范数提出了经过配准后的AAL模板，将每个区域作为一组，每个区域内所有体素作为每组的特征进行组稀疏。然后在提出的C-SVM框架中以组为级别进行训练，最后预测出受试者是否患有AD。实验结果表明，本文模型结果比其他稀疏范数有更好的结果，分类准确率最高达94.70%。同时，选中的权重分布较为集中，能够更好地发现与疾病高度相关的区域，增强了可解释性。根据权重图的分布情况可以将选定脑部区定位到AD相关的脑部区域，并且选择的区域也会较为集中。根据当前的知识可知，海马旁回、舌回和梭状回是与AD高度相关区域，权重图在这些区域也展现了较高的相关性，这为实验结果的合理性提供了有效支持。