微观等效毛管束下液体初始渗流特性的可视化研究

王 刚，李艳青，刘世民，李怀兴，商荦真，陈 建

（1.山东科技大学矿山灾害预防控制省部共建国家重点实验室培育基地，山东 青岛 266590；2.山东科技大学安全与环境工程学院，山东青岛 266590；3.宾夕法尼亚州立大学地球与矿物科学学院，宾夕 法尼亚州斯泰特科利奇 16802）

0 引 言

煤层注水是煤矿降尘防突的重要技术措施之一［1-3］。 煤作为一种孔裂隙发达的多孔介质，宏观尺度下液体在煤中的运移过程和规律已被广泛研究。 但低渗透储层中存在着大量的微纳米孔隙和孔喉，基于宏观尺度的Darcy 渗流定律已不能完全适用［4］。 因此，研究微观尺度下煤体孔隙特征，确定微观孔隙液体渗流机理，具有十分重要的科研价值和现实意义。

微尺度是一个相对的概念，在不同的场合和领域有着不同的定义。 一般认为特征尺度为0.1 ～10 μm 时可以称为微尺度［5-7］。 目前，微尺度下的孔裂隙中液体渗流研究仍停留在模拟层面。 综合国内外研究学者对煤体孔隙模型重构及模拟渗流过程，大致可以分为2 类，一类是基于CT 扫描后所获得图像进行处理并建模。 孟祥曦［8］对煤块进行CT 扫描后，构建了煤体骨架模型，利用COMSOL 模拟软件探究了渗流水的运动规律。 笔者团队［4，9-10］运用CT扫描和三维重建技术建立了含有孔裂隙的三维煤体骨架结构模型，进行了煤层内水和气的渗流模拟研究。 KARIMPOULI［11］将微型CT 扫描所建模型和考虑裂隙非均质性的离散裂隙网络模型进行对比，研究了不同模型下的渗透率。 一类是基于建模后的煤孔裂隙结构进行数值模拟研究。 朱斌等［12］建立了裂隙-孔隙双重介质模型，研究了时间和空间上的孔隙水压变化过程。 JING［13］建立了一种裂缝-微孔混合网络模型（FM-PNM），研究了压裂煤中瓦斯随时间的变化过程。 张渤［14］建立了煤层瓦斯运移的流-固耦合数学模型，研究了裂隙结构特征对煤岩渗透性的影响。 尽管微观尺度液体渗流研究已取得了一定成果，但从试验角度进行液体渗流过程的可视化研究仍较为空白。

随着微流控技术的发展，微观尺度下的液体渗流可视化试验研究似乎有望得到突破。 微流控技术是专门用于研究微尺度范围流体间相互作用的技术，对研究微观结构内复杂流体的渗流规律具有很好的适用性，微流控芯片良好的透光性能使渗流过程易于实现可视化［15-16］。 国内已有很多学者利用微流控技术促进了流体渗流机理的深入研究。 李登伟等［17］利用激光刻蚀技术制备了均质微观孔隙模型，开展了低渗透油气藏岩心气水两相渗流试验。钱自卫等［18］以真实砂岩为基础，制备了透明微细孔隙试验模型，利用微流控技术研究了微观尺度松散砂层内流体非线性渗流的机理。

上述研究表明，煤体微尺度下流体渗流规律具有重要意义已经成为共识，但是受到仪器材料和检测手段等限制，低渗煤层微尺度下液体渗流规律仍未明晰。 微流控技术能够精确控制和操控微尺度流体，清晰直观地观察到流体的渗流特性，是一种很有发展前景的研究手段。 因此，本文以微流控技术为基础，制作可替代煤体孔隙的毛管束模型，构建了微观渗流可视化试验平台，进行了微观尺度下等效毛管束模型中液体初始渗流特性的可视化试验研究，进一步揭示煤体微观渗流特性。

1 毛管束模型定义与制备

1.1 毛管束模型的定义

根据储层多孔介质的性质建立相应的物理模型是常用的研究手段之一，其中最常用的经典模型为毛管束渗流模型［19-20］。 为了数学上的简便计算和更加形象地表征多孔介质的孔隙空间，选用等径的毛管束模型代替煤体孔隙空间来研究流体渗流。

1.2 透明毛管束模型制备

孔隙模型为达到微小孔隙管道的要求，采用光刻技术，能比较精准地实现微小通道的制备，降低误差。 制作模型时首要考虑的是材料具有透明性，便于观察微尺度下流体的渗流状态。 其次，在微观尺度下，微观力起主导作用，而表面力对微观力有着极其重要的影响，在选择材料时应充分考虑润湿性的影响。 最后，材料应具有良好的稳定性，能够被刻蚀成一定的形状。 因此，充分考虑各种因素的影响后，选择无毒无害且与硅片之间有良好黏附性的聚二甲基硅氧烷（PDMS）作为物理模型的材料。

物理模型如图1 所示，孔隙模型外观为T 型，厚度为2 mm，包括孔隙结构体、缓冲舱和出入口。 孔隙结构体为长方体状，长为1.1 mm，宽为0.3 mm；缓冲舱分列于孔隙结构体两侧，为梯形状，上边长为0.09 mm，下边长为0.6 mm；出入口为圆管状，直径为0.09 mm。 根据毛管束孔隙半径分布概率［5］，孔隙通道直径分别刻蚀为4、7、10 μm，通道数目皆为100，等距均匀分布。

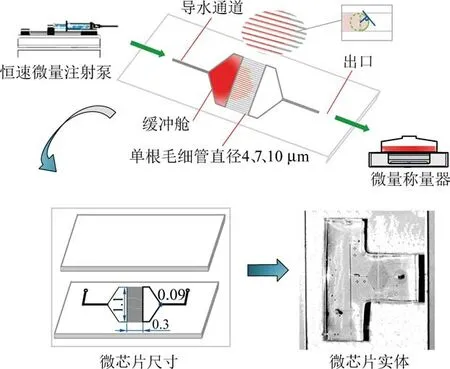
图1 透明毛管束微孔隙模型Fig.1 Transparent capillary bundle micropore model

1.3 模型可行性验证

液体的润湿性或润湿能力与两相流系统的组分构成和接触壁面有直接关系，接触角是润湿程度的主要度量，为探究毛管束模型能否等效真实环境下的煤层微孔隙，分别测试毛管束模型和煤样压片的接触角，结果如图2 所示。 毛管束模型的接触角为78°，煤样压片的接触角为71°，误差小于10%，在误差允许范围内。

图2 煤样与模型接触角测量Fig.2 Measurement diagram of contact angle between coal sample and model

此外，通过拉伸试验机分别在室温下对纯PDMS 基体和渝阳煤矿的无烟煤型煤进行准静态单向拉伸试验。 试验控制加载速率为5 mm／min，每个样品测量5 次取平均值。 纯基体与型煤的拉伸应力-应变曲线如图3 所示。 从图3 可以看出，纯PDMS 基体的应力应变与型煤煤样的变化趋势具有一定相似性。

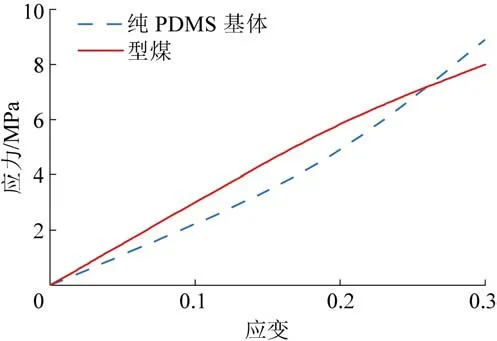
图3 纯PDMS 基体和型煤的应力应变曲线Fig.3 Stress-strain curve of pure PDMS matrix and briquette

对比分析PDMS 与煤的润湿性及力学性能，可以得知二者在界面力学与宏观力学上具有一定的相似性。 因此可以选择毛管束模型作为煤层微孔隙的代替品进行微观尺度下的流体渗流研究。

2 渗流试验平台及试验方案

2.1 试验平台

为研究微尺度下煤层孔隙流体流动特性，构建了如图4 所示的微观渗流可视化试验平台，包括注液系统、压力监控系统、模拟孔隙模型、可视化观测与数据采集系统和连接各系统的管阀件5 部分。 压力驱动系统主要由实验室注水泵、注射器以及管阀件组成，其主体为实验室TYD01 型注水泵，可以对其进行注水流量设置。 压力监控系统由液体压力传感器、Sensor Reader 传感器数据采集卡和ElveflowⒸSmart Interface 智能采集软件组成，测量范围为0～689.5 kPa。 微流体压力传感器可以监测各种微流体产生的压力，通过数据采集卡获取数据，在ESI中记录和输出所有压力传感器产生的压力数据。 可视化观测与数据采集系统主要是由光学电子显微镜和电脑组成，显微镜型号为Leica DVM 2500，可以实时观察反应过程中微液体的状态变化。

2.2 试验方案

试验时模型水平放置，采用多参量对比分析法进行试验。 试验时先连接好微观渗流可视化平台各个设备，再通过调节液体注入流量来观察压力梯度的变化。 流量变化范围根据试验要求可自主设置，流量变化梯度为1 μL／min，注水压力采集频率为1 次／s，具体参数见表1。 不同孔径测量时步骤相同。 为更好地在显微镜下观察流体渗流过程，将流体处理成显色度更好的红色，在显微镜下观察流体的渗流过程。

表1 模型试验条件Table 1 Experimental conditions of the model

正式试验前先开展管路同等流量梯度的注水渗流试验，获取注水压力值平均值。 孔隙模型渗流压力为注水压力减去管路渗流压力，孔隙模型渗流流量为注入流量减去管路渗流流量，后文如无特殊说明，压力表示孔隙模型渗流压力，流量表示孔隙模型渗流流量。 为保证试验结果的准确性，分别进行3次平行试验取平均值。

3 渗流试验结果分析

3.1 渗流过程分析

根据等效毛管束模型的定义，微尺度下的液体孔隙渗流呈现一定的规律，以下简称微流动。 设置梯度变化的渗流初始流量，在流体到达缓冲区域时停止注射泵，静置10 min，观察渗流过程。 待渗流完全停止后，通过光学数码显微镜观察参与渗流的孔道数目，获取图片并使用图像处理软件计算实际渗流孔隙体积，然后得到孔隙模型内初始流量与参与渗流通道数目及渗流体积占比的关系曲线。

图5 为渗流初始流量为1 μL／min 的去离子水在直径为10 μm 的孔隙模型中孔隙渗流过程观测图。 32 s 时流体到达缓冲区域，停止注射泵后，流体在缓冲区域内先是混合流动，然后逐渐变为层流，渗流到毛细管内。 12 min 左右渗流几乎停止，图5 最下方2 个图为渗流过程停止时中间区域的渗流情况。 从图5 可以看出，不同位置渗流活跃性差异较大，比如中间位置渗流时流体动能较大，渗流发生较早；两边位置渗流时流体动能已降低或消失，无法渗流至毛细管中。

图5 孔隙渗流过程观测Fig.5 Observation of pore seepage process

进一步探究发现，随着初始流量梯度的增加，在卸载压力后，参与渗流的孔隙通道数逐渐增加，毛细管内渗流的孔隙体积增加，呈线性增长趋势，如图6所示。 自发渗流过程中，初始流量越大，流体流速越大，根据力学平衡方程，能够克服启动压力梯度的毛管数也越多［20-21］；同时，随着初始流量梯度的增加，渗流通道增加的速度逐渐小于渗流体积的增加速度，说明在微观孔隙中，流体克服毛细管力渗流的速度小于在管内的渗流速度。

图6 孔隙渗流实验监测数据Fig.6 Experimental monitoring data of pore seepage

3.2 渗流压力对微流动的影响

图7 为渗流流量为1～4 μL／min 的去离子水在直径为10 μm 的孔隙模型中渗流压力梯度与流量曲线关系图。 从图7 中可以看出，在一个恒定流速下，渗流压力随时间增加增大；当流量为1 μL／min时，390 s 内压力达到了近5×104Pa，流量为4 μL／min 时，390 s 内压力达到了8×104Pa，表明流量越大，体系渗流压力越大。 压力和流量变化关系与流动理论较为符合，说明在宏观方面上去离子水与压力的关系符合Hagen-Poiseuille 流动规律。

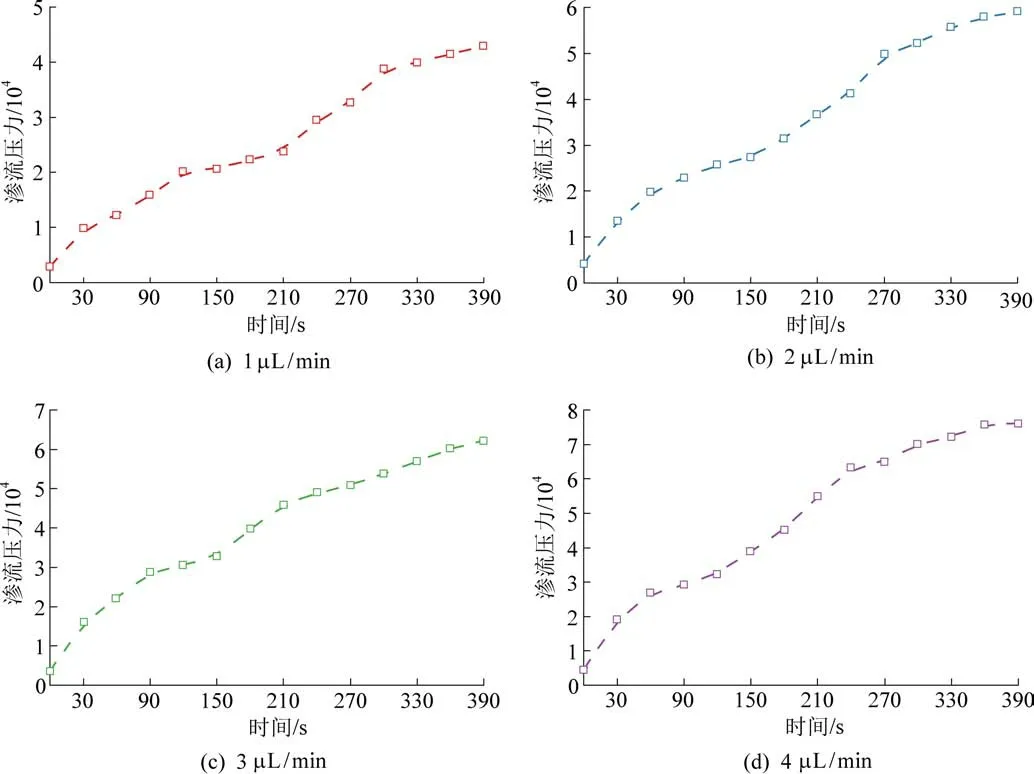
图7 渗流压力与流量曲线关系Fig.7 Relationship between seepage pressure and flow curve

微观角度上，在试验设置流量下，压力随时间先快速增长，然后出现一个较为平缓的阶段，紧接着又快速升高。 产生该现象可能是因为，去离子水要进入毛细管内，首先要克服毛细管内壁面流体层相对于壁面的摩擦力，由于流体应力应变的关系，去离子水发生弹性形变而产生的弹性势能逐渐积累，直至达到壁面流体层克服毛细管内壁面所需要的最大摩擦力，这一阶段表现为压力不断上升。当毛管束模型中去离子水第一次通过毛细管时，通过毛细管的去离子水恢复形变，出现泄压效应，这一阶段对应压力增长较为平缓阶段。 随着首端的去离子水的弹性形变持续发生，后续流动阶段的去离子水压缩性较小，应力应变不是线性关系，很小的弹性形变产生较大的弹性应力，因此压力时间曲线在平缓上升依旧会以斜率增大的形式继续迅速攀升［22-23］。

3.3 孔径尺度对微流动的影响

3 种孔径尺度的毛管束模型中去离子水的平均流量与压力关系如图8 所示。 从图中可以看出，在孔径尺度小于或等于10 μm 时，渗流压力与流量相对趋势不变，但3 种尺度下压力和流量都呈现出不同程度的非线性特征，且孔径尺度越小，非线性程度越强。

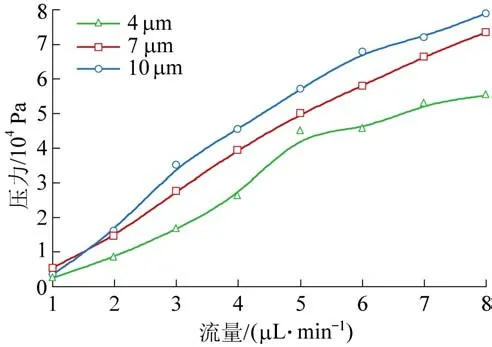
图8 渗流压力与孔径尺度关系Fig.8 Relationship between seepage pressure and pore size

究其原因，主要是由于微米尺度下，体积力的作用下降，流体分子间作用力以及固体表面与流体分子间作用力的作用上升。 黏性力的作用增强，惯性力降低，且越靠近毛细管壁面这种作用规律越明显。此外，毛细管中面积与体积比都增大，与微管道表面积呈比例的表面力可能成为主导力，此时Hagen-Poiseuille 方程不再完全适用，流体流动有向非线性转变的特征，且微管半径越小，非线性特征越明显，说明半径越小，分子间作用力对微尺度流动影响越大［24］。

3.4 润湿性对微流动的影响

流体在煤体中的渗流其实是其在若干不同量级的孔隙中流动的宏观表现，润湿性对孔隙中微流动的影响将导致煤体渗流特性的变化。 使用20 ℃下表面张力为16 mN／m 的增渗流体（低表面张力纳米流体）和去离子水（72 mN／m）进行对比试验，得到图9 所示结果。

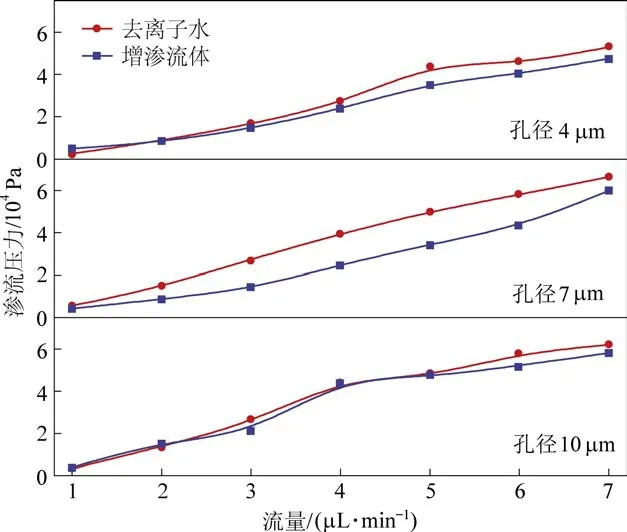
图9 渗流压力梯度与润湿性关系Fig.9 Relationship between seepage pressure gradient and wettability

由图9 可知，在小于10 μm 的微尺度下，增渗溶液表面张力低，流体对壁面的润湿性更好，渗流压力整体更小。 这是由于煤层对去离子水具有吸附作用力，边界附近的流体吸附在毛细管内壁上，形成吸附水膜不参与流动，表面张力越大水膜厚度越大，这种水膜在流动中表现为流动阻力［25］，在宏观尺度下这种水膜可以忽略不计，但在微尺度下，固液相互作用力放大，水膜带来的阻力作用凸显，因此，表面张力越大水膜越厚，流体流动阻力变大，通过毛细管时的渗流压力也变大。

从图9 还可以看出，表面张力的影响随着流量增加效果增强。 在流量较小时，不同孔径下去离子水和增渗溶液的渗流压力十分接近，随着流量增加，低表面张力流体渗流压力更小。

4 结论与展望

1）微观尺度下等效毛管束模型可视化试验过程中不同位置的渗流活跃度不同；中间区域的渗流活跃度大于边缘区域渗流活跃度；渗流初始流量与参与渗流通道数目及毛细管内渗流体积占比成正比。

2）渗流流量不变时，渗流压力和时间呈正相关，随着渗流流量增加，体系渗流压力增大；毛管束内渗流速率波动变化，存在非线性渗流特征。

3）不同孔径尺度下压力和流量相对关系基本不变，呈正比关系；3 种尺度的模型中流量和压力都呈现非线性特征，且孔径越小，非线性程度越强烈。

4）相同流量下，表面张力较低的增渗液体产生的渗流压力更小；不同孔径下，流量值的大小与不同液体渗流压差成正比，即流量值较大时，表面张力不同的液体渗流压力差距也会逐渐增大。

由于时间和条件限制，本文研究内容仍较为有限，后续将进一步进行稳态渗流研究及尝试构建考虑迂曲度和粗糙度的物理模型。